广东省珠海市广东实验中学金湾学校2022-2023学年高二下学期数学素养测试题1

2022学年珠海市广东实验中学金湾学校高二数学素养测试题1

测试时间：40分钟  考查内容：形数

班级：___________姓名：___________分数：___________

一、单选题（每道题5分，共15分）

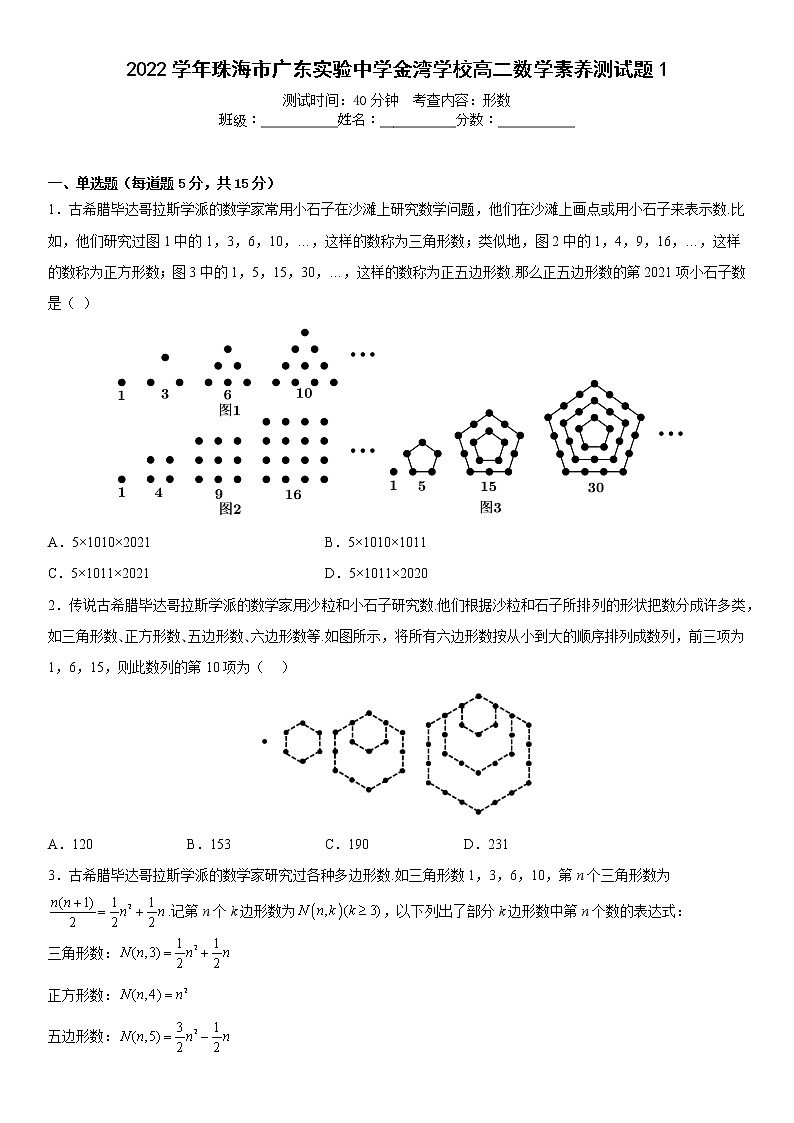
1．古希腊毕达哥拉斯学派的数学家常用小石子在沙滩上研究数学问题，他们在沙滩上画点或用小石子来表示数.比如，他们研究过图1中的1，3，6，10，…，这样的数称为三角形数；类似地，图2中的1，4，9，16，…，这样的数称为正方形数；图3中的1，5，15，30，…，这样的数称为正五边形数.那么正五边形数的第2021项小石子数是（ ）

A．5×1010×2021 B．5×1010×1011

C．5×1011×2021 D．5×1011×2020

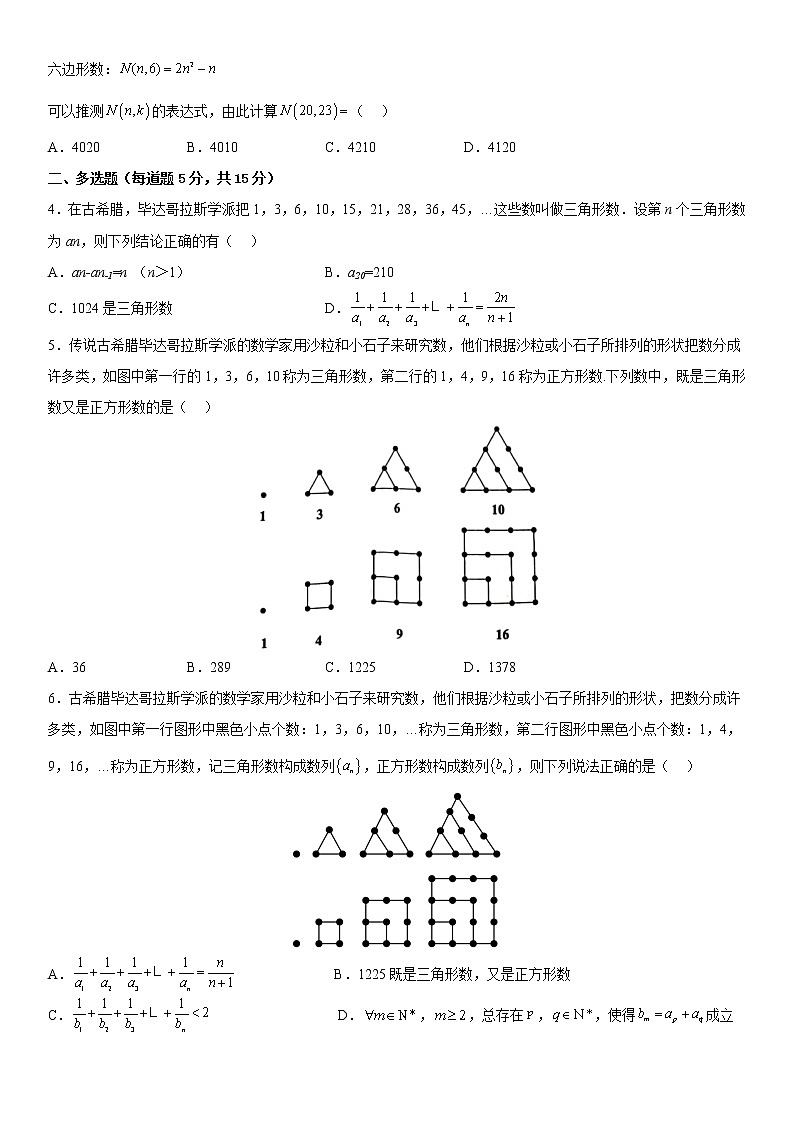
2．传说古希腊毕达哥拉斯学派的数学家用沙粒和小石子研究数.他们根据沙粒和石子所排列的形状把数分成许多类，如三角形数､正方形数､五边形数､六边形数等.如图所示，将所有六边形数按从小到大的顺序排列成数列，前三项为1，6，15，则此数列的第10项为（    ）

A．120 B．153 C．190 D．231

3．古希腊毕达哥拉斯学派的数学家研究过各种多边形数.如三角形数1，3，6，10，第n个三角形数为.记第n个k边形数为，以下列出了部分k边形数中第n个数的表达式：

三角形数：

正方形数：

五边形数：

六边形数：

可以推测的表达式，由此计算（    ）

A．4020 B．4010 C．4210 D．4120

二、多选题（每道题5分，共15分）

4．在古希腊，毕达哥拉斯学派把1，3，6，10，15，21，28，36，45，…这些数叫做三角形数．设第n个三角形数为an，则下列结论正确的有（    ）

A．an-an-1=n （n＞1） B．a20=210

C．1024是三角形数 D．

5．传说古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数，他们根据沙粒或小石子所排列的形状把数分成许多类，如图中第一行的1，3，6，10称为三角形数，第二行的1，4，9，16称为正方形数.下列数中，既是三角形数又是正方形数的是（    ）

A．36 B．289 C．1225 D．1378

6．古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数，他们根据沙粒或小石子所排列的形状，把数分成许多类，如图中第一行图形中黑色小点个数：1，3，6，10，…称为三角形数，第二行图形中黑色小点个数：1，4，9，16，…称为正方形数，记三角形数构成数列，正方形数构成数列，则下列说法正确的是（    ）

A．              B．1225既是三角形数，又是正方形数

C．                  D．，，总存在，，使得成立

三、填空题（每道题5分，共30分）

7．把1，3，6，10，15，…这些数叫做三角形数，这是因为这些数目的圆点可以依次排成如图所示的相应边长的正三角形（其中，假定1个圆点排成的正三角形的边长为0），则第100个三角形数是______．

8．传说古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数．用一点（或一个小石子）代表1，两点（或两个小石子）代表2，三点（或三个小石子）代表3，…他们研究了各种平面数（包括三角形数、正方形数、长方形数、五边形数、六边形数等等）和立体数（包括立方数、棱锥数等等）．如前四个四棱锥数为第n个四棱锥数为1+4+9+…+n2＝．中国古代也有类似的研究，如图的形状出现在南宋数学家杨辉所著的《详解九章算法•商功》中，后人称为“三角垛”．“三角垛”的最上层有1个球，第二层有3个球，第三层有6个球，…若一个“三角垛”共有20层，则第6层有 ____个球，这个“三角垛”共有______个球．

9．传说古希腊毕达哥拉斯学派的数学家常用小石子来研究数．他们根据小石子所排列的形状把数分成许多类，如图（1）可得到三角形数1，3，6，10，…，图（2）可得到四边形数1，4，9，16，…，图（3）可得到五边形数1，5，12，22，…，图（4）可得到六边形数1，6，15，28，…．进一步可得，六边形数的通项公式______，前n项和______．

（参考公式：）

10．古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数，他们根据沙粒或小石子所排列的形状，把数分成许多类，如图，第一行图形中黑色小点个数：1，3，6，10，…称为三角形数，第二行图形中黑色小点个数：1，4，9，16，…称为正方形数，记三角形数构成数列，正方形数构成数列，则______；______.

11．传说古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数他们根据沙粒或小石子所排列的形状把数分成许多类，下图中第一组的1，3，6，10称为三角形数，第二组的1，5，12，22称为五边形数，则三角形数的第7项为___________，五边形数的第n项为___________.

答题卡

填空题

8.             ；           

9.             ；           

10.            ；           

11.            ；           

2022学年珠海市广东实验中学金湾学校高二数学素养测试题1

参考答案

1．A

【分析】设正五边形数构成数列，根据题中条件，得到递推关系，再由累加法，即可得出通项公式，从而可求出结果.

【解】设正五边形数构成数列，则，，且当时，，

于是，

故.

故选：A.

2．C

【分析】由题意归纳推理出通式，即可得到第10项.

【解】由题意可知，，，，

故总结，由第四个图知，，满足通式，

故.

故选：C.

3．B

【分析】由，即可归纳出的表达式，即可求值.

【解】，

，

，

.

由此可归纳，

所以.

故选：B

4．ABD

【分析】通过归纳可判断A；通过累加可判断B；通过解方程可判断C；通过裂项相加可判断D.

【解】∵，，，…，

由此可归纳得，故A正确；

将前面的所有项累加可得，∴，故B正确；

令，此方程没有正整数解，故C错误；

，故D正确.

故选：ABD.

5．AC

【分析】由题意，整理数列的通项公式，建立方程，可得答案.

【解】由题意，三角形数可看作，，，，

则第三角形数为；

正方形数可看作，，，，，则第个正方形数为；

对于A，令，解得，令，解得，故A正确；

对于B，令，解得，令，其解显然不是正整数，故B错误；

对于C，令，解得，令，解得，故C正确；

对于D，令，显然其解布置正整数，故D错误.

故选：AC.

6．BCD

【分析】根据给定信息，求出数列、的通项，再逐一分析各个选项即可判断作答.

【解】依题意，数列中，，，，

于是得，满足上式，

数列中，，，，

于是得，满足上式，

因此，

对于A，，则，A不正确；

对于B，因为，则，又，则，B正确；

对于C，，

则，C正确；

对于D，，，取，则，

所以，，总存在，，使得成立，D正确.

故选：BCD

7．5050

【分析】观察图像规律，1是第一个三角形数，3是第二个三角形数，6是第三个三角形数，依此类推，第100个三角形数是1到100连续自然数的和，相加即可.

【解】观察图像规律发现，三角形数是从1开始的连续自然数的和，1是第一个三角形数，3是第二个三角形数，6是第三个三角形数，10是第四个三角形数，15是第五个三角形数，，所以第100个三角形数是：，故第100个三角形数是5050.

故答案为：5050

8．     21     1540

【分析】根据题中给出的图形，结合题意找到各层球的数列与层数的关系，得到＝，由此可求的值，以及前20层的总球数．

【解】由题意可知，

，

故＝＝，

所＝＝21，

所以S20＝a1+a2+a3+a4+⋯⋯+a20＝（12+22+32+⋯⋯+202）+（1+2+3+⋯⋯+20）

＝×+×＝1540．

故答案为：21；1540．

9．     ；     .

【分析】由题设易知是首项为5，公差为4的等差数列，累加法求通项公式，利用分组求和求.

【解】设六边形中，则是首项为5，公差为4的等差数列，

∴，

∴

，

∴，当时，符合该式，

∴，

.

故答案为：，.

10．     55    

【分析】首先观察三角形数，利用累加法求得，进而求出；利用正方形数得出，再利用裂项相消法求出即可求解.

【解】根据三角形数可知，，则，…，，

累加得，

，经检验也满足上式，故，

则；

根据正方形数可知，

当时，，

则

.

故答案为：；.

11．     28    

【分析】根据其图形规律得出其通项，即可得出答案.

【解】三角形数的每一项是从1开始的连续自然数的和，则，

则三角形数的第7项为，

五边形数的第一项为，第二项为，第三项为，

则五边形数的第n项为，

故答案为：28，.