2023届高三寒假数学二轮微专题45讲 08.双变量导数中的剪刀模型

 利用剪刀模型估计双变量

    双变量导数中的剪刀模型起源于2015年天津卷，在2021年新高考1卷中名满天下！该模型的实质是凸凹函数切割线放缩（牛顿切线法），值得注意的是，该方法已经出现在人教版新教材选择性必修二82页阅读材料中，未来完全可能再度出现在高考试题中！本节我们就通过这两道高考题展示其基本原理与解题方法.

一．基本原理

1. 函数凸凹性：

若函数在区间上有定义，若，则称为区间上的凸函数. 反之，称为区间上的凹函数.

2. 切线不等式： 在上为凸函数，，有. 反之，若为区间上的凹函数，则，有.

证明：取定，令，则，再次求导可得. 故在区间上递减，在区间上递增，故存在最小值，即，即证毕.

注：切线不等式是剪刀模型的理论依据.

3.剪刀模型

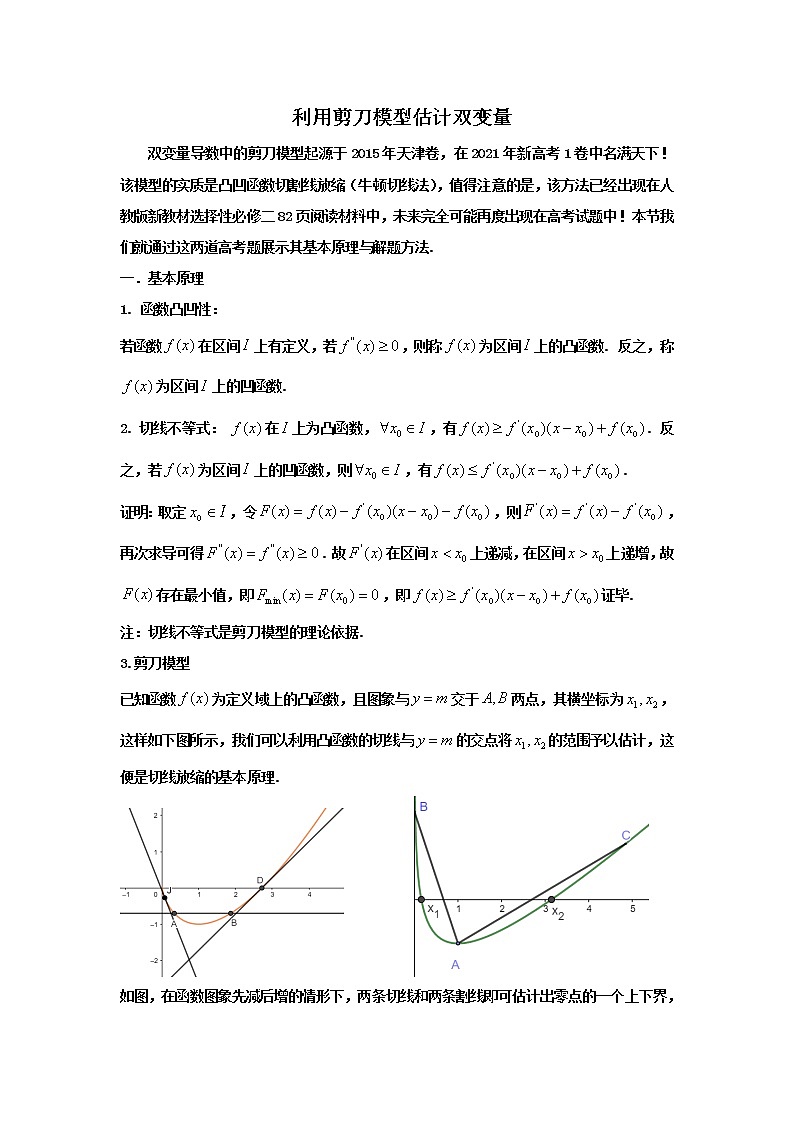
已知函数为定义域上的凸函数，且图象与交于两点，其横坐标为，这样如下图所示，我们可以利用凸函数的切线与的交点将的范围予以估计，这便是切线放缩的基本原理.

如图，在函数图象先减后增的情形下，两条切线和两条割线即可估计出零点的一个上下界，而切割线的方程均为一次函数，这样我们就可以得到一个显式解（精确解）的估计，下面我们通过例子予以分析.

二．应用分析

例1.（2021新课标1卷22题）已知函数.

（1）讨论的单调性；

（2）设为两个不相等的正数，且，证明：.

解析：注意到函数不含参数，那就求导分析凸凹性.，再求,,,在其定义域上分别是凹函数与凸函数.另一方面，，即，若令，则原命题等价于，已知证明：.

证明③.由于，不妨假设这是函数假设的图象与直线的两个交点，考虑到的图象性质可知.故而，即为方程的两根，结合函数的凸凹性，我们使用切线放缩来证明③.观察③的结构及可得在点处切线为.由前文背景理论常用性质（2）可知：.如图所示，假设与，交于两点，其横坐标为.与切线交于点，其横坐标.由图1可知：

.显然，再做函数图象的割线：，则显然：由图象可知：，，故.证毕.

例2.（2020合肥模考）已知函数(为自然对数的底数).

（1）求函数的零点，以及曲线在处的切线方程；

（2）设方程()有两个实数根，，求证：.

解：（1）曲线在处的切线方程为.曲线在处的切线方程为.

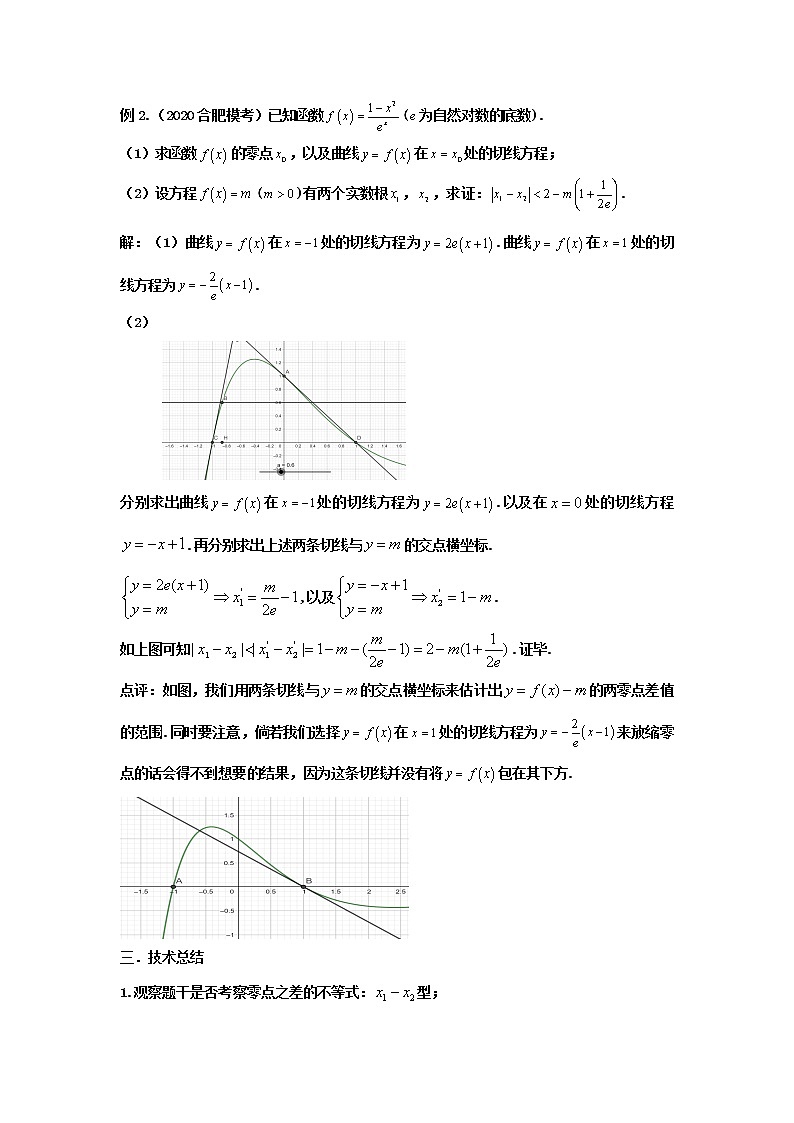
（2）

分别求出曲线在处的切线方程为.以及在处的切线方程.再分别求出上述两条切线与的交点横坐标.

,以及.

如上图可知.证毕.

点评：如图，我们用两条切线与的交点横坐标来估计出的两零点差值的范围.同时要注意，倘若我们选择在处的切线方程为来放缩零点的话会得不到想要的结果，因为这条切线并没有将包在其下方.

三．技术总结

1.观察题干是否考察零点之差的不等式：型；

2.验证函数的凸凹性；

3.在步骤2的基础上考察函数在关键特殊点处的切线，最终构造出剪刀模型，完成证明.

四．练习题

习题1．已知函数在点处的切线方程为.

（1）求；

（2）设曲线与轴负半轴的交点为点，曲线在点处的切线方程为，求证：对于任意的实数，都有；

（3）若关于的方程有两个实数根，，且，证明：.

习题2．设函数．

（1）求曲线在点处的切线方程；

（2）若关于的方程有两个实根，设为，（），证明：．

习题1.解：；. . 设的根为，则.曲线在点处的切线方程为，有，设的根为，则.

由于.又，所以.

习题2.解：（1）由于，又，,故在点的切线斜率，因此所求切线方程，即．

（2）由于，故时，，单调递减，

时，，单调递增，

由图易知，，，由（1）可知，在点的切线方程为，设与的交点横坐标为，且

即，下证．由于在单调递减，故只需证明即可．设（）．，故，，函数单调递减，

，，函数单调递增，因此，

即．又在处的切线方程为，设与的交点横坐标为，，即，下证．由于在单调递增，故只需证明即可，设，

，函数在单调递减，，

即．综上易知，，即．