2022-2023 数学京改版新中考精讲精练 中考模拟卷（一）

这是一份2022-2023 数学京改版新中考精讲精练 中考模拟卷（一），文件包含2022-2023数学京改版新中考精讲精练中考模拟卷一解析版docx、2022-2023数学京改版新中考精讲精练中考模拟卷一原卷版docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。
中考模拟卷（一）


一、单选题
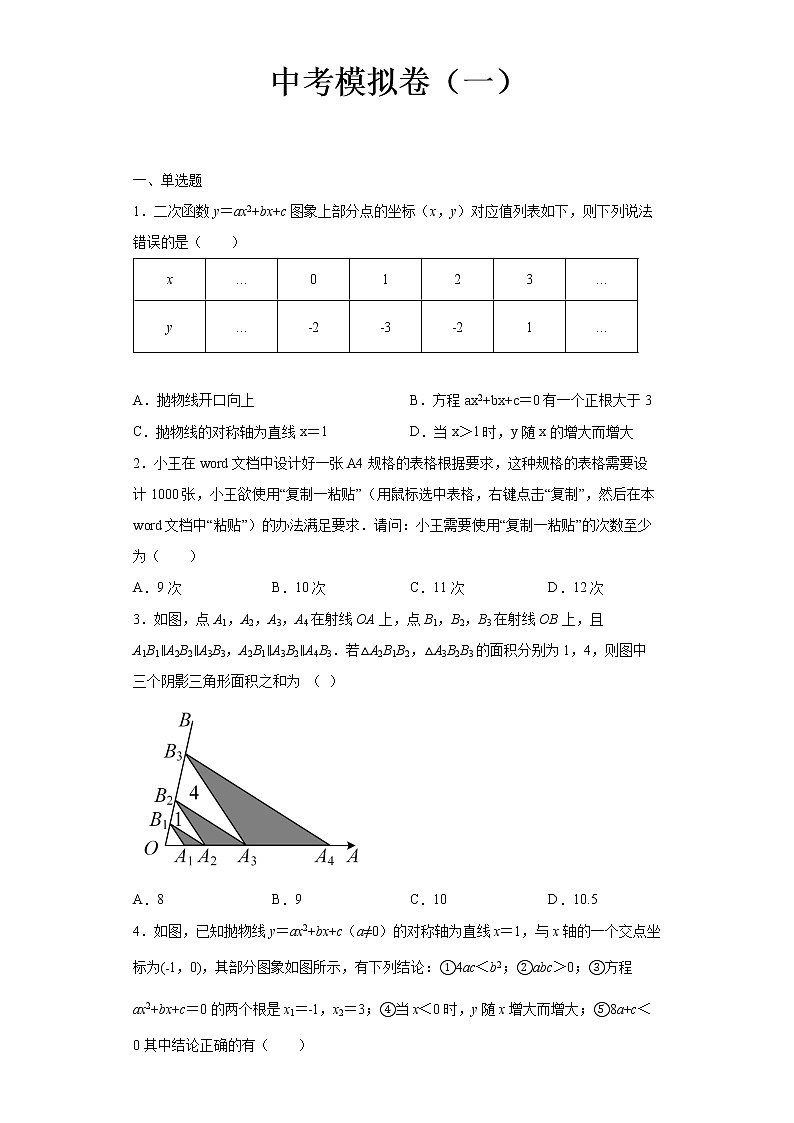
1．二次函数y＝ax2+bx+c图象上部分点的坐标（x，y）对应值列表如下，则下列说法错误的是（　　）
x
…
0
1
2
3
…
y
…
﹣2
﹣3
﹣2
1
…

A．抛物线开口向上 B．方程ax2+bx+c＝0有一个正根大于3
C．抛物线的对称轴为直线x＝1 D．当x＞1时，y随x的增大而增大
【答案】B
【分析】
首先根据表格中当和时，y都等于5，得出对称轴为，然后根据抛物线经过点（0，-2）得到抛物线开口向上，根据抛物线经过点（2，-2）和点（3，1）即可判断出方程ax2+bx+c＝0根的情况，根据抛物线的开口方向和对称轴即可判断抛物线的增减性．
【详解】
解：∵二次函数经过点（0，-2）和点（2，-2），
∴二次函数的对称轴为，顶点坐标为（1，-3），
∴C选项正确；
∵抛物线与y轴交于点（0，-2），
∴抛物线开口向上，
∴A选项正确；
∵二次函数的对称轴为，经过点（2，-2）和点（3，1），
∴抛物线与x轴的正半轴交点的横坐标小于3，
∴方程ax2+bx+c＝0有一个正根小于3，
∴B选项错误；
∵抛物线开口向上，对称轴为，
∴当x＞1时，y随x的增大而增大，
∴D选项正确．
故选：B．
2．小王在word文档中设计好一张A4规格的表格根据要求，这种规格的表格需要设计1000张，小王欲使用“复制一粘贴”（用鼠标选中表格，右键点击“复制”，然后在本word文档中“粘贴”）的办法满足要求．请问：小王需要使用“复制一粘贴”的次数至少为（　　）
A．9次 B．10次 C．11次 D．12次
【答案】B
【分析】
根据题意得出第一次复制得2张，第二次复制最多得2×2=22=4张，第三次复制最多得2×2×2=23=8张，即可得出规律，第九次复制最多得29=512张，第十次复制最多得210=1024张，问题得解．
【详解】
解：由题意得第一次复制得2张，
第二次复制最多得2×2=22=4张，
第三次复制最多得2×2×2=23=8张，
第四次复制最多得2×2×2×2=24=16张，
……，
第九次复制最多得29=512张，
第十次复制最多得210=1024张，
1024＞1000，
所以至少需要10次．
故选：B
3．如图，点A1，A2，A3，A4在射线OA上，点B1，B2，B3在射线OB上，且A1B1∥A2B2∥A3B3，A2B1∥A3B2∥A4B3．若△A2B1B2，△A3B2B3的面积分别为1，4，则图中三个阴影三角形面积之和为 （ ）

A．8 B．9 C．10 D．10.5
【答案】D
【分析】
由题意得，，设A1B1，A2B2之间的距离为h，则由题意可得，再由可得，，从而得到问题的解答．
【详解】
∵A1B1∥A2B2
∴∠A1A2B1=∠A2A3B2
∵A2B1∥A3B2
∴∠A1A2B1=∠A2A3B2
∴ △A1A2B1∽△A2A3B2（AA）
同理可证△A2A3B2∽△A3A4B3，△A2B1B2∽△A3B2B3
∵△A2B1B2∽△A3B2B3，，
∴，
又∵△A1A2B1∽△A2A3B2
∴
设之间的距离为h，则：，
∴
又∵
∴
∴，
∵，△A1A2B1∽△A2A3B2
∴
∴，
同理有，
∴图中三个阴影三角形面积之和为：
，
故选：D．
4．如图，已知抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与x轴的一个交点坐标为(﹣1，0)，其部分图象如图所示，有下列结论：①4ac＜b2；②abc＞0；③方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3；④当x＜0时，y随x增大而增大；⑤8a+c＜0其中结论正确的有（　　）

A．2个 B．3个 C．4个 D．5个
【答案】C
【分析】
由抛物线与x轴有2个交点即，可判断①；由抛物线开口向下，与y轴交于正半轴，而对称轴在y轴右侧，可判断a、b、c的正负即可判断②；由抛物线的对称轴为直线，点关于直线的对称点的坐标为即可判断③；由抛物线的对称轴为直线，可判断④；由对称轴，可得，图象可知，当时，，代入化简即可判断⑤．
【详解】
解：∵抛物线与x轴有2个交点，
∴，即，
∴①正确．
∵抛物线开口向下，与y轴交于正半轴，
∴，而对称轴在y轴右侧，
∴，而，
∴，因此，，
∴②错误．
∵抛物线的对称轴为直线，而点关于直线的对称点的坐标为，
∴方程的两个根是，
∴③正确．
∵抛物线的对称轴为直线，
∴当时，y随x增大而增大，
∴④正确．
∵，即，
观察图象可知，当时，，
∴，即，
∴⑤正确．
综上所述，①③④⑤正确，正确结论有4个，
故选C．
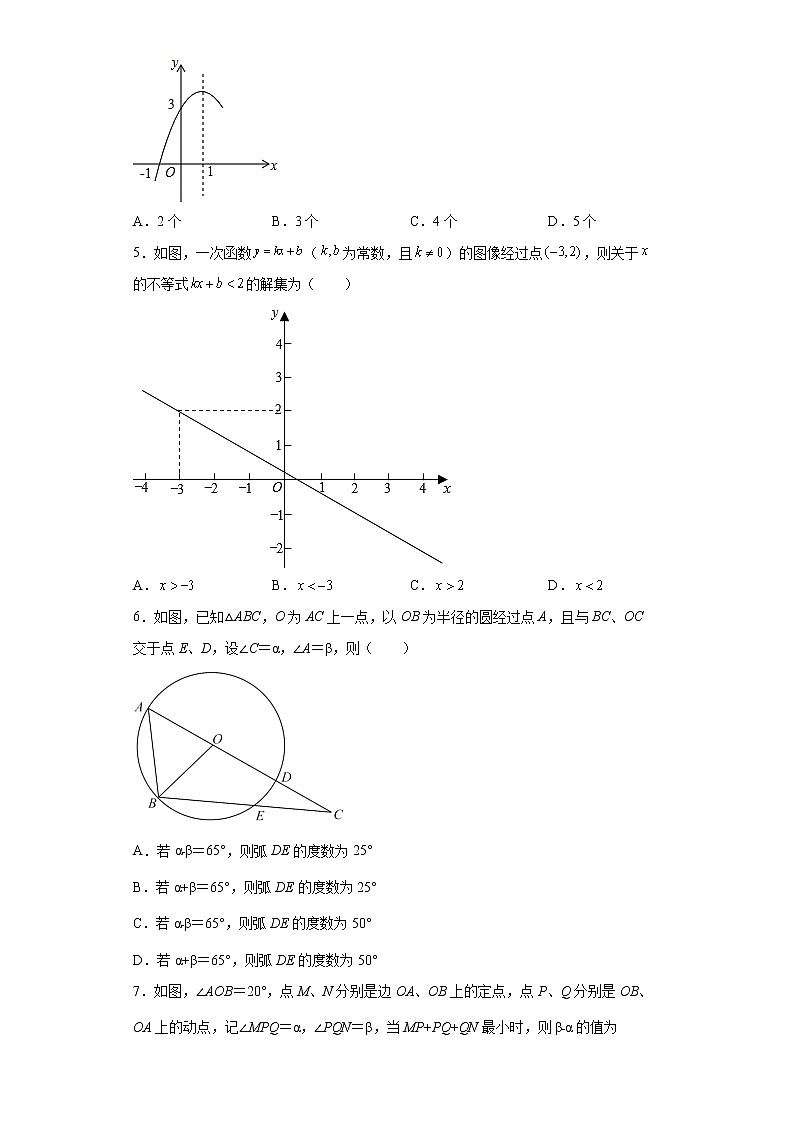
5．如图，一次函数（为常数，且）的图像经过点，则关于的不等式的解集为（ ）

A． B． C． D．
【答案】A
【分析】
根据图像的意义当x=-3时，kx+b=2，根据一次函数的性质求解即可．
【详解】
解：∵当x=-3时，kx+b=2，
且y随x的增大而减小，
∴不等式的解集，
故选A．
6．如图，已知△ABC，O为AC上一点，以OB为半径的圆经过点A，且与BC、OC交于点E、D，设∠C＝α，∠A＝β，则（　　）

A．若α﹣β＝65°，则弧DE的度数为25°
B．若α+β＝65°，则弧DE的度数为25°
C．若α﹣β＝65°，则弧DE的度数为50°
D．若α+β＝65°，则弧DE的度数为50°
【答案】D
【分析】
连接BD，根据圆周角定理求出∠ABD＝90°，求出∠ADB＝90°﹣β，再根据三角形外角性质得出90°﹣β＝α+x，求出的度数是180°﹣2（α+β），再逐个判断即可．
【详解】
解答：解：连接BD，

设的度数是x，
则∠DBC＝x，
∵AC过O，
∴∠ABD＝90°，
∵∠A＝β，
∴∠ADB＝90°﹣β，
∵∠C＝α，∠ADB＝∠C+∠DBC，
∴90°﹣β＝α+x，
解得：x＝180°﹣2（α+β），
即的度数是180°﹣2（α+β），
当α﹣β＝65°，即α＝65°+β时，的度数是180°﹣2（65°+β+β）＝50°﹣4β或180°﹣（α+α﹣65°）＝245°﹣2α，故选项A，C不符合题意；
当α+β＝65°时，的度数是180°﹣130°＝50°，故选项B错误，选项D正确；
故选：D．
7．如图，∠AOB＝20°，点M、N分别是边OA、OB上的定点，点P、Q分别是OB、OA上的动点，记∠MPQ＝α，∠PQN＝β，当MP+PQ+QN最小时，则β﹣α的值为（　　）


A．10° B．20° C．40° D．50°
【答案】C
【分析】
作M关于OB的对称点，N关于OA的对称点，连接交OA于Q，交OB于P，则MP＋PQ＋QN最小易知∠OPM＝∠OP＝∠NPQ，∠OQP＝∠AQ＝∠AQN，根据三角形的外角的性质和平角的定义即可得到结论．
【详解】
解：如图，作M关于OB的对称点，N关于OA的对称点，连接交OA于Q，交OB于P，则MP＋PQ＋QN最小，

∴∠OPM＝∠OP＝∠NPQ，∠OQP＝∠AQ＝∠AQN，
∴∠QPN＝（180°−α）＝∠AOB＋∠MQP＝20°＋（180°−β），
∴180°−α＝40°＋（180°−β），
∴β−α＝40°，
故选：C．
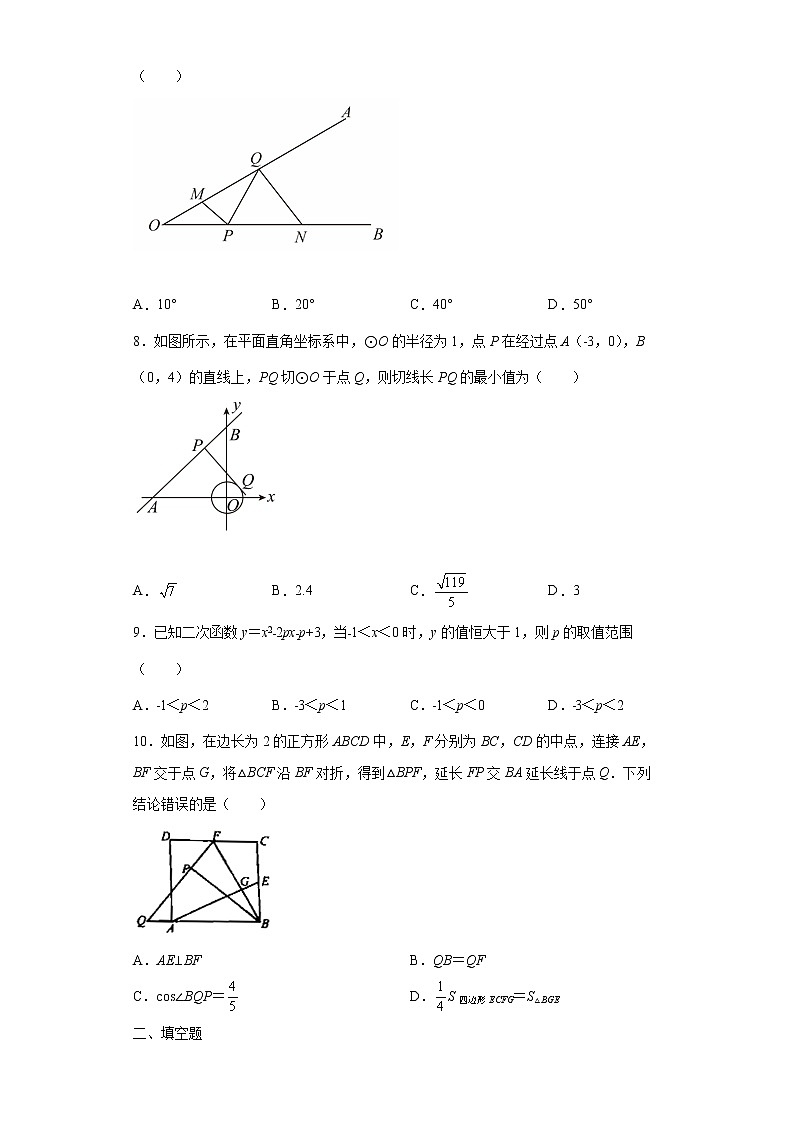
8．如图所示，在平面直角坐标系中，⊙O的半径为1，点P在经过点A（﹣3，0），B（0，4）的直线上，PQ切⊙O于点Q，则切线长PQ的最小值为（　　）


A． B．2.4 C． D．3
【答案】C
【分析】
由切线的性质可知，线段PQ、OP、OQ组成直角三角形，其中OQ为半径，是个定值，勾股定理可知，当切线PQ最短时，必有OP最短，由此当时，此时切线长PQ有最小值，通过三角形等面积法求出PQ，再利用勾股定理求出PQ．
【详解】
解：如图所示：连接OP、OQ，


PQ切⊙O于点Q，
，为直角三角形，
由勾股定理可知：，
故当OP有最小值时，PQ也有最小值,
根据点到直线距离，垂线段最短可知：当，OP有最小值，
如下图所示：过点O向AB作垂线，垂足为P，并在圆上找到对应切点Q，连接PQ与OQ．


点A（﹣3，0），B（0，4）,
，,
在中，由勾股定理可得：,
利用等面积法可得： 　解得：
故，
故选：C．
9．已知二次函数y＝x2﹣2px﹣p+3，当﹣1＜x＜0时，y的值恒大于1，则p的取值范围（　　）
A．﹣1＜p＜2 B．﹣3＜p＜1 C．﹣1＜p＜0 D．﹣3＜p＜2
【答案】D
【分析】
将x=-1代入函数的解析式，令y>1即可求得p的取值范围．
【详解】
解：二次函数 的图象是一条开口向上的抛物线，
(1)当抛物线的对称轴x= p≤-1时，只要使二次函数解析式的值-1  -3；
(2) 当抛物线的对称轴x= p≥0时，只要使二次函数解析式的值-1