2023 数学新中考二轮复习热点透析 核心考点10图形的变化

这是一份2023 数学新中考二轮复习热点透析 核心考点10图形的变化，文件包含2023数学新中考二轮复习热点透析核心考点10图形的变化解析版docx、2023数学新中考二轮复习热点透析核心考点10图形的变化原卷版docx等2份试卷配套教学资源，其中试卷共108页， 欢迎下载使用。
核心考点10 图形的变化
考向分析
1．从考查的题型来看，本知识点主要以填空题或选择题的形式考查，题目简单，属于低档题。
2．从考查内容来看,涉及本知识点的重点有平移的性质与旋转的性质；轴对称的性质；中心对称与中心对称图形的概念；轴对称与轴对称图形的概念。
3．从考查热点来看,涉及本知识点的主要有平移、旋转、轴对称的性质；轴对称与轴对称图形；中心对称与中心对称图形；用轴对称、平移、旋转的性质作图。
考点详解
1．判断图形的平移
（1）把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同，图形的这种移动叫做平移变换，简称平移．
方法归纳：平移前后，图形的形状、大小一样．
（2）作已知图形的平移图形
画平移图形，必须找出平移方向和距离，其依据是平移的性质．
2．识别中心对称图形
把一个图形绕着某一个点旋转180°，如果旋转后的图形能够和原来的图形互相重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．
方法归纳：解这类问题的关键是看图形旋转180°之后是否能完全重合．是旋转不是翻折．
3．旋转的性质
（1）图形中的每一点都绕着旋转中心旋转了同样大小的角度；
（2）对应点到旋转中心的距离相等；
（3）对应角、对应线段相等；
（4）图形的形状和大小都不变.
4．识别轴对称图形
（1）基础知识归纳：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴．
方法归纳：解这类问题的关键是看图形翻折180°之后是否能完全重合．对称轴是直线．
（2）作已知图形的轴对称图形
如果两个图形关于某条直线对称，那么对称轴是任意一对对应点所连线段的垂直平分线．
方法归纳：过点作对称轴的垂线并延长倍长找到对应点．是翻折不是旋转．
（3）轴对称性质的应用
轴对称图形的对称轴，是任意一对对应点所连线段的垂直平分线，对应线段、对应角相等．
真题再现
一、单选题
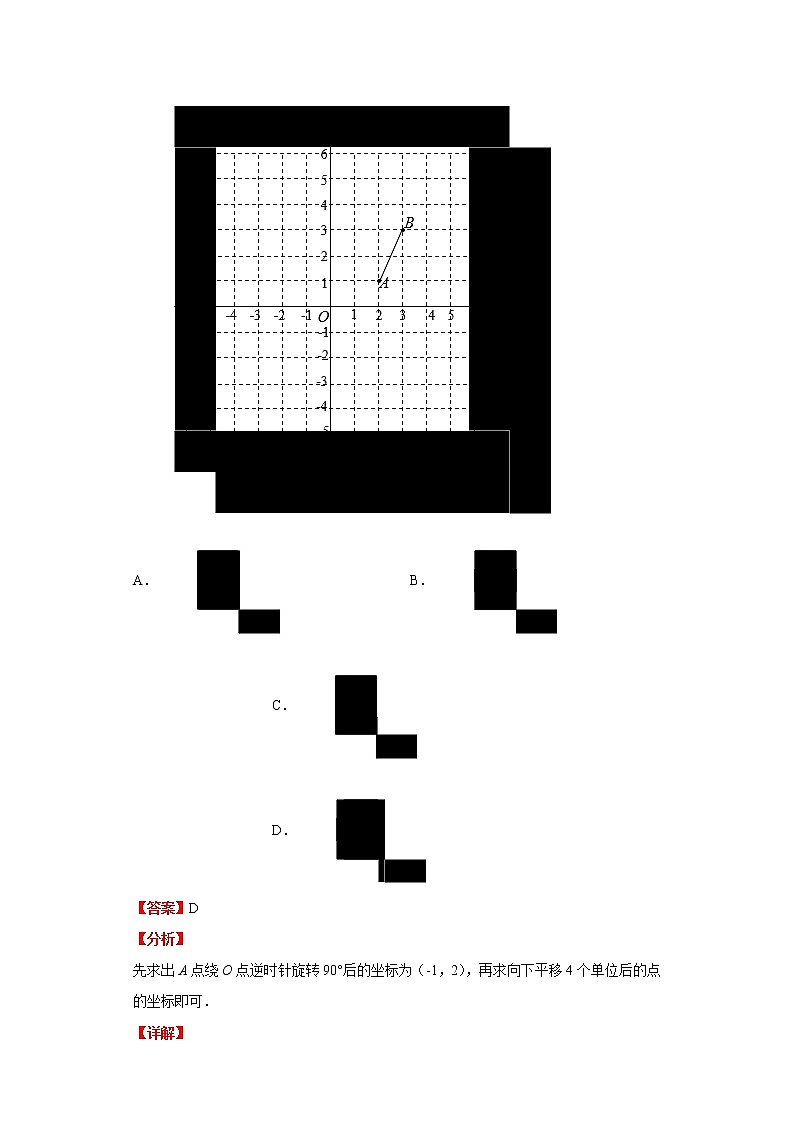
1．（2021·山东青岛·中考真题）如图，将线段先绕原点按逆时针方向旋转，再向下平移4个单位，得到线段，则点的对应点的坐标是（       ）

A． B． C． D．
【答案】D
【分析】
先求出A点绕O点逆时针旋转90°后的坐标为（-1，2），再求向下平移4个单位后的点的坐标即可．
【详解】
解：如图连接OA,将OA点绕O点逆时针旋转90°，得到点A''（-1，2），A''向下平移4个单位，得到A'（-1，-2）；

故选：D．
2．（2021·山东日照·中考真题）在平面直角坐标系中，把点向右平移两个单位后，得到对应点的坐标是（　　）
A． B． C． D．
【答案】D
【分析】
根据平移时，点的坐标变化规律“左减右加”进行计算即可．
【详解】
解：根据题意，从点到点，点的纵坐标不变，横坐标是，
故点的坐标是．
故选：D．
3．（2021·四川雅安·中考真题）如图，将沿边向右平移得到，交于点G．若．．则的值为（       ）

A．2 B．4 C．6 D．8
【答案】B
【分析】
根据平移的性质可得AD=BE，且AD∥BE，故可得△CEG∽△ADG，由相似三角形的性质及已知条件即可求得△CEG的面积．
【详解】
由平移的性质可得：AD=BE，且AD∥BE
∴△CEG∽△ADG
∴
即
∵
∴
∴
∵
∴
故选：B．
4．（2021·辽宁鞍山·中考真题）下列四幅图片上呈现的是垃圾类型及标识图案，其中标识图案不是轴对称图形的是（       ）
A． B．
C． D．
【答案】B
【分析】
根据轴对称的定义：图形两部分沿对称轴折叠后可重合，结合各选项图案的特点即可得出答案．
【详解】
A.是轴对称图形，不符合题意，
B.不是轴对称图形，符合题意，
C.是轴对称图形，不符合题意，
D.是轴对称图形，不符合题意，
故选：B．
5．（2021·西藏·中考真题）如图，在Rt△ABC中，∠A＝30°，∠C＝90°，AB＝6，点P是线段AC上一动点，点M在线段AB上，当AM＝AB时，PB＋PM的最小值为（       ）

A．3 B．2 C．2＋2 D．3＋3
【答案】B
【分析】
作B点关于AC的对称点B'，连接B'M交AC于点P，则PB＋PM的最小值为B'M的长，过点B'作B'H⊥AB交H点，在Rt△BB'H中，B'H＝3，HB＝3，可求MH＝1，在Rt△MHB'中，B'M＝2，所以PB＋PM的最小值为2．
【详解】
解：作B点关于AC的对称点B'，连接B'M交AC于点P，
∴BP＝B'P，BC＝B'C，
∴PB＋PM＝B'P＋PM≥B'M，
∴PB＋PM的最小值为B'M的长，
过点B'作B'H⊥AB交H点，

∵∠A＝30°，∠C＝90°，
∴∠CBA＝60°，
∵AB＝6，
∴BC＝3，
∴BB'＝BC＋B'C＝6，
在Rt△BB'H中，∠B'BH＝60°，
∴∠BB'H＝30°，
∴BH＝3，
由勾股定理可得：，
∴AH＝AB－BH＝3，
∵AM＝AB，
∴AM＝2，
∴MH＝AH－AM＝1，
在Rt△MHB'中，，
∴PB＋PM的最小值为2，
故选：B．
6．（2021·广西桂林·中考真题）下列图形中，是轴对称图形的是（　　）
A． B． C． D．
【答案】B
【分析】
直接利用轴对称图形的定义得出答案．如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴．
【详解】
解：A．不是轴对称图形，不符合题意；
B．是轴对称图形，符合题意；
C．不是轴对称图形，不符合题意；
D.不是轴对称图形，不符合题意．
故选：B．
7．（2021·内蒙古鄂尔多斯·中考真题）如图，在中，，将边沿折叠，使点B落在上的点处，再将边沿折叠，使点A落在的延长线上的点处，两条折痕与斜边分别交于点N、M，则线段的长为（       ）


A． B． C． D．
【答案】B
【分析】
利用勾股定理求出AB=10，利用等积法求出CN＝，从而得AN＝，再证明∠NMC＝∠NCM＝45°，进而即可得到答案．
【详解】
解：∵
∴AB=，
∵S△ABC＝×AB×CN＝×AC×BC
∴CN＝，
∵AN＝，
∵折叠
∴AM＝A'M，∠BCN＝∠B'CN，∠ACM＝∠A'CM，
∵∠BCN+∠B'CN+∠ACM+∠A'CM=90°，
∴∠B'CN +∠A'CM＝45°，
∴∠MCN＝45°，且CN⊥AB，
∴∠NMC＝∠NCM＝45°，
∴MN＝CN＝，
∴A'M＝AM＝AN−MN＝-=．
故选B．
8．（2021·四川德阳·中考真题）如图，边长为1的正六边形ABCDEF放置于平面直角坐标系中，边AB在x轴正半轴上，顶点F在y轴正半轴上，将正六边形ABCDEF绕坐标原点O顺时针旋转，每次旋转60°，那么经过第2025次旋转后，顶点D的坐标为（　　）

A．（，） B．（，） C．（，） D．（，）
【答案】A
【分析】
如图，连接，．首先确定点的坐标，再根据6次一个循环，由，推出经过第2025次旋转后，顶点的坐标与第三次旋转得到的的坐标相同，由此即可解决问题．
【详解】
解：如图，连接，．
在正六边形中，，，，
，
在中，，，
，
，
，
，，
将正六边形绕坐标原点顺时针旋转，每次旋转，
次一个循环，
，
经过第2025次旋转后，顶点的坐标与第三次旋转得到的的坐标相同，
与关于原点对称，
，，
经过第2025次旋转后，顶点的坐标，，
故选：A．

9．（2021·黑龙江牡丹江·中考真题）如图，△AOB中，OA＝4，OB＝6，AB＝2，将△AOB绕原点O旋转90°，则旋转后点A的对应点A′的坐标是（       ）

A．（4，2）或（﹣4，2） B．（2，﹣4）或（﹣2，4）
C．（﹣2，2）或（2，﹣2） D．（2，﹣2）或（﹣2，2）
【答案】C
【分析】
先求出点A的坐标，再根据旋转变换中，坐标的变换特征求解；或根据题意画出图形旋转后的位置，根据旋转的性质确定对应点A′的坐标．
【详解】
过点A作于点C．
在Rt△AOC中， ．
在Rt△ABC中， ．
∴　．
∵OA＝4，OB＝6，AB＝2，
∴．
∴．
∴点A的坐标是．
根据题意画出图形旋转后的位置，如图，
∴将△AOB绕原点O顺时针旋转90°时，点A的对应点A′的坐标为；
将△AOB绕原点O逆时针旋转90°时，点A的对应点A′′的坐标为．

故选：C．
10．（2021·广东广州·中考真题）如图，在中，，，，将绕点A逆时针旋转得到，使点落在AB边上，连结，则的值为（       ）

A． B． C． D．
【答案】C
【分析】
由勾股定理求出，并利用旋转性质得出，，，则可求得，再根据勾股定理求出，最后由三角形函数的定义即可求得结果．
【详解】
解：在中，，，，
由勾股定理得：．
∵绕点A逆时针旋转得到，
∴，，．
∴．
∴在中，由勾股定理得．
∴．
故选：C．
11．（2021·湖北黄石·中考真题）如图，的三个顶点都在方格纸的格点上，其中点的坐标是，现将绕点按逆时针方向旋转，则旋转后点的坐标是（       ）


A． B． C． D．
【答案】B
【分析】
在网格中绘制出CA旋转后的图形，得到点C旋转后对应点．
【详解】
如图，绘制出CA绕点A逆时针旋转90°的图形，

由图可得：点C对应点的坐标为(-2，3) ．
故选B．
12．（2021·内蒙古通辽·中考真题）定义：一次函数的特征数为，若一次函数的图象向上平移3个单位长度后与反比例函数的图象交于A，B两点，且点A，B关于原点对称，则一次函数的特征数是（       ）
A． B． C． D．
【答案】D
【分析】
先求出平移后的直线解析式为，根据与反比例函数的图象交于A，B两点，且点A，B关于原点对称，得到直线经过原点，从而求出m，根据特征数的定义即可求解．
【详解】
解：由题意得一次函数的图象向上平移3个单位长度后解析式为，
∵直线与反比例函数的图象交于A，B两点，且点A，B关于原点对称，
∴点A，B，O在同一直线上，
∴直线经过原点，
∴m+3=0，
∴m=-3，
∴一次函数的解析式为，
∴一次函数的特征数是．
故选：D
13．（2021·湖北荆门·中考真题）下列图形既是中心对称又是轴对称的是（     ）
A． B． C． D．
【答案】C
【分析】
根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．
【详解】
解：A、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项不符合题意．
B、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，不是轴对称图形，故此选项不符合题意；
C、此图形旋转180°后能与原图形重合，此图形是中心对称图形，是轴对称图形，故此选项符合题意；
D、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，也不是轴对称图形，故此选项不符合题意．
故选：C．
14．（2021·四川广元·中考真题）下列图形均表示医疗或救援的标识，其中既是轴对称图形又是中心对称图形的是（       ）
A． B．
C． D．
【答案】C
【分析】
根据轴对称及中心对称图形的定义逐一判断即可得答案．
【详解】
A.是轴对称图形，但不是中心对称图形，故该选项不符合题意，
B.是轴对称图形，但不是中心对称图形，故该选项不符合题意，
C.是轴对称图形，又是中心对称图形，故该选项符合题意，
D.既不是轴对称图形，又不是中心对称图形，故该选项不符合题意，
故选：C.
15．（2021·山东菏泽·中考真题）如图是一个几何体的三视图，根据图中所标数据计算这个几何体的体积为（       ）


A． B． C． D．
【答案】B
【分析】
根据三视图可以确定该几何体是空心圆柱体，再利用已知数据计算空心圆柱体的体积．
【详解】
解：先由三视图确定该几何体是空心圆柱体，底面外圆直径是4，内圆直径是2，高是6．
空心圆柱体的体积为π×2×6-π×2×6=18π．
故选：B．
二、填空题
16．（2021·江苏淮安·中考真题）如图（1），△ABC和△A′B′C′是两个边长不相等的等边三角形，点B′、C′、B、C都在直线l上，△ABC固定不动，将△A′B′C′在直线l上自左向右平移．开始时，点C′与点B重合，当点B′移动到与点C重合时停止．设△A′B′C′移动的距离为x，两个三角形重叠部分的面积为y，y与x之间的函数关系如图（2）所示，则△ABC的边长是___．

【答案】5
【分析】
在点B'到达B之前，重叠部分的面积在增大，当点B'到达B点以后，且点C'到达C以前，重叠部分的面积不变，之后在B'到达C之前，重叠部分的面积开始变小，由此可得出B'C'的长度为a，BC的长度为a＋3，再根据△ABC的面积即可列出关于a的方程，求出a即可．
【详解】
解：当点B'移动到点B时，重叠部分的面积不再变化，
根据图象可知B'C'＝a，，
过点A'作A'H⊥B'C'，
则A'H为△A'B'C'的高，

∵△A'B'C'是等边三角形，
∴∠A'B'H＝60°，
∴sin60°＝，
∴A'H＝，
∴，即，
解得a＝﹣2（舍）或a＝2，
当点C'移动到点C时，重叠部分的面积开始变小，
根据图像可知BC＝a＋3＝2＋3＝5，
∴△ABC的边长是5，
故答案为5．
17．（2021·江苏镇江·中考真题）如图，等腰三角形ABC中，AB＝AC，BC＝6，cos∠ABC＝，点P在边AC上运动（可与点A，C重合），将线段BP绕点P逆时针旋转120°，得到线段DP，连接BD，则BD长的最大值为__．

【答案】9
【分析】
由旋转知△BPD是顶角为120°的等腰三角形，可求得BD＝BP，当BP最大时，BD取最大值，即点P与点A重合时，BP＝BA最大，求出AB的长即可解决问题．
【详解】
解：∵将线段BP绕点P逆时针旋转120°，得到线段DP，
∴BP＝PD，
∴△BPD是等腰三角形，
∴∠PBD＝30°，
过点P作PH⊥BD于点H，

∴BH＝DH，
∵cos30°＝＝，
∴BH＝BP，
∴BD＝BP，
∴当BP最大时，BD取最大值，即点P与点A重合时，BP＝BA最大，
过点A作AG⊥BC于点G，
∵AB＝AC，AG⊥BC，
∴BG＝BC＝3，
∵cos∠ABC＝，
∴，
∴AB＝9，
∴BD最大值为：BP＝9．
故答案为：9．
18．（2021·浙江衢州·中考真题）将一副三角板如图放置在平面直角坐标系中，顶点A与原点O重合，AB在x轴正半轴上，且，点E在AD上，，将这副三角板整体向右平移_______个单位，C，E两点同时落在反比例函数的图象上．

【答案】
【分析】
分别求出，，假设向右平移了m个单位，将平移后的店代入中，列出方程进行求解即可．
【详解】
过E作EN⊥DB, 过C作CM⊥BD，
∴，

由三角板及 ，可知，BD=12，CM=BM=DB=6，
∴ ，
∵，，
∴EN//OB，
∵
∴，
∴．
设将这副三角板整体向右平移m个单位，C，E两点同时落在反比例函数的图象上．
∵，，
∴平移后，，
∴，
∴，
解得．
经检验：是原方程的根，且符合题意，
故答案为：．
19．（2021·青海西宁·中考真题）如图，是等边三角形，，N是的中点，是边上的中线，M是上的一个动点，连接，则的最小值是________．

【答案】
【分析】
根据题意可知要求BM+MN的最小值，需考虑通过作辅助线转化BM，MN的值，从而找出其最小值，进而根据勾股定理求出CN，即可求出答案．
【详解】
解：连接CN，与AD交于点M，连接BM．（根据两点之间线段最短；点到直线垂直距离最短），是边上的中线即C和B关于AD对称，则BM+MN=CN，则CN就是BM+MN的最小值．

∵是等边三角形，，N是的中点，
∴AC=AB=6,AN=AB=3, ,
∴.
即BM+MN的最小值为．
故答案为：.
20．（2021·四川巴中·中考真题）如图，把边长为3的正方形OABC绕点O逆时针旋转n°（0＜n＜90）得到正方形ODEF，DE与BC交于点P，ED的延长线交AB于点Q，交OA的延长线于点M．若BQ：AQ＝3：1，则AM＝__________．

【答案】
【分析】
连接OQ，OP，利用HL证明Rt△OAQ≌Rt△ODQ，得QA=DQ，同理可证：CP=DP，设CP=x，则BP=3-x，PQ=x+，在Rt△BPQ中，利用勾股定理列出方程求出x=，再利用△AQM∽△BQP可求解．
【详解】
解：连接OQ，OP，

∵将正方形OABC绕点O逆时针旋转n°（0＜n＜90）得到正方形ODEF，
∴OA=OD，∠OAQ=∠ODQ=90°，
在Rt△OAQ和Rt△ODQ中，
，
∴Rt△OAQ≌Rt△ODQ（HL），
∴QA=DQ，
同理可证：CP=DP，
∵BQ：AQ=3：1，AB=3，
∴BQ=，AQ=，
设CP=x，则BP=3-x，PQ=x+，
在Rt△BPQ中，由勾股定理得：
(3-x)2+()2=(x+)2，
解得x=，
∴BP=，
∵∠AQM=∠BQP，∠BAM=∠B，
∴△AQM∽△BQP，
∴，
∴，
∴AM=．
故答案为：．
21．（2021·山东聊城·中考真题）有四张大小和背面完全相同的不透明卡片，正面分别印有等边三角形、平行四边形、菱形和圆，将这四张卡片背面朝上洗匀，从中随机抽取两张卡片，所抽取的卡片正面上的图形都既是轴对称图形，又是中心对称图形的概率是__________．
【答案】
【分析】
由等边三角形、平行四边形、菱形、圆中，既是中心对称图形，又是轴对称图形的有菱形、圆，再画出树状图展示所有等可能的结果，进而即可求得答案．
【详解】
解：设等边三角形、平行四边形、菱形、圆分别为A，B，C，D，
根据题意画出树状图如下：

一共有12种情况，抽出的两张卡片的图形既是中心对称图形，又是轴对称图形为C、D共有2种情况，
∴P（既是中心对称图形，又是轴对称图形）＝2÷12＝．
故答案是：．
三、解答题
22．（2021·甘肃兰州·中考真题）如图1，二次函数的图象交坐标轴于点，，点为轴上一动点．

（1）求二次函数的表达式；
（2）过点作轴分别交线段，抛物线于点，，连接．当时，求的面积；
（3）如图2，将线段绕点逆时针旋转90得到线段．
①当点在抛物线上时，求点的坐标；
②点在抛物线上，连接，当平分时，直接写出点P的坐标．
【答案】（1）；（2）；（3）①或；②或．
【分析】
（1）根据点的坐标以及已知条件，将的坐标代入即可求得的值，进而求得抛物线的解析式；
（2）依题意根据（1）的解析式求得的坐标，进而求得，据此求得，根据进而求得的坐标，根据即可求得的面积；
（3）①过作轴，分点在轴上方和下方两种情况讨论，证明，设，将点的坐标代入（1）中抛物线解析式中即可求得点的坐标情形2，方法同情形1；
②分当不平行于轴和轴两种情况讨论，当当不平行于轴时，过点作交于点,过点作于点，证明进而可得的坐标，当轴时，结合已知条件即可求得的坐标．
【详解】
（1）二次函数的图象经过

解得


（2）由，令
解得


当时，

,则
；
（3）如图，当点在轴下方时，过点作于点，

由，令，
解得
，
，
将线段绕点逆时针旋转90得到线段，





，，
设，


点在抛物线上，

解得（舍）

当点在轴上方时，如图，

过点作于点，设
同理可得


点在抛物线上，

解得（舍去），

综上所述，或；
②当不平行于轴时，过点作交于点,过点作于点，如图，

平分，，
，
,
，








当不平行于轴时，重合，
，


当轴时，如图，

此时
则
综上所述，当平方时，点的坐标为或．
23．（2021·青海西宁·中考真题）如图，正比例函数与反比例函数的图象交于点A，轴于点B，延长AB至点C，连接．若，．

（1）求的长和反比例函数的解析式；
（2）将绕点旋转90°，请直接写出旋转后点A的对应点A'的坐标．
【答案】（1），；（2）或
【分析】
（1）由三角函数值，即可求出OB=2，然后求出点A的坐标，即可求出反比例函数的解析式；
（2）根据题意，可分为：顺时针旋转90度和逆时针旋转90度，两种情况进行分析，即可得到答案．
【详解】
解：（1） ∵轴于点B
∴
在中，，
∴，
∴点A的横坐标为2
又∵点A在正比例函数的图象上
∴，
∴
把代入，得
∴，
∴反比例函数的解析式是 ；
（2）根据题意，
∵点A为（2，1），
∵将绕点旋转90°，
则分为：顺时针旋转90度和逆时针旋转90度，如图：

∴或．
24．（2021·甘肃兰州·中考真题）在中，，，，将绕点顺时针旋转，角的两边分别交射线于，两点，为上一点，连接，且（当点，重合时，点，也重合）．设，两点间的距离为，，两点间的距离为．

小刚根据学习函数的经验，对因变量随音自变量的变化而变化的规律进行了探究．
下面是小刚的探究过程，请补充完整．
（1）列表：下表的已知数据是根据，两点间的距离进行取点，画图，测量分别得到了与的几组对应值；

0

1

2

3

4

5
6
7
8
















请你通过计算补全表格：______；
（2）描点、连线：在平面直角坐标系中，描出表中各组数值所对应的点，并画出函数关于的图像；

（3）探究性质：随着自变量的不断增大，函数的变化趋势；
（4）解决问题：当时，的长度大约是______．（结果保留两位小数）
【答案】（1）；（2）见解析；（3）随着自变量的不断增大，函数不断减小；（4）
【分析】
（1）根据题意画出图形，证明，根据相似三角形性质可得结果；
（2）描点连线画出图形即可；
（3）根据（2）画出图像判断增减性即可；
（4）根据，可得，画出与（2）中图像交点即为所求．
【详解】
解：（1）当时，即两点之间的距离为，
旋转至如图所示时：

∴此时点和点C重合，
∵，，
∴，
∴，
∵，，，
∴，
∴，
∴，
故答案为：；
（2）函数图像如下图：
；
（3）根据图像可知：随着自变量的不断增大，函数不断减小；
（4）∵，
∴，
如图：与（2）中函数图像交点即为所求

∴，
即的长度大约是：cm，
故答案为：．
25．（2021·四川绵阳·中考真题）如图，点是的边上的动点，，连接，并将线段绕点逆时针旋转得到线段．

（1）如图1，作，垂足在线段上，当时，判断点是否在直线上，并说明理由；
（2）如图2，若，，求以、为邻边的正方形的面积．
【答案】（1）点在直线上，见解析；（2）18
【分析】
（1）根据，，得到，可得线段逆时针旋转落在直线上，即可得解；
（2）作于，得出，再根据平行线的性质得到，再根据直角三角形的性质计算即可；
【详解】
解：（1）结论：点在直线上；
∵，，
∴，
∴，即．
∴线段逆时针旋转落在直线上，即点在直线上．

（2）作于，
∵，，
∴，
∵，
∴，
∵，，
∴，，
∴，即以、为邻边的正方形面积．

26．（2021·四川德阳·中考真题）如图，点E是矩形ABCD的边BC上一点，将△ABE绕点A逆时针旋转至△AB1E1的位置，此时E、B1、E1三点恰好共线．点M、N分别是AE和AE1的中点，连接MN、NB1．

（1）求证：四边形MEB1N是平行四边形；
（2）延长EE1交AD于点F，若EB1＝E1F，，判断△AE1F与△CB1E是否全等，并说明理由．
【答案】（1）见解析；（2）全等，理由见解析
【分析】
（1）可证B1是EE1的中点，则EB1=EE1，根据M、N分别是AE和AE1的中点，则MN∥EB1，MN=EE1，即可证明；
（2）由S△EAF=S△FEC，可得AF=EC．然后通过SAS可证明结论．
【详解】
解：（1）证明：∵四边形ABCD是矩形，
∴∠B=90°，
∵△AB1E1是△ABE旋转所得的，
∴AE=AE1，∠AB1E1=∠AB1E=∠B=90°，
∴B1是EE1的中点，
∴EB1=EE1，
∵M、N分别是AE和AE1的中点，
∴MN∥EB1，MN=EE1，
∴EB1=MN，
∴四边形MEB1N为平行四边形，
（2）△AE1F≌△CEB1，
证明：连接FC，

∵EB1=B1E1=E1F，
∴=S△EAF，
同理，=SFEC，
∵=S△EB1C，
∴S△EAF=S△FEC，
∵AF∥EC，
∴△AEF底边AF上的高和△FEC底边上的高相等．
∴AF=EC．
∵AF∥EC，
∴∠AFE=∠FEC，
在△AE1F和△CEB1中，
，
∴△AE1F≌△CEB1（SAS）．
27．（2021·辽宁阜新·中考真题）下面是小明关于“对称与旋转的关系”的探究过程，请你补充完整．

（1）三角形在平面直角坐标系中的位置如图1所示，简称G，G关于y轴的对称图形为，关于轴的对称图形为．则将图形绕____点顺时针旋转____度，可以得到图形．
（2）在图2中分别画出G关于 y轴和直线的对称图形，．将图形绕____点（用坐标表示）顺时针旋转______度，可以得到图形．
（3）综上，如图3，直线和所夹锐角为，如果图形G关于直线的对称图形为，关于直线的对称图形为，那么将图形绕____点（用坐标表示）顺时针旋转_____度（用表示），可以得到图形．
【答案】（1）O，180；（2）图见解析，，90；（3），
【分析】
（1）根据图形可以直接得到答案；
（2）根据题意画出图形，观察图形，利用图形旋转的性质得到结论；
（3）从（1）（2）问的结论中得到解题的规律，求出两个函数的交点坐标，即可得出答案．
【详解】
解：（1）由图象可得，图形与图形关于原点成中心对称，
则将图形绕O点顺时针旋转180度，可以得到图形；
故答案为：O，180；
（2），如图；

由图形可得，将图形绕点（用坐标表示）顺时针旋转90度，可以得到图形，
故答案为：，90；
（3）∵当G关于y轴的对称图形为，关于轴的对称图形为时，与关于原点（0,0）对称，即图形绕O点顺时针旋转180度，可以得到图形；
当G关于 y轴和直线的对称图形，时，图形绕点（用坐标表示）顺时针旋转90度，可以得到图形，点（0,1）为直线与 y轴的交点，90度角为直线与 y轴夹角的两倍；
又∵直线和的交点为，夹角为，
∴当直线和所夹锐角为，图形G关于直线的对称图形为，关于直线的对称图形为，那么将图形绕点（用坐标表示）顺时针旋转度（用表示），可以得到图形．
故答案为：，．
28．（2021·浙江温州·中考真题）如图与的方格都是由边长为1的小正方形组成．图1是绘成的七巧板图案，它由7个图形组成，请按以下要求选择其中一个并在图2、图3中画出相应的格点图形（顶点均在格点上）．

（1）选一个四边形画在图2中，使点为它的一个顶点，并画出将它向右平移3个单位后所得的图形．
（2）选一个合适的三角形，将它的各边长扩大到原来的倍，画在图3中．
【答案】（1）见解析；（2）见解析
【分析】
（1）七巧板中有两个四边形，分别是正方形和平行四边形，根据题意可画出4种图形任意选一种即可，
（2）七巧板中有五个等腰直角三角形，有直角边长 的两个，直角边长2 的两个，直角边长2 的一个，根据题意利用数形结合的思想解决问题即可．
【详解】
解：（1）画法不唯一，当选四边形为正方形时可以是如图1或图2；当四边形式平行四边形时可以是图3或图4．

（2）画法不唯一，
当直角边长为时，扩大即直角边长为利用勾股定理画出直角边长为直角三角形可以是如图5或图6
当直角边长为2时，扩大即直角边长为2利用勾股定理画出直角边长为2直角 三角形可以是如图7或图8等．