2022-2023学年安徽省皖北地区高一上学期期末联考数学试题（解析版）

2022-2023学年安徽省皖北地区高一上学期期末联考数学试题

一、单选题

1．已知集合，，，则（    ）

A． B． C． D．

【答案】D

【分析】列举法表示集合后，根据补集和并集定义直接求解即可.

【详解】，，.

故选：D.

2．命题“"的否定是（    ）

A．

B．

C．

D．

【答案】D

【分析】根据全称命题的否定是特称命题即可求得结果．

【详解】命题“”的否定是“”.

故选：D．

3．若幂函数在区间上单调递减，则（    ）

A．3 B．1 C．或3 D．1或

【答案】A

【分析】由题目条件可得且.

【详解】因为函数为幂函数，且在区间上单调递减，所以且，又，可得或.

当时，满足，舍去；

当时，满足.

综上.

故选：A.

4．已知，则的值为（    ）

A． B． C． D．

【答案】A

【分析】利用诱导公式、三角函数的平方关系和商数关系求解即可.

【详解】由已知得，两边平方得，解得，

则原式.

故选：A

5．神舟十五号载人飞船搭载宇航员费俊龙､邓清明和张陆进入太空，在中国空间站将完成为期6个月的太空驻留任务，期间会进行很多空间科学实验.太空中的水资源极其有限，要通过回收水的方法制造可用水.回收水是将宇航员的尿液､汗液和太空中的水收集起来经过特殊的净水器处理成饮用水，循环使用.净化水的过程中，每增加一次过滤可减少水中杂质，要使水中杂质减少到原来的以下，则至少需要过滤的次数为（    ）（参考数据）

A．17 B．19 C．21 D．23

【答案】C

【分析】由指数、对数的运算性质求解即可

【详解】设过滤的次数为，原来水中杂质为1，

则由题意得，

即，

所以，

所以，

因为，

所以的最小值为21，

则至少要过滤21次.

故选：C.

6．若，则（    ）

A． B．

C． D．

【答案】B

【分析】化简得取中间值比较大小可得，即可比较大小.

【详解】

故

，

.

故选：B.

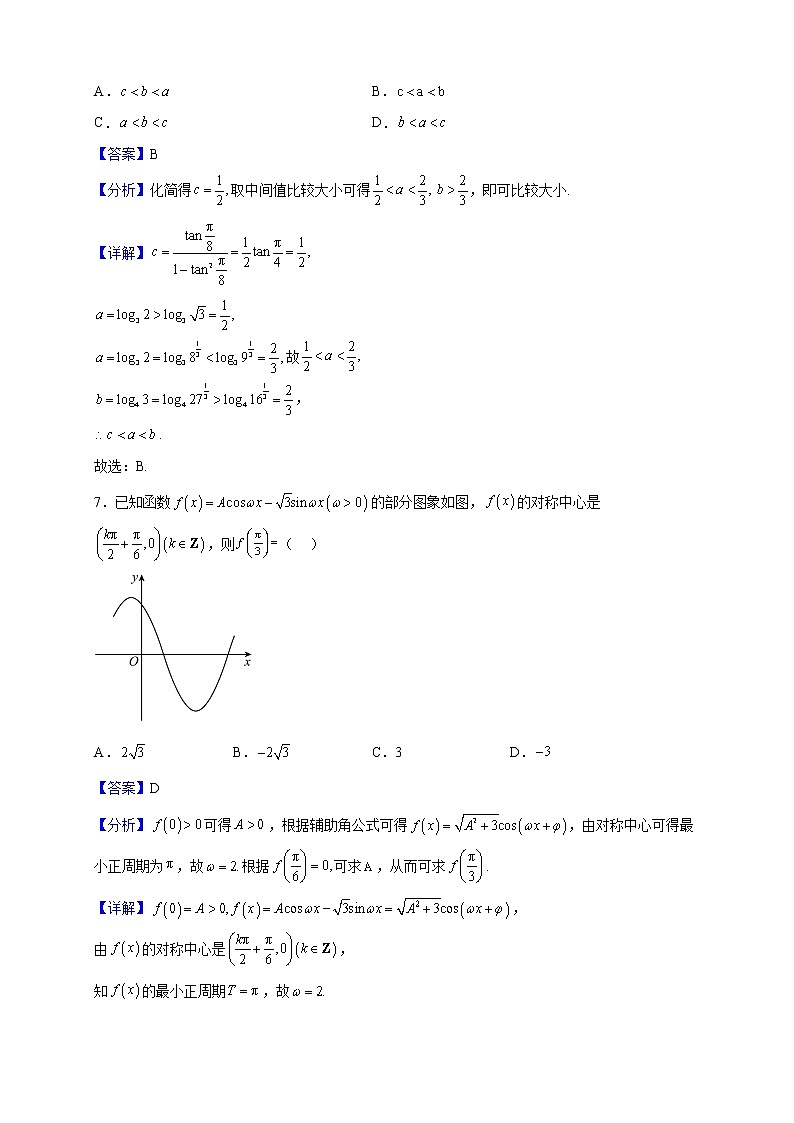
7．已知函数的部分图象如图，的对称中心是，则（    ）

A． B． C．3 D．

【答案】D

【分析】可得，根据辅助角公式可得，由对称中心可得最小正周期为，故根据可求，从而可求.

【详解】，

由的对称中心是，

知的最小正周期，故

故解得.

故.

故选:D.

8．函数在内的零点之和为（    ）

A． B． C． D．

【答案】C

【分析】根据反比例函数和正弦型函数的对称性可知与均关于对称，作出两函数图象，采用数形结合的方式可确定交点个数，结合对称性可得结果.

【详解】令，

关于点对称，关于点对称；

令，

关于点对称；

在内的零点即为与的图象在内的交点的横坐标，

作出与图象如下图所示，

由图象可知：与在内共有个交点，

由对称性可知：交点横坐标之和为，即在内的零点之和为.

故选：C.

【点睛】思路点睛：本题考查函数零点个数之和的问题，解决此类问题的基本思路是将问题转化为两个函数的交点横坐标之和，通过确定两个函数的对称性和交点个数来进行求解.

二、多选题

9．下列命题为真命题的是（    ）

A．是的必要条件

B．是的充分不必要条件

C．是的充分条件

D．的充要条件是

【答案】BD

【分析】根据充分条件、必要条件与充要条件的定义逐项判断即可.

【详解】必要性：，当时，此时错误；

由可推出但反之不行，所以是的充分不必要条件，B正确；

错误；

必要性：，

所以，

即，所以；

充分性：，则，D正确.

故选:BD.

10．设，用表示不超过的最大整数，则 称为高斯函数，也叫取整函数，例如.令函数，以下结论正确的有（    ）

A． B．

C．的值域为 D．的零点有2个

【答案】ABD

【分析】根据取整函数的定义，依次讨论各选项即可得答案；

【详解】解：，故A正确；

，故B正确；

由可知，为周期函数，且周期为1，

当时，，当时，，

当时，，当时，，

所以，的值域为，故C错误；

由为周期函数，且周期为1，所以，作出函数和的图像

由图可知，和的图像有2个交点，故有2个零点，故D正确.

故选：ABD.

11．若，且，则（    ）

A． B．

C． D．

【答案】ABD

【分析】由题意可得，根据可判断A；，利用“乘1法”可判断B；根据可判断C；可化为，利用基本不等式可判断D.

【详解】

∴，A正确；

，当且仅当时等号成立，B正确；

，解得错误；

，由题意知，，则，当且仅当时等号成立，D正确.

故选:ABD.

12．已知函数，下列说法正确的有（    ）

A．函数是最小正周期为的周期函数

B．函数在上单调递增

C．若方程在区间内有4个不同的根，则

D．函数在区间内，共有6个零点

【答案】BCD

【分析】求出与可判断A；可判断函数为偶函数，故求函数在上的单调性即可判断B；求出在时的单调性，画出图象，可判断CD.

【详解】因为，故函数不是以为周期的周期函数，故错误；

因为，

所以函数为偶函数.

当时，所以，

又，由在上为减函数，

所以函数在上单调递减，

则在上单调递增，故B正确；

当时，由得函数，

所以函数在且上为增函数，

在且上为减函数，

当时，由得函数，

所以函数在且上为增函数，

在且上为减函数，

作出图象如图所示，

则方程在区间内有4个不同的根，则，故正确；

因为函数为偶函数，函数在区间内的零点个数，只需确定在区间内的个数，由图象可知共有3个，所以在内共有6个零点，故D正确.

故选:.

三、填空题

13．杭州2022年第19届亚运会会徽（图1）象征着新时代中国特色社会主义大潮的涌动和发展，也象征亚奥理事会大家庭团结携手､紧密相拥､永远向前.图2是会徽抽象出的几何图形.设的长度是的长度是，几何图形的面积为，扇形的面积为，若，则__________.

【答案】8

【分析】由弧长比可得 ，再结合扇形面积公式求解.

【详解】因为，所以，

设扇形的面积为，则

则，所以，

所以，

故答案为：8.

14．已知函数，若不等式的解集非空，则的取值范围是__________.

【答案】

【分析】对进行分类讨论即可解决问题.

【详解】①当时，即时，

解集不是空集；

②当时，即时，

此时函数为开口向下的二次函数，

故不等式的解集非空；

③当0时，若不等式的解集非空，则

，

即，

综上，的取值范围是.

故答案为：.

15．计算：__________.

【答案】##

【分析】先切化弦，再根据二倍角的正弦公式、诱导公式、两角差的正弦公式化简即可得解.

【详解】

.

故答案为：

16．已知是定义在上的单调函数，且对任意都满足：

，则满足不等式的的范围是__________.

【答案】

【分析】由题可得为正常数，利用待定系数法可求得解析式，后利用对数函数的单调性解不等式即可得答案.

【详解】由题意得为正常数，令，则，且.

注意到函数，函数均在上单调递增，

则方程有唯一解.

原不等式等价于，

可得.

故答案为：.

四、解答题

17．计算下列各式的值.

(1)；

(2)设，求.

【答案】(1)

(2)

【分析】（1）根据指数和对数运算法则直接化简求解即可；

（2）根据指数和对数互化可表示出，根据可化简整理得到结果.

【详解】（1）原式.

（2）由得：，，

.

18．已知函数是定义在上的奇函数，当时，．

（1）求函数的解析式；

（2）①证明函数在上是单调递减函数；

②判断函数在上的单调性（不要证明）；

（3）根据你对该函数的理解，作出函数的图像．（不需要说明理由，但要有关键特征，标出关键点）

（本题可能使用到的公式：）

【答案】（1） （2）①详见解析②单调递增 （3）详见解析

【详解】试题分析：（1）可设x＜0，从而-x＞0，从而可求出，再根据f（0）=0便可用分段函数写出f（x）的解析式；（2）①x∈（0，1）时，，求导数，从而根据导数符号便可得出f（x）在（0，1）上为单调递减函数；②根据导数符号判断f（x）在[1，+∞）上的符号，从而得出其在[1，+∞）上的单调性；（3）f（x）为奇函数，从而图象关于原点对称，并且图象过原点，根据f（x）在（0，+∞）上的单调性画出其在（0，+∞）上的图象，再画出关于原点的对称图象即可

试题解析：（1）；

（2）①证明：设，，

则，

因为，所以，

，则，

所以，即函数在上是单调递减函数．

②单调递增．

（3）如图  

19．已知.

(1)求的值；

(2)求的值.

【答案】(1)

(2)

【分析】（1）首先根据两角和正切公式得到，再利用同角三角函数关系求解即可.

（2）首先根据两角和正切公式得到，即可得到.

【详解】（1），得；

.

（2）且得.

则，

因为，

又，得，

所以.

20．在①不等式的解集为，②当时，取得最大值4，③这三个条件中任选一个，补充在下面的问题中，并作答.

问题：已知函数，且__________.

(1)求的解析式；

(2)若在上的值域为，求的值.

【答案】(1)

(2)5

【分析】（1）对①：根据三个二次之间的关系运算求解；对②：根据二次函数的最值运算求解；对③：根据二次函数的对称性运算求解；（2）根据题意结合二次函数的单调性和最值分析运算.

【详解】（1）若选①：由函数，且不等式的解集为，

即是方程两个实数根，且，

可得，解得，

所以；

若选②：由题意可得，解得，

故；

若选③：因为，所以图象的对称轴方程为，

则，即，

因为，所以，

故.

（2）因为在上的值域为，所以，即，

因为图象的对称轴方程为，所以在上单调递减，

则，

解得，即.

21．已知函数为奇函数，且图象的相邻两对称轴间的距离为.

(1)当时，求的单调递减区间；

(2)将函数的图象向右平移个单位长度，再把横坐标缩小为原来的（纵坐标不变），得到函数的图象，记方程在上的根从小到大依次为，试确定的值，并求的值.

【答案】(1)

(2)，

【分析】(1)根据题意求出函数的解析式，并求出函数的完整减区间，结合给定区间即可求解；

(2)根据题意确定的解析式，从而得到解的个数，结合函数图象求解根的对称关系，可求解.

【详解】（1）由题意，函数，

因为函数图象的相邻两对称轴间的距离为，所以，可得，

又由函数为奇函数，可得，

所以，因为，所以，

所以函数，

令，解得，

函数的递减区间为，

再结合，可得函数的递减区间为.

（2）将函数的图象向右平移个单位长度，可得的图象，

再把横坐标缩小为原来的，得到函数的图象，

由方程，即，

即，

因为，可得，

设，其中，即，

结合正弦函数的图象，

可得方程在区间有5个解，即，

其中，

即

，

解得，

所以

22．已知函数为偶函数.

(1)求实数的值;

(2)解关于的不等式;

(3)设，若函数与图象有个公共点，求实数的取值范围.

【答案】(1)

(2)

(3)

【分析】（1）根据偶函数的定义及性质直接化简求值；

（2）判断时函数的单调性，根据奇偶性可得函数在各区间内的单调性，解不等式即可；

（3）由函数与图象有个公共点，可得有两个实数根，再利用换元法转化为二次方程有两个根，利用判别式求参数范围.

【详解】（1）函数的定义或为，

函数为偶函数.

，即 ，

，

；

（2），

当时，，单调递增，

在上单调递增，

又函数为偶函数，所以函数在上单调递增，在上单调递减；

，

，

解得或，

所以所求不等式的解集为 ；

（3）函数与图象有个公共点，

，

即，，

设，则，即，

又在上单调递增，

所以方程有两个不等的正根；

，

解得，即的取值范围为.