高考物理二轮复习专项分层特训专项4含答案

这是一份高考物理二轮复习专项分层特训专项4含答案，共9页。试卷主要包含了单项选择题，多项选择题，非选择题等内容，欢迎下载使用。

1.[2022·辽宁模拟卷]某小组的同学到劳动实践基地进行劳动锻炼，任务之一是利用石碾将作物碾碎，如图所示．两位男同学通过推动碾杆，可使碾杆和碾轮绕碾盘中心的固定竖直轴O转动，同时碾轮在碾盘上滚动，将作物碾碎．已知在推动碾轮转动的过程中，两位男同学的位置始终关于竖直轴对称，则下列选项中两男同学一定相同的是( )
A．线速度 B．角速度
C．向心加速度 D．向心力的大小
2.
[2022·全国甲卷]北京2022年冬奥会首钢滑雪大跳台局部示意图如图所示．运动员从a处由静止自由滑下，到b处起跳，c点为a、b之间的最低点，a、c两处的高度差为h.要求运动员经过c点时对滑雪板的压力不大于自身所受重力的k倍，运动过程中将运动员视为质点并忽略所有阻力，则c点处这一段圆弧雪道的半径不应小于( )
A． eq \f(h,k＋1) B． eq \f(h,k)
C． eq \f(2h,k) D． eq \f(2h,k－1)
3.[2022·广东卷]
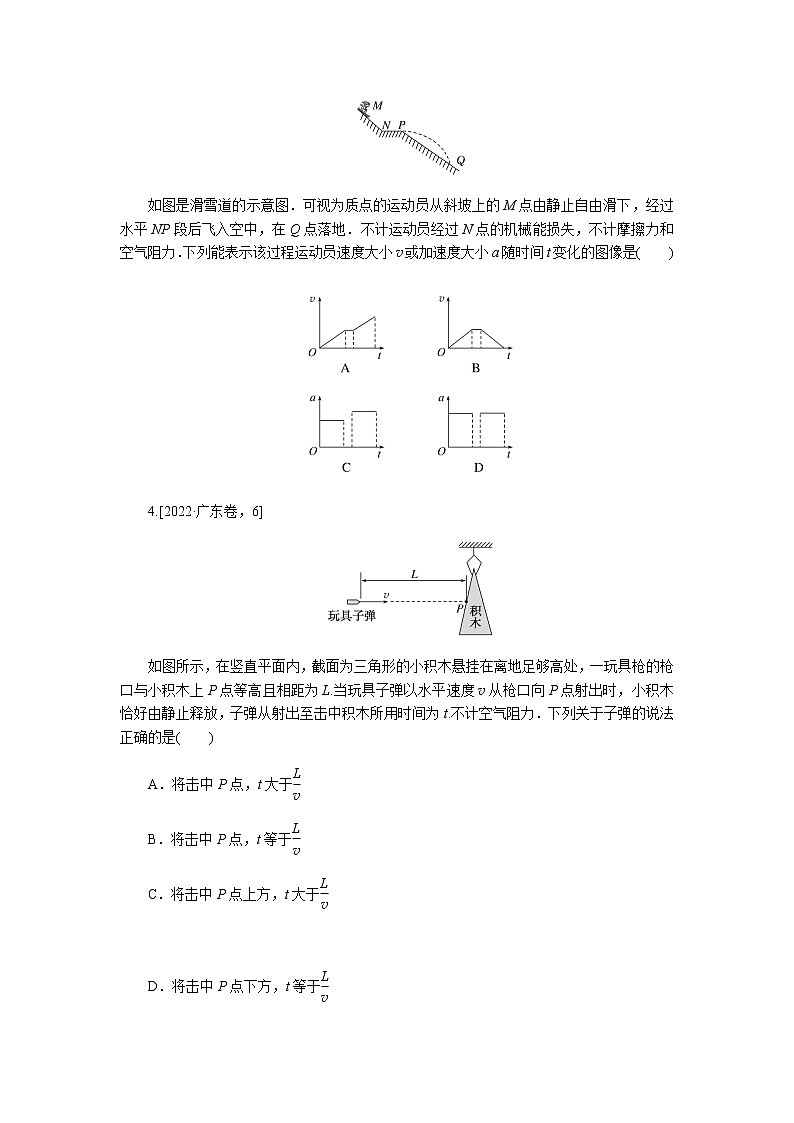
如图是滑雪道的示意图．可视为质点的运动员从斜坡上的M点由静止自由滑下，经过水平NP段后飞入空中，在Q点落地．不计运动员经过N点的机械能损失，不计摩擦力和空气阻力．下列能表示该过程运动员速度大小v或加速度大小a随时间t变化的图像是( )
4.[2022·广东卷，6]
如图所示，在竖直平面内，截面为三角形的小积木悬挂在离地足够高处，一玩具枪的枪口与小积木上P点等高且相距为L.当玩具子弹以水平速度v从枪口向P点射出时，小积木恰好由静止释放，子弹从射出至击中积木所用时间为t.不计空气阻力．下列关于子弹的说法正确的是( )
A．将击中P点，t大于 eq \f(L,v)
B．将击中P点，t等于 eq \f(L,v)
C．将击中P点上方，t大于 eq \f(L,v)
D．将击中P点下方，t等于 eq \f(L,v)
5.
[2022·广东茂名一模]大雾天气，司机以10 m/s的速度在水平路面上向前行驶，突然发现汽车已开到一个丁字路口(如图所示)，前方15 m处是一条小河，司机可采用紧急刹车或紧急转弯两种方法避险．已知汽车与地面之间的动摩擦因数为0.6，g＝10 m/s2，最大静摩擦力等于滑动摩擦力，下列措施中正确的是( )
A．紧急刹车 B．紧急转弯
C．两种都可以 D．两种都不可以
二、多项选择题
6.[2022·河北省模拟题]智能呼啦圈轻便美观，深受大众喜爱．如图甲，腰带外侧带有轨道，将带有滑轮的短杆穿入轨道，短杆的另一端悬挂一根带有配重的轻绳，其简化模型如图乙所示．可视为质点的配重质量为0.5 kg，绳长为0.5 m，悬挂点P到腰带中心点O的距离为0.2 m．水平固定好腰带，通过人体微小扭动，使配重随短杆做水平匀速圆周运动，绳子与竖直方向夹角为θ，运动过程中腰带可看作不动，重力加速度g取10 m/s2，sin 37°＝0.6，下列说法正确的是( )
A．匀速转动时，配重受到的合力恒定不变
B．若增大转速，腰带受到的合力变大
C．当θ稳定在37°时，配重的角速度为 eq \r(15) rad/s
D．当θ由37°缓慢增加到53°的过程中，绳子对配重做正功
7.
[2022·重庆二诊]如图所示，空间中匀强磁场的方向为竖直方向(图中未画出)，质量为m，电荷量为＋q的小球在光滑圆锥上以速度大小v做匀速圆周运动(从上往下看是逆时针)，其运动平面与圆锥轴线垂直且到圆锥顶点的距离为h，已知重力加速度为g，圆锥半顶角为θ，下列说法正确的是( )
A．磁场方向竖直向下
B．小球转一圈的过程中，重力的冲量为0
C．圆锥对小球的支持力大小为mg sin θ
D．磁感应强度大小为 eq \f(mg,qv tan θ) ＋ eq \f(mv,qh tan θ)
三、非选择题
8.[2022·全国甲卷]将一小球水平抛出，使用频闪仪和照相机对运动的小球进行拍摄，频闪仪每隔0.05 s发出一次闪光．某次拍摄时，小球在抛出瞬间频闪仪恰好闪光，拍摄的照片编辑后如图所示．图中的第一个小球为抛出瞬间的影像，每相邻两个球之间被删去了3个影像，所标出的两个线段的长度s1和s2之比为3∶7.重力加速度大小取g＝10 m/s2，忽略空气阻力．求在抛出瞬间小球速度的大小．
9.[2022·湖北省模拟题]2022年2月8日，18岁的中国选手谷爱凌在北京冬奥会自由式滑雪女子大跳台比赛中以绝对优势夺得金牌，这是中国代表团在北京冬奥会上的第三枚金牌，被誉为“雪上公主”的她赛后喜极而泣．现将比赛某段过程简化成如图可视为质点小球的运动，小球从倾角为α＝30°的斜面顶端O点以v0飞出，已知v0＝20 m/s，且与斜面夹角为θ＝60°.图中虚线为小球在空中的运动轨迹，且A为轨迹上离斜面最远的点，B为小球在斜面上的落点，C是过A作竖直线与斜面的交点，不计空气阻力，重力加速度取g＝10 m/s2.求：
(1)小球从O运动到A点所用时间t；
(2)小球离斜面最远的距离L；
(3)O、C两点间距离x.
10.动画片《熊出没》中有这样一个情节：某天熊大和熊二中了光头强设计的陷阱，被挂在了树上(如图甲)，聪明的熊大想出了一个办法，让自己和熊二荡起来使绳断裂从而得救，其过程可简化如图乙所示，设悬点为O，离地高度为2L，两熊可视为质点且总质量为m，绳长为 eq \f(L,2) 且保持不变，绳子能承受的最大张力为3mg，不计一切阻力，重力加速度为g，求：
(1)设熊大和熊二刚好在向右摆到最低点时绳子刚好断裂，则他们的落地点离O点的水平距离为多少；
(2)改变绳长，且两熊仍然在向右到最低点绳子刚好断裂，则绳长为多长时，他们的落地点离O点的水平距离最大，最大为多少；
(3)若绳长改为L，两熊在水平面内做圆锥摆运动，如图丙，且两熊做圆锥摆运动时绳子刚好断裂，则他们落地点离O点的水平距离为多少．
专项4 抛体运动和圆周运动
1．解析：线速度、向心加速度都是矢量，两同学的线速度和向心加速度的大小相等，但方向相反，所以不相同，故A、C错误；两同学的运动为同轴传动，故两者的角速度一定相同，故B正确；两同学的质量大小未知，所以无法判断两者所受向心力的大小关系，故D错误．
答案：B
2．解析：运动员从a处滑至c处，mgh＝ eq \f(1,2) mv eq \\al(\s\up1(2),\s\d1(c)) －0，在c点，N－mg＝m eq \f(v eq \\al(\s\up1(2),\s\d1(c)) ,R) ，联立得N＝mg eq \b\lc\(\rc\)(\a\vs4\al\c1(1＋\f(2h,R))) ，由题意，结合牛顿第三定律可知，N＝F压≤kmg，得R≥ eq \f(2h,k－1) ，故D项正确．
答案：D
3．解析：根据题述可知，运动员在斜坡上由静止滑下做加速度小于g的匀加速运动，在NP段做匀速直线运动，从P飞出后做平抛运动，加速度大小为g，速度方向时刻改变、大小不均匀增大，所以只有图像C正确．
答案：C
4．解析：由于子弹水平射出后做平抛运动，小积木做自由落体运动，二者竖直方向运动状态相同，所以将击中P点．子弹水平方向做匀速直线运动，由L＝vt可得t＝ eq \f(L,v) ，B项正确．
答案：B
5．解析：由题意知紧急刹车的位移为x＝ eq \f(v2,2a) ，又由牛顿第二定律得μmg＝ma，解得x≈8.3 m<15 m，故紧急刹车是安全的，转弯时静摩擦力提供向心力，最大静摩擦力为μmg，根据向心力公式有μmg＝ eq \f(mv2,rm) ，解得rm＝16.7 m>15 m，如果转弯半径小于rm＝16.7 m时需要更大的向心力，汽车容易发生侧翻是不安全的，选项A正确．
答案：A
6.
解析：匀速转动时，配重受到的合力提供向心力，大小恒定不变，方向指向圆心，时刻改变，故A错误；腰带受力平衡，受到的合力为0，故B错误；对配重受力分析如图所示：
根据向心力公式有：mg tan θ＝m（d＋l sin θ）ω2, d＝0.2, l＝0.5, θ＝37°，解得：ω＝ eq \r(15) rad/s，故C正确；当θ由37°缓慢增加到53°的过程中，需要加速，动能增加，同时配重高度上升，重力对配重做负功，故绳子对配重做正功，故D正确．
答案：CD
7．解析：由左手定则可知，磁场方向竖直向下，故A正确；小球转一圈的过程中，重力的冲量等于重力与时间的乘积，所以重力的冲量不等于零，故B错误；对小球进行受力分析可知，小球受到重力mg，垂直圆锥母线的支持力FN，水平方向的洛伦兹力qvB，沿水平和竖直方向正交分解，有FNsin θ＝mg, qvB－FNcs θ＝m eq \f(v2,h tan θ) ，解得FN＝ eq \f(mg,sin θ) ，磁感应强度大小为B＝ eq \f(mg,qv tan θ) ＋ eq \f(mv,qh tan θ) ，故C错误，D正确．
答案：AD
8.
解析：依题意，相邻两球影像间隔的时间t＝4t0＝0.2 s
设初速度大小为v0，如图所示：
由O到A，水平方向：x1＝v0t
竖直方向：y1＝ eq \f(1,2) gt2
又s1＝ eq \r(x eq \\al(\s\up1(2),\s\d1(1)) ＋y eq \\al(\s\up1(2),\s\d1(1)) )
由A到B，水平方向：x2＝v0t
竖直方向：y2＝ eq \f(1,2) g（2t）2－ eq \f(1,2) gt2
又s2＝ eq \r(x eq \\al(\s\up1(2),\s\d1(2)) ＋y eq \\al(\s\up1(2),\s\d1(2)) )
eq \f(s1,s2) ＝ eq \f(3,7)
联立解得v0＝ eq \f(2\r(5),5) m/s
答案： eq \f(2\r(5),5) m/s
9.
解析：（1）将速度分解，如图，当小球速度与斜面平行时到达A点
垂直斜面方向：v1＝v0sin θ，a1＝g cs α，t＝ eq \f(v1,α1) ，得：t＝2 s
（2）垂直斜面方向v1匀减速至0时有：L＝ eq \f(v eq \\al(\s\up1(2),\s\d1(1)) ,2a1) ，
代入数据得：L＝10 eq \r(3) m
（3）由垂直斜面方向运动对称性可得小球从O到A与A到B所用时间相等
平行斜面方向：a2＝g sin α，v2＝v0cs θ，xOB＝v22t＋ eq \f(1,2) a2（2t）2
小球在水平方向做匀速直线运动，C为OB中点，则x＝ eq \f(1,2) xOB
代入数据解得：x＝40 m
答案：（1）2 s （2）10 eq \r(3) m （3）40 m
10．解析：（1）在最低点3mg－mg＝m eq \f(v eq \\al(\s\up1(2),\s\d1(1)) ,\f(L,2))
绳子断后，两熊做平抛运动，则 eq \f(3,2) L＝ eq \f(1,2) gt eq \\al(\s\up1(2),\s\d1(1))
两熊落地点离O点的水平距离x1＝v1t1
联立可得x1＝ eq \r(3) L
（2）设绳长为d，则在最低点3mg－mg＝m eq \f(v eq \\al(\s\up1(2),\s\d1(2)) ,d)
绳子断后，两熊做平抛运动，则2L－d＝ eq \f(1,2) gt eq \\al(\s\up1(2),\s\d1(2))
两熊落地点离O点的水平距离x2＝v2t2
即x2＝2 eq \r(（2L－d）d)
则当d＝L时，两熊落地点离O点水平距离最远，此时最大值x2＝2L
（3）两熊做圆锥摆运动时，设绳子与竖直方向的夹角为θ时，绳子被拉断．
竖直方向3mg cs θ＝mg
水平方向3mg sin θ＝m eq \f(v eq \\al(\s\up1(2),\s\d1(3)) ,L sin θ)
此时两熊离地面的高度为h＝2L－L cs θ
此后两熊做平抛运动h＝ eq \f(1,2) gt eq \\al(\s\up1(2),\s\d1(3))
水平位移x3＝v3t3
由几何关系：落地点到O点的水平距离s＝ eq \r(（L sin θ）2＋x eq \\al(\s\up1(2),\s\d1(3)) )
联立可求得s＝ eq \f(2\r(22),3) L
答案：（1） eq \r(3) L （2）d＝L时 2L （3） eq \f(2\r(22),3) L