





高中物理高考 2022年高考物理一轮复习 第6章 专题强化9 动能定理在多过程问题中的应用课件PPT
展开1.会用动能定理解决多过程、多阶段的问题.2.掌握动能定理在往复运动问题中的应用.
NEIRONGSUOYIN
题型一 动能定理在多过程问题中的应用
题型二 动能定理在往复运动问题中的应用
1.运用动能定理解决多过程问题,有两种思路:(1)可分段应用动能定理求解;(2)全过程应用动能定理:所求解的问题不涉及中间的速度时,全过程应用动能定理求解更简便.2.全过程列式时,涉及重力、弹簧弹力、大小恒定的阻力或摩擦力做功时,要注意它们的特点.(1)重力、弹簧弹力做功取决于物体的初、末位置,与路径无关.(2)大小恒定的阻力或摩擦力做功的数值等于力的大小与路程的乘积.
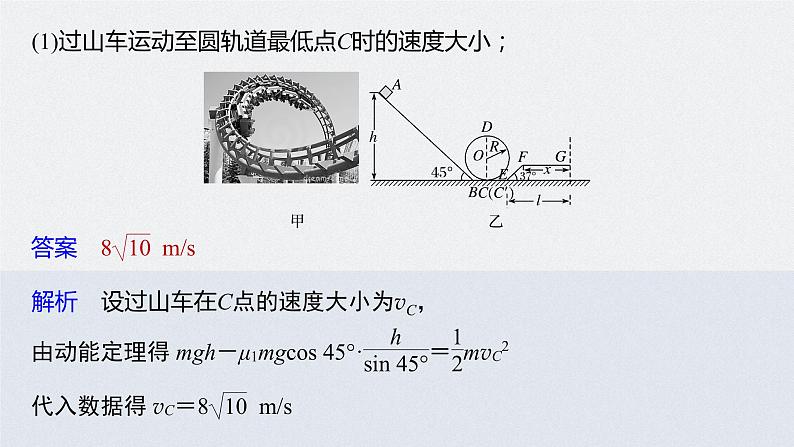
例1 (2016·浙江10月选考·20)如图1甲所示,游乐场的过山车可以底朝上在竖直圆轨道上运行,可抽象为图乙所示的模型.倾角为45°的直轨道AB、半径R=10 m的光滑竖直圆轨道和倾角为37°的直轨道EF,分别通过水平光滑衔接轨道BC、C′E平滑连接,另有水平减速直轨道FG与EF平滑连接,EG间的水平距离l=40 m.现有质量m=500 kg的过山车,从高h=40 m处的A点由静止下
滑,经BCDC′EF最终停在G点.过山车与轨道AB、EF间的动摩擦因数均为μ1=0.2,与减速直轨道FG间的动摩擦因数μ2=0.75.过山车可视为质点,运动中不脱离轨道,g取10 m/s2.求:
(1)过山车运动至圆轨道最低点C时的速度大小;
解析 设过山车在C点的速度大小为vC,
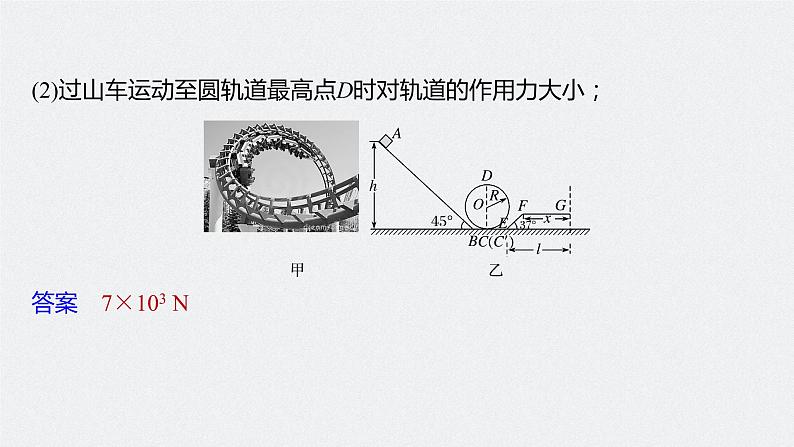
(2)过山车运动至圆轨道最高点D时对轨道的作用力大小;
答案 7×103 N
解析 设过山车在D点速度大小为vD,由动能定理得
由牛顿第三定律知,过山车在D点对轨道的作用力大小为7×103 N
(3)减速直轨道FG的长度x.(已知sin 37°=0.6,cs 37°=0.8)
解析 全程应用动能定理
1.(动能定理在多过程问题中的应用)(2020·河南信阳市罗山高三一模)如图2甲所示,一倾角为37°,长L=3.75 m的斜面AB上端和一个竖直圆弧形光滑轨道BC相连,斜面与圆轨道相切于B处,C为圆弧轨道的最高点.t=0时刻有一质量m=1 kg的物块沿斜面上滑,其在斜面上运动的v-t图象如图乙所示.已知圆轨道的半径R=0.5 m.(取g=10 m/s2,sin 37°=0.6,cs 37°=0.8)求:
(1)物块与斜面间的动摩擦因数μ;
解析 由题图乙可知物块上滑时的加速度大小为a=10 m/s2①根据牛顿第二定律有:mgsin 37°+μmgcs 37°=ma②由①②联立解得μ=0.5③
(2)物块到达C点时对轨道的压力的大小FN;
解析 设物块到达C点时的速度大小为vC,由动能定理得:
联立③④⑤解得:FN′=4 N ⑥根据牛顿第三定律得:FN=FN′=4 N ⑦物块在C点时对轨道的压力大小为4 N
(3)试通过计算分析是否可能存在物块以一定的初速度从A点滑上轨道,通过C点后恰好能落在A点.如果能,请计算出物块从A点滑出的初速度大小;如果不能请说明理由.
解析 设物块以初速度v1上滑,最后恰好落到A点物块从C到A,做平抛运动,
水平方向:Lcs 37°-Rsin 37°=vC′t ⑨
所以物块能通过C点落到A点物块从A到C,由动能定理得:
在有些问题中物体的运动过程具有重复性、往返性,而在这一过程中,描述运动的物理量多数是变化的,而且重复的次数又往往是无限的或者难以确定.求解这类问题时若运用牛顿运动定律及运动学公式将非常繁琐,甚至无法解出.由于动能定理只涉及物体的初、末状态而不计运动过程的细节,此类问题多涉及滑动摩擦力,或其他阻力做功,其做功的特点与路程有关,求路程对应的是摩擦力做功,所以用动能定理分析这类问题可使解题过程简化.
例2 如图3所示,竖直面内有一粗糙斜面AB,BCD部分是一个光滑的圆弧面,C为圆弧的最低点,AB正好是圆弧在B点的切线,圆心O与A、D点在同一高度,θ=37°,圆弧面的半径R=3.6 m,一滑块质量m=5 kg,与AB斜面间的动摩擦因数μ=0.45,将滑块从A点由静止释放(sin 37°=0.6,cs 37°=0.8,g取10 m/s2).求在此后的运动过程中:(1)滑块在AB段上运动的总路程;
解析 由题意可知斜面AB与水平面的夹角为θ=37°,知mgsin θ>μmgcs θ,故滑块最终不会停留在斜面上,由于滑块在AB段受摩擦力作用,则滑块做往复运动的高度将越来越低,最终以B点为最高点在光滑的圆弧面上往复运动.设滑块在AB段上运动的总路程为s,滑块在AB段上所受摩擦力大小Ff=μFN=μmgcs θ,从A点出发到最终以B点为最高点做往复运动,由动能定理得mgRcs θ-Ffs=0,
(2)在滑块运动过程中,C点受到的压力的最大值和最小值.
答案 102 N 70 N
解析 滑块第一次过C点时,速度最大,设为v1,分析受力知此时滑块所受轨道支持力最大,设为Fmax,
解得Fmax=102 N.滑块以B为最高点做往复运动的过程中过C点时,速度最小,设为v2,此时滑块所受轨道支持力最小,设为Fmin,从B到C,
解得Fmin=70 N,根据牛顿第三定律可知C点受到的压力最大值为102 N,最小值为70 N.
2.(动能定理在往复运动中的应用)(2020·浙江高三开学考试)如图4所示,有一圆弧形的槽ABC,槽底B放在水平地面上,槽的两侧A、C与光滑斜坡aa′、bb′分别相切,相切处a、b位于同一水平面内,距水平地面高度为h.一质量为m的小物块从斜坡aa′上距水平面ab的高度为2h处沿斜
坡自由滑下,并自a处进入槽内,到达b处后沿斜坡bb′向上滑行,到达的最高处距水平面ab的高度为h,若槽内的动摩擦因数处处相同,不考虑空气阻力,且重力加速度为g,则
A.小物块第一次从a处运动到b处的过程中克 服摩擦力做功mghB.小物块第一次经过B点时的动能等于2.5mghC.小物块第二次运动到a处时速度为零D.经过足够长的时间后,小物块最终一定停 在B处
解析 在第一次运动过程中,小物块克服摩擦力做功,根据动能定理可知mgh-Wf=0-0,解得Wf=mgh,故A正确;因为小物块从右侧到最低点的过程中对轨道的压力较大,所受的摩擦力较大,所以小物块从
右侧到最低点的过程中克服摩擦力做的功 ,设小物块第1次通过最低点的速度为v,从自由滑下到最低点的过程,由动能定理得3mgh-Wf1=Ek-0,解得Ek<2.5mgh,故B错误;
由于在AC段,小物块与轨道间有摩擦力,故小物块在某一位置的速度大小要减小,故与轨道间的摩擦力减小,第二次在AC段运动时克服摩擦力做功比第一次要少,故第二次到达a(A)点时,有一定的速度,故C错误;
由于在AC段存在摩擦力,故小物块在B点两侧某一位置可能处于静止状态,故D错误.
3.(动能定理在往复运动中的应用)(2019·河南郑州一中模拟)如图5所示,ABCD为一竖直平面内的轨道,其中BC水平,A点比BC高出H=10 m,BC长为l=1 m,AB和CD轨道光滑.一质量为m=1 kg的物体,从A点以v1=4 m/s的速度开始运动,经过BC后滑到高出C点h=10.3 m的D点时速度为零,求:(取g=10 m/s2)(1)物体与BC轨道间的动摩擦因数;
解析 分析从A点到D点的过程,由动能定理得
(2)物体第5次经过B点时的速度大小;
答案 13.3 m/s
解析 设物体第5次经过B点时的速度为v2,在此过程中物体在BC上滑动了4次,由动能定理得
(3)物体最后停止的位置(距B点).
解析 设物体运动的全过程在水平面上通过的路程为s,
解得s=21.6 m.所以物体在轨道上来回滑动了10次后,还有1.6 m,故距B点的距离s′=2 m-1.6 m=0.4 m.
1.(2021·海南高三月考)如图1所示,ABCD是一个盆式容器,盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧,BC水平,其长度d=0.50 m,盆边缘的高度为h=0.30 m.在A处放一个质量为m的小物块并让其由静止下滑.已知盆内侧壁是光滑的,而盆底BC面与小物块间的动摩擦因数为μ=0.10.小物块在盆内来回滑动,最后停下来,则停止的地点到B的距离为 m m D.0
解析 小物块从A点出发到最后停下来,设小物块在BC面上运动的总路程为s,整个过程由动能定理有:mgh-μmgs=0,
3.如图2所示,倾角为37°的粗糙斜面AB底端与半径R=0.4 m的光滑半圆轨道BC平滑相连,O为轨道圆心,BC为圆轨道直径且处于竖直方向,A、C两点等高.质量m=1 kg的滑块(可视为质点)从A点由静止开始下滑,恰能滑到与O等高的D点,g取10 m/s2,sin 37°=0.6,cs 37°=0.8.(1)求滑块与斜面间的动摩擦因数μ;
解析 滑块由A到D的过程,根据动能定理,
(2)若使滑块能到达C点,求滑块从A点沿斜面滑下时的初速度的最小值;
解析 滑块恰能到达C点时,初速度最小,
(3)若滑块离开C点时的速度大小为4 m/s,求滑块从C点飞出至落到斜面上的时间t.
解析 滑块离开C点做平抛运动,
联立得5t2+3t-0.8=0,解得t=0.2 s.
4.(2020·广东中山纪念中学月考)如图3所示,AB是倾角为θ=30°的粗糙直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R.一个质量为m的物体(可以看成质点)从直轨道上的P点由静止释放,结果它能在两轨道间做往返运动.已知P点与圆弧的圆心O等高,物体做往返运动的整个过程中在AB轨道上通过的路程为s.求:(1)物体与轨道AB间的动摩擦因数μ;
解析 由题意可知,物体最终以B点为最高点在圆弧面内做往返运动,对整个过程由动能定理得mgRcs θ-μmgscs θ=0,
(2)最终当物体通过圆弧轨道最低点E时,对圆弧轨道的压力的大小;
解析 最终物体以B点为最高点,在圆弧底部做往复运动,对从B到E过程,由动能定理得
(3)为使物体能顺利到达圆弧轨道的最高点D,释放点距B点的距离L′至少多大.
5.(2020·吉林长春市第二实验中学开学考试)如图4所示,让摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,小球在粗糙的水平面上由D点向右做匀减速运动,到达A孔进入半径R=0.3 m的竖直放置的光滑圆弧轨道,当摆球进入圆轨道立即关闭A孔.已知摆线长L= 2 m,θ=53°,小球质量为m=0.5 kg,D点与A孔的水平距离s=2 m,g取10 m/s2.(sin 53°=0.8,cs 53°=0.6)(1)求摆线能承受的最大拉力为多大;
解析 当摆球由C到D运动,
可得Fm=1.8mg=9 N
(2)要使摆球能进入圆轨道并且不脱离轨道,求摆球与粗糙水平面间的动摩擦因数μ的范围.
答案 2.5≤μ≤0.4或者μ≤0.025
解析 小球不脱离圆轨道分两种情况①要保证小球能到达A孔,设小球到达A孔的速度恰好为零,由动能定理可得
可得μ1=0.4若进入A孔的速度较小,那么将会在圆心以下做往返运动,不脱离轨道,其临界情况为到达圆心等高处速度为零,
可求得μ2=0.25②若小球能过圆轨道的最高点则不会脱离轨道,当小球恰好到达最高点时,在圆周的最高点,由牛顿第二定律可得
解得μ3=0.025综上所述,动摩擦因数μ的范围为0.25≤μ≤0.4或者μ≤0.025.
6.如图5所示,在地面上竖直固定了刻度尺和轻质弹簧,弹簧原长时上端与刻度尺上的A点等高.质量m=0.5 kg的篮球静止在弹簧正上方,其底端距A点的高度h1=1.10 m,篮球静止释放,测得第一次撞击弹簧时,弹簧的最大形变量x1=0.15 m,第一次反弹至最高点,篮球底端距A点的高度h2=0.873 m,篮球多次反弹后静止在弹簧的上端,此时弹簧的形变量x2=0.01 m,弹性势能为Ep=0.025 J.若篮球运动时受到的空气阻力大小恒定,忽略篮球与弹簧碰撞时的能量损失和篮球形变,弹簧形变在弹性限度范围内,g取10 m/s2.求:
(1)弹簧的劲度系数;
答案 500 N/m
解析 由最后静止的位置可知kx2=mg,所以k=500 N/m
(2)篮球在运动过程中受到的空气阻力大小;
解析 由动能定理可知,在篮球由静止下落到第一次反弹至最高点的过程中
整个过程动能变化为0,重力做功mgΔh=mg(h1-h2)=1.135 J空气阻力恒定,作用距离为L=h1+h2+2x1=2.273 m解得Ff≈0.5 N
(3)篮球在整个运动过程中通过的路程;
解析 整个运动过程中,空气阻力一直与运动方向相反
整个过程动能变化为0,重力做功W=mgΔh′=mg(h1+x2)=5.55 J弹力做功W弹=-Ep=-0.025 J则空气阻力做功Wf=-Ffs=-5.525 J解得s=11.05 m.
(4)篮球在整个运动过程中速度最大的位置.
答案 第一次下落至A点下方0.009 m处速度最大
解析 篮球速度最大的位置是第一次下落到合力为零的位置,此时mg=Ff+kx3,得x3=0.009 m,即篮球第一次下落至A点下方0.009 m处速度最大.
新高考物理一轮复习精品课件第6章专题强化9动能定理在多过程问题中的应用(含解析): 这是一份新高考物理一轮复习精品课件第6章专题强化9动能定理在多过程问题中的应用(含解析),共49页。PPT课件主要包含了内容索引,课时精练,题型一,答案09m,答案7×103N,答案30m,全程应用动能定理,题型二,答案8m,答案145N等内容,欢迎下载使用。
高考物理一轮复习课件+讲义 第6章 专题强化9 动能定理在多过程问题中的应用: 这是一份高考物理一轮复习课件+讲义 第6章 专题强化9 动能定理在多过程问题中的应用,文件包含高考物理一轮复习第6章专题强化9动能定理在多过程问题中的应用pptx、高考物理一轮复习第6章专题强化9动能定理在多过程问题中的应用docx等2份课件配套教学资源,其中PPT共58页, 欢迎下载使用。
新高考物理一轮复习课件 第6章 专题强化9 动能定理在多过程问题中的应用: 这是一份新高考物理一轮复习课件 第6章 专题强化9 动能定理在多过程问题中的应用,共52页。PPT课件主要包含了高考物理一轮复习策略,第六章机械能,内容索引,课时精练等内容,欢迎下载使用。












