



第15讲 平面直角坐标系规律题(原卷版+解析)
展开第15讲 平面直角坐标系规律题
【类题训练】
1.如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(4,0),F(﹣4,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以4个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2022次相遇地点的坐标是( )
A.(2,﹣2) B.(﹣2,﹣2) C.(﹣2,2) D.(2,2)
【分析】利用行程问题中的相遇问题,由于矩形的边长为8和4,物体甲是物体乙的速度的2倍,求得每一次相遇的地点,找出规律即可解答.
【解答】解:由题意知:矩形的边长为8和4,
①第一次相遇物体甲与物体乙运动的时间为(2+4+4+2)÷(4+2)=2(秒),
∴第一次相遇地点的坐标是(﹣2,2);
②第二次相遇物体甲与物体乙运动的时间为(8×2+4×2)÷(4+2)=4(秒),
∴第二次相遇地点的坐标是(4,0);
③第三次相遇地点的坐标是(﹣2,﹣2);
④第四次相遇地点的坐标是(﹣2,2);
…
则每相遇三次,为一个循环,
∵2022÷3=674,
故两个物体运动后的第2022次相遇地点的坐标为:(﹣2,﹣2),
故答案为:B.
2.如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3)……,则第50个点的坐标为( )
A.(7,6) B.(8,8) C.(9,6) D.(10,5)
【分析】设横坐标为n的点的个数为an,横坐标≤n的点的个数为Sn(n为正整数),结合图形找出部分an的值,根据数值的变化找出变化规律“an=n”,再罗列出部分Sn的值,根据数值的变化找出变化规律“Sn=”,依次变化规律解不等式100≤即可得出结论.
【解答】解:设横坐标为n的点的个数为an,横坐标≤n的点的个数为Sn(n为正整数),
观察,发现规律:a1=1,a2=2,a3=3,…,
∴an=n.
S1=a1=1,S2=a1+a2=3,S3=a1+a2+a3=6,…,
∴Sn=1+2+…+n=.
当50≤Sn,即50≤,
解得:n≤﹣(舍去),或n≥.
∵9<<10,
则第50个点的横坐标为10.
故选:D.
3.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角(∠AOM=∠BOM),当点P第2022次碰到矩形的边时,点P的坐标为( )
A.(0,3) B.(5,0) C.(1,4) D.(8,3)
【分析】动点的反弹与光的反射入射是一个道理,根据反射角与入射角的定义可以在格点中作出图形,可以发现,在经过6次反射后,动点回到起始的位置,将2019除以6得到336,且余数为3,说明点P第2022次碰到矩形的边时为第336个循环组的第6次反弹,因此点P的坐标为(0,3).
【解答】解:如图,根据反射角与入射角的定义作出图形,
解:如图,第6次反弹时回到出发点,
∴每6次碰到矩形的边为一个循环组依次循环,
∵2022÷6=337,
∴点P第2022次碰到矩形的边时是第336个循环组的第6次碰边,
坐标为(0,3).
故选:A.
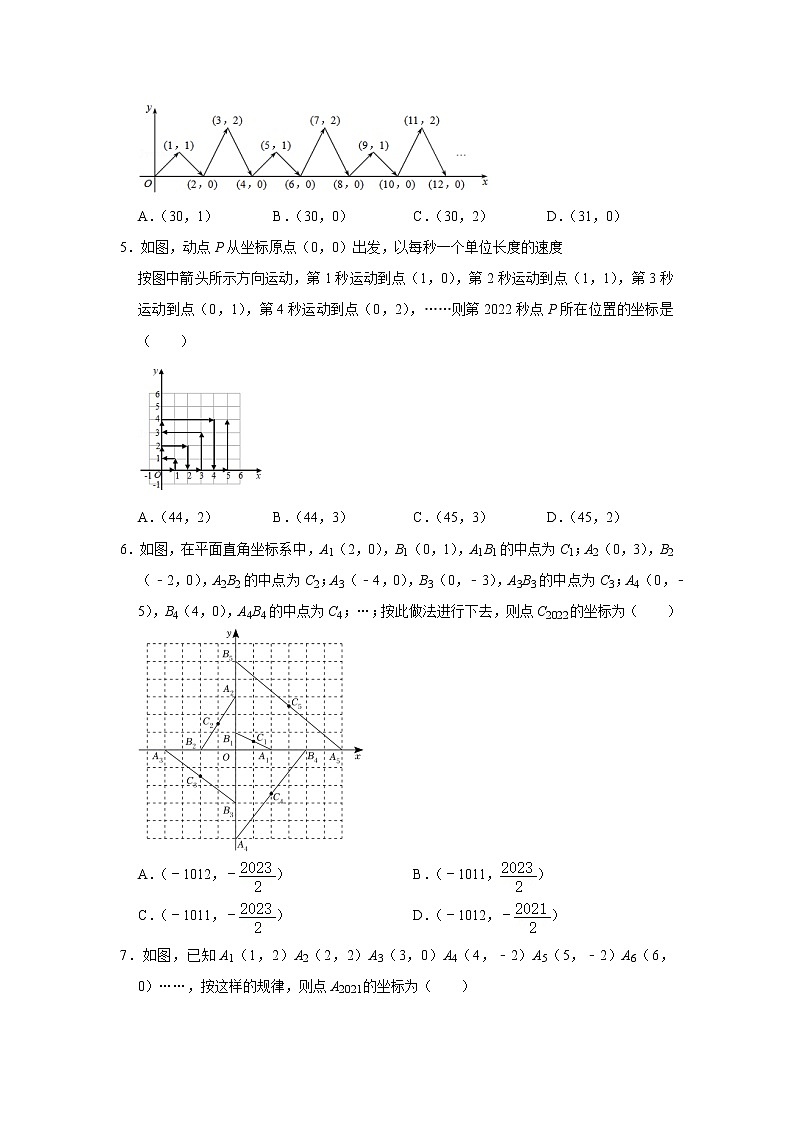
4.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第30次运动后,动点P的坐标是( )
A.(30,1) B.(30,0) C.(30,2) D.(31,0)
【分析】观察点的坐标变化发现每个点的横坐标与次数相等,纵坐标是1,0,2,0,…4个数一个循环,进而可得经过第30次运动后,动点P的坐标.
【解答】解:观察点的坐标变化可知:
第1次从原点运动到点(1,1),
第2次接着运动到点(2,0),
第3次接着运动到点(3,2),
第4次接着运动到点(4,0),
第5次接着运动到点(5,1),
…
按这样的运动规律,
发现每个点的横坐标与次数相等,
纵坐标是1,0,2,0,4个数一个循环,
因为30÷4=7……2,
所以经过第30次运动后,
动点P的坐标是(30,0).
故选:B.
5.如图,动点P从坐标原点(0,0)出发,以每秒一个单位长度的速度
按图中箭头所示方向运动,第1秒运动到点(1,0),第2秒运动到点(1,1),第3秒运动到点(0,1),第4秒运动到点(0,2),……则第2022秒点P所在位置的坐标是( )
A.(44,2) B.(44,3) C.(45,3) D.(45,2)
【分析】分析点P在坐标系中的运动路线,寻找点P运动至x轴或y轴时的点坐标的规律.
【解答】解:根据题意列出P的坐标寻找规律.
P1(1,0);
P8(2,0);
P9(3,0);
P24(4,0);
P48(6,0);
即P2n(2n+2)坐标为(2n,0).
P2024(44,0).
∴P2022坐标为P2024(44,0)退回两个单位→(44,1)→(44,2).
故选:A.
6.如图,在平面直角坐标系中,A1(2,0),B1(0,1),A1B1的中点为C1;A2(0,3),B2(﹣2,0),A2B2的中点为C2;A3(﹣4,0),B3(0,﹣3),A3B3的中点为C3;A4(0,﹣5),B4(4,0),A4B4的中点为C4;…;按此做法进行下去,则点C2022的坐标为( )
A.(﹣1012,﹣) B.(﹣1011,)
C.(﹣1011,﹣) D.(﹣1012,﹣)
【分析】根据题意得点∁n的位置按4次一周期的规律循环出现,可求得点C2022在第二象限,从而可求得该题结果.
【解答】解:由题意可得,点∁n的位置按4次一周期的规律循环出现,
∵2022÷4=505……2,
∴点C2022在第二象限,
∵位于第二象限内的点C2的坐标为(﹣1,),
点C6的坐标为(﹣3,),
点C10的坐标为(﹣5,),
……
∴点∁n的坐标为(﹣,),
∴当n=2022时,﹣=﹣=﹣1011,==,
∴点C2022的坐标为(﹣1011,),
故选:B.
7.如图,已知A1(1,2)A2(2,2)A3(3,0)A4(4,﹣2)A5(5,﹣2)A6(6,0)……,按这样的规律,则点A2021的坐标为( )
A.(2021,2) B.(2020,2) C.(2021,﹣2) D.2020,﹣2)
【分析】观察发现,每6个点形成一个循环,再根据点A6的坐标及2021÷6所得的整数及余数,可计算出点A2021的横坐标,再根据余数对比第一组的相应位置的数可得其纵坐标.
【解答】解:观察发现,每6个点形成一个循环,
∵A6(6,0),
∴OA6=6,
∵2021÷6=336…5,
∴点A2021的位于第337个循环组的第5个,
∴点A2021的横坐标为6×336+5=2021,其纵坐标为:﹣2,
∴点A2021的坐标为(2021,﹣2).
故选:C.
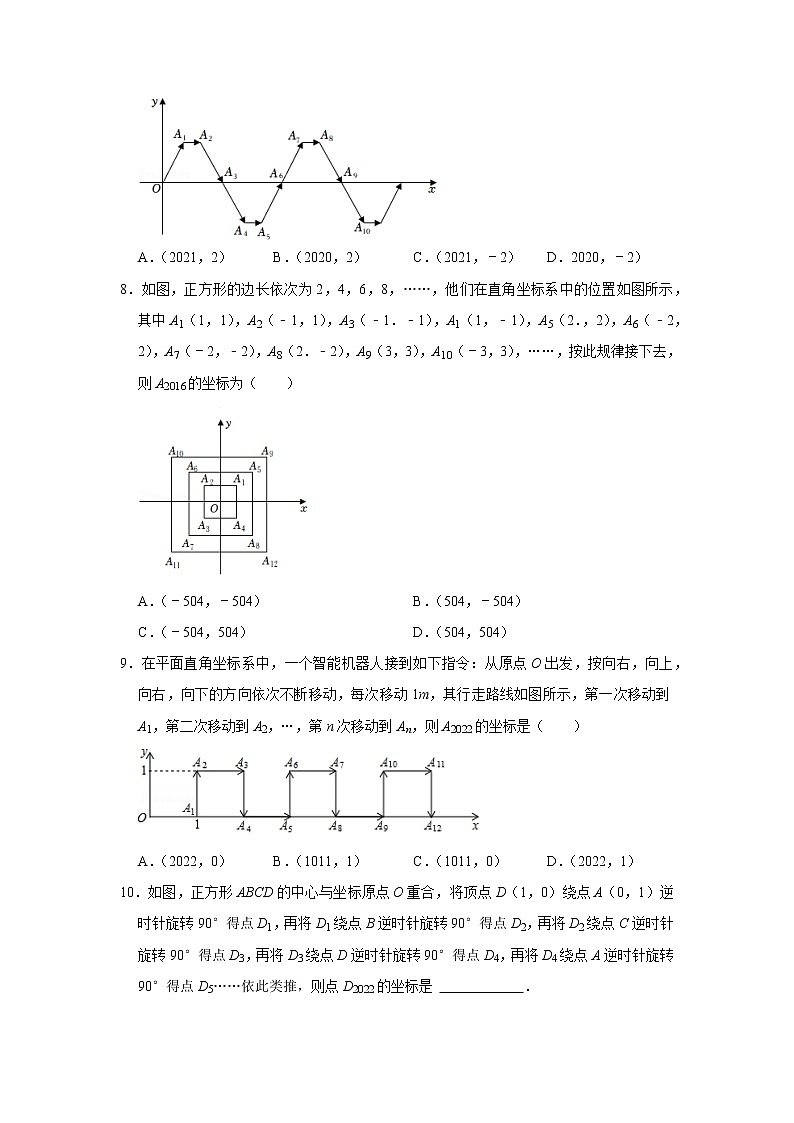
8.如图,正方形的边长依次为2,4,6,8,……,他们在直角坐标系中的位置如图所示,其中A1(1,1),A2(﹣1,1),A3(﹣1.﹣1),A1(1,﹣1),A5(2.,2),A6(﹣2,2),A7(﹣2,﹣2),A8(2.﹣2),A9(3,3),A10(﹣3,3),……,按此规律接下去,则A2016的坐标为( )
A.(﹣504,﹣504) B.(504,﹣504)
C.(﹣504,504) D.(504,504)
【分析】由正方形的中心都是位于原点,边长依次为2,4,6,8,…,可得第n个正方形的顶点横坐标与纵坐标的绝对值都是n.计算2016÷4,根据商和余数知道是第几个正方形的顶点,且在哪一个象限,进而得出A2016的坐标.
【解答】解:∵2016÷4=504,
∴顶点A2016是第504个正方形的顶点,且在第二象限,
横坐标是﹣504,纵坐标是504,
∴A2016(﹣504,504),
故选:C.
9.在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第一次移动到A1,第二次移动到A2,…,第n次移动到An,则A2022的坐标是( )
A.(2022,0) B.(1011,1) C.(1011,0) D.(2022,1)
【分析】根据图象可得移动4次完成一个循环,从而可得出点A2022的坐标.
【解答】解:A1(1,0),A2(1,1),A3(2,1),A4(2,0),A5(3,0),A6(3,1),…,
2022÷4=505……2,
所以A2022的坐标为(505×2+1,1),
则A2021的坐标是(1011,1).
故选:B.
10.如图,正方形ABCD的中心与坐标原点O重合,将顶点D(1,0)绕点A(0,1)逆时针旋转90°得点D1,再将D1绕点B逆时针旋转90°得点D2,再将D2绕点C逆时针旋转90°得点D3,再将D3绕点D逆时针旋转90°得点D4,再将D4绕点A逆时针旋转90°得点D5……依此类推,则点D2022的坐标是 .
【分析】由题意观察发现:每四个点一个循环,D4n+2(﹣4n﹣3,4n+2),由2022=505×4+2,推出D2022(﹣2023,2022).
【解答】解:∵将顶点D(1,0)绕点A(0,1)逆时针旋转90°得点D1,
∴D1(1,2),
∵再将D1绕点B逆时针旋转90°得点D2,再将D2绕点C逆时针旋转90°得点D3,再将D3绕点D逆时针旋转90°得点D4,再将D4绕点A逆时针旋转90°得点D5……
∴D2(﹣3,2),D3(﹣3,﹣4),D4(5,﹣4),D5(5,6),D6(﹣7,6),……,
观察发现:每四个点一个循环,D4n+2(﹣4n﹣3,4n+2),
∵2022=4×505+2,
∴D2022(﹣2023,2022);
故答案为:(﹣2023,2022).
11.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,﹣1)…,根据这个规律探索可得,第10个点的坐标为 ,第55个点的坐标为 .
【分析】从图中可以看出横坐标为1的有一个点,横坐标为2的有2个点,横坐标为3的有3个点,…依此类推横坐标为n的有n个点.题目要求写出第10个点和第55个点的坐标,我们可以通过加法计算算出第10个点和第50个点分别位于第几列第几行,然后对应得出坐标规律,将行列数代入规律式.
【解答】解:在横坐标上,第一列有一个点,第二列有2个点…第n个有n个点,
并且奇数列点数对称而偶数列点数y轴上方比下方多一个,
∵1+2+3+4=10,1+2+3+…+10=55,
∴第10个点在第4列自下而上第4行,
所以奇数列的坐标为(n,)(n,﹣1)…(n,);
偶数列的坐标为(n,)(n,﹣1)…(n,1﹣),
由加法推算可得到第55个点位于第10列自下而上第10行.
代入上式得第10个点的坐标为(4,2),第55个点的坐标为(10,5),
故答案为:(4,2),(10,5).
12.如图,在平面直角坐标系中,AB∥EG∥x轴,BC∥DE∥HG∥AP∥y轴,点D,C,P,H在x轴上,A(1,2),B(﹣1,2),D(﹣3,0),E(﹣3,﹣2),G(3,﹣2).
(1)若点M在线段EG上,当点M与点A的距离最小时,点M的坐标为 ;
(2)把一条长为2022个单位长度且无弹性的细线(粗细忽略不计)的一端固定在A处,并按AB→C→D→E→F→G→H→P→A…的规律紧绕在图形“凸”的边上,则细线的另一端所在位置的点的坐标为 .
【分析】(1)根据“垂线段最短”可确定点M的坐标;
(2)先计算出该图形的周长是20,再由2022÷20的计算结果确定此题结果.
【解答】解:(1)由垂线段最短可得,
当AM⊥EG时点M与点A的距离最小,
由题意得此时M的坐标为(1,﹣2),
故答案为:(1,﹣2);
(2)由题意得,此图形的周长为:
2×[3﹣(﹣3)+2﹣(﹣2)]
=2×(6+4)
=2×10
=20,
∵2022÷20=101……2,
∴细线的另一端在点B的位置,
即另一端所在位置的点的坐标为(﹣1,2),
故答案为:(﹣1,﹣2).
13.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…按这样的规律第13次运动到点的坐标 ;经过第2022次运动后,动点P的坐标 .
【分析】由题意可得点P的运动按4次一周期的规律循环出现,再根据计算2022÷4=5…2可得此题结果.
【解答】解:由题意可得,点P第n次运动后的横坐标为n,纵坐标按1,0,2,0,1,…4次一周期的规律循环出现,
∵13÷4=3•••1,2022÷4=5…2,
∴第13次运动到点的坐标(13,1);经过第2022次运动后,动点P的坐标是(2022,0),
故答案为:(13,1),(2022,0).
14.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)…根据这个规律探究可得,第22个点的坐标为 .
【分析】观察图形,可知:每列的个数成等差数列,由等差数列的求和公式可得出第22个点为第7列的由上往下第1个,可求出第22个点的坐标(此处纵坐标为6﹣1).
【解答】解:观察图形,可知:每列的个数成等差数列.
∵1+2+3+4+5+6=21,
∴第22个点为第7列从上往下的第1个.
∴第22个点的坐标为(7,6).
故答案为:(7,6).
15.如图,在平面直角坐标系中,点A1在x轴的正半轴上,且OA1=1,以点A1为直角顶点,逆时针方向作Rt△A1OA2,使A1A2=OA1;再以点A2为直角顶点,逆时针方向作Rt△A2OA3,使A2A3=OA2;再以点A3为直角顶点,逆时针方向作Rt△A3OA4,使A3A4=OA3;依次进行作下去,则点A2022的坐标为 .
【分析】本题点A坐标变化规律要分别从旋转次数与点A所在象限或坐标轴、点A到原点的距离与旋转次数的对应关系.
【解答】解:由已知,点A每次旋转转动45°,则转动一周需转动8次,每次转动点A到原点的距离变为转动前的倍,
∵2022=252×8+6,
根据规律OAn=()n﹣1,
∴OA2022=()2021,
∴点A2022的在第三象限的角平分线上,
∴点A2022的横坐标为:﹣()2021÷=﹣()2020=﹣21010,
点A2022的纵坐标为:﹣()2021÷=﹣()2020=﹣21010
∴点A2022的坐标为(﹣21010,﹣21010),
故答案为:(﹣21010,﹣21010).
16.在平面直角坐标系中,﹣蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.
(1)填写下列各点的坐标:A4( , ),A8( , );
(2)写出点A4n的坐标(n是正整数)A4n( , );
(3)求出A2022的坐标.
【分析】根据题意可直接找出点的坐标规律,A4n( 2n,0),A4n+1( 2n,1),A4n+2( 2n+1,1),A4n+3( 2n+1,0),根据规律直接求出A4( 2,0),A8( 4,0),A4n( 2n,0)A2022( 1012,1).
【解答】解:观察图形可知,A1( 0,1),A2( 1,1),A3( 1,0),A4( 2,0),A5( 2,1),A6( 3,1),...,A4n( 2n,0),A4n+1( 2n,1),A4n+2( 2n+1,1),A4n+3( 2n+1,0),
(1)根据题意,可直接读出A4( 2,0),A8( 4,0),
故答案为:2,0,4,0;
(2)根据点的坐标规律可知,A4n( 2n,0),
故答案为:2n,0;
(3)∵2022=4×505+2,
∴A2022( 1011,1).
17.对于任何实数a,可用[a]表示不超过a的最大整数,即整数部分,{a}表示a的小数部分.例如:[1.3]=1,{﹣2.6}=0.4.
(1)[]= ,{﹣}= ;
(2)在平面直角坐标系中,有一序列点P1([1],{1}),P2([],{}),P3([],{}),P4([2],{2}),P5([],{}),…
请根据这个规律解决下列问题:
①点P10的坐标是 ;
②横坐标为10的点共有 个;
③在前2022个点中,纵坐标相等的点共有 个,并求出这些点的横坐标之和.
【分析】(1)根据题意直接求解即可;
(2)①根据题意找出点Pn的坐标为Pn([],{}),然后再求出点P10的坐标即可;
②根据[]=10,可推出100≤n<121,再找出其中的整数即可;
③将前几个点的坐标求出,找出规律:当n的值为平方数时,纵坐标为0,只有纵坐标为0时的点的纵坐标相等,再根据44<<45进行求解即可.
【解答】解:(1)∵1<2<4,
∴1<<2,
∴[]=1,
∵﹣4<﹣3<﹣1,
∴﹣2<﹣<﹣1,
∴{﹣}=﹣﹣(﹣2)=2﹣,
故答案为:1,2﹣;
(2)∵P1([1],{1}),P2([],{}),P3([],{}),P4([2],{2}),P5([],{}),…
∴可发现点Pn的坐标为Pn([],{}),
①根据规律可知,点P10的坐标为([],{}),
∵9<10<16,
∴3<<4,
∴[]=3,{}=﹣3,
∴点P10的坐标是(3,﹣3),
故答案为:(3,﹣3);
②∵点Pn的坐标为Pn([],{}),
∴当[]=10时,100≤n<121,其中的整数共21个,
故答案为:21;
③根据题意可得,P1(1,0),P2(1,﹣1),P3(1,﹣1),P4(2,0),P5(2,﹣2),P6(2,﹣2),P7(2,﹣2),P8(2,2﹣2),P9(3,0),P10(3,﹣3),…
可以发现,当n的值为平方数时,纵坐标为0,只有纵坐标为0时的点的纵坐标相等,
∵44<<45,
∴在前2022个点中,纵坐标相等的点共有44个,这些点的横坐标之和为1+2+3+...+44=990,
∴在前2022个点中,纵坐标相等的点共有44个,这些点的横坐标之和为990,
故答案为:44.
18.在平面直角坐标系中,乙蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动一个单位,其行走路线如图所示.
(1)填写下列各点的坐标:A4( );A8( );A12( )
(2)指出蚂蚁从点A100到A101的移动方向.
【分析】(1)观察图形可知,A4,A8、A12都在x轴上,求出OA4、OA8、OA12的长度,然后写出坐标即可;
(2)根据100是4的倍数,可知从点A100到A101的移动方向与从点O到A1的方向一致.
【解答】解:(1)由图可知,A4,A8、A12都在x轴上,
∵小蚂蚁每次移动1个单位,
∴OA4=2,OA8=4,OA12=6,
∴A4(2,0),A8(4,0),A12(6,0)
(2))∵100÷4=25,
∴100是4的倍数,
∴从点A100到A101的移动方向与从点O到A1的方向一致,为↑.
故答案为:2,0;4,0; 6,0.
19.如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将OA2B2变换成△OA3B3;已知变换过程中各点坐标分别为A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标为 ,B4的坐标为 .
(2)按以上规律将△OAB进行n次变换得到△OAnBn,则An的坐标为 ,Bn的坐标为 ;
(3)△OAnBn的面积为 .
【分析】(1)根据题目中的信息可以发现A1、A2、A3各点坐标的关系为横坐标是2n,纵坐标都是3,故可求得A4的坐标;B1、B2、B3各点的坐标的关系为横坐标是2n+1,纵坐标都为0,从而可求得点B4的坐标.
(2)根据(1)中发现的规律可以求得An、Bn点的坐标;
(3)依据An、Bn点的坐标,利用三角形面积计算公式,即可得到结论.
【解答】解:(1)∵A1(2,3)、A2(4,3)、A3(8,3).
∴A4的横坐标为:24=16,纵坐标为:3.
故点A4的坐标为:(16,3).
又∵B1(4,0)、B2(8,0)、B3(16,0).
∴B4的横坐标为:25=32,纵坐标为:0.
故点B4的坐标为:(32,0).
故答案为:(16,3),(32,0).
(2)由A1(2,3)、A2(4,3)、A3(8,3),可以发现它们各点坐标的关系为横坐标是2n,纵坐标都是3.
故An的坐标为:(2n,3).
由B1(4,0)、B2(8,0)、B3(16,0),可以发现它们各点坐标的关系为横坐标是2n+1,纵坐标都是0.
故Bn的坐标为:(2n+1,0);
故答案为:(2n,3),(2n+1,0);
(3)∵An的坐标为:(2n,3),Bn的坐标为:(2n+1,0),
∴△OAnBn的面积为×2n+1×3=3×2n.
第01讲 平面直角坐标系(原卷版讲义): 这是一份第01讲 平面直角坐标系(原卷版讲义),共9页。试卷主要包含了点的坐标,坐标确定位置,坐标与图形性质,方向角,坐标与图形变化-平移,将点平移到点处,正确的移法是等内容,欢迎下载使用。
人教版七年级数学下册压轴题专项讲练专题7.1平面直角坐标系中的规律问题(原卷版+解析): 这是一份人教版七年级数学下册压轴题专项讲练专题7.1平面直角坐标系中的规律问题(原卷版+解析),共30页。
初中数学人教版七年级下册7.1.2平面直角坐标系课时练习: 这是一份初中数学人教版七年级下册<a href="/sx/tb_c102671_t7/?tag_id=28" target="_blank">7.1.2平面直角坐标系课时练习</a>,共39页。












