第20讲等腰三角形（导学案+教案+精炼）

第20讲 等腰三角形

一、知识梳理

等腰三角形的概念与性质

等腰三角形的判定

等边三角形

线段的垂直平分线

二、题型、技巧归纳

考点1等腰三角形的性质的运用

例1如图在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠GDF＝∠ADF.

(1)求证：△ADE≌△BFE；

(2)连接EG，判断EG与DF的位置关系，

并说明理由．

技巧归纳：

(1)利用线段的垂直平分线进行等线段转换，进而进行角度转换．(2)在同一个三角形中，等角对等边与等边对等角进行互相转换．

考点2等腰三角形判定

例2、已知：如图锐角△ABC的两条高BD、CE相交于点O，且OB＝OC.

(1)求证：△ABC是等腰三角形；

(2)判断点O是否在∠BAC的平分线上，并说明理由．

技巧归纳：要证明一个三角形是等腰三角形，必须得到两边相等，而得到两边相等的方法主要有(1)通过等角对等边得两边相等；(2)通过三角形全等得两边相等；(3)利用垂直平分线的性质得两边相等．

考点3等腰三角形的多解问题

例3  已知等腰△ABC中，AD⊥BC于点D，且AD＝0.5  BC，则△ABC底角的度数为(　　)

A．45°              B．75°

C．45°或75°  D．60°

技巧归纳：因为等腰三角形的边有腰与底之分，角有底角和顶角之分，等腰三角形的高线要考虑高在形内和形外两种情况．故当题中条件给出不明确时，要分类讨论进行解题，才能避免漏解情况．

考点4等边三角形的判定与性质

例4   数学课上，李老师出示了如下框中的题目．在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED＝EC，如图试确定线段AE与DB的大小关系，并说明理由．

小敏与同桌小聪讨论后，进行了如下解答：

(1)特殊情况，探索结论

当点E为AB的中点时，如图20－4①，确定线段AE与DB的大小关系，请你直接写出结论：

AE________DB(填“>”“<”或“＝”)

（1）                        （2）

(2)特例启发，解答题目

解：题目中，AE与DB的大小关系是：AE________DB(填“>”“<”或“＝”)．理由如下：如图20－4②，过点E作EF∥BC，交AC于点F.

(请你完成以下解答过程)

(3)拓展结论，设计新题

在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED＝EC.若△ABC的边长为1，AE＝2，求CD的长(请你直接写出结果)．

技巧归纳：等边三角形中隐含着三边相等和三个角都等于60°的结论，所以要充分利用这些隐含条件，证明全等或者构造全等．

三、随堂检测

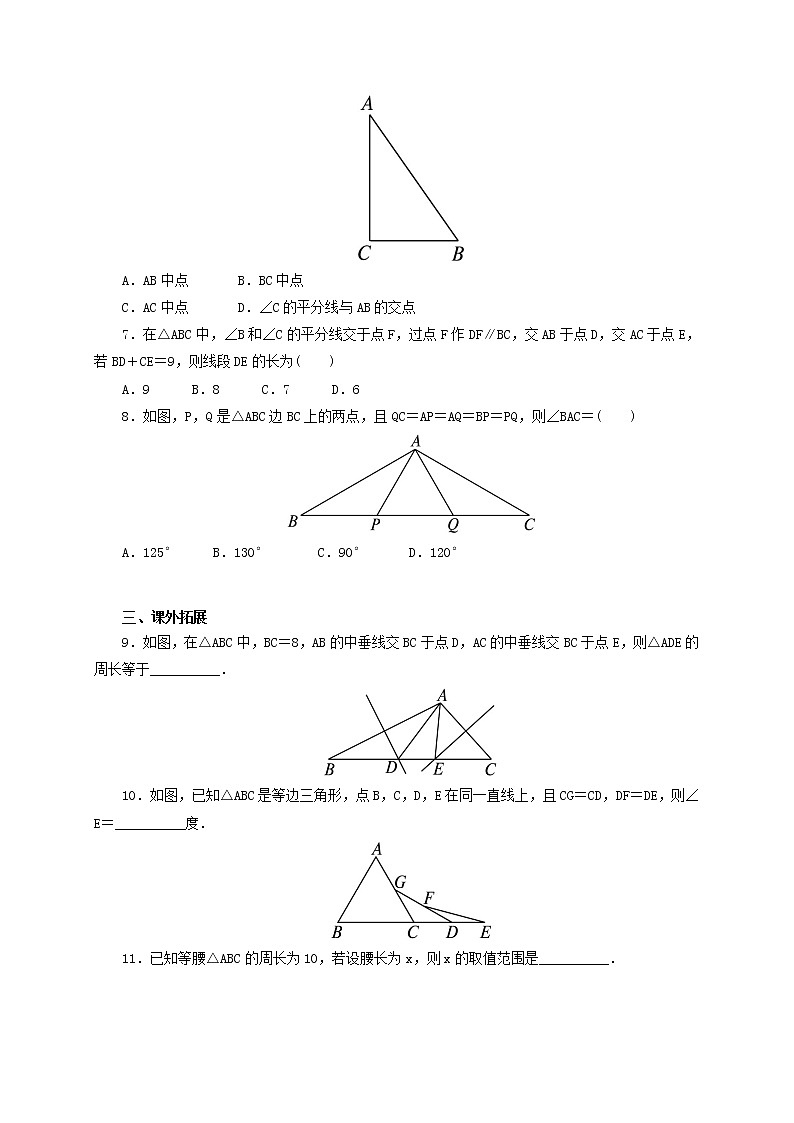
1.如图，已知△ABC是等边三角形，点B，C，D，E在同一直线上，且CG=CD，DF=DE，则∠E=　　　　度.

2.如图，将等边△ABC绕顶点A顺时针方向旋转，使边AB与AC重

合得△ACD，BC的中点E的对应点为F，则∠EAF的度数是　　　　.

3.如图，在△ABC中，AB=AC，∠A=120°，BC=6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为　(　　)

A.4 cm  B.3 cm  C.2 cm  D.1 cm

4.如图，等腰△ABC中，AB=AC，∠DBC=15°，AB的垂直平分线MN交AC于点D，则∠A的度数是　　　.

5.如图，△ABC中，∠C=90°，∠A=30°.

(1)用尺规作图作AB边上的中垂线DE，交AC于点D，交AB于点E.(保留作图痕迹，不要求写作法和证明).

(2)连接BD，求证：BD平分∠CBA.

参考答案

例1、解： (1)证明：∵AD∥BC，

∴∠ADE＝∠BFE，∠DAE＝∠FBE.

∵E是AB的中点，

∴AE＝BE.

∴△ADE≌△BFE.

(2)EG与DF的位置关系是EG⊥DF.

∵∠GDF＝∠ADF，

又∵∠ADE＝∠BFE，

∴∠GDF＝∠BFE，

∴GD＝GF.

由(1)得，DE＝EF，

∴EG⊥DF.

例2、解：(1)证明：∵OB＝OC，∴∠OBC＝∠OCB.

∵BD、CE是两条高，∴∠BDC＝∠CEB＝90°.

又∵BC＝CB，∴△BDC≌△CEB (AAS)．

∴∠DBC＝∠ECB, ∴AB＝AC.

∴△ABC是等腰三角形．

(2)点O是在∠BAC的平分线上．

连接AO.

∵△BDC≌△CEB，∴DC＝EB.

∵OB＝OC，∴ OD＝OE.

又∵∠BDC＝∠CEB＝90°，AO＝AO，

∴△ADO≌△AEO(HL)．

∴∠DAO＝∠EAO. ∴点O是在∠BAC的平分线上．

例3、

如图(1)：AB＝AC，

∵AD⊥BC，∴BD＝CD＝BC，∠ADB＝90°.

∵AD＝BC，∴AD＝BD，∴∠B＝45°，

即此时△ABC底角的度数为45°；

如图(2)，AC＝BC，

∵AD⊥BC，∴∠ADC＝90°.

∵AD＝BC，∴AD＝AC，∴∠C＝30°.

∴∠CAB＝∠B＝＝75°，

即此时△ABC底角的度数为75°.

综上，△ABC底角的度数为45°或75°.

故选C.

例4、（1）=

（2）=

方法一：等边三角形ABC中，

∠ABC＝∠ACB＝∠BAC＝60°，

AB＝BC＝AC.

∵EF∥BC，

∴∠AEF＝∠AFE＝60°＝∠BAC，

∴△AEF是等边三角形，∴AE＝AF＝EF，

∴AB－AE＝AC－AF，即BE＝CF.

又∵∠ABC＝∠EDB＋∠BED＝60°，

∠ACB＝∠ECB＋∠FCE＝60°，

且ED＝EC，

∴∠EDB＝∠ECB，∴∠BED＝∠FCE.

又∵∠DBE＝∠EFC＝120°，

∴△DBE≌△EFC，

∴DB＝EF，

∴AE＝BD.

方法二：在等边三角形ABC中，

∠ABC＝∠ACB＝60°，∠ABD＝120°.

∵∠ABC＝∠EDB＋∠BED，∠ACB＝∠ECB＋∠ACE，

ED＝EC，

∴∠EDB＝∠ECB，

∴∠BED＝∠ACE.

∵FE∥BC，

∴∠AEF＝∠AFE＝60°＝∠BAC，

∴△AEF是正三角形，∠EFC＝180°－∠ACB＝120°＝∠ABD.

∴△EFC≌△DBE，

∴DB＝EF，

而由△AEF是正三角形可得EF＝AE.

∴AE＝DB.

（3）3)1或3.

随堂检测

1、【解析】∵△ABC是等边三角形，∴∠ACB=60°，

∠ACD=120°.∵CG=CD，∴∠CDG=30°，

∠FDE=150°.∵DF=DE，∴∠E=15°.

答案：15

2、【解析】∵△ABC是等边三角形，E是BC的中点，

∴∠CAE=30°.

根据旋转的性质，知∠CAE=∠DAF=30°，

∴∠CAF=30°，∴∠EAF=60°.

答案：60°

3．

【解析】选C.连接MA，NA.∵AB的垂直

平分线交BC于点M，交AB于点E，AC的

垂直平分线交BC于点N，交AC于点F，

∴BM=AM，CN=AN，

∴∠MAB=∠B，∠CAN=∠C.∵∠BAC=120°，AB=AC，

∴∠B=∠C=30°，∴∠BAM+∠CAN=60°，∠AMN=∠ANM=60°，

∴△AMN是等边三角形，

∴AM=AN=MN，∴BM=MN=NC，∴MN=  BC=2cm.

4、【解析】∵MN是AB的垂直平分线，

∴AD=BD，∴∠A=∠ABD，

∵∠DBC=15°，

∴∠ABC=∠A+15°，

∵AB=AC，

∴∠C=∠ABC=∠A+15°，

∴∠A+∠A+15°+∠A+15°=180°，

解得∠A=50°.

答案：50°

5、【解析】(1)如图所示，DE就是要求作的AB边上的垂直平分线.

(2)∵DE是AB边上的垂直平分线，∠A=30°

∴AD=BD，

∴∠ABD=∠A=30°.

∵∠C=90°，

∴∠ABC=90°-∠A=90°-30°=60°.

∴∠CBD=∠ABC-∠ABD=60°-30°=30°.

∴∠ABD=∠CBD，

即BD平分∠CBA.