

江西省吉安市泰和县2022年九年级上学期期末数学试卷(附答案)
展开九年级上学期期末数学试卷
一、单选题
1.二次函数的顶点坐标是( )
A.(﹣2,7) B.(2,7)
C.(﹣2,﹣7) D.(2,﹣7)
2.从甲、乙、丙三名男生和A、B两名女生中随机选出一名学生参加问卷调查,则选出女生的可能性是( )
A. B. C. D.
3.某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为( )
A.80(1+x)2=100 B.100(1﹣x)2=80
C.80(1+2x)=100 D.80(1+x2)=100
4.关于反比例函数y=,下列说法中错误的是( )
A.它的图象分布在一、三象限
B.当x>﹣1时,y<﹣3
C.当x>0时,y的值随x的增大而减小
D.若点(a,b)在它的图象上,则(b,a)也在图象上
5.如图,△ABC中,BD、CE是两条中线,则S△ADE:S△DEF=( )
A.2:1 B.4:1 C.3:1 D.5:2
6.如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
A. B. C. D.
二、填空题
7.若,则的值是 .
8.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,它的影子QN=1.8m,MN=0.8m,木竿PQ的长度为 .
9.如图,在菱形ABCD中,点E是CD上一点,连接AE交对角线BD于点F,连接CF,若∠AED=50°,则∠BCF= 度.
10.一元二次方程x2﹣4x+2=0的两根为x1,x2,则x12﹣4x1+2x1x2的值为 .
11.如图,A、B两点分别在反比例函数(x>0)和(x>0)的图象上,且ABx轴,C为x轴上任意一点,则△ABC的面积为 .
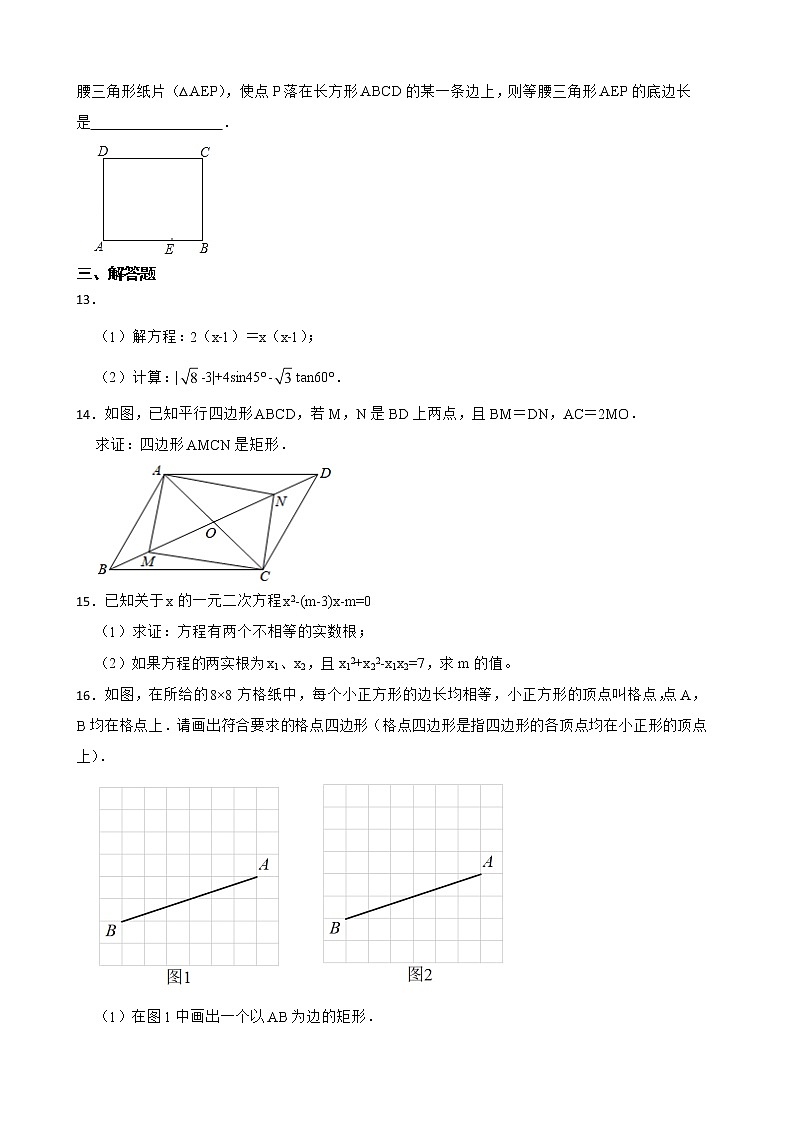
12.如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是 .
三、解答题
13.
(1)解方程:2(x﹣1)=x(x﹣1);
(2)计算:|﹣3|+4sin45°﹣tan60°.
14.如图,已知平行四边形ABCD,若M,N是BD上两点,且BM=DN,AC=2MO.
求证:四边形AMCN是矩形.
15.已知关于x的一元二次方程x2-(m-3)x-m=0
(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实根为x1、x2,且x12+x22-x1x2=7,求m的值。
16.如图,在所给的8×8方格纸中,每个小正方形的边长均相等,小正方形的顶点叫格点,点A,B均在格点上.请画出符合要求的格点四边形(格点四边形是指四边形的各顶点均在小正形的顶点上).
(1)在图1中画出一个以AB为边的矩形.
(2)在图2中画出一个以AB为对角线的正方形.
17.如图,在△ABC中,∠A=30°,∠B=45°,AC=,求AB的长.
18.由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达 处时,测得小岛 位于它的北偏东 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛 位于它的北偏东 方向.如果航母继续航行至小岛 的正南方向的 处,求还需航行的距离 的长.
(参考数据: , , , , , )
19.如图,在矩形ABCD中,对角线AC的垂直平分线分别与边AB和边CD的延长线交于点M,N,与边AD交于点E,垂足为点O.
(1)求证:△AOM≌△CON;
(2)若AB=4,AD=8,求AE的长.
20.为助力泰和县“四城同创”(全国文明城市、全国卫生县城、国家森林城市、省级生态园林城市)工作深入开展,某校组织志愿者进行宣传活动.班主任陈老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,陈老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠和小艳被同时抽中”的概率.
21.某商场经营某种品牌的玩具,购进的单价是30元,根据市场调查,在一段时间内,销售单价是40元时,销售量是600元,而销售单价每涨1元,就会少售出10件玩具.
(1)设该种品牌玩具的销售单价为x元,请你分别用x的代数式来表示销售量y件和销售该品牌玩具获利利润W元;
(2)在(1)的条件下,若商场获利了10000元销售利润,求该玩具销售单价x应定为多少元?
(3)在(1)的条件下,若玩具厂规定该品牌玩具销售单价不低于45元,且商场要完成不少于480件的销售任务,求商场销售该品牌玩具获利的最大利润是多少元?
22.如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.
(1)求证:△PFA∽△ABE;
(2)当点P在射线AD上运动时,设PA=x,是否存在实数x,使以P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,说明理由.
23.如图,抛物线的对称轴为直线x=﹣1,与x轴相交于A、B两点,与y轴相交于C,OA=OC,点A的坐标为(﹣3,0).
(1)求抛物线的表达式;
(2)若点P在抛物线上,且,求点P的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】A
7.【答案】
8.【答案】3.2m
9.【答案】50
10.【答案】2
11.【答案】1
12.【答案】5 或4 或5
13.【答案】(1)解:2(x﹣1)﹣x(x﹣1)=0,
(x﹣1)(2﹣x)=0,
x﹣1=0或2﹣x=0,
所以;
(2)解:原式=
=
=0.
14.【答案】证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵MO=NO,
∴MN=2MO,
∵AC=2MO,
∴MN=AC,
∴四边形AMCN是矩形.
15.【答案】(1)解:A=[-(m-1)]2-4×1×(-m)
=m2-2m+9
=(m-1)2+8
∵(m-1)2≥0
∴Δ=(m-1)2+8>0
∴此方程必有两个不等的数根
(2)解:x12+x22-x1x2=7
(x1+x2)2-3x1x2=7
即(m-3)2+3m=7
解得:m1=1,m2=2
∴m的值为1或2
16.【答案】(1)解:如图1中,矩形ABCD即为所求;
连接AC,
根据勾股定理可得:,,
∴AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∵,
∴,
∠B=90°,
∴四边形ABCD是矩形.
(2)解:如图2中,正方形AEBF即为所求.
根据勾股定理可得:,
∴四边形AEBF是菱形,
∵,
∴∠E=90°,
∴四边形AEBF是正方形.
17.【答案】过点C作CD⊥AB于D.
在Rt△ACD中,∵∠A=30°,AC=
∴CD=,
∴AD=AC×cosA=×=3
在Rt△BCD中,∠B=45°,则BD=CD=,
∴AB=AD+BD=3+
18.【答案】解:由题知: , , .
在 中, , , (海里).
在 中, , , (海里).
答:还需要航行的距离 的长为20.4海里.
19.【答案】(1)证明:∵四边形ABCD是矩形,
∴ABCD,
∴∠M=∠N,
∵AC的垂直平分线是MN,
∴AO=CO,
在△AOM和△CON中,
,
∴△AOM≌△CON(AAS);
(2)解:连接CE,设AE=x,则DE=8﹣x,
∵AC的垂直平分线是MN,
∴AE=CE=x,
∵四边形ABCD是矩形,AB=4,
∴DC=AB=4,∠ADC=90°,
由勾股定理得:,
∴,
解得:x=5,
即AE=5.
20.【答案】(1)不可能|随机|
(2)解:记小悦、小惠、小艳和小倩这四位女同学分别为A、B、C、D,列表如下:
| A | B | C | D |
A |
| (B,A) | (C,A) | (D,A) |
B | (A,B) |
| (C,B) | (D,B) |
C | (A,C) | (B,C) |
| (D,C) |
D | (A,D) | (B,D) | (C,D) |
|
由表可知,共有12种等可能结果,其中“小惠和小艳被同时抽中“的有2种结果,
所以“小惠和小艳被同时抽中“的概率为.
21.【答案】(1)解:依等量关系式“销量=原销量-因涨价而减少销量,总利润=单个利润×销量”可列式为:
y=600-10(x-40)=-10x+1000;
W=(x-30)(-10x+1000)=-10 +1300x-30000
(2)解:由题意可得: 10 +1300x 30000=10000,
解得:x=50或x=80,
∴该玩具销售单价x应定为50元或80元
(3)解:由题意可得: ,
解得:45≤x≤52,
W= 10 +1300x 30000= 10( +12250,
∵ 10<0,W随x的增大而减小,
又∵45≤x≤52,
∴当x=52时,W有最大值,最大值为10560元,
∴商场销售该品牌玩具获利的最大利润是10560元.
22.【答案】(1)证明:∵AD∥BC,
∴∠PAF=∠AEB.
∵∠PFA=∠ABE=90°,
∴△PFA∽△ABE.
(2)解:若△EFP∽△ABE,则∠PEF=∠EAB.
∴PE∥AB.
∴四边形ABEP为矩形.
∴PA=EB=2,即x=2.
若△PFE∽△ABE,则∠PEF=∠AEB.
∵∠PAF=∠AEB,
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点.
∵AE= ,
∴EF= AE= .
∵ ,即 ,
∴PE=5,即x=5.
∴满足条件的x的值为2或5.
23.【答案】(1)解:令x=0,则y=c,
∴OC=﹣c,
∵OA=OC,
∴3=﹣c,即c=﹣3.
∵对称轴是直线x=﹣1,点A的坐标为(﹣3,0),
根据题意得:,
解之:.
∴抛物线解析式.
(2)解:当x=0时,y=﹣3,
∴点C(0,﹣3),即OC=3,
∵A,B关于对称轴对称,
∴B(1,0),即OB=1,
∴,
设,
∴=×3×|x|,
∵=,
∴,
∴x=±4,
∴P(4,21),(﹣4,5).
(3)解:∵点A(﹣3,0),点C(0,﹣3),
∴直线AC解析式y=﹣x﹣3,
∴设点Q(m,﹣m﹣3)(﹣3≤m≤0),
则点,
∴,
∴当m=﹣时,QD的最大值为 .
江西省吉安市泰和县2022-2023学年九年级上学期期末数学试题(含答案): 这是一份江西省吉安市泰和县2022-2023学年九年级上学期期末数学试题(含答案),共11页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
江西省吉安市泰和县2021-2022学年九年级(上)期末数学试卷(含答案): 这是一份江西省吉安市泰和县2021-2022学年九年级(上)期末数学试卷(含答案),共25页。试卷主要包含了精心选一选,耐心填一填,细心做一做,沉着冷静,周密考虑,开动脑筋,再接再厉,充满信心,成功在望等内容,欢迎下载使用。
2021-2022学年江西省吉安市泰和县八年级(上)期末数学试卷(含解析): 这是一份2021-2022学年江西省吉安市泰和县八年级(上)期末数学试卷(含解析),共18页。












