

上海市文建中学2022-2023学年高一上学期期中考试数学试卷
展开上海市文建中学2022-2023学年高一上学期期中数学试卷
一、填空题。(本大题共有12题,满分54分)考生应在答题纸相应编号的空格内直接填写结果,每个空格填对前6题得4分、后6题得5分,否则一律得零分.
1.(4分)已知集合A={2,3},B={1,2,a},若A⊆B,则实数a= .
2.(4分)已知函数f(x)=x3﹣2x+1,则f'(2)= .
3.(4分)函数f(x)=的定义域为 .
4.(4分)已知复数z(1+i)=2,则z= .
5.(4分)已知α∈(0,π),且cosα=﹣,则tanα= .
6.(4分)已知等差数列{an}满足:a1+a3=6,a2+a4=10,则an= .
7.(5分)已知向量,,若向量∥,则实数m= .
8.(5分)已知y=(m﹣1)x2+(1﹣m)x+2的值恒小于3,则实数m的取值范围是 .
9.(5分)某驾驶员喝了m升酒后,血液中的酒精含量f(x)(毫克/毫升)随时间x(小时)变化的规律近似满足表达式《酒后驾车与醉酒驾车的标准及相应的处罚》规定:驾驶员血液中酒精含量不得超过0.02毫克/毫升.此驾驶员至少要过 小时后才能开车.(精确到1小时)
10.(5分)给定两个长度为1的平面向量,它们的夹角为120°,如图所示,点C在以O为圆心的圆弧AB上运动,若,其中x,y∈R,则x+y的取值范围是 .
11.(5分)已知函数,若关于x的方程[f(x)]2+mf(x)+2m+3=0有三个不相等的实数解,则实数m的取值范围为 .
12.(5分)设a∈R,对任意实数x,记f(x)=min{|x|﹣2,x2﹣ax+3a﹣5}.若f(x)至少有3个零点,则实数a的取值范围为 .
二、选择题。(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生应在答题卷的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.
13.(5分)设全集U={﹣2,﹣1,0,1,2},集合A={0,1,2},B={﹣1,2},则A∩(∁UB)=( )
A.{0,1} B.{0,1,2} C.{﹣1,1,2} D.{0,﹣1,1,2}
14.(5分)要得到函数y=2sin(2x+)的图象,只要将y=2sin2x的图象( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
15.(5分)设z1,z2为复数,则下列命题中一定成立的是( )
A.如果z1﹣z2>0,那么z1>z2
B.如果|z1|=|z2|,那么z1=±z2
C.如果,那么|z1|>|z2|
D.如果z12+z22=0,那么z1=z2=0
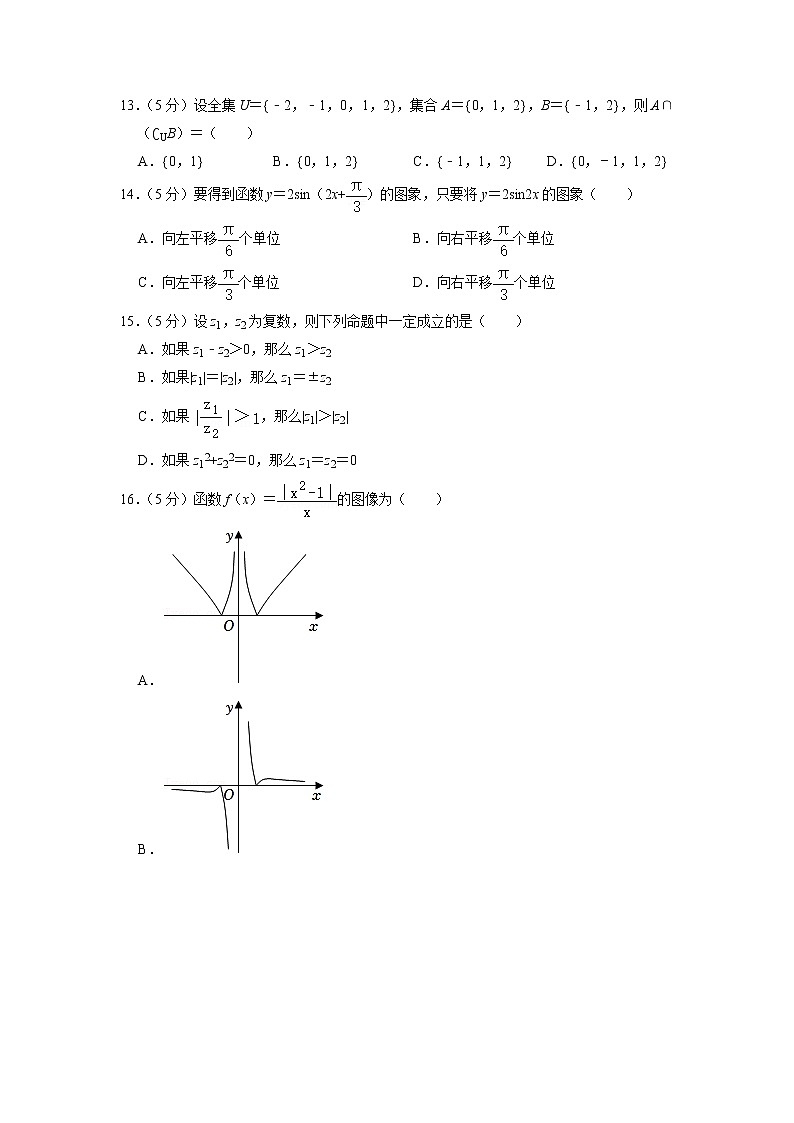
16.(5分)函数f(x)=的图像为( )
A.
B.
C.
D.
三、解答题。(本大题满分76分)本大题共有5题,解答下列各题必须在答题卷的相应编号规定区域内写出必要的步骤。
17.(15分)已知函数f(x)=x2﹣lnx,(x>0).点P(1,f(1))是函数f(x)图象上一点.
(1)求过点P作函数f(x)图像的切线方程;
(2)求函数y=f(x)的单调递减区间.
18.(15分)已知向量=(cosωx,sinωx),=(cosωx,cosωx)其中ω>0,记f(x)=•.
(1)若函数f(x)的最小正周期为π,求ω的值;
(2)在(1)的条件下,已知△ABC的内角A,B,C对应的边分别为a,b,c,若f()=,且a=4,b+c=5.求△ABC的面积.
19.(15分)新冠肺炎疫情造成医用防护服短缺,某地政府决定为防护服生产企业A公司扩大生产提供x(x∈[0,10])(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到(万件),其中k为工厂工人的复工率(k∈[0.5,1]).A公司生产t万件防护服还需投入成本(20+8x+50t)(万元).
(1)将A公司生产防护服的利润y(万元)表示为补贴x(万元)的函数;
(2)对任意的x∈[0,10](万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01).
20.(15分)已知函数f(x)=2x+2﹣x.
(1)求证:函数f(x)是偶函数;
(2)设a∈R,求关于x的函数y=22x+2﹣2x﹣2af(x)在x∈[0,+∞)时的最小值g(a)的表达式;
(3)若关于x的不等式mf(x)≤2﹣x+m﹣1在x∈(0,+∞)时恒成立,求实数m的取值范围.
21.(16分)定义:{an}是无穷数列,若存在正整数k使得对任意n∈N*,均有an+k>an(an+k<an)则称{an}是近似递增(减)数列,其中k叫近似递增(减)数列{an}的间隔数.
(1)若,{an}是不是近似递增数列,并说明理由;
(2)已知数列{an}的通项公式为,其前n项的和为Sn,若2是近似递增数列{Sn}的间隔数,求a的取值范围;
(3)已知,证明{an}是近似递减数列,并且4是它的最小间隔数.
上海市文建中学2022-2023学年高一上学期期中数学试卷
参考答案与试题解析
一、填空题。(本大题共有12题,满分54分)考生应在答题纸相应编号的空格内直接填写结果,每个空格填对前6题得4分、后6题得5分,否则一律得零分.
1.(4分)已知集合A={2,3},B={1,2,a},若A⊆B,则实数a= 3 .
【分析】利用子集的定义和性质直接求解.
【解答】解:∵集合A={2,3},B={1,2,a},A⊆B,
∴a=3.
故答案为:3.
【点评】本题考查实数值的求法,是基础题,解题时要认真审题,注意子集定义的合理运用.
2.(4分)已知函数f(x)=x3﹣2x+1,则f'(2)= 10 .
【分析】根据导数的公式即可得到结论.
【解答】解:∵f(x)=x3﹣2x+1,
∴f′(x)=3x2﹣2,
∴f'(2)=12﹣2=10,
故答案为:10.
【点评】本题主要考查导数的基本运算,比较基础.
3.(4分)函数f(x)=的定义域为 (﹣∞,0)∪[1,+∞) .
【分析】由根式内部的代数式大于等于0,然后求解分式不等式得答案.
【解答】解:要使原函数有意义,则,即,解得:x<0或x≥1.
∴函数f(x)=的定义域为(﹣∞,0)∪[1,+∞).
故答案为:(﹣∞,0)∪[1,+∞).
【点评】本题考查函数的定义域及其求法,考查了分式不等式的解法,是基础题.
4.(4分)已知复数z(1+i)=2,则z= 1﹣i .
【分析】把已知等式变形,再由复数代数形式的乘除运算化简得答案.
【解答】解:由(1+i)z=2,得,
故答案为:1﹣i.
【点评】本题考查复数代数形式的乘除运算,是基础的计算题.
5.(4分)已知α∈(0,π),且cosα=﹣,则tanα= .
【分析】根据同角三角函数关系式即可求解.
【解答】解:∵α∈(0,π),cosα=﹣<0,
α∈(,π),
∴sinα=.
则tanα==.
故答案为:﹣.
【点评】本题主要考查了同角三角函数关系式的应用,属于基本知识的考查.
6.(4分)已知等差数列{an}满足:a1+a3=6,a2+a4=10,则an= 2n﹣1 .
【分析】由题意结合等差数列的通项公式即可直接求解.
【解答】解:因为等差数列{an}满足a1+a3=6,a2+a4=10,
所以,解得a1=1,d=2,
则an=a1+(n﹣1)d=1+2×(n﹣1)=2n﹣1.
故答案为:2n﹣1.
【点评】本题主要考查了等差数列的通项公式的应用,属于基础题.
7.(5分)已知向量,,若向量∥,则实数m= .
【分析】根据平面向量的坐标运算与共线定理,列方程求出m的值.
【解答】解:向量,,
则﹣2=(1﹣2m,8),
又∥,
则﹣3(1﹣2m)﹣8m=0,
解得m=﹣.
故答案为:﹣.
【点评】本题考查了平面向量的共线定理与坐标运算问题,是基础题.
8.(5分)已知y=(m﹣1)x2+(1﹣m)x+2的值恒小于3,则实数m的取值范围是 (﹣3,1] .
【分析】y=(m﹣1)x2+(1﹣m)x+2<3恒成立,然后对m﹣1是否为0进行分类讨论,结合二次函数的性质可求.
【解答】解:由题意得y=(m﹣1)x2+(1﹣m)x+2<3恒成立,
当m=1时,2<3符合题意,
当m≠1时,(m﹣1)x2+(1﹣m)x﹣1<0恒成立,
解得﹣3<m<1,
综上,m的取值范围为(﹣3,1].
故答案为:(﹣3,1].
【点评】本题主要考查了二次不等式的恒成立问题,属于基础题.
9.(5分)某驾驶员喝了m升酒后,血液中的酒精含量f(x)(毫克/毫升)随时间x(小时)变化的规律近似满足表达式《酒后驾车与醉酒驾车的标准及相应的处罚》规定:驾驶员血液中酒精含量不得超过0.02毫克/毫升.此驾驶员至少要过 4 小时后才能开车.(精确到1小时)
【分析】欲求出此驾驶员至少要过多少小时后才能开车,只须求出经过多少时间驾驶员血液中酒精含量不超过0.02毫克/毫升,利用所给函数解析式,只须解使得f(x)≤0.02的x的最小值即可.
【解答】解:本题需分情况讨论:
(1)当0≤x≤1时,5x﹣2≤0.02,即x﹣2≤log50.02,x≤2+log50.02∉[0,1](舍).
(2)当x>1时,,即31﹣x≤0.1,1﹣x≤log30.1,x≥1﹣log30.1,即x≥4.
即此驾驶员至少要过 4小时后才能开车.
故答案为:4.
【点评】本题主要考查了分段函数的应用,不等式的解法,还考查了分类讨论的思想,属于基础题.
10.(5分)给定两个长度为1的平面向量,它们的夹角为120°,如图所示,点C在以O为圆心的圆弧AB上运动,若,其中x,y∈R,则x+y的取值范围是 [1,2] .
【分析】建立坐标系,得出点的坐标,进而可得向量的坐标,化已知问题为三角函数的最值求解,可得答案
【解答】解:由题意,以O为原点,OA为x轴的正向,建立如图所示的坐标系,
设C(cosθ,sinθ),0≤θ≤120°
可得A(1,0),B(﹣,),
由若=x(1,0)+y(﹣,)得,
x﹣y=cosθ,y=sinθ,
∴y=sinθ,
∴x+y=cosθ+sinθ=2sin(θ+30°),
∵0≤θ≤120°,
∴30°≤θ+30°≤150°,
∴1≤2sin(θ+30°)≤2
∴x+y的范围为[1,2],
故答案为:[1,2].
【点评】本题考查平面向量基本定理,建立坐标系是解决问题的关键,属中档题.
11.(5分)已知函数,若关于x的方程[f(x)]2+mf(x)+2m+3=0有三个不相等的实数解,则实数m的取值范围为 (﹣,﹣] .
【分析】分析f(x)的图象,可知关于f(x)的二次方程有2根,范围分别为(0,1)和(1,+∞),在按二次方程根的分布处理.
【解答】解:画出函数的图象,如图所示,
令y=f(x),则y2+my+2m+3=0有2个不相等的实数解,
其范围分别为(0,1)和[1,+∞),
则解得<m≤﹣
故答案为:(﹣,﹣].
【点评】考查含有绝对值函数的图象,复合函数根的个数问题的处理,属于拔高题;
12.(5分)设a∈R,对任意实数x,记f(x)=min{|x|﹣2,x2﹣ax+3a﹣5}.若f(x)至少有3个零点,则实数a的取值范围为 [10,+∞) .
【分析】设g(x)=x2﹣ax+3a﹣5,h(x)=|x|﹣2,分析可知函数g(x)至少有一个零点,可得出Δ≥0,求出a的取值范围,然后对实数a的取值范围进行分类讨论,根据题意可得出关于实数a的不等式,综合可求得实数a的取值范围.
【解答】解:设g(x)=x2﹣ax+3a﹣5,h(x)=|x|﹣2,由|x|﹣2=0可得x=±2.
要使得函数f(x)至少有3个零点,则函数g(x)至少有一个零点,
则Δ=a2﹣4(3a﹣5)≥0,
解得a≤2或a≥10.
①当a=2时,g(x)=x2﹣2x+1,作出函数g(x)、h(x)的图象如图所示:
此时函数f(x)只有两个零点,不满足题意;
②当a<2时,设函数g(x)的两个零点分别为x1、x2(x1<x2),
要使得函数f(x)至少有3个零点,则x2≤﹣2,
所以,,解得a∈∅;
③当a=10时,g(x)=x2﹣10x+25,作出函数g(x)、h(x)的图象如图所示:
由图可知,函数f(x)的零点个数为3,满足题意;
④当a>10时,设函数g(x)的两个零点分别为x3、x4(x3<x4),
要使得函数f(x)至少有3个零点,则x3≥2,
可得,解得a>4,此时a>10.
综上所述,实数a的取值范围是[10,+∞).
故答案为:[10,+∞).
【点评】本题考查了函数的零点、转化思想、分类讨论思想及数形结合思想,属于中难题.
二、选择题。(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生应在答题卷的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.
13.(5分)设全集U={﹣2,﹣1,0,1,2},集合A={0,1,2},B={﹣1,2},则A∩(∁UB)=( )
A.{0,1} B.{0,1,2} C.{﹣1,1,2} D.{0,﹣1,1,2}
【分析】直接利用集合的补集与交集的运算法则求解即可.
【解答】解:全集U={﹣2,﹣1,0,1,2},集合A={0,1,2},B={﹣1,2},
则A∩(∁UB)={0,1,2}∩{﹣2,0,1}={0,1}.
故选:A.
【点评】本题考查集合的交集,补集的运算法则的应用,是基础题.
14.(5分)要得到函数y=2sin(2x+)的图象,只要将y=2sin2x的图象( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
【分析】由题意利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
【解答】解:将y=2sin2x的图象向左平移个单位,可得函数y=2sin(2x+)的图象,
故选:A.
【点评】本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.
15.(5分)设z1,z2为复数,则下列命题中一定成立的是( )
A.如果z1﹣z2>0,那么z1>z2
B.如果|z1|=|z2|,那么z1=±z2
C.如果,那么|z1|>|z2|
D.如果z12+z22=0,那么z1=z2=0
【分析】通过反例判断A的正误;复数的模与复数的关系判断B、C的正误;反例判断D的正误即可.
【解答】解:对于A,反例z1=3+i,z2=1+i,满足,z1﹣z2>0,当时z1>z2不正确,所以A不正确;
对于B,反例z1=1+i,z2=1﹣i,满足|z1|=|z2|,但是z1=±z2不正确;
对于C,,那么|z1|>|z2|,正确;
对于D,反例z1=1+i,z2=1﹣i,满足z12+z22=0,不满足z1=z2=0,所以D不正确;
故选:C.
【点评】本题考查命题的真假的判断,复数的模以及复数的性质的判断,是基本知识的考查,基础题.
16.(5分)函数f(x)=的图像为( )
A.
B.
C.
D.
【分析】根据函数奇偶性和特殊点,即可判断.
【解答】解:函数f(x)=的定义域为(﹣∞,0)∪(0,+∞),
∴f(﹣x)==﹣f(x),
∴该函数为奇函数,故A错误;
x>0时,x→0,f(x)→+∞;x=1,f(x)=0;x→+∞,f(x)→+∞,
故BC错误,D正确.
故选:D.
【点评】本题考查函数图象,属于基础题.
三、解答题。(本大题满分76分)本大题共有5题,解答下列各题必须在答题卷的相应编号规定区域内写出必要的步骤。
17.(15分)已知函数f(x)=x2﹣lnx,(x>0).点P(1,f(1))是函数f(x)图象上一点.
(1)求过点P作函数f(x)图像的切线方程;
(2)求函数y=f(x)的单调递减区间.
【分析】(1)求出函数的导函数,即可求出切线的斜率,再由点斜式求出切线方程;
(2)解关于导函数的不等式f'(x)<0,即可求出函数的单调递减区间.
【解答】解:(1)因为f(x)=x2﹣lnx,所以f(1)=12﹣ln1=1,,
所以,即切点为(1,1),切线的斜率k=1,
所以切线方程为y﹣1=1(x﹣1),即y=x;
(2)f(x)=x2﹣lnx定义域为(0,+∞),且,
令f'(x)<0,解得,
所以f(x)的单调递减区间为.
【点评】本题考查导数的几何意义以及利用导数研究函数的单调性,考查运算求解能力,属于基础题.
18.(15分)已知向量=(cosωx,sinωx),=(cosωx,cosωx)其中ω>0,记f(x)=•.
(1)若函数f(x)的最小正周期为π,求ω的值;
(2)在(1)的条件下,已知△ABC的内角A,B,C对应的边分别为a,b,c,若f()=,且a=4,b+c=5.求△ABC的面积.
【分析】(1)进行数量积的坐标运算,并根据二倍角的正余弦公式及两角和的正弦公式得出,再根据f(x)的最小正周期为π即可求出ω=1;
(2)根据(1)可得出,然后根据即可求出A=,然后由余弦定理即可得出16=(b+c)2﹣3bc,从而求出bc=3,然后可求出△ABC的面积.
【解答】解:(1)==,
∴,
∵f(x)的最小正周期为π,且ω>0,
∴,解得ω=1;
(2)由(1)得,
∵,
∴,由0<A<π得,,
∴,解得,
由余弦定理知:a2=b2+c2﹣2bccosA,即16=b2+c2﹣bc=(b+c)2﹣3bc,且b+c=5,
∴16=25﹣3bc,∴bc=3,
∴.
【点评】本题考查了向量数量积的坐标运算,二倍角的正余弦公式,两角和的正弦公式,已知三角函数值求角,余弦定理,三角形的面积公式,考查了计算能力,属于基础题.
19.(15分)新冠肺炎疫情造成医用防护服短缺,某地政府决定为防护服生产企业A公司扩大生产提供x(x∈[0,10])(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到(万件),其中k为工厂工人的复工率(k∈[0.5,1]).A公司生产t万件防护服还需投入成本(20+8x+50t)(万元).
(1)将A公司生产防护服的利润y(万元)表示为补贴x(万元)的函数;
(2)对任意的x∈[0,10](万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01).
【分析】(1)利用已知条件列出函数的解析式,写出定义域即可.
(2)若对任意的x∈[0,10],公司都不产生亏损,得到在x∈[0,10]恒成立,利用换元法,结合函数的单调性求解函数的最值即可得到结果.
【解答】解:(1)y=x+80t﹣(20+8x+50t)=30t﹣20﹣7x,
=,x∈[0,10].
(2)若对任意的x∈[0,10],公司都不产生亏损,
则在x∈[0,10]恒成立,
即180k≥,记t=x+2,则t∈[2,12],
此时==7t+,
由于函数f(t)=7t+在t∈[2,12]单调递增,
所以当t∈[2,12]时,fmax(t)=f(12)=105,
∴k≥≈0.583即k取0.59,
即当工厂工人的复工率达到0.59时,对任意的x∈[0,10],公司都不产生亏损.
【点评】本题考查实际问题的处理方法,函数的单调性以及函数的解析式的求法,考查转化思想以及计算能力,是中档题.
20.(15分)已知函数f(x)=2x+2﹣x.
(1)求证:函数f(x)是偶函数;
(2)设a∈R,求关于x的函数y=22x+2﹣2x﹣2af(x)在x∈[0,+∞)时的最小值g(a)的表达式;
(3)若关于x的不等式mf(x)≤2﹣x+m﹣1在x∈(0,+∞)时恒成立,求实数m的取值范围.
【分析】(1)先说明定义域关于原点对称,再证明f(﹣x)=f(x)即可证明函数为偶函数;
(2)换元令t=f(x),将函数表示为关于t的二次函数,分类讨论a的取值,求出相应最小值;
(3)独立参数m,换元令t=1﹣2x,将问题转化为求函数的最小值,求得m的取值范围.
【解答】(1)证明:f(x)的定义域为R,关于原点对称,
又因为f(﹣x)=2﹣x+2x=f(x),所以f(x)为偶函数.
(2)解:令t=f(x)=2x+2﹣x,因为x∈[0,+∞),所以t∈[2,+∞),
则y=22x+2﹣2x﹣2af(x)可化为y=t2﹣2at﹣2,t∈[2,+∞),
若a≤2,函数在[2,+∞)上单调递增,当t=2时函数取最小值g(a)=﹣4a+2,
若a>2,函数在(2,a)上单调递减,在(a,+∞)上单调递增,
当t=a时函数取最小值g(a)=﹣a2﹣2,∴.
(3)解:由题,m(2x+2﹣x﹣1)≤2﹣x﹣1在(0,+∞)上恒成立,
当x∈(0,+∞)时,2x+2﹣x﹣1>0,
即在(0,+∞)上恒成立,
令t=1﹣2x,因为x∈(0,+∞),t∈(﹣∞,0),
即在t∈(﹣∞,0)上恒成立,
因为t∈(﹣∞,0),,当且仅当t=﹣1时等号成立,
所以.
【点评】使用换元法可以简化函数,不论是单调性问题,还是最值问题都可以更容易解决,换元要注意新未知数的取值范围.
21.(16分)定义:{an}是无穷数列,若存在正整数k使得对任意n∈N*,均有an+k>an(an+k<an)则称{an}是近似递增(减)数列,其中k叫近似递增(减)数列{an}的间隔数.
(1)若,{an}是不是近似递增数列,并说明理由;
(2)已知数列{an}的通项公式为,其前n项的和为Sn,若2是近似递增数列{Sn}的间隔数,求a的取值范围;
(3)已知,证明{an}是近似递减数列,并且4是它的最小间隔数.
【分析】(1)直接利用关系式的应用求出数列是近似递增数列.
(2)利用数列的和,进一步确定a的范围.
(3)利用由an+k<an得:,即k>2[sin(n+k)﹣sinn],进一步利用赋值法的应用求出结果.
【解答】解:(1)数列{an}是近似递增数列,
由于﹣[n+(﹣1)n]=3﹣2(﹣1)n>0,
或,
即an+3>an,或an+2>an.
所以:数列{an}是近似递增数列,
(2)由题意得:=,
或,
即恒成立.
令,则,
即a的取值范围是().
(3)由an+k<an得:,
即k>2[sin(n+k)﹣sinn]①,
由于n和k为正整数,所以sinn和sin(n+k)均取不到±1.
所以k=4时,上式恒成立,即数列{an}是近似递减数列,4是它的间隔数.
当k=3时,当n=5时,2[sin(5+3)﹣sin5]≈3.9>3,故不等式①成立.
当k=2时,当n=5时,2[sin(5+2)﹣sin5]≈3.23>32故不等式①不成立.
当k=1时,当n=5时,2[sin(5+1)﹣sin5]≈1.36>1,故不等式①不成立.
所以4是它的最小间隔数.
【点评】本题考查的知识要点:数列的通项公式和前n项和公式的应用,恒成立问题的应用,不等式的性质的应用,赋值法的应用,主要考查学生的运算能力和转换能力及思维能力,属于中档题型.
上海市虹口高级中学2023-2024学年高一上学期期中考试数学试卷: 这是一份上海市虹口高级中学2023-2024学年高一上学期期中考试数学试卷,共4页。
上海市进才中学2023-2024学年高一上学期期中考试数学试卷: 这是一份上海市进才中学2023-2024学年高一上学期期中考试数学试卷,共4页。
上海市南汇中学2023-2024学年高一上学期期中考试数学试卷: 这是一份上海市南汇中学2023-2024学年高一上学期期中考试数学试卷,文件包含第1课时初步认识比热容pptx、加热水和煤油mp4、比较水沙石的比热容mp4、比较金属的比热熔冰mp4、水和煤油的吸热能力对比mp4、水和煤油的吸热能力对比swf等6份课件配套教学资源,其中PPT共23页, 欢迎下载使用。












