专题09 概率与统计-2022年高考真题和模拟题数学分类汇编(解析版)

这是一份专题09 概率与统计-2022年高考真题和模拟题数学分类汇编(解析版)，共31页。

专题09 概率与统计

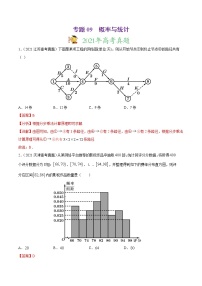
1．【2022年全国甲卷】某社区通过公益讲座以普及社区居民的垃圾分类知识．为了解讲座效果，随机抽取10位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷，这10位社区居民在讲座前和讲座后问卷答题的正确率如下图：

则（       ）
A．讲座前问卷答题的正确率的中位数小于70%
B．讲座后问卷答题的正确率的平均数大于85%
C．讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D．讲座后问卷答题的正确率的极差大于讲座前正确率的极差
【答案】B
【解析】
【分析】
由图表信息，结合中位数、平均数、标准差、极差的概念，逐项判断即可得解.
【详解】
讲座前中位数为70%+75%2>70%,所以A错；
讲座后问卷答题的正确率只有一个是80%,4个85%,剩下全部大于等于90%,所以讲座后问卷答题的正确率的平均数大于85%,所以B对；
讲座前问卷答题的正确率更加分散,所以讲座前问卷答题的正确率的标准差大于讲座后正确率的标准差,所以C错；
讲座后问卷答题的正确率的极差为100%−80%=20%，
讲座前问卷答题的正确率的极差为95%−60%=35%>20%,所以D错.
故选:B.
2．【2022年全国甲卷】从分别写有1，2，3，4，5，6的6张卡片中无放回随机抽取2张，则抽到的2张卡片上的数字之积是4的倍数的概率为（       ）
A．15 B．13 C．25 D．23
【答案】C
【解析】
【分析】
先列举出所有情况，再从中挑出数字之积是4的倍数的情况，由古典概型求概率即可.
【详解】
从6张卡片中无放回抽取2张，共有1,2,1,3,1,4,1,5,1,6,2,3,2,4,2,5,2,6,3,4,3,5,3,6,4,5,4,6,5,615种情况，
其中数字之积为4的倍数的有1,4,2,4,2,6,3,4,4,5,4,66种情况，故概率为615=25.
故选：C.
3．【2022年全国乙卷】分别统计了甲、乙两位同学16周的各周课外体育运动时长（单位：h），得如下茎叶图：

则下列结论中错误的是（       ）
A．甲同学周课外体育运动时长的样本中位数为7.4
B．乙同学周课外体育运动时长的样本平均数大于8
C．甲同学周课外体育运动时长大于8的概率的估计值大于0.4
D．乙同学周课外体育运动时长大于8的概率的估计值大于0.6
【答案】C
【解析】
【分析】
结合茎叶图、中位数、平均数、古典概型等知识确定正确答案.
【详解】
对于A选项，甲同学周课外体育运动时长的样本中位数为7.3+7.52=7.4，A选项结论正确.
对于B选项，乙同学课外体育运动时长的样本平均数为：
6.3+7.4+7.6+8.1+8.2+8.2+8.5+8.6+8.6+8.6+8.6+9.0+9.2+9.3+9.8+10.116=8.50625>8，
B选项结论正确.
对于C选项，甲同学周课外体育运动时长大于8的概率的估计值616=0.375<0.4，
C选项结论错误.
对于D选项，乙同学周课外体育运动时长大于8的概率的估计值1316=0.8125>0.6，
D选项结论正确.
故选：C
4．【2022年全国乙卷】某棋手与甲、乙、丙三位棋手各比赛一盘，各盘比赛结果相互独立．已知该棋手与甲、乙、丙比赛获胜的概率分别为p1,p2,p3，且p3>p2>p1>0．记该棋手连胜两盘的概率为p，则（       ）
A．p与该棋手和甲、乙、丙的比赛次序无关 B．该棋手在第二盘与甲比赛，p最大
C．该棋手在第二盘与乙比赛，p最大 D．该棋手在第二盘与丙比赛，p最大
【答案】D
【解析】
【分析】
该棋手连胜两盘，则第二盘为必胜盘.分别求得该棋手在第二盘与甲比赛且连胜两盘的概率p甲；该棋手在第二盘与乙比赛且连胜两盘的概率p乙；该棋手在第二盘与丙比赛且连胜两盘的概率p丙.并对三者进行比较即可解决
【详解】
该棋手连胜两盘，则第二盘为必胜盘，
记该棋手在第二盘与甲比赛，且连胜两盘的概率为p甲
则p甲=2(1−p2)p1p3+2p2p1(1−p3)=2p1(p2+p3)−4p1p2p3
记该棋手在第二盘与乙比赛，且连胜两盘的概率为p乙
则p乙=2(1−p1)p2p3+2p1p2(1−p3)=2p2(p1+p3)−4p1p2p3
记该棋手在第二盘与丙比赛，且连胜两盘的概率为p丙
则p丙=2(1−p1)p3p2+2p1p3(1−p2)=2p3(p1+p2)−4p1p2p3
则p甲−p乙=2p1(p2+p3)−4p1p2p3−2p2(p1+p3)−4p1p2p3=2p1−p2p3<0
p乙−p丙=2p2(p1+p3)−4p1p2p3−2p3(p1+p2)−4p1p2p3=2p2−p3p1<0
即p甲 则该棋手在第二盘与丙比赛，p最大.选项D判断正确；选项BC判断错误；
p与该棋手与甲、乙、丙的比赛次序有关.选项A判断错误.
故选：D
5．【2022年新高考1卷】从2至8的7个整数中随机取2个不同的数，则这2个数互质的概率为（       ）
A．16 B．13 C．12 D．23
【答案】D
【解析】
【分析】
由古典概型概率公式结合组合、列举法即可得解.
【详解】
从2至8的7个整数中随机取2个不同的数，共有C72=21种不同的取法，
若两数不互质，不同的取法有：(2,4),(2,6),(2,8),(3,6),(4,6),(4,8),(6,8)，共7种，
故所求概率P=21−721=23.
故选：D.
6．【2022年全国甲卷】从正方体的8个顶点中任选4个，则这4个点在同一个平面的概率为________．
【答案】635.
【解析】
【分析】
根据古典概型的概率公式即可求出．
【详解】
从正方体的8个顶点中任取4个，有n=C84=70个结果，这4个点在同一个平面的有m=6+6=12个，故所求概率P=mn=1270=635．
故答案为：635．
7．【2022年全国乙卷】从甲、乙等5名同学中随机选3名参加社区服务工作，则甲、乙都入选的概率为____________．
【答案】310##0.3
【解析】
【分析】
根据古典概型计算即可
【详解】
从5名同学中随机选3名的方法数为C53=10
甲、乙都入选的方法数为C31=3，所以甲、乙都入选的概率P=310
故答案为：310
8．【2022年新高考2卷】已知随机变量X服从正态分布N2,σ2，且P(22.5)=____________．
【答案】0.14##750．
【解析】
【分析】
根据正态分布曲线的性质即可解出．
【详解】
因为X∼N2,σ2，所以PX<2=PX>2=0.5，因此PX>2.5=PX>2−P2 故答案为：0.14．
9．【2022年浙江】现有7张卡片，分别写上数字1，2，2，3，4，5，6．从这7张卡片中随机抽取3张，记所抽取卡片上数字的最小值为ξ，则P(ξ=2)=__________，E(ξ)=_________．
【答案】     1635，     127##157
【解析】
【分析】
利用古典概型概率公式求P(ξ=2)，由条件求ξ分布列，再由期望公式求其期望.
【详解】
从写有数字1,2,2,3,4,5,6的7张卡片中任取3张共有C73种取法，其中所抽取的卡片上的数字的最小值为2的取法有C41+C21C42种，所以P(ξ=2)=C41+C21C42C73=1635，
由已知可得ξ的取值有1，2，3，4，
P(ξ=1)=C62C73=1535，P(ξ=2)=1635，
，P(ξ=3)=C32C73=335，P(ξ=4)=1C73=135
       所以E(ξ)=1×1535+2×1635+3×335+4×135=127,
故答案为：1635，127.
10．【2022年全国甲卷】甲、乙两城之间的长途客车均由A和B两家公司运营，为了解这两家公司长途客车的运行情况，随机调查了甲、乙两城之间的500个班次，得到下面列联表：

准点班次数
未准点班次数
A
240
20
B
210
30
(1)根据上表，分别估计这两家公司甲、乙两城之间的长途客车准点的概率；
(2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关？
附：K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)，
PK2⩾k
0.100
0.050
0.010
k
2.706
3.841
6.635
【答案】(1)A，B两家公司长途客车准点的概率分别为1213，78
(2)有
【解析】
【分析】
（1）根据表格中数据以及古典概型的概率公式可求得结果；
（2）根据表格中数据及公式计算K2，再利用临界值表比较即可得结论.
(1)根据表中数据，A共有班次260次，准点班次有240次，
设A家公司长途客车准点事件为M，
则P(M)=240260=1213；
B共有班次240次，准点班次有210次，
设B家公司长途客车准点事件为N，
则P(N)=210240=78.
A家公司长途客车准点的概率为1213；
B家公司长途客车准点的概率为78.
(2)列联表

准点班次数
未准点班次数
合计
A
240
20
260
B
210
30
240
合计
450
50
500
K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)=500×(240×30−210×20)2260×240×450×50≈3.205>2.706，
根据临界值表可知，有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关.
11．【2022年全国甲卷】甲、乙两个学校进行体育比赛，比赛共设三个项目，每个项目胜方得10分，负方得0分，没有平局．三个项目比赛结束后，总得分高的学校获得冠军．已知甲学校在三个项目中获胜的概率分别为0.5，0.4，0.8，各项目的比赛结果相互独立．
(1)求甲学校获得冠军的概率；
(2)用X表示乙学校的总得分，求X的分布列与期望．
【答案】(1)0.6；
(2)分布列见解析，EX=13.
【解析】
【分析】
（1）设甲在三个项目中获胜的事件依次记为A,B,C，再根据甲获得冠军则至少获胜两个项目，利用互斥事件的概率加法公式以及相互独立事件的乘法公式即可求出；
（2）依题可知，X的可能取值为0,10,20,30，再分别计算出对应的概率，列出分布列，即可求出期望．
(1)
设甲在三个项目中获胜的事件依次记为A,B,C，所以甲学校获得冠军的概率为
P=PABC+PABC+PABC+PABC
=0.5×0.4×0.8+0.5×0.4×0.8+0.5×0.6×0.8+0.5×0.4×0.2
=0.16+0.16+0.24+0.04=0.6．
(2)
依题可知，X的可能取值为0,10,20,30，所以，
PX=0=0.5×0.4×0.8=0.16,
PX=10=0.5×0.4×0.8+0.5×0.6×0.8+0.5×0.4×0.2=0.44，
PX=20=0.5×0.6×0.8+0.5×0.4×0.2+0.5×0.6×0.2=0.34，
PX=30=0.5×0.6×0.2=0.06.
即X的分布列为
X
0
10
20
30
P
0.16
0.44
0.34
0.06
期望EX=0×0.16+10×0.44+20×0.34+30×0.06=13.
12．【2022年全国乙卷】某地经过多年的环境治理，已将荒山改造成了绿水青山．为估计一林区某种树木的总材积量，随机选取了10棵这种树木，测量每棵树的根部横截面积（单位：m2）和材积量（单位：m3），得到如下数据：
样本号ｉ
1
2
3
4
5
6
7
8
9
10
总和
根部横截面积xi
0.04
0.06
0.04
0.08
0.08
0.05
0.05
0.07
0.07
0.06
0.6
材积量yi
0.25
0.40
0.22
0.54
0.51
0.34
0.36
0.46
0.42
0.40
3.9

并计算得i=110xi2=0.038,i=110yi2=1.6158,i=110xiyi=0.2474．
(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量；
(2)求该林区这种树木的根部横截面积与材积量的样本相关系数（精确到0.01）；
(3)现测量了该林区所有这种树木的根部横截面积，并得到所有这种树木的根部横截面积总和为186m2．已知树木的材积量与其根部横截面积近似成正比．利用以上数据给出该林区这种树木的总材积量的估计值．
附：相关系数r=i=1n(xi−x)(yi−y)i=1n(xi−x)2i=1n(yi−y)2,1.896≈1.377．
【答案】(1)0.06m2；0.39m3
(2)0.97
(3)1209m3
【解析】
【分析】
（1）计算出样本的一棵根部横截面积的平均值及一棵材积量平均值，即可估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量；
（2）代入题给相关系数公式去计算即可求得样本的相关系数值；
（3）依据树木的材积量与其根部横截面积近似成正比，列方程即可求得该林区这种树木的总材积量的估计值．
(1)
样本中10棵这种树木的根部横截面积的平均值x=0.610=0.06
样本中10棵这种树木的材积量的平均值y=3.910=0.39
据此可估计该林区这种树木平均一棵的根部横截面积为0.06m2，
平均一棵的材积量为0.39m3
(2)
r=i=110(xi−x)(yi−y)i=110(xi−x)2i=110(yi−y)2=i=110xiyi−10xyi=110xi2−10x2i=110yi2−10y2
=0.2474−10×0.06×0.39(0.038−10×0.062)(1.6158−10×0.392)=0.01340.0001896≈0.01340.01377≈0.97
则r≈0.97
(3)
设该林区这种树木的总材积量的估计值为Ym3，
又已知树木的材积量与其根部横截面积近似成正比，
可得0.060.39=186Y，解之得Y=1209m3．
则该林区这种树木的总材积量估计为1209m3
13．【2022年新高考1卷】一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯（卫生习惯分为良好和不够良好两类）的关系，在已患该疾病的病例中随机调查了100例（称为病例组），同时在未患该疾病的人群中随机调查了100人（称为对照组），得到如下数据：

不够良好
良好
病例组
40
60
对照组
10
90
(1)能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异？
(2)从该地的人群中任选一人，A表示事件“选到的人卫生习惯不够良好”，B表示事件“选到的人患有该疾病”．P(B|A)P(B|A)与P(B|A)P(B|A)的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标，记该指标为R．
（ⅰ）证明：R=P(A|B)P(A|B)⋅P(A|B)P(A|B)；
（ⅱ）利用该调查数据，给出P(A|B),P(A|B)的估计值，并利用（ⅰ）的结果给出R的估计值．
附K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)，
PK2≥k
0.050
0.010
0.001
k
3.841
6.635
10.828
【答案】(1)答案见解析
(2)（i）证明见解析；(ii)R=6；
【解析】
【分析】
(1)由所给数据结合公式求出K2的值，将其与临界值比较大小，由此确定是否有99%的把握认为患该疾病群体与未黄该疾病群体的卫生习惯有差异；(2)(i) 根据定义结合条件概率公式即可完成证明；(ii)根据（i）结合已知数据求R.
(1)
由已知K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)=200(40×90−60×10)250×150×100×100=24，
又P(K2≥6.635)=0.01，24>6.635，
所以有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异.
(2)
(i)因为R=P(B|A)P(B|A)⋅P(B|A)P(B|A)=P(AB)P(A)⋅P(A)P(AB)⋅P(AB)P(A)⋅P(A)P(AB)，
所以R=P(AB)P(B)⋅P(B)P(AB)⋅P(AB)P(B)⋅P(B)P(AB)
所以R=P(A|B)P(A|B)⋅P(A|B)P(A|B)，
(ii)
由已知P(A|B)=40100，P(A|B)=10100，
又P(A|B)=60100，P(A|B)=90100，
所以R=P(A|B)P(A|B)⋅P(A|B)P(A|B)=6
14．【2022年新高考2卷】在某地区进行流行病学调查，随机调查了100位某种疾病患者的年龄，得到如下的样本数据的频率分布直方图：

(1)估计该地区这种疾病患者的平均年龄（同一组中的数据用该组区间的中点值为代表）；
(2)估计该地区一位这种疾病患者的年龄位于区间[20,70)的概率；
(3)已知该地区这种疾病的患病率为0.1%，该地区年龄位于区间[40,50)的人口占该地区总人口的16%.从该地区中任选一人，若此人的年龄位于区间[40,50)，求此人患这种疾病的概率．（以样本数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率，精确到0.0001）.
【答案】(1)44.65岁；
(2)0.89；
(3)0.0014．
【解析】
【分析】
（1）根据平均值等于各矩形的面积乘以对应区间的中点值的和即可求出；
（2）设A={一人患这种疾病的年龄在区间[20,70)}，根据对立事件的概率公式P(A)=1−P(A)即可解出；
（3）根据条件概率公式即可求出．
(1)
平均年龄x=(5×0.001+15×0.002+25×0.012+35×0.017+45×0.023
       +55×0.020+65×0.012+75×0.006+85×0.002)×10=44.65（岁）．
(2)
设A={一人患这种疾病的年龄在区间[20,70)}，所以
P(A)=1−P(A)=1−(0.001+0.002+0.006+0.002)×10=1−0.11=0.89．
(3)
设B={任选一人年龄位于区间[40,50)，C={任选一人患这种疾病}，
则由条件概率公式可得
P(C|B)=P(BC)P(B)=0.1%×0.023×1016%=0.001×0.230.16=0.0014375≈0.0014．
15．【2022年北京】在校运动会上，只有甲、乙、丙三名同学参加铅球比赛，比赛成绩达到9．50m以上（含9．50m）的同学将获得优秀奖．为预测获得优秀奖的人数及冠军得主，收集了甲、乙、丙以往的比赛成绩，并整理得到如下数据（单位：m）：
甲：9.80，9.70，9.55，9.54，9.48，9.42，9.40，935，9.30，9.25；
乙：9.78，9.56，9.51，9.36，9.32，9.23；
丙：9.85，9.65，9.20，9.16．
假设用频率估计概率，且甲、乙、丙的比赛成绩相互独立．
(1)估计甲在校运动会铅球比赛中获得优秀奖的概率；
(2)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数，估计X的数学期望E（X）；
(3)在校运动会铅球比赛中，甲、乙、丙谁获得冠军的概率估计值最大？（结论不要求证明）
【答案】(1)0.4
(2)75
(3)丙
【解析】
【分析】
(1)       由频率估计概率即可
(2)       求解得X的分布列，即可计算出X的数学期望.
(3)       计算出各自获得最高成绩的概率，再根据其各自的最高成绩可判断丙夺冠的概率估计值最大.
(1)
由频率估计概率可得
甲获得优秀的概率为0.4，乙获得优秀的概率为0.5，丙获得优秀的概率为0.5，
故答案为0.4
(2)
设甲获得优秀为事件A1,乙获得优秀为事件A2，丙获得优秀为事件A3
P(X=0)=P(A1A2A3)=0.6×0.5×0.5=320，
P(X=1)=P(A1A2A3)+P(A1A2A3)+P(A1A2A3)
=0.4×0.5×0.5+0.6×0.5×0.5+0.6×0.5×0.5=820，
P(X=2)=P(A1A2A3)+P(A1A2A3)+P(A1A2A3)
=0.4×0.5×0.5+0.4×0.5×0.5+0.6×0.5×0.5=720，
P(X=3)=P(A1A2A3)=0.4×0.5×0.5=220.
∴X的分布列为
X
0
1
2
3
P
320
820
720
220
∴E(X)=0×320+1×820+2×720+3×220=75
(3)
丙夺冠概率估计值最大.
因为铅球比赛无论比赛几次就取最高成绩.比赛一次，丙获得9.85的概率为14，甲获得9.80的概率为110，乙获得9.78的概率为16.并且丙的最高成绩是所有成绩中最高的，比赛次数越多，对丙越有利.

1．（2022·河南省杞县高中模拟预测（理））某市有11名选手参加了田径男子100米赛的选拔比赛，前5名可以参加省举办的田径赛，如果各个选手的选拔赛成绩均不相同，选手小强已经知道了自己的成绩，为了判断自己能否参加省举办的田径赛，他还需要知道这11名选手成绩的（       ）
A．平均数 B．中位数 C．众数 D．方差
【答案】B
【解析】
【分析】
中位数恰好是第6名，比中位数成绩高即可确认自己能否进入省田径赛．
【详解】
因为11名选手成绩的中位数恰好是第6名，知道了第6名的成绩，
小强就可以判断自己是否能参加省举办的田径赛了，其余数字特征不能反映名次．
故选：B．
2．（2022·黑龙江·大庆实验中学模拟预测（理））2021年5月30日清晨5时01分，天舟二号货运飞船在成功发射约8小时后，与中国空间站天和核心舱完成自主快速交接．如果下次执行空间站的任务由3名航天员承担，需要在3名女性航天员和3名男性航天员中选择，则选出的3名航天员中既有男性航天员又有女性航天员的概率为（       ）
A． B． C． D．
【答案】B
【解析】
【分析】
利用对立事件和古典概型的概率公式求解即可.
【详解】
设“选出的3名航天员中既有男性航天员又有女性航天员”为事件M，则.
故选：B.
3．（2022·全国·模拟预测（文））如图是一组实验数据的散点图，拟合方程，令，则关于的回归直线过点，，则当时，的取值范围是（       ）

A． B． C． D．
【答案】D
【解析】
【分析】
先令可得，由关于的回归直线过点，可得从而求得，再由的范围求得的范围，进而求得的范围.
【详解】
根据题意可得，
由关于的回归直线过点，可得：
，所以，
所以，
由可得，
所以，
所以，所以，
故选：D
4．（2022·辽宁实验中学模拟预测）某国计划采购疫苗，现在成熟的疫苗中，三种来自中国，一种来自美国，一种来自英国，一种由美国和德国共同研发，从这6种疫苗中随机采购三种，若采购每种疫苗都是等可能的，则买到中国疫苗的概率为（       ）
A． B． C． D．
【答案】D
【解析】
【分析】
由对立事件的概率公式计算．
【详解】
没有买到中国疫苗的概率为，
所以买到中国疫苗的概率为．
故选：D．
5．（2022·四川省泸县第二中学模拟预测（理））食物链亦称“营养链”，是指生态系统中各种生物为维持其本身的生命活动，必须以其他生物为食物的这种由食物联结起来的链锁关系．如图为某个生态环境中的食物链，若从鹰、麻雀、兔、田鼠以及蝗虫中任意选取两种，则这两种生物不能构成摄食关系的概率（       ）

A． B． C． D．
【答案】A
【解析】
【分析】
用列举法写出构成的摄食关系，计数后可求得概率．
【详解】
从鹰、麻雀、兔、田鼠以及蝗虫中任意选取两种，共有10种选法：鹰麻雀，鹰兔，鹰田鼠，鹰蝗虫，麻雀兔，麻雀田鼠，麻雀蝗虫，兔田鼠，兔蝗虫，田鼠蝗虫．
其中田鼠鹰，兔鹰，麻雀鹰，蝗虫麻雀共四种可构成摄食关系，不能构成摄食关系的有6种，
所以概率为．
故选：A．
6．（2022·山东潍坊·模拟预测）Poisson分布是统计学里常见的离散型概率分布，由法国数学家西莫恩·德尼·泊松首次提出，Poisson分布的概率分布列为，其中为自然对数的底数，是Poisson分布的均值．当二项分布的n很大而p很小时，Poisson分布可作为二项分布的近似．假设每个大肠杆菌基因组含有10000个核苷酸对，采用紫外线照射大肠杆菌时，每个核苷酸对产生嘧啶二体的概率均为0.0003，已知该菌株基因组有一个嘧啶二体就致死，则致死率是（       ）
A． B． C． D．
【答案】A
【解析】
【分析】
结合题意，，此时Poisson分布满足二项分布的近似条件，再计算二项分布的均值为Poisson分布的均值，再代入公式先求不致死的概率，再用对立事件的概率和为1计算即可
【详解】
由题， ，，此时Poisson分布满足二项分布的近似的条件，此时，故不致死的概率为，故致死的概率为
故选：A
7．（2022·河南安阳·模拟预测（理））某房产销售公司有800名销售人员，为了了解销售人员上一个季度的房屋销量，公司随机选取了部分销售人员对其房屋销量进行了统计，得到上一季度销售人员的房屋销量，则全公司上一季度至少完成22套房屋销售的人员大概有（       ）
附：若随机变量X服从正态分布，则，，．
A．254人 B．127人 C．18人 D．36人
【答案】B
【解析】
【分析】
根据正态分布的性质求出，从而估计出人数；
【详解】
解：因为，所以，，所以
所以全公司上一季度至少完成22套房屋销售的人员大概有（人）；
故选：B
8．（2022·河南·模拟预测）某公司生产的一种产品按照质量由高到低分为A，B，C，D四级，为了增加产量、提高质量，该公司改进了一次生产工艺，使得生产总量增加了一倍．为了解新生产工艺的效果，对改进生产工艺前、后的四级产品的占比情况进行了统计，绘制了如下扇形图：

根据以上信息：下列推断合理的是（       ）
A．改进生产工艺后，A级产品的数量没有变化
B．改进生产工艺后，D级产品的数量减少
C．改进生产工艺后，C级产品的数量减少
D．改进生产工艺后，B级产品的数量增加了不到一倍
【答案】C
【解析】
【分析】
由题可得改进生产工艺前后四个等级的生产量，逐项分析即得.
【详解】
设原生产总量为1，则改进生产工艺后生产总量为2，
所以原A，B，C，D等级的生产量为0.3，0.37，0.28，0.05，
改进生产工艺后四个等级的生产量为0.6，1.2，0.12，0.08，
故改进生产工艺后，A级产品的数量增加，故A错误；
改进生产工艺后，D级产品的数量增加，故B错误；
改进生产工艺后，C级产品的数量减少，故C正确；
改进生产工艺后，B级产品的数量增加超过2倍，故D错误.
故选：C.
9．（2022·河南安阳·模拟预测（文））为推动就业与培养有机联动、人才供需有效对接，促进高校毕业生更加充分更高质量就业，教育部今年首次实施供需对接就业育人项目．现安排甲、乙两所高校与3家用人单位开展项目对接，若每所高校至少对接两家用人单位，则两所高校的选择涉及到全部3家用人单位的概率为（       ）
A． B． C． D．
【答案】D
【解析】
【分析】
由古典概型与对立事件的概率公式求解即可
【详解】
因为每所高校至少对接两家用人单位，
所以每所高校共有种选择，
所以甲、乙两所高校共有种选择，
其中甲、乙两所高校的选择涉及两家用人单位的情况有种，
所以甲、乙两所高校的选择涉及到全部3家用人单位的概率为，
故选：D
10．（2022·江苏·南京师大附中模拟预测）某同学在课外阅读时了解到概率统计中的马尔可夫不等式，该不等式描述的是对非负的随机变量和任意的正数，都有，其中是关于数学期望和的表达式.由于记忆模糊，该同学只能确定的具体形式是下列四个选项中的某一种.请你根据自己的理解，确定该形式为（       ）
A． B． C． D．
【答案】D
【解析】
【分析】
根据期望的计算公式,以及即可求解.
【详解】
设非负随机变量的所有可能取值按从小到大依次为,对应的概率分别为设满足的有,,,因为,所以
故选：D
11．（2022·吉林·三模（理））为了切实维护居民合法权益，提高居民识骗防骗能力，守好居民的“钱袋子”，某社区开展“全民反诈在行动——反诈骗知识竞赛”活动，现从参加该活动的居民中随机抽取了100名，统计出他们竞赛成绩分布如下：
成绩（分）






人数
2
4
22
40
28
4
(1)求抽取的100名居民竞赛成绩的平均分和方差（同一组中数据用该组区间的中点值为代表）；
(2)以频率估计概率，发现该社区参赛居民竞赛成绩X近似地服从正态分布，其中近似为样本成绩平均分，近似为样本成缋方差，若，参赛居民可获得“参赛纪念证书”；若，参赛居民可获得“反诈先锋证书”，
①若该社区有3000名居民参加本次竞赛活动，试估计获得“参赛纪念证书”的居民人数（结果保留整数）；
②试判断竞赛成绩为96分的居民能否获得“反诈先锋证书”．
附：若，则，，．
【答案】(1)，
(2)①2456 ；②能
【解析】
【分析】
（1）利用公式直接求出均值、方差即可；
（2）①结合给的概率和正态分布的性质，确定获得“参赛纪念证书”，进而计算可得人数；
②利用正态分布的知识求出，即，进而可得结果.
(1)
100名居民本次竞赛成绩平均分
，
100名居民本次竞赛成绩方差

，
(2)
①由于近似为样本成绩平均分，近似为样本成绩方差，
所以，，
可知，，
由于竞赛成绩X近似地服从正态分布，
因此竞赛居民可获得“参赛纪念证书”的概率




估计获得“参赛纪念证书”的居民人数为2456；
②当时，即时，参赛居民可获得“反诈先锋证书”，
所以竞赛成绩为96分的居民能获得“反诈先峰证书”．
12．（2022·贵州·贵阳一中模拟预测（文））“十四五”规划纲要提出，全面推动长江经济带发展，协同推动生态环境保护和经济发展长江水资源约占全国总量的36%，长江流域河湖､水库､湿地面积约占全国的20%，珍稀濒危植物占全国的39.7%，淡水鱼类占全国的33%.长江经济带在我国生态文明建设中占据重要位置.长江流域某地区经过治理，生态系统得到很大改善，水生动物数量有所增加.为调查该地区某种水生动物的数量，将其分成面积相近的100个水域，从这些水域中用简单随机抽样的方法抽取20个作为样区，调查得到样本数据其中和分别表示第i个样区的水草覆盖面积（单位：公顷）和这种水生动物的数量，并计算得，
(1)求该地区这种水生动物数量的估计值（这种水生动物数量的估计值等于样区这种水生动物数量的平均数乘以地块数）；
(2)求样本的相关系数（精确到0.01）；
(3)根据现有统计资料，各地块间水草覆盖面积差异很大.为提高样本的代表性以获得该地区这种水生动物数量更准确的估计，请给出一种你认为更合理的抽样方法，并说明理由.
附：相关系数
【答案】(1)
(2)
(3)采用分层抽样的方法，理由见解析
【解析】
【分析】
（1）根据该地区这种水生动物数量的估计值的计算方法求解即可；
（2）根据相关系数的公式求解即可；
（3）根据（2）中的结论各样区的这种水生动物的数量与水草覆盖面积有很强的正相关性考虑即可
(1)
样区水生动物平均数为，
地块数为100，该地区这种水生动物的估计值为.
(2)
样本的相关系数为

(3)
由（2）知各样区的这种水生动物的数量与水草覆盖面积有很强的正相关性，由于各地块间水草覆盖面积差异很大，从而各地块间这种野生动物的数量差异很大，所以采用分层抽样的方法较好地保持了样本结构与总体结构得以执行，提高了样本的代表性，从而可以获得该地区这种水生动物数量更准确的估计.
13．（2022·河南开封·模拟预测（理））大豆是我国重要的农作物，种植历史悠久．某种子实验基地培育出某大豆新品种，为检验其最佳播种日期，在A，B两块试验田上进行实验（两地块的土质等情况一致）.6月25日在A试验田播种该品种大豆，7月10日在B试验田播种该品种大豆．收获大豆时，从中各随机抽取20份（每份1千粒），并测量出每份的质量（单位：克），按照，，进行分组，得到如下表格：




A试验田/份
3
6
11
B试验田/份
6
10
4

把千粒质量不低于200克的大豆视为籽粒饱满，否则视为籽粒不饱满．
(1)判断是否有97.5%的把握认为大豆籽粒饱满与播种日期有关？
(2)从A，B两块实验田中各抽取一份大豆，求抽取的大豆中至少有一份籽粒饱满的概率；
(3)用样本估计总体，从A试验田随机抽取100份（每份千粒）大豆，记籽粒饱满的份数为X，求X的数学期望和方差．
参考公式：，其中．

0.15
0.10
0.05
0.025
0.010
0.001

2.072
2.706
3.841
5.024
6.635
10.828
【答案】(1)有
(2)
(3)，
【解析】
【分析】
（1）根据完成列联表，然后根据公式计算，再与临界值表比较可得结论，
（2）A，B两块实验田中各抽取一份大豆中，籽粒饱满的概率分别为两份大豆都籽粒不饱满的概率为，再结合对立事件概率和为1求解即可；
（3）根据已知条件，结合二项分布的期望与方差公式，即可求解.
(1)
列联表为

6月25日播种
7月10日播种
合计
饱满
11
4
15
不饱满
9
16
25
合计
20
20
40
，
所以有97.5%的把握认为大豆籽粒饱满与播种日期有关．
(2)
A，B两块实验田中各抽取一份大豆，
抽取的大豆中有一份籽粒饱满的概率分别为，，
两份大豆籽粒都不饱满的概率为
故抽取的大豆中至少有一份籽粒饱满的概率为
.
(3)
从A试验田的样本中随机抽取1份小麦，抽到饱满的概率为，
则，故，
.
14．（2022·吉林吉林·模拟预测（文））为了切实维护居民合法权益，提高居民识骗防骗能力，守好居民的“钱袋子”，某社区开展“全民反诈在行动——反诈骗知识竞赛”活动，现从参加该活动的居民中随机抽取了100名，统计出他们竞赛成绩分布如下：
成绩X
人数

2

a

22

b

28

a

(1)求a，b的值，并补全频率分布直方图；
(2)估计该社区居民竞赛成绩的平均数和方差（同一组中的数据用该组区间的中点值作代表）；
(3)以频率估计概率，若，社区获得“反诈先进社区”称号，若，社区获得“反诈先锋社区”称号，试判断该社区可获得哪种称号（s为竞赛成绩标准差）？
【答案】(1)；，图见解析
(2)75，100
(3)该社区可获得“反诈先进社区”称号
【解析】
【分析】
（1）根据频率分布直方图与频率分布表求出、的值，从而补全频率分布直方图；
（2）根据频率分布直方图中平均数与方差公式计算可得；
（3）根据频率分布直方图求出，即可判断；
(1)
解：由题可知：，，
所以100名居民竞赛成绩在组内频率/组距为，
补全频率分布直方图如下：

(2)
解：估计该社区居民竞赛成绩的平均数
，
估计该社区居民竞赛成绩的方差


(3)
解：由（1）可得，
所以
∵
所以该社区可获得“反诈先进社区”称号．
15．（2022·辽宁·大连二十四中模拟预测）某汽车公司最近研发了一款新能源汽车，并在出厂前对100辆汽车进行了单次最大续航里程的测试.现对测试数据进行分析，得到如图所示的频率分布直方图：

(1)估计这100辆汽车的单次最大续航里程的平均值（同一组中的数据用该组区间的中点值代表）；
(2)经计算第（1）问中样本标准差的近似值为50，根据大量的测试数据，可以认为这款汽车的单次最大续航里程近似地服从正态分布（用样本平均数和标准差分别作为的近似值），现任取一辆汽车，求它的单次最大续航里程的概率；
（参考数据：若随机变量，则，
(3)某汽车销售公司为推广此款新能源汽车，现面向意向客户推出“玩游戏，送大奖”活动，客户可根据抛掷硬币的结果，操控微型遥控车在方格图上（方格图上依次标有数字0､1､2､3､……､20）移动，若遥控车最终停在“胜利大本营”（第19格），则可获得购车优惠券3万元；若遥控车最终停在“微笑大本营”（第20格），则没有任何优优惠券.已知硬币出现正､反面的概率都是，遥控车开始在第0格，客户每掷一次硬币，遥控车向前移动一次：若掷出正面，遥控车向前移动一格（从到；若掷出反面，遥控车向前移动两格（从到），直到遥控车移到“胜利大本营”或“微笑大本营”时，游戏结束.设遥控车移到第格的概率为，试证明是等比数列，并求参与游戏一次的顾客获得优惠券全额的期望值（精确到万元）.
【答案】(1)；
(2)；
(3)证明见解析，参与游戏一次的顾客获得优惠券金额的期望值为万元.
【解析】
【分析】
（1）利用直方图求平均值的公式即得；
（2）利用正态分布的性质求解即可；
（3）由题可得，利用定义证明其为等比数列，结合累加法得出的表达式，由此得到，，设参与游戏一次的顾客获得优惠券金额为万元，或0，分别求出或0的概率，然后求出期望即可.
(1)
估计这100辆汽车的单次最大续航里程的平均值为：
；
(2)
∵，
∴.
(3)
由题可知，
遥控车移到第格有两种可能：
①遥控车先到第格，又掷出反面，其概率为；
②遥控车先到第格，又掷出正面，其概率为，
∴，
∴时，，又∵，
∴当时，数列首项为，公比为的等比数列，
∴，
以上各式相加，得，
∴时，，
∴到达“胜利大本营”的概率，
∴设参与游戏一次的顾客获得优惠券金额为万元，则或0，
∴的期望，
∴参与游戏一次的顾客获得优惠券金额的期望值为万元