湖南省长郡中学2021-2022学年高二数学上学期期末试卷（Word版附解析）

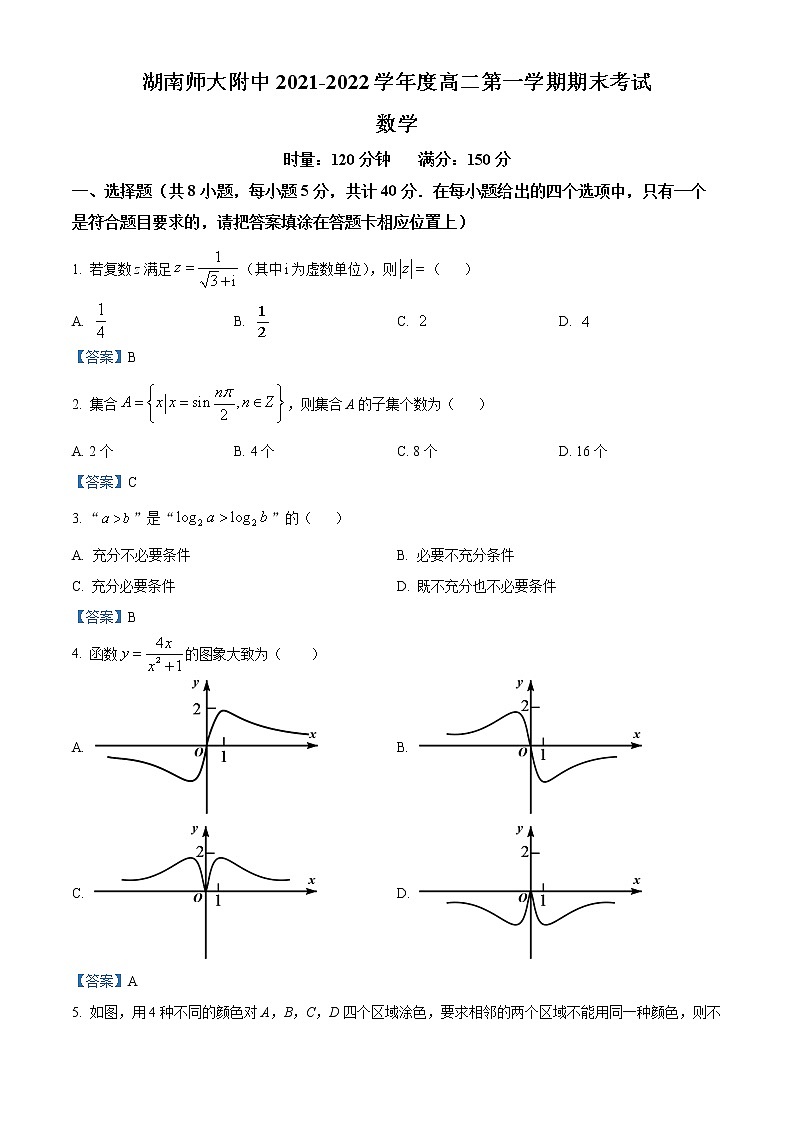
湖南师大附中2021-2022学年度高二第一学期期末考试

数学

时量：120分钟    满分：150分

一、选择题（共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案填涂在答题卡相应位置上）

1. 若复数z满足（其中为虚数单位），则（    ）

A.  B.  C.  D.

【答案】B

2. 集合，则集合A的子集个数为（    ）

A. 2个 B. 4个 C. 8个 D. 16个

【答案】C

3. “”是“”的（    ）

A. 充分不必要条件 B. 必要不充分条件

C. 充分必要条件 D. 既不充分也不必要条件

【答案】B

4. 函数的图象大致为（    ）

A.  B.

C.  D.

【答案】A

5. 如图，用4种不同的颜色对A，B，C，D四个区域涂色，要求相邻的两个区域不能用同一种颜色，则不同的涂色方法有（    ）

A. 24种 B. 48种 C. 72种 D. 96种

【答案】B

6. 双曲线（，）的一条渐近线的倾斜角为，则离心率为（    ）

A.  B.  C. 2 D. 4

【答案】C

7. 函数是偶函数且在上单调递减，，则解集为（    ）

A.  B.

C.  D.

【答案】D

8. 在正三棱锥S−ABC中，M、N分别是棱SC、BC的中点，且，若侧棱，则正三棱锥S−ABC外接球的表面积是（    ）

A.  B.  C.  D.

【答案】A

二、选择题（共4小题，每小题5分，共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，全部选对得5分，部分选对得2分，有错选得0分）

9. 对于定点P（1,2）和圆C：，下列说法正确的是（    ）

A. 圆C的半径为3

B. 过点P有两条圆的切线

C. 过点P被圆截得的弦长最大时的直线方程为

D. 圆C上存在点Q使得

【答案】BC

10. 将函数（）的图象向右平移个单位长度后得到函数的图象，则下列说法正确的是（    ）

A.

B. 函数最小正周期为

C. 函数的图象关于点（，0）成中心对称

D. 函数的一个单调递减区间为

【答案】BC

11. 如图，在棱长为的正方体中，为线段上一动点（包括端点），则以下结论正确的有（    ）

A. 三棱锥的体积为定值

B. 过点平行于平面的平面被正方体截得的多边形的面积为

C. 直线与平面所成角的正弦值的范围为

D. 当点为中点时，二面角的余弦值为

【答案】ACD

12. 设数列的前项和为，若存在实数，使得对任意，都有，则称数列为“数列”.则以下结论正确的是（    ）

A. 若是等差数列，且，公差，则数列是“数列”

B. 若是等比数列，且公比满足，则数列是“数列”

C. 若，则数列是“数列”

D. 若，则数列是“数列

【答案】BC

三、填空题（共4小题，每小题5分，共计20分．请把答案填写在答题卡相应位置上）

13. 的展开式的常数项是________．

【答案】

14. 某汽车运输公司购买了一批豪华大客车投入运营．据市场分析，每辆客车营运的总利润y（单位：10万元）与营运年数x（）为二次函数的关系（如图），则每辆客车营运年数为________时，营运的年平均利润最大．

【答案】5

15. 在△ABC中，，AB=3，，则________．

【答案】3

16. 定义方程的实数根叫做函数的“新驻点”.

（1）设，则在上的“新驻点”为___________；

（2）如果函数与的“新驻点”分别为､，那么和的大小关系是___________.

【答案】    ①.     ②.

四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）

17. 已知a，b，c分别为△ABC三个内角A，B，C的对边，，，△ABC的面积为．

（1）求a；

（2）若D为BC边上一点，且∠BAD=，求∠ADC的正弦值．

【答案】（1）   

（2）

18. 已知等差数列满足，．

（1）求的通项公式；

（2）若等比数列的前n项和为，且，，，求满足的n的最大值．

【答案】（1）   

（2）10

19. 如图，在四棱锥S−ABCD中，已知四边形ABCD是边长为的正方形，点S在底面ABCD上的射影为底面ABCD的中心点O，点P在棱SD上，且△SAC的面积为1．

（1）若点P是SD的中点，求证：平面SCD⊥平面PAC；

（2）在棱SD上是否存在一点P使得二面角P−AC−D的余弦值为？若存在，求出点P的位置；若不存在，说明理由．

【答案】（1）证明见解析   

（2）存在，点P为棱SD靠近点D的三等分点

20. 有一种鱼的身体吸收汞，当这种鱼身体中的汞含量超过其体重的1.00 ppm（即百万分之一）时，人食用它，就会对人体产生危害．现从一批该鱼中随机选出30条鱼，检验鱼体中的汞含量与其体重的比值（单位：ppm），数据统计如下：

（1）求上述数据的众数，并估计这批鱼该项数据的80%分位数；

（2）有A，B两个水池，两水池之间有8个完全相同的小孔联通，所有的小孔均在水下，且可以同时通过2条鱼．

①将其中汞的含量最低的2条鱼分别放入A水池和B水池中，若这2条鱼的游动相互独立，均有的概率进入另一水池且不再游回，求这两条鱼最终在同一水池的概率；

②将其中汞的含量最低的2条鱼都先放入A水池中，若这2条鱼均会独立地且等可能地从其中任意一个小孔由A水池进入B水池且不再游回A水池，求这两条鱼由不同小孔进入B水池的概率．

【答案】（1）众数为0. 82，8％分位数约为1.34   

（2）①；②

21. 已知点A（，0），点C为圆B：（B为圆心）上一动点，线段AC的垂直平分线与直线BC交于点G．

（1）设点G的轨迹为曲线T，求曲线T的方程；

（2）若过点P（m，0）（）作圆O：的一条切线l交（1）中的曲线T于M、N两点，求△MNO面积的最大值．

【答案】（1）   

（2）1

22. 已知函数（）．

（1）讨论函数的单调区间；

（2）若有两个极值点，（），且不等式恒成立，求实数m的取值范围．

【答案】（1）时，在递增，时，在递减，在递增   

（2）