2023年高考数学真题题库专题05 圆锥曲线中的定点问题(原卷版)

这是一份2023年高考数学真题题库专题05 圆锥曲线中的定点问题(原卷版)，共7页。试卷主要包含了多选题，单选题，解答题，填空题等内容，欢迎下载使用。
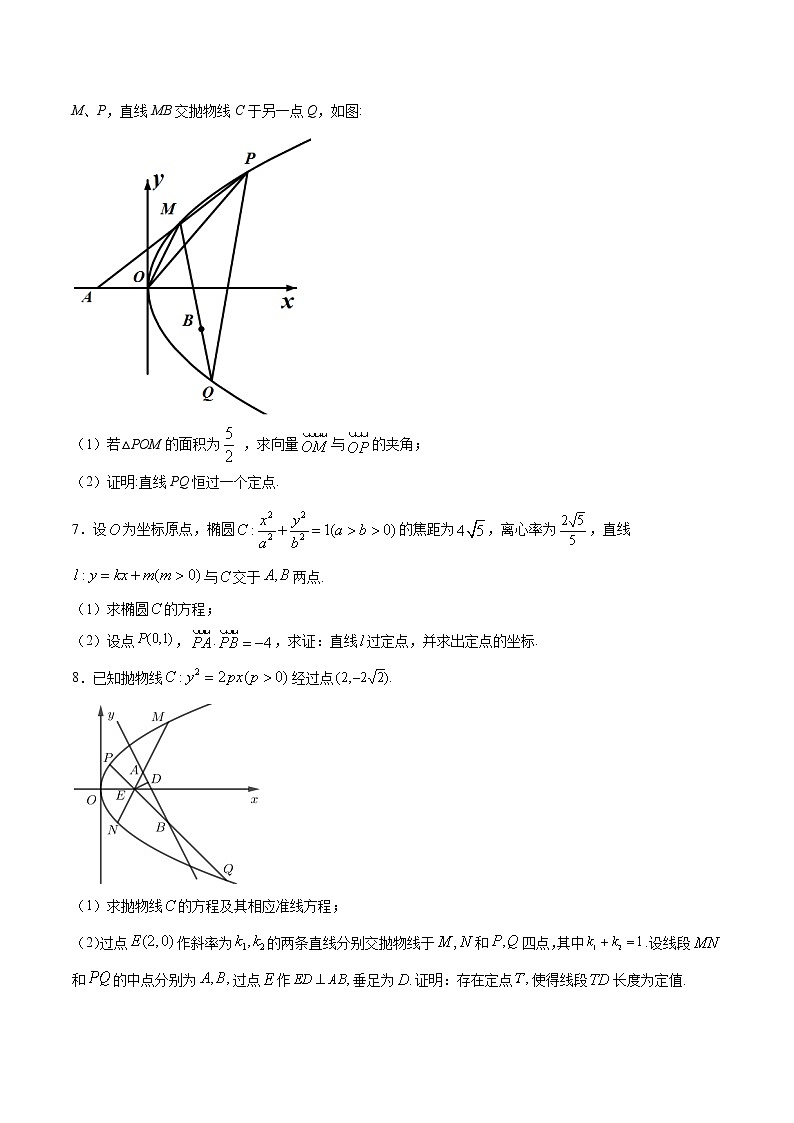
专题05 圆锥曲线中的定点问题一、多选题 1．设A，B是抛物线上的两点，是坐标原点，下列结论成立的是（    ）A．若，则B．若，直线AB过定点C．若，到直线AB的距离不大于1D．若直线AB过抛物线的焦点F，且，则2．设是抛物线上两点，是坐标原点，若，下列结论正确的为（    ）A．为定值 B．直线过抛物线的焦点C．最小值为16 D．到直线的距离最大值为4 二、单选题3．已知直线与椭圆总有公共点，则的取值范围是（    ）A． B． C． D．且三、解答题4．已知抛物线C：x2＝2py(p＞0)的焦点为F，点M(2，m)(m＞0)在抛物线上，且|MF|＝2.（1）求抛物线C的方程；（2）若点P(x0，y0)为抛物线上任意一点，过该点的切线为l0，证明：过点F作切线l0的垂线，垂足必在x轴上.5．已知抛物线E：x2＝2py(p>0)的焦点为F，A(2，y0)是E上一点，且|AF|＝2.（1）求E的方程；（2）设点B是E上异于点A的一点，直线AB与直线y＝x－3交于点P，过点P作x轴的垂线交E于点M，证明：直线BM过定点.6．已知点A（-1，0），B（1，-1）和抛物线.，O为坐标原点，过点A的动直线交抛物线C于M、P，直线MB交抛物线C于另一点Q，如图:（1）若△POM的面积为 ，求向量与的夹角；（2）证明:直线PQ恒过一个定点.7．设为坐标原点，椭圆的焦距为，离心率为，直线与交于两点.（1）求椭圆的方程；（2）设点，，求证：直线过定点，并求出定点的坐标.8．已知抛物线经过点（1）求抛物线的方程及其相应准线方程；（2）过点作斜率为的两条直线分别交抛物线于和四点，其中.设线段和的中点分别为过点作垂足为证明：存在定点使得线段长度为定值.9．设、分别是椭圆C：的左、右焦点，，直线过且垂直于x轴，交椭圆C于A、B两点，连接A、B、，所组成的三角形为等边三角形.（1）求椭圆C的方程；（2）过右焦点的直线m与椭圆C相交于M、N两点，试问：椭圆C上是否存在点P，使成立？若存在，求出点P的坐标；若不存在，说明理由.10．设椭圆的左、右焦点分别为，，离心率为，短轴长为.（1）求椭圆的标准方程；（2）设左、右顶点分别为、，点在椭圆上（异于点、），求的值；（3）过点作一条直线与椭圆交于两点，过作直线的垂线，垂足为.试问：直线与是否交于定点？若是，求出该定点的坐标，否则说明理由.11．在平面直角坐标系中，动点到点的距离和它到直线的距离的比是常数（1）求动点的轨迹方程；（2）若过点作与坐标轴不垂直的直线交动点的轨迹于两点，设点关于轴的对称点为，当直线绕着点转动时，试探究：是否存在定点，使得三点共线？若存在，求出点的坐标；若不存在，请说明理由．12．在平面直角坐标系xOy中，有三条曲线：①；②；③.请从中选择合适的一条作为曲线C，使得曲线C满足：点F(1，0)为曲线C的焦点，直线y=x-1被曲线C截得的弦长为8.（1）请求出曲线C的方程；（2）设A，B为曲线C上两个异于原点的不同动点，且OA与OB的斜率之和为1，过点F作直线AB的垂线，垂足为H，问是否存在定点M，使得线段MH的长度为定值?若存在，请求出点M的坐标和线段MH的长度；若不存在，请说明理由.13．.已知圆，点P是直线上的一动点，过点P作圆M的切线PA，PB，切点为A，B．（1）当切线PA的长度为时，求点P的坐标；（2）若的外接圆为圆N，试问：当P运动时，圆N是否过定点？若存在，求出所有的定点的坐标；若不存在，请说明理由；14．已知椭圆的一个焦点与抛物线的焦点重合，且椭圆的离心率为.（1）求椭圆的标准方程；（2）直线交椭圆于､两点，线段的中点为，直线是线段的垂直平分线，求证：直线过定点，并求出该定点的坐标.15．已知椭圆：的离心率为，且经过点，（1）求椭圆的标准方程；（2）过点作直线与椭圆相较于，两点，试问在轴上是否存在定点，使得两条不同直线，恰好关于轴对称，若存在，求出点的坐标，若不存在，请说明理由．16．已知椭圆的左、右焦点分别为、，点P在直线上且不在x轴上，直线与椭圆E的交点分别为A、B，直线与椭圆E的交点分别为C、D．（1）设直线、的斜率分别为、，求的值（2）问直线m上是否点P，使得直线OA，OB，OC，OD的斜率，，，满足若存在，求出所有满足条件的点P的坐标若不存在，请说明理由.17．已知直线l：x=my+1过椭圆C：b2x2+a2y2=a2b2(a>b>0)的右焦点F，且交椭圆C于A､B两点，点A､B在直线G：x=a2上的射影依次为点D､E.（1）若，其中O为原点，A2为右顶点，e为离心率，求椭圆C的方程；（2）连接AF，BD，试探索当m变化时，直线AE，BD是否相交于一定点N？若交于定点N，请求出N点的坐标，并给予证明；否则说明理由.18．已知抛物线的焦点为，过点的直线与抛物线在第一象限相切于点，点到坐标原点的距离为.（1）求抛物线的标准方程；（2）过点任作直线与抛物线相交于，两点，请判断轴上是否存点，使得点到直线，的距离都相等.若存在，请求出点的坐标；若不存在，请说明理由.19．已知椭圆E：的离心率为，椭圆上任一点到两个焦点的距离之和为4（1）求椭圆E的标准方程；（2）已知Q(4，0)，斜率为的直线(不过点Q)与椭圆E交于A，B两点，O为坐标原点，若，则直线是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由20．设两点的坐标分别为直线相交于点，且它们的斜率之积为，直线方程：，直线与直线分别相交于两点，交轨迹与点（1）求点的轨迹方程.（2）求证：三点共线（3）求证：以为直径的圆过定点.21．已知椭圆，以抛物线的焦点为椭圆E的一个顶点，且离心率为.（1）求椭圆E的方程；（2）若直线与椭圆E相交于A、B两点，与直线相交于Q点，P是椭圆E上一点，且满足（其中O为坐标原点），试问在x轴上是否存在一点T，使得为定值？若存在，求出点T的坐标及的值；若不存在，请说明理由.22．已知点是抛物线的准线上任意一点，过点作抛物线的两条切线、，其中、为切点.（1）证明：直线过定点，并求出定点的坐标；（2）若直线交椭圆于、两点，、分别是、的面积，求的最小值.23．已知椭圆的离心率为，其短轴长为．（1）求椭圆的标准方程；（2）已知直线，过椭圆右焦点的直线（不与轴重合）与椭圆相交于，两点，过点作，垂足为．①求证：直线过定点，并求出定点的坐标；②点为坐标原点，求面积的最大值．24．已知椭圆的左、右焦点分别为，，为椭圆上一点，且（1）求椭圆的方程（2）过点作互相垂直的两条直线分别交椭圆于另一点A，B，求证：直线AB过定点，并求出定点的坐标．25．已知椭圆：（）的左焦点，椭圆的两顶点分别为，，M为椭圆上除A，B之外的任意一点，直线MA，BM的斜率之积为.（1）求椭圆的标准方程;（2）若P为椭圆短轴的上顶点，斜率为的直线不经过P点且与椭圆交于E，F两点，设直线PE，PF的斜率分别为，且，试问直线是否过定点，若是，求出这定点；若不存在，请说明理由.四、填空题26．设抛物线上两点A，B位于x轴的同侧，且A，B两点的横坐标之积为4，则直线经过的定点坐标是______.