重庆市万州二中教育集团2022-2023学年高一数学上学期第一次质量检测（Word版附解析）

万州二中教育集团高2022级高一（上）

第一次质量检测  数学

（120分钟  150分）

注意事项：

1.答题前填写好自己的姓名、班级、考号等信息

2.请将答案正确填写在答题卡上

一.选择题：本题共8小题，每小题5分，共40分.在每小题给出的4个选项中，只有一项是符合题目要求的.

1. 若全集，集合，则（    ）

A.  B.  C.  D.

【答案】D

【解析】

【分析】根据集合的补集和交集运算可得答案.

【详解】由题得，又，所以.

故选：D.

2. 命题“”的否定是（    ）

A  B.

C.  D.

【答案】A

【解析】

【分析】利用定义写出命题的否定即可．

【详解】命题的否定是

故选：A

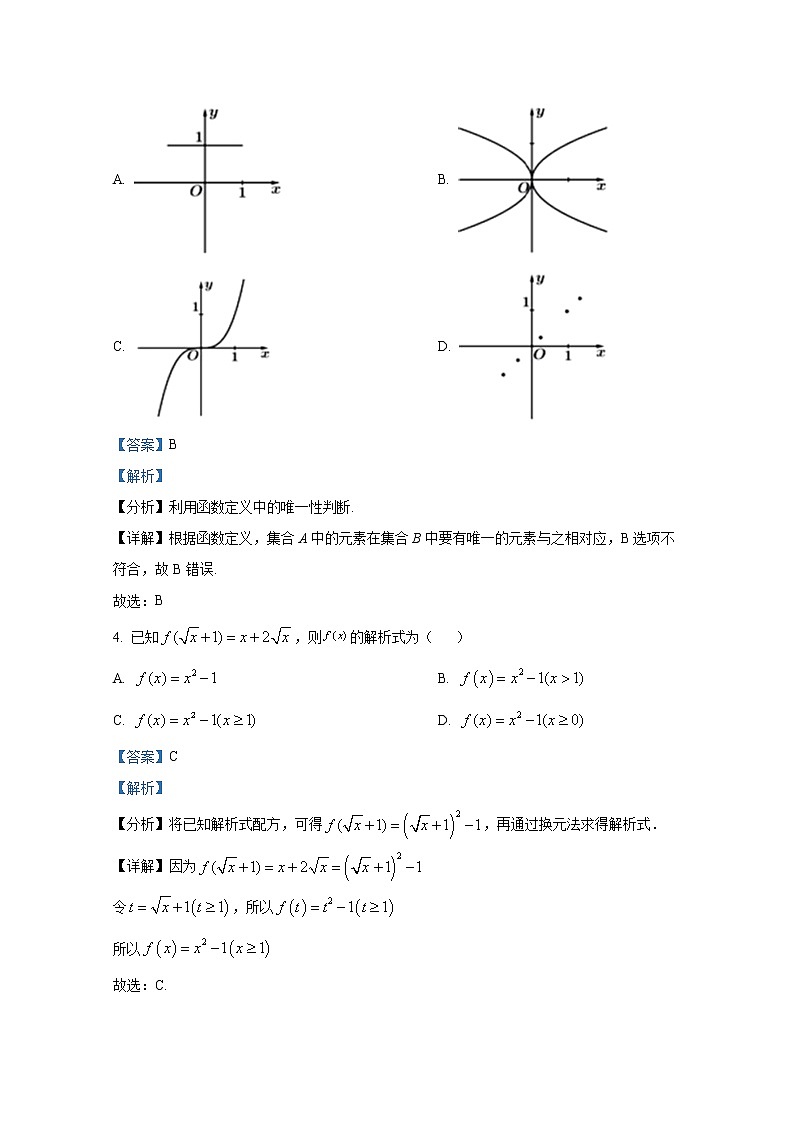
3. 如图各图中，不能表示是的函数的是（    ）

A.  B.

C.  D.

【答案】B

【解析】

【分析】利用函数定义中的唯一性判断.

【详解】根据函数定义，集合A中的元素在集合B中要有唯一的元素与之相对应，B选项不符合，故B错误.

故选：B

4. 已知，则的解析式为（    ）

A.  B.

C.  D.

【答案】C

【解析】

【分析】将已知解析式配方，可得，再通过换元法求得解析式．

【详解】因为

令，所以

所以

故选：C.

5. 已知集合，，则满足的集合的个数为（    ）

A. 4 B. 8 C. 7 D. 16

【答案】B

【解析】

【分析】根据题设列举法表示出集合，再由集合的包含关系，判断元素与集合的关系得只需讨论元素是否为集合的元素研究集合即可.

【详解】由题设，，又，

所以，只需讨论元素是否为集合的元素研究集合的个数，即可得结果，

所以集合的个数为.

故选：B

6. 已知集合，方程无实根，则“”是“”的（    ）

A. 充分不必要条件 B. 必要不充分条件

C. 充分必要条件 D. 既不充分也不必要条件

【答案】A

【解析】

【分析】首先解一元二次不等式求出集合，再根据方程无实数根求出参数的取值范围，即可得到集合，再根据集合的包含关系判断即可.

【详解】解：由，即，解得，所以，

又方程无实根，当时方程显然无解；

当时，解得，

所以，即方程无实根，

因为，

所以“”是“”的充分不必要条件；

故选：A

7. 已知，，若，则的最小值是（    ）

A. 9 B.  C.  D.

【答案】B

【解析】

【分析】根据给定条件，利用“1”的妙用求解作答.

【详解】，，，则，

所以

，当且仅当，即时取等号，

所以的最小值是.

故选：B

8. 定义，设、、是某集合的三个子集，且满足，则是的（    ）

A. 充要条件 B. 充分非必要条件

C. 必要非充分条件 D. 既非充分也非必要条件

【答案】A

【解析】

【分析】作出示意图，由可知两个阴影部分均为，根据新定义结合集合并集的运算以及充分条件与必要条件的定义判断即可.

【详解】如图，由于，

故两个阴影部分均为，

于是，

（1）若，则，，

而，

成立；

（2）反之，若，

则由于，，

，

，

，

故选：A

【点睛】本题主要考查集合并集的运算以及充分条件与必要条件的定义，考查了分类讨论、数形结合思想的应用，属于较难题.

二.多选题：本题共4小题，每小题5分，共20分.在每小题给出的4个选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. 已知，则下列不等关系正确的是 （    ）

A.  B.

C.  D.

【答案】BD

【解析】

【分析】根据不等式的性质，结合特例法进行判断即可.

【详解】A：当时，显然不成立，所以本选项不正确；

B：因，所以，

即，所以本选项正确；

C：若，显然没有意义，所以本选项不正确；

D：因为，所以，而，所以，因此本选项正确，

故选：BD

10. 下列各组函数中，两个函数是同一函数的有（    ）

A. 与 B. 与

C. 与 D. 与

【答案】ACD

【解析】

【分析】根据两个函数为同一函数的定义，对四个选项逐个分析可得答案.

【详解】对于A，，，两个函数的对应关系和定义域都相同，所以两个函数为同一函数，故A正确；

对于B，，，两个函数的定义域不同，所以两个函数不为同一函数，故B不正确；

对于C，，，两个函数的对应关系和定义域都相同，所以两个函数为同一函数，故C正确；

对于D，与的对应关系和定义域都相同，所以两个函数为同一函数，故D正确.

故选：ACD

11. 已知集合，，命题：，命题：，若是的充分不必要条件，则实数的取值范围可以是（    ）

A.  B.  C.  D.

【答案】ABD

【解析】

【分析】解一元二次不等式求集合，根据命题间的关系有，讨论、结合集合的包含关系列不等式求m的范围，即可得答案.

【详解】，

，

因为是的充分不必要条件，所以，

当时，，有（等号不同时成立），解得，

当时，，有（等号不同时成立），解得.

故选：ABD

12. 若a，，，则下列说法正确的有（    ）

A. 的最小值为4

B. 的最大值为

C. 的最小值为

D. 的最大值是

【答案】BCD

【解析】

【分析】利用基本不等式依次判断即得.

【详解】由a，，，可得，

对于A，，当且仅当，即取等号，所以，同理，故，故A错误；

对于B，∵，当且仅当，即时取等号，

∴，即的最大值为，故B正确；

对于C，，当且仅当，即时取等号，故的最小值为，故C正确；

对于D，由题可得，，

∴，

而，当且仅当，即时取等号，

∴，即的最大值是，故D正确.

故选：BCD.

三、填空题：本题共4小题，每小题5分，共20分.

13. 已知函数，那么______.

【答案】3

【解析】

【分析】由，将代入题设解析式求值即可.

【详解】.

故答案为：3

14. 不等式的解集是______.

【答案】

【解析】

【分析】不等式等价转化为或，求解集即可.

【详解】由题设，

所以或，可得或或，

故不等式解集为.

故答案为：

15. 函数，若关于的不等式的解集______.

【答案】

【解析】

【分析】根据分段函数解析式，讨论、去不等式绝对值符号求解集，然后取并集.

【详解】当时，，则，解得，故；

当时，，则，解得，故；

综上，不等式的解集为.

故答案为：.

16. 定义全集的子集的特征函数，这里表示在全集中的补集，那么对于集合、，下列所有正确说法的序号是______.

（1）    （2）

（3）    （4）

【答案】（1）（2）（4）

【解析】

【分析】

利用特征函数的定义知：（1）由，对与、关系分类讨论，可得（1）正确；利用特征函数的定义可判断（2）的正误；取特殊值情况，利用定义可判断（3）的正误；利用集合运算与函数运算可判断（4）的正误.综合可得出结论.

【详解】（1），分类讨论：

①当，则，此时；

②当，且，即，此时；

③当，且，即时，，，此时.

综合有，故（1）正确；

（2），故（2）正确；

（3）假设，任取，则，则，但，则，故（3）不正确；

（4）

，故（4）正确.

故答案为：（1）（2）（4）.

【点睛】本题考查子集与交集、并集运算转换及应用，解题时要认真审题，注意特征函数的定义的灵活运用．

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17. 设 ​.

（1）求 ​的值及​;

（2）求​.

【答案】（1）​，​，​   

（2）​

【解析】

【分析】（1）由题意得，代入方程中可求出​的值，从而可求出，

（2）先求出和，从而可求出.

【小问1详解】

因为，

所以，

所以，

解得，，

所以​

【小问2详解】

因为，

所以，，

所以.

18. 已知x＞0，y＞0，且x+y＝2．

（1）求的最小值；

（2）若4x+1﹣mxy≥0恒成立，求m的最大值．

【答案】（1）8    （2）4

【解析】

【分析】（1）由x+y＝2，得1，又x＞0，y＞0，所以（）（）＝5从而可利用基本不等式进行求解；

（2）由4x+1﹣mxy≥0恒成立可得m恒成立，又x+y＝2，所以（），结合（1）所得的结论即可确定m的最大值．

【小问1详解】

由x+y＝2，得1，又x＞0，y＞0，

所以（）（）＝55+28，

当且仅当，即x，y时等号成立，

所以的最小值为8；

【小问2详解】

由4x+1﹣mxy≥0恒成立，得m恒成立，

又x+y＝2，所以（），

由（1）可知8，所以（）≥4，当且仅当，即x，y时等号成立，

即4，故m的最大值是4．

19. 已知命题方程没有实数根.

（1）若p是真命题，求实数t的取值集合A；

（2）已知非空集合，从①充分而不必要，②必要而不充分，这两个条件中任选一个条件补充到下面问题中的横线上，并解答.

问题：是否存在实数a，使得若是的___________条件，若存在，求a的取值范围.若不存在，请说明理由.

【答案】（1）；   

（2）选① 不存在；选② 存在， .

【解析】

【分析】(1)利用一元二次方程判别式求解即可；

( 2 )选①转化为是B的真子集，列出不等式组求解；选② ，转化为是的真子集，列出不等式组求解即可.

【小问1详解】

若p是真命题，则，解得，

.

【小问2详解】

若选①，则是的真子集，

故，解得，即不存在实数a使得若是的充分不必要条件；

若选② ，则是真子集，

故，解得，

所以存在实数，满足时，是的必要不充分条件.

20. 已知函数.

（1）恒成立，求实数的取值范围；

（2）当时，求不等式的解集.

【答案】（1）   

（2）当时，不等式解集为，当时，不等式解集为，当时，不等式解集为，当时，不等式解集为.

【解析】

【分析】（1）对恒成立转化为对恒成立，讨论，并结合二次函数的图象与性质可得解；

（2）对a分情况讨论，再解不等式可得答案.

【小问1详解】

由题意得对恒成立，即对恒成立，

若，则不等式恒成立，所以满足；

若，则解得，

综上，实数的取值范围为.

【小问2详解】

当时，不等式可化为，不等式的解为，

当时，不等式可化为，

所以，

所以，

①当即时，不等式解为或，

②当即时，不等式解为，

③当即时，不等式解为或，

当时，不等式解集为，

当时，不等式解集为，

当时，不等式解集为，

当时，不等式解集为.

21. 为响应国家扩大内需的政策，某厂家拟在2021年举行促销活动，经调查测算，该产品的年销量（即该厂的年产量）x万件与年促销费用万元满足（k为常数）.如果不搞促销活动，则该产品的年销量只能是1万件.已知2021年生产该产品的固定投入为6万元，每生产1万件该产品需要再投入12万元，厂家将每件产品的销售价格定为每件产品平均成本的1.5倍（产品成本包括固定投入和再投入两部分）.

（1）将该厂家2021年该产品的利润y万元表示为年促销费用t万元的函数；

（2）该厂家2021年的年促销费用投入多少万元时厂家利润最大？

【答案】（1）；（2）该厂家2021年的年促销费用投入2.5万元时，厂家利润最大.

【解析】

【分析】（1）根据题意，当时，x=1，进而代入已知等式解出k，然后求出每件产品的销售价格，最后得到函数的解析式；

（2）根据（1）中的式子，结合基本不等式即可得到答案.

【详解】（1）由题意，当时，x=1，则，于是，所以.

（2）由（1），，

当且仅当时“=”成立.

所以，该厂家2021年的年促销费用投入2.5万元时，厂家利润最大.

22. 已知函数.

（1）求值；

（2）画出函数的图象并根据图象判断函数值域；

（3）若实数满足，则称为的二阶不动点，求函数的二阶不动点的个数.

【答案】（1）；   

（2）图象见解析，值域为；   

（3）3个.

【解析】

【分析】（1）先求出，再求的值；

（2）根据题意求出的解析式，再根据解析式画出函数图象，并根据图象可得函数的值域；

（3）由题意可得的解析式，然后分别当，和求解的解，即可得答案.

【小问1详解】

因为，

所以，

所以.

【小问2详解】

因为，

所以当时，，

当时，，

综上，

所以函数的图象如图所示，

由图象可得函数的值域为；

【小问3详解】

由题可得：

当时，由，，解得或

即函数在上有唯一的二阶不动点.

当时，由，得到方程的根为，即函数在上有唯一的二阶不动点.

当时，由，由，，解得或

即函数在上有唯一的二阶不动点.

综上所述，函数的二阶不动点有3个.