初中数学华师大版七年级上册第4章 图形的初步认识综合与测试单元测试同步训练题

第四章 图形的初步认识

【满分：120】

一、选择题：（本大题共10小题，每小题4分，共40分，给出的四个选项中，只有一项是符合题目要求的）

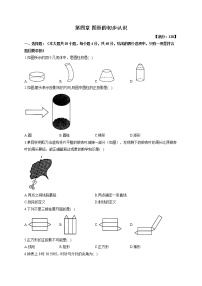
1.我国是一个农业大国，粮食的生产及储存具有悠久的历史，粮仓是储藏粮食的专用建筑物，如图所示，它可以近似看作由两个几何体组合而成的，则这两个几何体是(   )

A.三棱柱和圆柱 B.圆锥与圆柱 C.三棱柱与长方体 D.圆锥与长方体

2.如图，下午2点30分时，分针与时针所成角的度数为(   )

A.90° B.120° C.105° D.135°

3.下列几何体中,光线由上向下照射时,其正投影为三角形的是(   )

A. B. C. D.

4.某个立体图形的侧面展开图如图所示，它的底面是正三角形，那么这个立体图形是(   )

A.圆柱 B.圆锥 C.三棱柱 D.四棱柱

5.如图，在A,B两处观测到C处的方位角分别是(   )

A.北偏东65°，北偏西40°

B.北偏东65°，北偏西50°

C.北偏东25°，北偏西40°

D.北偏东25°，北偏西50°

6.如图，将一根绳子对折以后用线段AB表示，现从P处将绳子剪断，剪断后的各段绳子中最长的一段为60 cm，若，则这条绳子的原长为(   )

A.100 cm B.150 cm C.100 cm或150 cm D.120 cm或150 cm

7.如图是由5个大小相同的正方体搭成的几何体，则这个几何体的主视图是(   )

A. B. C. D.

8.小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是(   )

A. B. C. D.

9.如图，已知，，OD平分，则等于(   )

A. B. C. D.

10.如图，C为线段AD上一点，点B为CD的中点，且，.若点E在直线AD上，且，则BE的长为(   )

A.4 B.6或8 C.6 D.8

二、填空题（每小题4分，共20分）

11.如图，已知cm，cm，C为AB的中点，则线段CD的长为_________cm.

12.如图4-3-2-9，已知，，OC平分，则的度数是_____.

13.如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面_______(填字母).

14.下列图形能围成一个无盖正方体的是_____________.（填序号）

15.如图是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要___________个小立方块.

三、解答题（本大题共6小题，共计60分，解答题应写出演算步骤或证明过程）

16.（8分）观察图中的圆柱和棱柱，回答下列问题：

（1）圆柱、棱柱各由几个面组成？它们都是平的吗？

（2）圆柱的侧面与底面相交成几条线，它们都是直的吗？

（3）棱柱有几个顶点？经过每个顶点有几条棱？

17.（8分）图（1）是一个正方体，四边形APQC表示用平面截正方体的截面，其中P,Q分别是EF,FG的中点.请在图（2）中画出四边形APQC的四条边.

18.（10分）回答下列问题：

（1）如图（1），射线OC在的内部，OM平分,ON平分，若，求的度数；

（2）如图（2），射线OC,OD在的内部，OM平分,ON平分，若，，求的度数；

（3）在（2）中，，，其他条件不变，请用含m,n的代数式表示的度数（不用说理）.

19.（10分）回答下列问题：

（1）观察思考：如图，线段AB上有两个点C、D，请分别写出以点A、B、C、D为端点的线段，并计算图中共有多少条线段；

（2）模型构建：如果线段上有m个点（包括线段的两个端点），则该线段上共有多少条线段？请说明结论的正确性；

（3）拓展应用：8位同学参加班上组织的象棋比赛，比赛采用单循环制（即每两位同学之间都要进行一场比赛），那么一共要进行多少场比赛？请将这个问题转化为上述模型，并直接应用上述模型的结论解决问题.

20.（12分）在平整的地面上，由若干个完全相同的棱长为10 cm的小正方体堆成一个几何体，如图（1）所示.

（1）现已给出这个几何体的俯视图，如图（2）所示.请你画出这个几何体的主视图与左视图；

（2）若现在你手里还有一些相同的小正方体，且要保持这个几何体的主视图和俯视图不变.

①在图（1）所示的几何体上最多可以再添加几个小正方体？

②在图（1）所示的几何体中最多可以拿走几个小正方体？

③在②的情况下，把这个几何体放置在墙角，图（3）是它的俯视图，若给这个几何体露出的表面喷上红漆，则需要喷漆的面积最少是多少？

21.（12分）如图，P是线段AB上任意点， cm,C,D两点分别从P,B两点同时向A点运动，且C点的运动速度为2 cm/s,D点的运动速度为3 cm/s，设运动的时间为t s.

（1）若 cm，

①运动1 s后，求CD的长；

②当D在线段PB上运动时，试证明；

（2）如果时， cm，试探索AP的值.

答案以及解析

1.答案：B

解析：由组成几何体的特征可知，上面是圆锥，下面是圆柱，故选B.

2.答案：C

解析：下午2点30分时，时针与分针所指的位置相隔3.5个大格（钟面上每个大格为30°），故分针与时针所成角的度数为.

3.答案：C

解析：选项C是三棱柱,当光线由上向下照射时,其正投影为三角形,故选C.

4.答案：C

解析：A选项，圆柱的底面是圆，故该选项不符合题意；

B选项，圆锥的底面是圆，故该选项不符合题意；

C选项，三棱柱的底面是三角形，侧面是三个长方形，故该选项符合题意；

D选项，四棱柱的底面是四边形，故该选项不符合题意；

故选：C

5.答案：B

解析：在A处观测到C处的方位角是北偏东65°，在B处观测到C处的方位角是北偏西50°.故选B.

6.答案：C

解析：当PB的2倍最长时，得cm，cm，cm，

这条绳子的原长为cm；当AP的2倍最长时，得cm，，cm， cm，这条绳子的原长为cm.

7.答案：C

解析：从正面看该组合体，一共有三列，从左到右小正方形的个数分别为1、3、1.故选：C.

8.答案：B

解析：当等边三角形木框与光线平行时,投影是A;当等边三角形木框与光线有一定角度时,投影是C,D;投影不可能是B.故选B.

9.答案：B

解析：，，，OD平分，，.

10.答案：B

解析：若点E在线段DA的延长线上，如图（1）因为，，

所以.因为，所以.

若点E在线段AD上，如图（2），因为，，所以.

因为，所以.综上所述，BE的长为8或6.故选B.

11.答案：1

解析：cm，cm.

12.答案：

解析：，OC平分，

，

，

.

13.答案：E或C

解析：为前面,B为左面,∴①若展开图是内表面,则A为后面,D为右面,C为底面,E为上面;②若展开图是外表面,则A为后面,D为右面,E为底面,C为上面.

14.答案：①②④⑤

解析：由正方体的表面展开图可知，①②④⑤可以折叠成无盖的正方体，而③⑥折叠成的是有两面重合的图形.

15.答案：54

解析：由俯视图易得最底层有7个小立方块,第二层有2个小立方块,第三层有1个小立方块,那么共有7+2+1=10(个)小立方块组成.若搭成一个大正方体,共需4×4×4=64(个)小立方块,所以还需64-10=54(个)小立方块.

16.答案：解：（1）圆柱由3个面组成，其中有一个面是曲面；棱柱由8个面组成，都是平的；

（2）圆柱的侧面与底面相交成2条线，它们是曲线；

（3）棱柱共有12个顶点，经过每个顶点有3条棱.

17.答案：画出四边形APQC的四条边如下图所示：

18.答案：（1）因为OM平分，所以，同理.

因为，所以.

（2）因为OM平分，所以，同理可得，

所以

.

因为，，所以.

（3）由（2）得.

19.答案：（1）以点A为左端点的线段有线段AB、AC、AD，以点C为左端点的线段有线段CD、CB，以点D为左端点的线段有线段DB，

共有条线段.

（2）.

理由：设如果线段上有m个点，则该线段上共有线段x条，

则，

，

，.

（3）把8位同学看作直线上的8个点，每两位同学之间的一场比赛看作一条线段，

直线上8个点所构成的线段条数就等于比赛的场数，

因此一共要进行场比赛.

20.答案：（1）主视图和左视图如图所示：

（2）①最多可以再添加2个小正方体.

②最多可以拿走2个小正方体.

③小正方体每一个面的面积是，且②中拿走几何体的第二行，最左侧上方的两个小正方体，此时几何体露出的表面最少，所以需要喷漆的面积最少是.解析：

21.答案：（1）①由题意可知（cm），（cm）.

因为 cm, cm，所以 cm，

所以（cm）.

②由题意得 cm, cm.因为 cm, cm，

所以 cm, cm，所以 cm，

所以 cm.

因为，所以.

（2）当时，（cm），（cm）.

当点D在点C的右边时，如图所示：

因为 cm，所以 cm，所以 cm，

所以 cm.

当点D在点C的左边时，如图所示：

cm所以 cm.

综上所述，AP的值为9 cm或11 cm.