

福建省厦门市思明区双十中学2022-2023学年八年级上学期期中数学试卷 (含答案)
展开2022-2023学年福建省厦门市思明区双十中学八年级第一学期期中数学试卷
一、选择题(本大题有10小题,每小题4分,共40分.每小题都有四个选项,其中有且只有一个选项正确)
1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B. C. D.
2.计算m3•m2的结果,正确的是( )
A.m2 B.m3 C.m5 D.m6
3.如图,小华为估计水塘边A,B两点间的距离,在池塘同侧选取一点O,测出点O与点A间的距离为15米,点O与点B间的距离为10米,则AB长可能是( )
A.5米 B.15米 C.25米 D.30米
4.一个n边形的内角和为720°,则n等于( )
A.4 B.5 C.6 D.7
5.如图,直线m∥n,点A在直线m上,点B、C在直线n上,AB=CB,∠2=40°,则∠1等于( )
A.70° B.60° C.50° D.40°
6.()2020×(﹣3)2021的计算结果是( )
A.3 B.﹣3 C. D.﹣
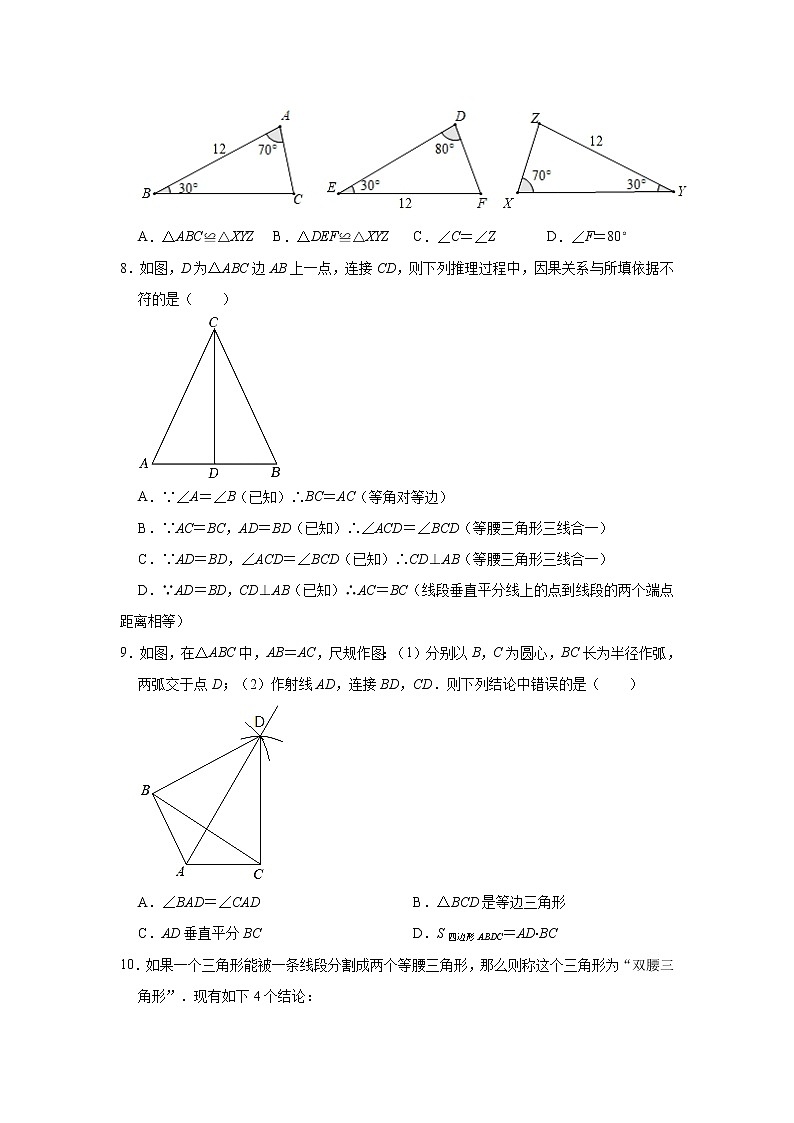
7.已知,△ABC,△DEF,△XYZ的相关数据如图所示,则( )
A.△ABC≌△XYZ B.△DEF≌△XYZ C.∠C=∠Z D.∠F=80°
8.如图,D为△ABC边AB上一点,连接CD,则下列推理过程中,因果关系与所填依据不符的是( )
A.∵∠A=∠B(已知)∴BC=AC(等角对等边)
B.∵AC=BC,AD=BD(已知)∴∠ACD=∠BCD(等腰三角形三线合一)
C.∵AD=BD,∠ACD=∠BCD(已知)∴CD⊥AB(等腰三角形三线合一)
D.∵AD=BD,CD⊥AB(已知)∴AC=BC(线段垂直平分线上的点到线段的两个端点距离相等)
9.如图,在△ABC中,AB=AC,尺规作图:(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D;(2)作射线AD,连接BD,CD.则下列结论中错误的是( )
A.∠BAD=∠CAD B.△BCD是等边三角形
C.AD垂直平分BC D.S四边形ABDC=AD⋅BC
10.如果一个三角形能被一条线段分割成两个等腰三角形,那么则称这个三角形为“双腰三角形”.现有如下4个结论:
①若一个三角形的两个内角分别是36°、72°,则这个三角形是“双腰三角形”
②若一个三角形是直角三角形,则这个三角形是“双腰三角形”
⑧若一个三角形的一个内角是另一个内角的2倍,则这个三角形一定是“双腰三角形”
④若一个三角形的一个内角是另一个内角的3倍,则这个三角形一定是“双腰三角形”
其中正确的个数为( )
A.1 B.2 C.3 D.4
二、填空题(本大题有6小题,第11题每空2分,其余每题4分,共26分)
11.化简:(1)﹣a+a= ;(2)(x4)2= ;(3)(﹣2a2b)3= .
12.平面直角坐标系中,点P(3,1)关于x轴对称的点的坐标是 .
13.如图,在四边形ABCD中,∠A=90°,AD=3,对角线BD平分∠ABC,则点D到BC的距离为 .
14.在△ABC中,∠ACB=90°,AC=BC,AB=5,则AB边上中线的长为 .
15.如图,点F在正五边形ABCDE的内部,△ABF为等边三角形,连接EF,则∠AEF的度数为 .
16.如图,点M在等边△ABC的边BC上,BM=8,射线CD⊥BC垂足为点C,点P是射线CD上一动点,点N是线段AB上一动点,当MP+NP的值最小时,BN=9,则AC的长为 .
三、解答题(本题有9小题,共84分)
17.计算:x4•x2﹣(3x3)2.
18.如图,点A、D、C、F在同一条直线上,BC=EF,AD=CF,AB=DE.求证:△ABC≌△DEF.
19.如图,△ABC在平面直角坐标系中,其顶点坐标如下:A(﹣3,1),B(﹣1,﹣2),C(1,3).
(1)作出△ABC关于y轴对称的图形△A1B1C1.其中 A、B、C分别和A1、B1、C1对应,则线段AA1的长度为 :
(2)仅用直尺在x轴上确定点P的位置:使得点P到点A、点C的距离之和最小.
20.如图,在Rt△ABC中,∠C=90°,∠B=30°,AD平分∠BAC交BC于点D.
(1)求证:点D在AB的垂直平分线上;
(2)若CD=2,求BD的长.
21.如图,在△ABC中,AC=2AB.
(1)尺规作图:作∠BAC的平分线AD,交BC于点E;作线段AC的垂直平分线交AC于点F,交AD于点G;连接BG,CG(不写作法,保留作图痕迹);
(2)在(1)的条件下,证明:AB⊥BG.
22.如图,在△ABC中,AB=AC,D为CA延长线上一点,且DE⊥BC交AB于点F.
(1)求证:△ADF是等腰三角形;
(2)EF=4,F为AB中点,求DF的长.
23.在综合实践课上,老师以“含30°的三角板和等腰三角形纸片”为模具与同学们开展如下数学活动;
在等腰三角形纸片ABC中,CA=CB,∠ACB=120°,将一块含30°角的足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图所示放置,顶点P在线段AB上滑动(点P不与A,B重合),三角尺的直角边PM始终经过点C,并与CB的夹角为α(∠PCB=α),斜边PN交AC于点D.
(1)特例感知
当∠BPC=110°时,α= °,点P从B向A运动时,∠ADP逐渐变 (填“大”或“小”);
(2)思维拓展
在点P的滑动过程中,△PCD的形状可以是等腰三角形吗?若可以,请求出夹角α的大小;若不可以,请说明理由.
24.如图,在平面直角坐标系中,A(﹣3,0)、C(7,0),B为y轴正半轴上一点,D在第四象限.若BC⊥CD,CA平分∠BCD,∠ABC+∠ADC=180°.
(1)直接写出B点坐标( , );
(2)求证:AB=AD;
(3)求四边形ABCD的面积.
25.如图1,在等边△ABC中,D,E分别是边AC,BC上一点,且AD=CE,BD与AE相交于点M.
(1)求证:△ABD≌△CAE;
(2)求证:∠AMD=60°;
(3)如图2,连接CM,当BM=2AM时,求证:CM⊥BM.
参考答案
一、选择题(本大题有10小题,每小题4分,共40分.每小题都有四个选项,其中有且只有一个选项正确)
1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B. C. D.
【分析】根据轴对称图形的概念对各选项分析判断利用排除法求解.
解:A、是轴对称图形,故本选项正确;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误.
故选:A.
2.计算m3•m2的结果,正确的是( )
A.m2 B.m3 C.m5 D.m6
【分析】利用同底数幂的乘法的法则进行运算即可.
解:m3•m2
=m3+2
=m5.
故选:C.
3.如图,小华为估计水塘边A,B两点间的距离,在池塘同侧选取一点O,测出点O与点A间的距离为15米,点O与点B间的距离为10米,则AB长可能是( )
A.5米 B.15米 C.25米 D.30米
【分析】应用三角形三边的关系,两边之和大于第三边两边之差小于第三边,进行计算即可得出答案.
解:根据题意可得,
15﹣10<AB<15+10,
即:5<AB<25.
∴AB长可能是15米.
故选:B.
4.一个n边形的内角和为720°,则n等于( )
A.4 B.5 C.6 D.7
【分析】多边形的内角和可以表示成(n﹣2)•180°,依此列方程可求解.
解:依题意有:
(n﹣2)•180°=720°,
解得n=6.
故答案为:C.
5.如图,直线m∥n,点A在直线m上,点B、C在直线n上,AB=CB,∠2=40°,则∠1等于( )
A.70° B.60° C.50° D.40°
【分析】根据平行线的性质求出∠ABC=∠2=40°,根据等腰三角形的性质得出∠BCA=70°,根据平行线的性质即可得解.
解:∵m∥n,∠2=40°,
∴∠ABC=∠2=40°,∠1=∠BCA,
∵AB=CB,
∴∠BAC=∠BCA=×(180°﹣∠ABC)=70°,
∴∠1=70°,
故选:A.
6.()2020×(﹣3)2021的计算结果是( )
A.3 B.﹣3 C. D.﹣
【分析】利用积的乘方的法则进行运算即可.
解:()2020×(﹣3)2021
=()2020×(﹣3)2020×(﹣3)
=(﹣)2020×(﹣3)
=(﹣1)2020×(﹣3)
=1×(﹣3)
=﹣3.
故选:B.
7.已知,△ABC,△DEF,△XYZ的相关数据如图所示,则( )
A.△ABC≌△XYZ B.△DEF≌△XYZ C.∠C=∠Z D.∠F=80°
【分析】根据全等三角形的判定方法对A、B选项进行判断;根据三角形内角和定理对C、D选项进行判断.
解:∵∠A=∠X,∠B=∠Y,
而AB≠XY,
∴不能判断△ABC≌△XYZ;所以A选项不符合题意;
在△XYZ中,∠Z=180°﹣∠X﹣∠Y=180°﹣70°﹣30°=80°,
∵∠D=∠Z,
而EF≠XY,
∴不能判断△DEF≌△XYZ;所以B选项不符合题意;
在△ABC中,∠C=180°﹣∠A﹣∠B=180°﹣70°﹣30°=80°,
∴∠C=∠Z,所以C选项符合题意;
在△DEF中,∠F=180°﹣∠D﹣∠E=180°﹣80°﹣30°=70°,所以D选项不符合题意.
故选:C.
8.如图,D为△ABC边AB上一点,连接CD,则下列推理过程中,因果关系与所填依据不符的是( )
A.∵∠A=∠B(已知)∴BC=AC(等角对等边)
B.∵AC=BC,AD=BD(已知)∴∠ACD=∠BCD(等腰三角形三线合一)
C.∵AD=BD,∠ACD=∠BCD(已知)∴CD⊥AB(等腰三角形三线合一)
D.∵AD=BD,CD⊥AB(已知)∴AC=BC(线段垂直平分线上的点到线段的两个端点距离相等)
【分析】根据等角对等边以及等腰三角形的三线合一定理、线段垂直平分线的性质逐一判断即可得到答案.
解:A.∵∠A=∠B(已知),
∴BC=AC(等角对等边),
因果关系与所填依据相符,不符合题意;
B.∵AC=BC,AD=BD(已知),
∴∠ACD=∠BCD(等腰三角形三线合一),
因果关系与所填依据相符,不符合题意;
C.∵AD=BD,∠ACD=∠BCD(已知),
∴CD⊥AB(等腰三角形三线合一),
因为条件没有等腰三角形,故因果关系与所填依据不符,符合题意;
D.∵AD=BD,CD⊥AB(已知),
∴AC=BC(线段垂直平分线上的点到线段的两个端点距离相等),
因果关系与所填依据相符,不符合题意;
故选:C.
9.如图,在△ABC中,AB=AC,尺规作图:(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D;(2)作射线AD,连接BD,CD.则下列结论中错误的是( )
A.∠BAD=∠CAD B.△BCD是等边三角形
C.AD垂直平分BC D.S四边形ABDC=AD⋅BC
【分析】根据作图方法可得BC=BD=CD,进而可得△BCD是等边三角形,再利用垂直平分线的判定方法可得AD垂直平分BC,利用等腰三角形的性质可得∠BAD=∠CAD,利用面积公式可计算四边形ABDC的面积.
解:根据作图方法可得BC=BD=CD,
∵BD=CD,
∴点D在BC的垂直平分线上,
∵AB=AC,
∴点A在BC的垂直平分线上,
∴AD是BC的垂直平分线,故C结论正确;
∴O为BC中点,
∴AO是△BAC的中线,
∵AB=AC,
∴∠BAD=∠CAD,故A结论正确;
∵BC=BD=CD,
∴△BCD是等边三角形,故B结论正确;
∵四边形ABDC的面积=S△BCD+S△ABC=BC•DO+BC•AO=BC•AD,故D选项错误,
故选:D.
10.如果一个三角形能被一条线段分割成两个等腰三角形,那么则称这个三角形为“双腰三角形”.现有如下4个结论:
①若一个三角形的两个内角分别是36°、72°,则这个三角形是“双腰三角形”
②若一个三角形是直角三角形,则这个三角形是“双腰三角形”
⑧若一个三角形的一个内角是另一个内角的2倍,则这个三角形一定是“双腰三角形”
④若一个三角形的一个内角是另一个内角的3倍,则这个三角形一定是“双腰三角形”
其中正确的个数为( )
A.1 B.2 C.3 D.4
【分析】根据“双腰三角形”的定义,指出分割线即可.
解:①根据三角形内角和为180°,可以求出第三个角为72°,即为等腰三角形,
作一个底角的角平分线,该线把三角形分成两个等腰三角形,故结论①正确;
②连接直角顶点和斜边中点,根据直角三角形斜边中线等于斜边的一半,即这条线段把三角形分成两个等腰三角形.故结论②正确;
③如图,∠C=α,∠A=2α,
作∠DBC=α,交AC于D,
∵∠ADB=∠C+∠DBC=2α=∠A,
∴BD分成的两个三角形都是等腰三角形,故结论③正确;
④如图,设∠C=α,∠ABC=3α,
作BC的中垂线交AC于D,连接BD,则BD=DC,
∴∠DBC=∠C=α,
由三角形外角的性质可知,∠ADB=2α,
而∠ABD=3α﹣α=2α,
∴两个三角形都是等腰三角形,故结论④正确.
故选:D.
二、填空题(本大题有6小题,第11题每空2分,其余每题4分,共26分)
11.化简:(1)﹣a+a= 0 ;(2)(x4)2= x8 ;(3)(﹣2a2b)3= ﹣8a6b3 .
【分析】(1)利用合并同类项的法则运算即可;
(2)利用幂的乘方的法则进行运算即可;
(3)利用积的乘方的法则进行运算即可.
解:(1)﹣a+a
=(﹣1+1)a
=0;
故答案为:0;
(2)(x4)2
=x4×2
=x8;
故答案为:x8;
(3)(﹣2a2b)3
=(﹣2)3×(a2)3b3
=﹣8a6b3.
故答案为:﹣8a6b3.
12.平面直角坐标系中,点P(3,1)关于x轴对称的点的坐标是 (3,﹣1) .
【分析】直接利用关于x轴对称点的性质(横坐标不变,纵坐标互为相反数)解答即可.
解:平面直角坐标系中,点P(3,1)关于x轴对称的点的坐标是(3,﹣1).
故答案为:(3,﹣1).
13.如图,在四边形ABCD中,∠A=90°,AD=3,对角线BD平分∠ABC,则点D到BC的距离为 3 .
【分析】由∠A=90°,AD=3可得点D到AB距离等于3,再由BD平分∠ABC及角平分线的的性质求解.
解:∵BD为∠ABC的角平分线,
∴点D到AB,BC的距离相等,
∵∠A=90°,AD=3,
∴点D到BC的距离为3,
故答案为:3.
14.在△ABC中,∠ACB=90°,AC=BC,AB=5,则AB边上中线的长为 .
【分析】根据等腰直角三角形的性质得出AD=DB,进而利用等腰三角形的性质得出CD,进而利用勾股定理解答即可.
解:如图:CD是AB边上中线,
∵∠ACB=90°,AC=BC,AB=5,
∴AD=BD=AB=,
∵CD⊥AB,∠ACD=∠BCD==45°,
∴∠A=∠ACD=45°,
∴AD=CD=.
故答案为:.
15.如图,点F在正五边形ABCDE的内部,△ABF为等边三角形,连接EF,则∠AEF的度数为 66° .
【分析】根据等边三角形的性质得到AF=BF=AB,∠AFB=∠ABF=60°,由正五边形的性质得到AB=AE,∠BAE=108°,等量代换得到AF=AE,∠FAE=48°,根据三角形的内角和即可得到结论.
解:∵△ABF是等边三角形,
∴AF=BF=AB,∠AFB=∠BAF=60°,
在正五边形ABCDE中,AB=AE,∠BAE==108°,
∴AF=AE,∠FAE=∠BAE﹣∠BAF=48°,
∴∠AEF=(180°﹣∠FAE)=66°.
故答案为:66°.
16.如图,点M在等边△ABC的边BC上,BM=8,射线CD⊥BC垂足为点C,点P是射线CD上一动点,点N是线段AB上一动点,当MP+NP的值最小时,BN=9,则AC的长为 13 .
【分析】根据等边三角形的性质得到AC=BC,∠B=60°,作点M关于直线CD的对称点G,过G作GN⊥AB于N,交CD于P,则此时,MP+PN的值最小,根据直角三角形的性质得到BG=2BN=18,求得MG=10,于是得到结论.
解:∵△ABC是等边三角形,
∴AC=BC,∠B=60°,
作点M关于直线CD的对称点G,过G作GN⊥AB于N,交CD于P,
则此时,MP+PN的值最小,
∵∠B=60°,∠BNG=90°,
∴∠G=30°,
∵BN=9,
∴BG=2BN=18,
∴MG=10,
∴CM=CG=5,
∴AC=BC=13,
故答案为:13.
三、解答题(本题有9小题,共84分)
17.计算:x4•x2﹣(3x3)2.
【分析】先算同底数幂的乘法,积的乘方,再合并同类项即可.
解:x4•x2﹣(3x3)2
=x6﹣9x6
=﹣8x6.
18.如图,点A、D、C、F在同一条直线上,BC=EF,AD=CF,AB=DE.求证:△ABC≌△DEF.
【分析】由AD=CF,根据等式性质得AC=DF,再根据SSS定理得到结论.
【解答】证明:∵AD=CF,
∴AD+DC=CF+DC,
即AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
19.如图,△ABC在平面直角坐标系中,其顶点坐标如下:A(﹣3,1),B(﹣1,﹣2),C(1,3).
(1)作出△ABC关于y轴对称的图形△A1B1C1.其中 A、B、C分别和A1、B1、C1对应,则线段AA1的长度为 6 :
(2)仅用直尺在x轴上确定点P的位置:使得点P到点A、点C的距离之和最小.
【分析】(1)根据轴对称变换的性质找出对应点即可求解,根据图象直接得出AA1的长度;
(2)作点A关于x轴的对称点A',连接A'C交x轴于点P,则点P即为所求.
解:如图所示,△A1B1C1即为所求,线段AA1的长度为6,
故答案为:6;
(2)点P的位置如图所示.
20.如图,在Rt△ABC中,∠C=90°,∠B=30°,AD平分∠BAC交BC于点D.
(1)求证:点D在AB的垂直平分线上;
(2)若CD=2,求BD的长.
【分析】(1)根据题意和角平分线的定义,可以得到∠B和∠BAD的关系,然后即可得到BD和AD的关系,再根据线段垂直平分线的性质,即可证明结论成立;
(2)根据30°角所对的直角边和斜边的关系,可以得到BD的长.
【解答】(1)证明:∵∠C=90°,∠B=30°,AD平分∠BAC,
∴∠BAC=60°,∠DAB=30°,
∴∠B=∠BAD,
∴DB=DA,
∴点D在AB的垂直平分线上;
(2)解:∵∠C=90°,∠B=30°,AD平分∠BAC,
∴∠BAC=60°,∠DAC=30°,
∵CD=2,
∴AD=4,
由(1)知:BD=AD,
∴BD=4.
21.如图,在△ABC中,AC=2AB.
(1)尺规作图:作∠BAC的平分线AD,交BC于点E;作线段AC的垂直平分线交AC于点F,交AD于点G;连接BG,CG(不写作法,保留作图痕迹);
(2)在(1)的条件下,证明:AB⊥BG.
【分析】(1)根据要求作出图形即可;
(2)证明△AGB≌△AGF,可得结论.
【解答】(1)解:图形如图所示:
(2)证明:由作图可知AF=FC,∠AFG=90°,∠BAG=∠FAG,
∵AC=2AB,
∴AB=AF,
在△AGB和△AGF中,
,
∴△AGF≌△AGB(SAS),
∴∠AFG=∠ABG=90°,
∴AB⊥BG.
22.如图,在△ABC中,AB=AC,D为CA延长线上一点,且DE⊥BC交AB于点F.
(1)求证:△ADF是等腰三角形;
(2)EF=4,F为AB中点,求DF的长.
【分析】(1)利用等腰三角形的性质可得∠B=∠C,再利用等角的余角相等证明∠D=∠AFD即可解答;
(2)由(1)得△ADF是等腰三角形,想到等腰三角形的三线合一性质,所以过点A作AG⊥DE,垂足为G,先在Rt△BEF中,利用勾股定理求出EF的长,然后证明△AGF≌△BEF即可解答.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠DEC=∠DEB=90°,
∴∠B+∠BFE=90°,∠C+∠D=90°,
∴∠D=∠BFE,
∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴AD=AF,
∴△ADF是等腰三角形;
(2)过点A作AG⊥DE,垂足为G,
∵AB=AC,EF=4,
∴BF2=BE2+EF2,
∵F为AB中点,
∴AF=BF=AB,
在Rt△BFE和△AFG中,
∵∠AGF=∠BEF=90°,∠AFG=∠BFE,
∴△AFG≌△BFE(AAS),
∴GF=EF=4,
∵AD=AF,AG⊥DF,
∴DF=2GF=8.
23.在综合实践课上,老师以“含30°的三角板和等腰三角形纸片”为模具与同学们开展如下数学活动;
在等腰三角形纸片ABC中,CA=CB,∠ACB=120°,将一块含30°角的足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图所示放置,顶点P在线段AB上滑动(点P不与A,B重合),三角尺的直角边PM始终经过点C,并与CB的夹角为α(∠PCB=α),斜边PN交AC于点D.
(1)特例感知
当∠BPC=110°时,α= 40 °,点P从B向A运动时,∠ADP逐渐变 小 (填“大”或“小”);
(2)思维拓展
在点P的滑动过程中,△PCD的形状可以是等腰三角形吗?若可以,请求出夹角α的大小;若不可以,请说明理由.
【分析】(1)根据等腰三角形的性质可得∠B=30°,进而可以解决问题;
(2)点P在滑动时,△PCD的形状可以是等腰三角形,分三种情况考虑:当PC=PD;PD=CD;PC=CD,分别求出夹角α的大小即可.
解:(1)当∠BPC=110°时,α=40°,点P从B向A运动时,∠ADP逐渐变小.
理由如下:
∵CA=CB,∠ACB=120°,
∴∠B=30°,
∴α=180°﹣110°﹣30°=40°;
故答案为:40,小;
(2)∵△PCD是等腰三角形,
∠PCD=120°﹣α,∠CPD=30°,
①当PC=PD时,
∴∠PCD=∠PDC=(180°﹣30°)=75°,
即120°﹣α=75°,
∴∠α=45°;
②当PD=CD时,△PCD是等腰三角形,
∴∠PCD=∠CPD=30°,即120°﹣α=30°,
∴α=90°;
③当PC=CD时,△PCD是等腰三角形,
∴∠CDP=∠CPD=30°,
∴∠PCD=180°﹣2×30°=120°,
即120°﹣α=120°,
∴α=0°,
此时点P与点B重合,点D和A重合,
∵点P不与A,B重合,
∴α=0°,舍去,
综合所述:当△PCD是等腰三角形时,α=45°或90°.
24.如图,在平面直角坐标系中,A(﹣3,0)、C(7,0),B为y轴正半轴上一点,D在第四象限.若BC⊥CD,CA平分∠BCD,∠ABC+∠ADC=180°.
(1)直接写出B点坐标( 0 , 7 );
(2)求证:AB=AD;
(3)求四边形ABCD的面积.
【分析】(1)证明△OBC是等腰直角三角形,可得结论;
(2)过点A作AM⊥BC于点M,AN⊥CD,交CD的延长线于点N.证明△AMB≌△AND(AAS),可得结论;
(3)证明四边形AMCN是正方形,再证明四边形ABCD的面积=正方形AMCN的面积即可.
【解答】(1)解:∵C(7,0),
∴OC=7,
∵BC⊥CD,
∴∠BCD=90°,
∵AC平分∠BCD,
∴∠BCA=∠ACD=45°,
∵∠COB=90°,
∴∠OBC=∠OCB=45°,
∴OB=OC=7,
∴B(0,7),
故答案为:0,7;
(2)证明:过点A作AM⊥BC于点M,AN⊥CD,交CD的延长线于点N.
∵AC平分∠BCD,
∴AM=AN,
∵∠ABM+∠ADC=180°,∠ADN+∠ADC=180°,
∴∠ABM=∠ADN,
∵∠AMB=∠N=90°,
∴△AMB≌△AND(AAS),
∴AB=AD;
(3)解:∵A(﹣3,0),B(7,0),
∴OA=3,OC=7,
∴AC=10,
∵AM⊥CM,∠ACM=45°,
∴AM=CM=5,
∵△AMB≌△AND,
∴S△AMB=S△AND,
∴S四边形ABCD=S四边形AMCN,
∵∠AMC=∠MCN=∠N=90°,
∴四边形AMCN是矩形,
∵AM=CM,
∴四边形AMCN是正方形,
∴S四边形ABCD=S四边形AMCN=(5)2=50.
25.如图1,在等边△ABC中,D,E分别是边AC,BC上一点,且AD=CE,BD与AE相交于点M.
(1)求证:△ABD≌△CAE;
(2)求证:∠AMD=60°;
(3)如图2,连接CM,当BM=2AM时,求证:CM⊥BM.
【分析】(1)由SAS证明△ABD≌△CAE即可;
(2)由全等三角形的性质得得∠ABD=∠CAE,再由三角形的外角性质即可得出结论;
(3)延长BD到F,使AM=MF,连接AF、CF,证△BAM≌△CAF(SAS),得BM=CF,∠AFC=∠AMB=120°,则CF=2AM=2AF=2MF,取CF的中点N,连接MN,则FN=NC=MF,然后证△FMN是等边三角形,得MN=FN=CN,∠FMN=60°,即可解决问题.
【解答】证明:(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=∠ABC=60°,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(SAS);
(2)由(1)可知,△ABD≌△CAE,
∴∠ABD=∠CAE,
∴∠AMD=∠ABD+∠BAE=∠CAE+∠BAE=∠BAC=60°;
(3)如图2,延长BD到F,使AM=MF,连接AF、CF,
由(1)知:∠AMF=60°,
∴△AMF是等边三角形,
∴AM=AF,∠AFM=∠MAF=60°,
∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
∴∠BAM=∠CAF,
在△BAM和△CAF中,
,
∴△BAM≌△CAF(SAS),
∴BM=CF,∠AFC=∠AMB=180°﹣∠AMF=120°,
∵BM=2AM,
∴CF=2AM=2AF=2MF,
取CF的中点N,连接MN,则FN=NC=MF,
∵∠AFM=60°,
∴∠MFN=∠AFC﹣∠AFM=120°﹣60°=60°,
∴△FMN是等边三角形,
∴MN=FN=CN,∠FMN=60°,
∴∠NMC=∠NCM,
∵∠FNM=∠NMC+∠NCM=60°,
∴∠NMC=30°,
∴∠CMF=∠FMN+∠NMC=60°+30=90°,
∴BM⊥CM.
2023-2024学年福建省厦门市思明区双十中八年级(上)期中数学试卷(含解析): 这是一份2023-2024学年福建省厦门市思明区双十中八年级(上)期中数学试卷(含解析),共34页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年福建省厦门市思明区双十中学八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年福建省厦门市思明区双十中学八年级(下)期末数学试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年福建省厦门市思明区双十中学八年级(下)期中数学试卷(含解析): 这是一份2022-2023学年福建省厦门市思明区双十中学八年级(下)期中数学试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












