中考数学复习第14讲二次函数的应用精练课件

这是一份中考数学复习第14讲二次函数的应用精练课件，共24页。

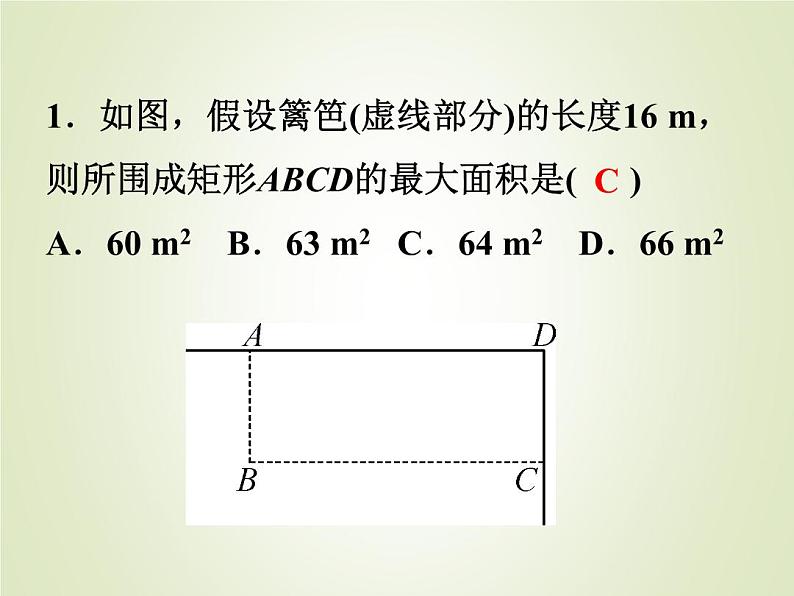
1．如图，假设篱笆(虚线部分)的长度16 m，则所围成矩形ABCD的最大面积是( )A．60 m2 B．63 m2 C．64 m2 D．66 m2
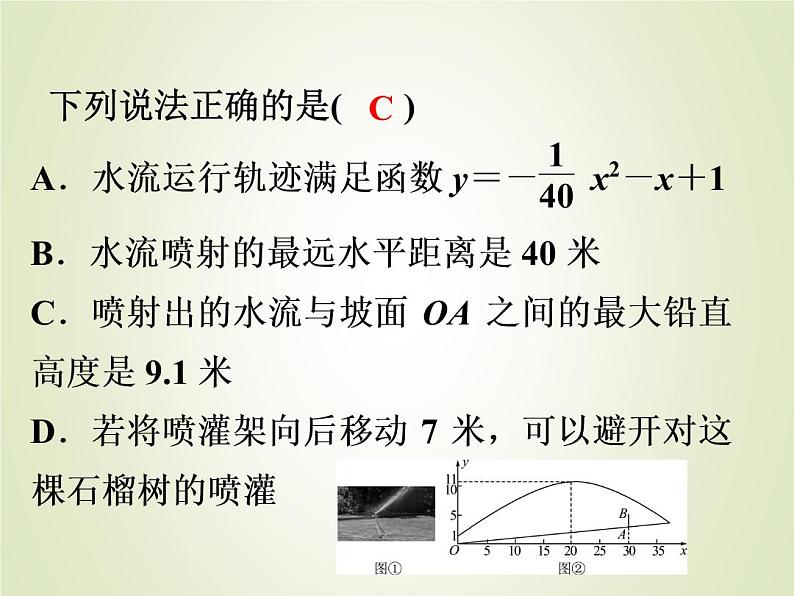
3．如图①，一个移动喷灌架喷射出的水流可以近似地看成抛物线．图②是喷灌架为一坡地草坪喷水的平面示意图，喷水头的高度(喷水头距喷灌架底部的距离)是1米．当喷射出的水流距离喷水头20米时，达到最大高度11米，现将喷灌架置于坡度为1∶10的坡地底部点O处，草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB，因为刚刚被喷洒了农药，近期不能被喷灌．
下列说法正确的是( )
4．(2021·沈阳)某超市购进一批单价为8元的生活用品，如果按每件9元出售，那么每天可销售20件．经调查发现，这种生活用品的销售单价每提高1元，其销售量相应减少4件，那么将销售价定为_____元时，才能使每天所获销售利润最大．
5．加工爆米花时，爆开且不糊的粒数的百分比称为“可食用率”．在特定条件下，可食用率y与加工时间x(单位：min)满足函数表达式y＝－0.2x2＋1.5x－2，则最佳加工时间为_______min.
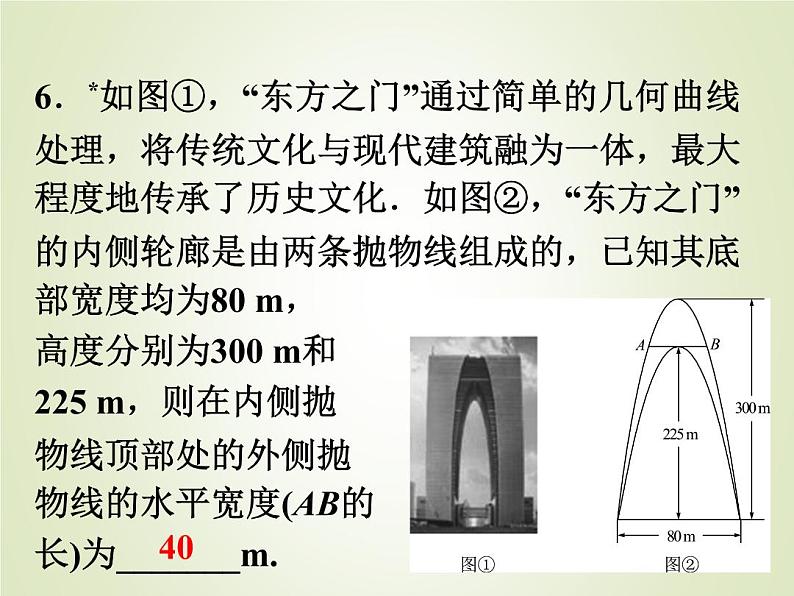
6．*如图①，“东方之门”通过简单的几何曲线处理，将传统文化与现代建筑融为一体，最大程度地传承了历史文化．如图②，“东方之门”的内侧轮廊是由两条抛物线组成的，已知其底部宽度均为80 m，高度分别为300 m和225 m，则在内侧抛物线顶部处的外侧抛物线的水平宽度(AB的长)为_______m.
7．(2021·衢州)如图①是一座抛物线型拱桥侧面示意图．水面宽AB与桥长CD均为24 m，在距离D点6米的E处，测得桥面到桥拱的距离EF为1.5 m，以桥拱顶点O为原点，桥面为x轴建立平面直角坐标系．(1)求桥拱顶部O离水面的距离；
(2)如图②，桥面上方有3根高度均为4 m的支柱CG，OH，DI，过相邻两根支柱顶端的钢缆呈形状相同的抛物线，其最低点到桥面距离为1 m.①求出其中一条钢缆抛物线的函数表达式．②为庆祝节日，在钢缆和桥拱之间竖直装饰若干条彩带，求彩带长度的最小值．
8．(2021·南充)超市购进某种苹果，如果进价增加2元/千克要用300元；如果进价减少2元/千克，同样数量的苹果只用200元．(1)求苹果的进价；(2)如果购进这种苹果不超过100千克，就按原价购进；如果购进苹果超过100千克，超过部分购进价格减少2元/千克，写出购进苹果的支出y(元)与购进数量x(千克)之间的函数关系式；
9．(2018·江西)小贤与小杰在探究某类二次函数问题时，经历了如下过程：求解体验：(1)已知抛物线y＝－x2＋bx－3经过点(－1，0)，则b＝________，顶点坐标为________，该抛物线关于点(0，1)成中心对称的抛物线表达式是______________.
抽象感悟：我们定义：对于抛物线y＝ax2＋bx＋c(a≠0)，以y轴上的点M(0，m)为中心，作该抛物线关于点M中心对称的抛物线y′，则我们又称抛物线y′为抛物线y的“衍生抛物线”，点M为“衍生中心”．(2)已知抛物线y＝－x2－2x＋5关于点(0，m)的衍生抛物线为y′，若这两条抛物线有交点，求m的取值范围．
问题解决：(3)已知抛物线y＝ax2＋2ax－b(a≠0)①若抛物线y的衍生抛物线为y′＝bx2－2bx＋a2(b≠0)，两抛物线有两个交点，且恰好是它们的顶点，求a，b的值及衍生中心的坐标；
②若抛物线y关于点(0，k＋12)的衍生抛物线为y1，其顶点为A1；关于点(0，k＋22)的衍生抛物线为y2，其顶点为A2；…；关于点(0，k＋n2)的衍生抛物线为yn，其顶点为An…(n为正整数).求AnAn＋1的长(用含n的式子表示).
解：求解体验：(1)－4，(－2，1)，y＝x2－4x＋5抽象感悟：(2)∵抛物线y＝－x2－2x＋5＝－(x＋1)2＋6①，∴抛物线的顶点坐标为(－1，6)，设衍生抛物线为y′＝a(x－1)2＋2m－6，∵抛物线y＝－x2－2x＋5关于点(0，m)的衍生抛物线为y′，∴a＝1，∴衍生抛物线为y′＝(x－1)2＋2m－6＝x2－2x＋2m－5②，联立①②得，x2－2x＋2m－5＝－x2－2x＋5，整理得，2x2＝10－2m，∵这两条抛物线有交点，∴10－2m≥0，∴m≤5；
问题解决：(3)①抛物线y＝ax2＋2ax－b＝a(x＋1)2－a－b，∴此抛物线的顶点坐标为(－1，－a－b)，∵抛物线y的衍生抛物线为y′＝bx2－2bx＋a2＝b(x－1)2＋a2－b，∴a＋b＝0，③∵两个抛物线有两个交点，且恰好是它们的顶点，∴b＋2b＋a2＝－a－b④，联立③④，∴a＝0(舍)或a＝3，∴b＝－3，∴抛物线y的顶点坐标为(－1，0)，抛物线y的衍生抛物线的顶点坐标为(1，12)，∴衍生中心的坐标为(0，6)；
②抛物线y＝ax2＋2ax－b的顶点坐标为(－1，－a－b)，∵点(－1，－a－b)关于点(0，k＋n2)的对称点为(1，a＋b＋2k＋2n2)，∴抛物线yn的顶点坐标An为(1，a＋b＋2k＋2n2)，同理：An＋1(1，a＋b＋2k＋2(n＋1)2)，∴AnAn＋1＝a＋b＋2k＋2(n＋1)2－(a＋b＋2k＋2n2)＝4n＋2.