

(新高考)高考数学一轮考点复习2.8《函数模型及其应用》学案 (含详解)
展开第八节 函数模型及其应用
核心素养立意下的命题导向
1.利用给出的具体函数模型解决实际问题,凸显数学运算的核心素养.
2.给出具体实际问题,借助所学基本初等函数的特点,建立恰当的函数模型解决实际问题,凸显数学建模、数学运算的核心素养.
[理清主干知识]
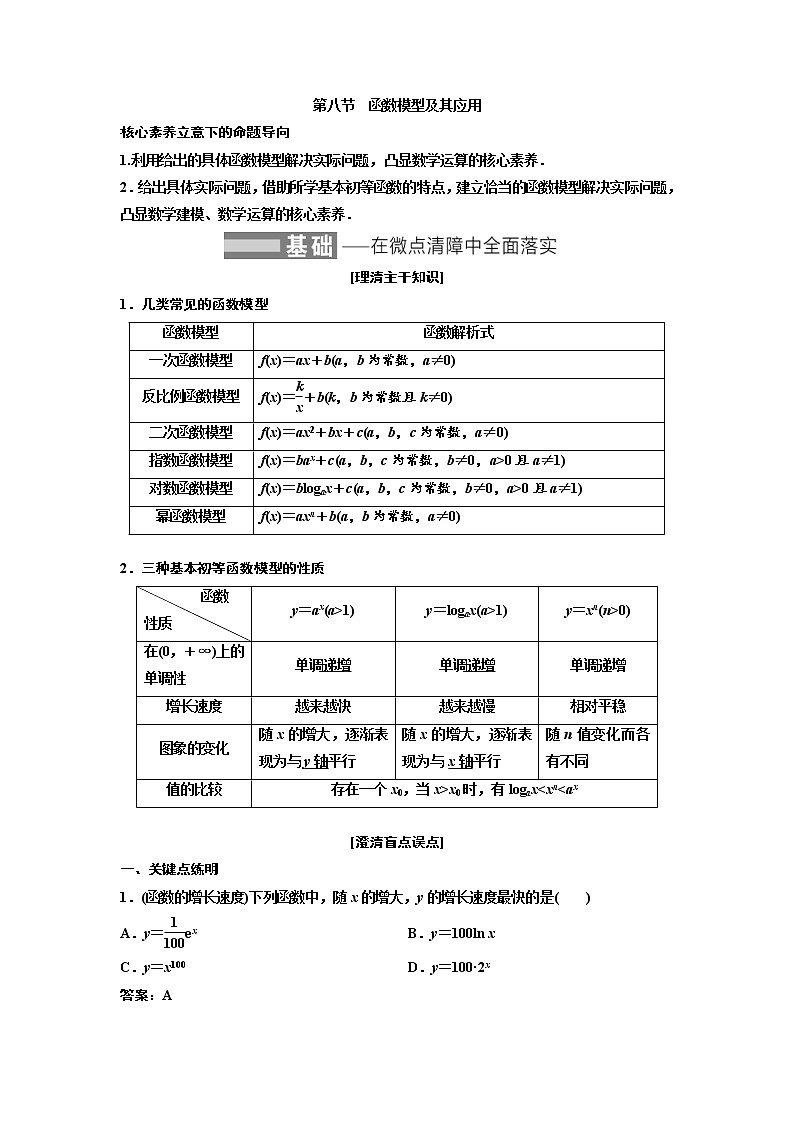
1.几类常见的函数模型
函数模型
函数解析式
一次函数模型
f(x)=ax+b(a,b为常数,a≠0)
反比例函数模型
f(x)=+b(k,b为常数且k≠0)
二次函数模型
f(x)=ax2+bx+c(a,b,c为常数,a≠0)
指数函数模型
f(x)=bax+c(a,b,c为常数,b≠0,a>0且a≠1)
对数函数模型
f(x)=blogax+c(a,b,c为常数,b≠0,a>0且a≠1)
幂函数模型
f(x)=axn+b(a,b为常数,a≠0)
2.三种基本初等函数模型的性质
函数
性质
y=ax(a>1)
y=logax(a>1)
y=xn(n>0)
在(0,+∞)上的单调性
单调递增
单调递增
单调递增
增长速度
越来越快
越来越慢
相对平稳
图象的变化
随x的增大,逐渐表现为与y轴平行
随x的增大,逐渐表现为与x轴平行
随n值变化而各有不同
值的比较
存在一个x0,当x>x0时,有logax
[澄清盲点误点]
一、关键点练明
1.(函数的增长速度)下列函数中,随x的增大,y的增长速度最快的是( )
A.y=ex B.y=100ln x
C.y=x100 D.y=100·2x
答案:A
2.(二次函数模型)某物体一天内的温度T关于时间t的函数解析式为T(t)=t3-3t+60,时间单位是h,温度单位为℃,t=0时表示中午12:00,则上午8:00时的温度为( )
A.8 ℃ B.18 ℃
C.58 ℃ D.128 ℃
答案:A
3.(对数函数模型)在不考虑空气阻力的情况下,火箭的最大速度v米/秒和燃料的质量M千克、火箭(除燃料外)的质量m千克的函数关系式是v=2 000·ln.当燃料质量是火箭质量的________倍时,火箭的最大速度可达12千米/秒.
解析:当v=12 000时,2 000·ln=12 000,
∴ln=6,∴=e6-1.
答案:e6-1
4.(分段函数模型)某城市客运公司确定客票价格的方法是:如果行程不超过100 km,票价是0.5元/km,如果超过100 km,超过100 km的部分按0.4元/km定价,则客运票价y(元)与行驶千米数x(km)之间的函数关系式是________________.
答案:y=
二、易错点练清
1.(对函数增长速度理解不深致误)在某个物理实验中,测量得变量x和变量y的几组数据,如下表:
x
0.50
0.99
2.01
3.98
y
-0.99
0.01
0.98
2.00
则对x,y最适合的拟合函数是( )
A.y=2x B.y=x2-1
C.y=2x-2 D.y=log2x
答案:D
2.(构建函数模型失误)某商店每月按出厂价每瓶3元购进一种饮料,根据以前的统计数据,若零售价定为每瓶4元,每月可销售400瓶;若零售价每降低(升高)0.5元,则可多(少)销售40瓶,在每月的进货当月销售完的前提下,为获得最大利润,销售价应定为( )
A.3.75元/瓶 B.7.5元/瓶
C.12元/瓶 D.6元/瓶
解析:选D 设销售价每瓶定为x元,利润为y元,则y=(x-3)=80(x-3)(9-x)=-80(x-6)2+720(x≥3),所以x=6时,y取得最大值.
3.(计算失误)某公司为了业务发展制定了一个激励销售人员的奖励方案,在销售额x为8万元时,奖励1万元;销售额x为64万元时,奖励4万元.若公司拟定的奖励模型为y=alog4x+b.某业务员要得到8万元奖励,则他的销售额应为________万元.
解析:依题意得即解得a=2,b=-2,所以y=2log4x-2.
当y=8时,2log4x-2=8,解得x=1 024.
答案:1 024
考点一 应用所给函数模型解决实际问题
[典例] (2020·全国卷Ⅲ)Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:I(t)=,其中K为最大确诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3)( )
A.60 B.63
C.66 D.69
[解析] 由题意可知,当I(t*)=0.95K时,=0.95K,
即=1+e-0.23(t*-53),e-0.23(t*-53)=,e0.23(t*-53)=19,∴0.23(t*-53)=ln 19≈3,∴t*≈66.故选C.
[答案] C
[方法技巧]
应用所给函数模型解决实际问题的3个关注点
(1)认清所给函数模型,弄清哪些量为待定系数.
(2)根据已知利用待定系数法,确定模型中的待定系数.
(3)利用该模型求解实际问题.
[针对训练]
一个容器装有细沙a cm3,细沙从容器底部一个细微的小孔慢慢地匀速漏出,t min后剩余的细沙量为y=ae-bt(cm3),经过8 min后发现容器内还有一半的沙子,则再经过______min,容器中的沙子只有开始时的八分之一.
解析:当t=0时,y=a,当t=8时,y=ae-8b=a,
∴e-8b=.令y=a,即ae-bt=a,e-bt==(e-8b)3=e-24b,则t=24,∴再经过16 min,容器中的沙子只有开始时的八分之一.
答案:16
考点二 构建函数模型解决实际问题
考法(一) 构建二次函数模型
[例1] (2021·武汉检测)如图,已知边长为8米的正方形钢板有一个角被锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,在五边形ABCDE内截取一个矩形BNPM,使点P在边DE上.
(1)设MP=x米,PN=y米,将y表示成x的函数,并求该函数的解析式及定义域;
(2)求矩形BNPM面积的最大值.
[解] (1)如图,作PQ⊥AF于Q,所以PQ=8-y,EQ=x-4,
在△EDF中,=,
所以=,所以y=-x+10,定义域为{x|4≤x≤8}.
(2)设矩形BNPM的面积为S,
则S(x)=xy=x(10-)=-(x-10)2+50,
所以S(x)是关于x的二次函数,且其图象开口向下,对称轴为直线x=10,
所以当x∈[4,8]时,S(x)单调递增,
所以当x=8时,矩形BNPM的面积取得最大值,最大值为48平方米.
[方法技巧]
在建立二次函数模型解决实际问题中的最优问题时,一定要注意自变量的取值范围,需根据函数图象的对称轴与函数定义域在坐标系中对应区间之间的位置关系讨论求解.解决函数应用问题时,最后还要还原到实际问题.
考法(二) 构建指数函数、对数函数模型
[例2] (1)当生物死亡后,其体内原有的碳14的含量大约每经过5 730年衰减为原来的一半,这个时间称为“半衰期”.当死亡生物体内的碳14含量不足死亡前的千分之一时,用一般的放射性探测器就测不到了.若某死亡生物体内的碳14用该放射性探测器探测不到,则它经过的“半衰期”个数至少是( )
A.8 B.9
C.10 D.11
(2)已知世界人口在过去40年翻了一番,则每年人口平均增长率约是(参考数据: lg 2≈0.301 0,100.007 5≈1.017)( )
A.1.5% B.1.6%
C.1.7% D.1.8%
[解析] (1)设该死亡生物体内原有的碳14的含量为1,则经过n个“半衰期”后的含量为n,由n<,得n≥10,所以,若某死亡生物体内的碳14用该放射性探测器探测不到,则它至少需要经过10个“半衰期”.故选C.
(2)设每年人口平均增长率为x,则(1+x)40=2,两边取以10为底的对数,则40lg(1+x)=lg 2,所以lg(1+x)=≈0.007 5,所以100.007 5=1+x,得1+x≈1.017,所以x≈1.7%.故选C.
[答案] (1)C (2)C
[方法技巧]
两类函数模型的应用技巧
(1)与指数函数、对数函数两类函数模型有关的实际问题,在求解时,要先学会合理选择模型,在两类模型中,指数函数模型是增长速度越来越快(底数大于1)的一类函数模型,与增长率、银行利率有关的问题都属于指数函数模型.
(2)在解决指数函数、对数函数模型问题时,一般需要先通过待定系数法确定函数解析式,再借助函数的图象求解最值问题,必要时可借助导数.
考法(三) 构建y=x+(a>0)型函数模型
[例3] 某校为丰富师生课余活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S(平方米)的AMPN矩形健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上.已知∠ACB=60°,|AC|=30米,|AM|=x米,x∈[10,20].设矩形AMPN健身场地每平方米的造价为元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为元(k为正常数).
(1)试用x表示S,并求S的取值范围;
(2)求总造价T关于面积S的函数T=f(S);
(3)如何选取|AM|,使总造价T最低(不要求求出最低造价)?
[解] (1)在Rt△PMC中,显然|MC|=30-x,∠PCM=60°,|PM|=|MC|·tan∠PCM= (30-x),
∴矩形AMPN的面积S=|PM|·|AM|=x(30-x),x∈[10,20],
由x(30-x)≤2=225,
可知当x=15时,S取得最大值为225,
当x=10或20时,S取得最小值为200,
∴S的取值范围为[200,225].
(2)矩形AMPN健身场地造价T1=37k,
又∵△ABC的面积为450,
∴草坪造价T2=(450-S).
∴总造价f(S)=T=T1+T2=25k,200≤S≤225.
(3)∵+≥12,
当且仅当=,即S=216时等号成立,
此时x(30-x)=216,解得x=12或x=18.
故选取|AM|为12米或18米时总造价T最低.
[方法技巧]
“y=x+(a>0)”型函数模型的求解策略
(1)“y=x+”型函数模型在实际问题中会经常出现.解决此类问题,关键是利用已知条件,建立函数模型,然后化简整理函数解析式,必要时通过配凑得到“y=x+”型函数模型.
(2)求函数解析式时要先确定函数的定义域.对于y=x+(a>0,x>0)类型的函数最值问题,要特别注意定义域和基本不等式中等号成立的条件,如果在定义域内满足等号成立,可考虑用基本不等式求最值,否则要考虑函数的单调性,此时可借用导数来研究函数的单调性.
考法(四) 构建分段函数模型
[例4] 国庆期间,某旅行社组团去风景区旅游,若每团人数在30或30以下,飞机票每张收费900元;若每团人数多于30,则给予优惠:每多1人,机票每张减少10元,直到达到规定人数75为止.每团乘飞机,旅行社需付给航空公司包机费15 000元.
(1)写出飞机票的价格关于人数的函数;
(2)每团人数为多少时,旅行社可获得最大利润?
[解] (1)设每团人数为x,由题意得0
即y=
(2)设旅行社获利S元,
则S=
即S=
因为S=900x-15 000在区间(0,30]上为增函数,
故当x=30时,S取最大值12 000.
又S=-10(x-60)2+21 000,x∈(30,75],所以当x=60时,S取得最大值21 000.
综上,当x=60时,旅行社可获得最大利润.
[方法技巧]
分段函数模型的求解策略
(1)实际问题中有些变量间的关系不能用同一个关系式给出,而是由几个不同的关系式构成,如出租车票价与路程之间的关系,应构建分段函数模型求解.
(2)构建分段函数时,要力求准确、简捷,做到分段合理、不重不漏.
(3)分段函数的最值是各段最大值(或最小值)中的最大者(或最小者).
[针对训练]
1.某商场销售A型商品.已知该商品的进价是每件3元,且销售单价与日均销售量的关系如下表所示:
销售单价/元
4
5
6
7
8
9
10
日均销售量/件
400
360
320
280
240
200
160
请根据以上数据分析,要使该商品的日均销售利润最大,则此商品的定价(单位:元/件)应为( )
A.4 B.5.5
C.8.5 D.10
解析: 选C 设定价为x元/件时,日均销售利润为y元,则y=(x-3)·[400-(x-4)·40]=-402+1 210,故当x==8.5时,该商品的日均销售利润最大,故选C.
2.在标准温度和大气压下,人体血液中氢离子的物质的量的浓度(单位mol/L,记作 [H+])和氢氧根离子的物质的量的浓度(单位mol/L,记作[OH-])的乘积等于常数10-14.已知pH值的定义为pH=-lg[H+],健康人体血液的pH值保持在7.35~7.45之间,那么健康人体血液中的可以为(参考数据:lg 2=0.30,lg 3=0.48)( )
A. B.
C. D.
解析:选C ∵[H+]·[OH-]=10-14,∴=1014·[H+]2,∵7.35<-lg[H+]<7.45, ∴10-7.45<[H+]<10-7.35,∴10-0.9<=1014·[H+]2<10-0.7,又10-0.9=>,lg(100.7)=0.7>lg 3,∴100.7>3,10-0.7<,∴<<.
3.已知某服装厂生产某种品牌的衣服,销售量q(x)(单位:百件)关于每件衣服的利润x(单位:元)的函数解析式为q(x)=当每件衣服的利润为多少元时,该服装厂所获效益最大?并求出最大值.
解:设该服装厂所获效益为f(x)元,
则f(x)=100xq(x)=
当0
当20
当80≤x≤180时,f′(x)≤0,f(x)单调递减,
所以当x=80时,f(x)有极大值,也是最大值240 000.
综上,当每件衣服的利润为80元时,该服装厂所获效益最大,且最大值为240 000元.
1.有一组实验数据如下表所示:
t
1
2
3
4
5
s
1.5
5.9
13.4
24.1
37
下列所给函数模型较适合的是( )
A.y=logax(a>1) B.y=ax+b(a>1)
C.y=ax2+b(a>0) D.y=logax+b(a>1)
解析:选C 由题表中数据可知,s随t的增大而增大且增长速度越来越快,A、D中的函数的增长速度越来越慢,B中的函数的增长速度保持不变,C中的函数在x>1时,y随x的增大而增大,且增长速度越来越快.故选C.
2.某新产品投放市场后第一个月销售100台,第二个月销售200台,第三个月销售400台,第四个月销售790台,则下列函数模型中能较好地反映销量y与投放市场的月数x之间关系的是( )
A.y=100x B.y=50x2-50x+100
C.y=50×2x D.y=100log2x+100
解析:选C 根据函数模型的增长差异和题目中的数据可知,应为指数函数模型.故选C.
3.某市生产总值连续两年持续增加.第一年的增长率为p,第二年的增长率为q,则该市这两年生产总值的年平均增长率为( )
A. B.
C. D.-1
解析:选D 设年平均增长率为x,原生产总值为a,则a(1+p)·(1+q)=a(1+x)2,解得x=-1,故选D.
4.(多选)某工厂生产一种溶液,按市场要求该溶液的杂质含量不得超过0.1%,而这种溶液最初的杂质含量为2%,现进行过滤,已知每过滤一次杂质含量减少,若使这种溶液的杂质含量达到市场要求,则过滤次数可以为(参考数据:lg 2≈0.301,lg 3≈0.477)( )
A.6 B.7
C.8 D.9
解析:选CD 设经过n次过滤这种溶液的含量达到市场要求,则×n≤,即n≤,
两边取对数得nlg≤-lg 20,
即n(lg 2-lg 3)≤-(1+lg 2),
得n≥≈7.4,故选C、D.
5.(2020·新高考全国卷Ⅰ)基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:I(t)=ert描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0=1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln 2≈0.69)( )
A.1.2天 B.1.8天
C.2.5天 D.3.5天
解析:选B ∵R0=1+rT,∴3.28=1+6r,∴r=0.38.
由题意,累计感染病例数增加1倍,
则I(t2)=2I(t1),即e0.38t2=2e0.38t1,
∴e0.38(t2-t1)=2,即0.38(t2-t1)=ln 2≈0.69,
解得t2-t1≈1.8,故选B.
6.(2021·安徽淮北月考)华罗庚是上世纪我国伟大的数学家,以华氏命名的数学科研成果有“华氏定理”“华氏不等式”“华王方法”等.他除了数学理论研究,还在生产一线大力推广了“优选法”和“统筹法”.“优选法”,是指研究如何用较少的试验次数,迅速找到最优方案的一种科学方法.在当前防疫取得重要进展的时刻,为防范机场带来的境外输入,某机场海关在对入境人员进行检测时采用了“优选法”提高检测效率:每16人为一组,把每个人抽取的鼻咽拭子分泌物混合检查,若为阴性,则全部放行;若为阳性,则对该16人再次抽检确认感染者.某组16人中恰有一人感染(鼻咽拭子样本检验将会是阳性),若逐一检测可能需要15次才能确认感染者.现在先把这16人均分为2组,选其中一组8人的样本混合检查,若为阴性,则认定在另一组;若为阳性,则认定在本组.继续把认定的这组的8人均分为2组,选其中一组4人的样本混合检查……依此类推,最终从这16人中认定那名感染者需要经过检测的次数为( )
A.3 B.4
C.6 D.7
解析:选B 先把这16人均分为2组,选其中一组8人的样本混合检查,若为阴性,则认定在另一组;若为阳性,则认定在本组,此时进行了1次检测.继续把认定的这组的8人均分为2组,选其中一组4人的样本混合检查,若为阴性,则认定在另一组;若为阳性,则认定在本组,此时进行了2次检测.继续把认定的这组的4人均分为2组,选其中一组2人的样本混合检查,若为阴性,则认定在另一组;若为阳性,则认定在本组,此时进行了3次检测.选认定的这组的2人中一人进行样本检查,若为阴性,则认定是另一个人;若为阳性,则认定为此人,此时进行了4次检测.所以,最终从这16人中认定那名感染者需要经过4次检测.故选B.
7.如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4 m和a m(0
解析:选B 设AD长为x,则CD长为16-x.
又因为要将P点围在矩形ABCD内,所以a≤x≤12.
则矩形ABCD的面积为x(16-x).
当0
8.某单位为鼓励职工节约用水,作出如下规定:每位职工每月用水不超过10立方米的,按每立方米3元收费;用水超过10立方米的,超过的部分按每立方米5元收费.某职工某月的水费为55元,则该职工这个月实际用水为( )
A.13立方米 B.14立方米
C.15立方米 D.16立方米
解析:选C 设该职工某月的实际用水为x立方米时,水费为y元,由题意得y=即y=易知该职工这个月的实际用水量超过10立方米,所以5x-20=55,解得x=15,故选C.
9.某地区要建造一条防洪堤,其横断面为等腰梯形ABCD,腰与底边夹角为60°(如图),考虑防洪堤坚固性及石块用料等因素,设计其横断面面积为9平方米,且高度不低于米.记防洪堤横断面的腰长为x米,外周长(梯形的上底线段BC与两腰长的和)为y米.要使防洪堤横断面的外周长不超过10.5米,则其腰长x的取值范围为( )
A.[2,4] B.[3,4]
C.[2,5] D.[3,5]
解析:选B 根据题意知,9=(AD+BC)h,其中AD=BC+2×=BC+x,h= x,所以9=(2BC+x)x,得BC=-,由得2≤x<6.所以y=BC+2x=+(2≤x<6),由y=+≤10.5,解得3≤x≤4.因为[3,4]⊆[2,6),所以腰长x的取值范围为[3,4].故选B.
10.成都市某物流公司为了配合“北改”项目顺利进行,决定把三环内的租用仓库搬迁到北三环外重新租地建设.已知仓库每月占用费y1与仓库到车站的距离成反比,而每月车载货物的运费y2与仓库到车站的距离成正比.据测算,如果在距离车站10千米处建仓库,这两项费用y1,y2分别是2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站( )
A.5千米处 B.4千米处
C.3千米处 D.2千米处
解析:选A 设仓库应建在离车站x千米处.因为仓库每月占用费y1与仓库到车站的距离成反比,所以令反比例系数为m(m>0),则y1=.当x=10时,y1==2,所以m=20.因为每月车载货物的运费y2与仓库到车站的距离成正比,所以令正比例系数为n(n>0),则y2=nx,当x=10时,y2=10n=8,所以n=.所以两项费用之和为y=y1+y2=+≥ 2 =8,当且仅当=,即x=5时取等号.所以要使这两项费用之和最小,仓库应建在离车站5千米处.故选A.
11.中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年文明史得到国际社会认可,良渚古城遗址是人类早期城市文明的范例,实证了中华五千年文明史,考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳14的质量N随时间t(单位:年)的衰变规律满足N=N0·2(N0表示碳14原有的质量),则经过5 730年后,碳14的质量变为原来的________;经过测定,良渚古城遗址文物样本中碳14的质量是原来的至,据此推测良渚古城存在的时期距今约在5 730年到________年之间.(参考数据:lg 2≈0.30,lg 7≈0.85,lg 3≈0.48)
解析:∵N=N0·2,∴当t=5 730时,N=N0·2-1=N0.∴经过5 730年后,碳14的质量变为原来的.
由题意可知2>,
两边同时取以2为底的对数得,log22>log2,
∴>=≈-1.2,∴t<6 876,
∴推测良渚古城存在的时期距今约在5 730年到6 876年之间.
答案: 6 876
12.已知某品牌商品靠广告宣传得到的收入R与广告费A之间满足关系R=a(a为常数且a>0),广告效应D=a-A.那么对于此商品,精明的商人为了取得最大的广告效应,投入的广告费应为________.(用常数a表示)
解析:由题意得D=a-A=-2+,且A≥0,∴当=,即A=时,D最大,最大为.
答案:
13.某工厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量P(毫克/升)与时间t(小时)的关系为P=P0e-kt,P0为过滤前的污染物数量.如果在前5小时消除了10%的污染物,那么污染物减少19%需要花费的时间为________小时.
解析:由题设可得(1-0.1)P0=P0e-5k,即0.9=e-5k,故-5k=ln 0.9;又(1-0.19)P0=P0e-kt,即0.81=e-kt,故-kt=ln 0.81=2ln 0.9=-10k,故t=10.
答案:10
14.某人准备购置一块占地1 800平方米的矩形地块,中间建三个矩形温室大棚,大棚周围均是宽为1米的小路(如阴影部分所示),大棚占地面积为S平方米,其中a∶b=1∶2,若要使S最大,则y=________.
解析:由题意可得xy=1 800,b=2a,则y=a+b+3=3a+3,S=(x-2)a+(x-3)×b=(3x-8)a=(3x-8)×=1 808-3x-y=1 808-3x-×=1 808-≤1 808-2 =1 808-240=1 568,当且仅当3x=,即x=40时取等号,所以当S取得最大值时,y==45.
答案:45
15.“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度v(单位:千克/年)是养殖密度x(单位:尾/立方米)的函数.当x不超过4尾/立方米时,v的值为2千克/年;当4
解:(1)由题意得当0
由已知得解得
所以v=-x+,故函数v=
(2)设年生长量为f(x)千克/立方米,依题意并由(1)可得,f(x)=
当0
即当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值为12.5千克/立方米.
16.某厂有一个容量300吨的水塔,每天从早六点到晚十点供应生活和生产用水,已知该厂生活用水每小时10吨,生产用水总量W(吨)与时间t(单位:小时,规定早晨六点时t=0)的函数关系为W=100,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级,进水量增加10吨.若某天水塔原有水100吨,在供应时同时打开进水管,问该天进水量应选择第几级,既能保证该厂用水(即水塔中水不空),又不会使水溢出?
解:设水塔进水量选择第n级,在t时刻水塔中的水容量y等于水塔中的存水量100吨加上进水量10nt吨,减去生活用水10t吨,再减去生产用水W=100吨,
即y=100+10nt-10t-100(0
++1=202-≥,
所以
(1)若建立函数模型y=f(x)制定奖励方案,请你根据题意,写出奖励函数模型应满足的条件;
(2)现有两个奖励函数模型:(ⅰ)y=x+1;(ⅱ)y=log2x-2.试分析这两个函数模型是否符合公司要求.
解:(1)设奖励函数模型为y=f(x),
则该函数模型满足的条件是:
①当x∈[10,100]时,f(x)是增函数;
②当x∈[10,100]时,f(x)≤5恒成立;
③当x∈[10,100]时,f(x)≤恒成立.
(2)对于函数模型(ⅰ)y=x+1,
它在[10,100]上是增函数,满足条件①;
但当x=80时,y=5,因此,当x>80时,y>5,不满足条件②,故该函数模型不符合公司要求.
对于函数模型(ⅱ)y=log2x-2,它在[10,100]上是增函数,满足条件①;
x=100时,ymax=log2100-2=2log25<5,即f(x)≤5恒成立.满足条件②;
设h(x)=log2x-2-x,则h′(x)=-,
又x∈[10,100],所以≤≤,
所以h′(x)≤-<-=0,
所以h(x)在[10,100]上是递减的,因此h(x)≤h(10)=log210-4<0,即f(x)≤恒成立,满足条件③.
故该函数模型符合公司要求.
综上所述,函数模型(ⅱ)y=log2x-2符合公司要求.
(新高考)高考数学一轮复习学案3.9《函数模型及其应用》(含详解): 这是一份(新高考)高考数学一轮复习学案3.9《函数模型及其应用》(含详解),共16页。学案主要包含了知识梳理,教材衍化等内容,欢迎下载使用。
(新高考)高考数学一轮考点复习1.1《集合》学案 (含详解): 这是一份(新高考)高考数学一轮考点复习1.1《集合》学案 (含详解),共13页。
(新高考)高考数学一轮考点复习8.4《椭圆》学案 (含详解): 这是一份(新高考)高考数学一轮考点复习8.4《椭圆》学案 (含详解),共24页。












