辽宁省大连市2021-2022学年中考数学最后冲刺浓缩精华卷含解析

这是一份辽宁省大连市2021-2022学年中考数学最后冲刺浓缩精华卷含解析，共21页。试卷主要包含了答题时请按要求用笔，方程的解是等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项:
1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。
2．答题时请按要求用笔。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（共10小题，每小题3分，共30分）
1．下列计算中，正确的是（　　）
A．a•3a=4a2 B．2a+3a=5a2
C．（ab）3=a3b3 D．7a3÷14a2=2a
2．某市2017年实现生产总值达280亿的目标，用科学记数法表示“280亿”为（　　）
A．28×109 B．2.8×108 C．2.8×109 D．2.8×1010
3．如图，在菱形ABCD中，AB=BD，点E，F分别在AB，AD上，且AE=DF,连接BF与DE相交于点G，连接CG与BD相交于点H,下列结论：
①△AED≌△DFB；②S四边形 BCDG=CG2；③若AF=2DF，则BG=6GF
,其中正确的结论

A．只有①②. B．只有①③. C．只有②③. D．①②③.
4．如图，三角形纸片ABC，AB＝10cm，BC＝7cm，AC＝6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为（　　）

A．9cm B．13cm C．16cm D．10cm
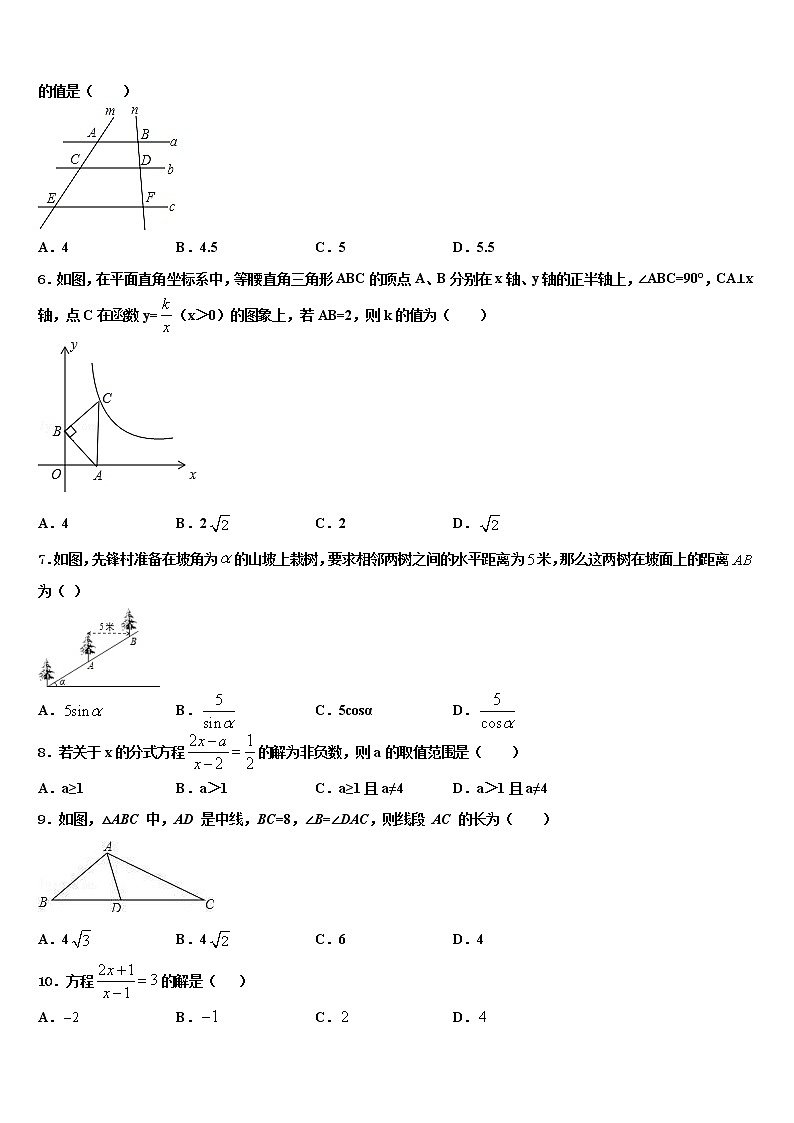
5．如图，已知直线a∥b∥c，直线m，n与a，b，c分别交于点A，C，E，B，D，F，若AC=4，CE=6，BD=3，则DF的值是（　　）

A．4 B．4.5 C．5 D．5.5
6．如图，在平面直角坐标系中，等腰直角三角形ABC的顶点A、B分别在x轴、y轴的正半轴上，∠ABC=90°，CA⊥x轴，点C在函数y=（x＞0）的图象上，若AB=2，则k的值为（　　）

A．4 B．2 C．2 D．
7．如图，先锋村准备在坡角为的山坡上栽树，要求相邻两树之间的水平距离为米，那么这两树在坡面上的距离为（ ）

A． B． C．5cosα D．
8．若关于x的分式方程的解为非负数，则a的取值范围是（　　）
A．a≥1 B．a＞1 C．a≥1且a≠4 D．a＞1且a≠4
9．如图，△ABC 中，AD 是中线，BC=8，∠B=∠DAC，则线段 AC 的长为（ ）

A．4 B．4 C．6 D．4
10．方程的解是（ ）
A． B． C． D．
二、填空题（本大题共6个小题，每小题3分，共18分）
11．如图，中，，则 __________．

12． 如图，已知,要使,还需添加一个条件，则可以添加的条件是 ．（只写一个即可，不需要添加辅助线）

13．某市政府为了改善城市容貌，绿化环境，计划经过两年时间，使绿地面积增加44%，则这两年平均绿地面积的增长率为______.
14．化简:＝ __________.
15．的相反数是_____，倒数是_____，绝对值是_____
16．为了了解某班数学成绩情况，抽样调查了13份试卷成绩，结果如下：3个140分，4个135分，2个130分，2个120分，1个100分，1个80分．则这组数据的中位数为______分．
三、解答题（共8题，共72分）
17．（8分）已知关于的二次函数
（1）当时，求该函数图像的顶点坐标.
（2）在（1）条件下，为该函数图像上的一点，若关于原点的对称点也落在该函数图像上，求的值
（3）当函数的图像经过点（1，0）时，若是该函数图像上的两点，试比较与的大小.
18．（8分）我们把两条中线互相垂直的三角形称为“中垂三角形”．例如图1，图2，图1中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均为“中垂三角形”．设BC＝a，AC＝b，AB＝c．
特例探索
（1）如图1，当∠ABE＝45°，c＝时，a＝ ，b＝ ；
如图2，当∠ABE＝10°，c＝4时，a＝ ，b＝ ；

归纳证明
（2）请你观察（1）中的计算结果，猜想a2，b2，c2三者之间的关系，用等式表示出来，请利用图1证明你发现的关系式；
拓展应用
（1）如图4，在□ABCD中，点E，F，G分别是AD，BC，CD的中点，BE⊥EG，AD＝，AB＝1．求AF的长．

19．（8分）先化简，然后从﹣＜x＜的范围内选取一个合适的整数作为x的值代入求值．
20．（8分）如图，已知抛物线y=x2+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．
（1）求抛物线的解析式；
（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；
（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．

21．（8分）如图，已知△ABC是等边三角形，点D在AC边上一点，连接BD，以BD为边在AB的左侧作等边△DEB，连接AE，求证：AB平分∠EAC．

22．（10分）如图，在△ABC中，AB＝AC，以AB为直径作半圆⊙O，交BC于点D，连接AD．过点D作DE⊥AC，垂足为点E．求证：DE是⊙O的切线；当⊙O半径为3，CE＝2时，求BD长．

23．（12分）如图，在五边形ABCDE中，∠BCD=∠EDC=90°，BC=ED，AC=AD．求证：△ABC≌△AED；当∠B=140°时，求∠BAE的度数．

24．某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动，每位同学必须且只能选择一项球类运动，对该校学生随机抽取进行调查，根据调查结果绘制了如下不完整的频数分布表和扇形统计图：
运动项目

频数(人数)

羽毛球

30

篮球



乒乓球

36

排球



足球

12


请根据以上图表信息解答下列问题：频数分布表中的 ， ；在扇形统计图中，“排球”所在的扇形的圆心角为 度；全校有多少名学生选择参加乒乓球运动？



参考答案

一、选择题（共10小题，每小题3分，共30分）
1、C
【解析】
根据同底数幂的运算法则进行判断即可.
【详解】
解：A、a•3a=3a2，故原选项计算错误；
B、2a+3a=5a，故原选项计算错误；
C、（ab）3=a3b3，故原选项计算正确；
D、7a3÷14a2=a，故原选项计算错误；
故选C．
【点睛】
本题考点：同底数幂的混合运算.
2、D
【解析】
根据科学计数法的定义来表示数字，选出正确答案.
【详解】
解：把一个数表示成a（1≤a<10，n为整数）与10的幂相乘的形式，这种记数法叫做科学记数法，280亿用科学计数法表示为2.8×1010，所以答案选D.
【点睛】
本题考查学生对科学计数法的概念的掌握和将数字用科学计数法表示的能力.
3、D
【解析】
解：①∵ABCD为菱形，∴AB=AD．

∵AB=BD，∴△ABD为等边三角形．
∴∠A=∠BDF=60°．
又∵AE=DF，AD=BD，
∴△AED≌△DFB；
②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD，
即∠BGD+∠BCD=180°，
∴点B、C、D、G四点共圆，
∴∠BGC=∠BDC=60°，∠DGC=∠DBC=60°．
∴∠BGC=∠DGC=60°．
过点C作CM⊥GB于M，CN⊥GD于N．
∴CM=CN，
则△CBM≌△CDN，（HL）
∴S四边形BCDG=S四边形CMGN．
S四边形CMGN=1S△CMG，
∵∠CGM=60°，
∴GM=CG，CM=CG，
∴S四边形CMGN=1S△CMG=1××CG×CG=CG1．

③过点F作FP∥AE于P点．
∵AF=1FD，
∴FP：AE=DF：DA=1：3，
∵AE=DF，AB=AD，
∴BE=1AE，
∴FP：BE=1：6=FG：BG，
即 BG=6GF．
故选D．
4、A
【解析】
试题分析：由折叠的性质知，CD=DE，BC=BE．
易求AE及△AED的周长．
解：由折叠的性质知，CD=DE，BC=BE=7cm．
∵AB=10cm，BC=7cm，∴AE=AB﹣BE=3cm．
△AED的周长=AD+DE+AE=AC+AE=6+3=9（cm）．
故选A．
点评：本题利用了折叠的性质：折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
5、B
【解析】
试题分析：根据平行线分线段成比例可得，然后根据AC=1，CE=6，BD=3，可代入求解DF=1．2．
故选B
考点：平行线分线段成比例
6、A
【解析】
【分析】作BD⊥AC于D，如图，先利用等腰直角三角形的性质得到AC=AB=2，BD=AD=CD=，再利用AC⊥x轴得到C（，2），然后根据反比例函数图象上点的坐标特征计算k的值．
【详解】作BD⊥AC于D，如图，
∵△ABC为等腰直角三角形，
∴AC=AB=2，
∴BD=AD=CD=，
∵AC⊥x轴，
∴C（，2），
把C（，2）代入y=得k=×2=4，
故选A．

【点睛】本题考查了等腰直角三角形的性质以及反比例函数图象上点的坐标特征，熟知反比例函数y=（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy=k是解题的关键.
7、D
【解析】
利用所给的角的余弦值求解即可．
【详解】
∵BC=5米，∠CBA=∠α，∴AB==．
故选D．

【点睛】
本题主要考查学生对坡度、坡角的理解及运用．
8、C
【解析】
试题分析：分式方程去分母转化为整式方程，表示出整式方程的解，根据解为非负数及分式方程分母不为1求出a的范围即可．
解：去分母得：2（2x﹣a）=x﹣2，
解得：x=，
由题意得：≥1且≠2，
解得：a≥1且a≠4，
故选C．
点睛：此题考查了分式方程的解，需注意在任何时候都要考虑分母不为1．
9、B
【解析】
由已知条件可得,可得出,可求出AC的长．
【详解】
解：由题意得：∠B=∠DAC，∠ACB=∠ACD,所以，根据“相似三角形对应边成比例”，得，又AD 是中线，BC=8，得DC=4,代入可得AC=,
故选B.
【点睛】
本题主要考查相似三角形的判定与性质．灵活运用相似的性质可得出解答．
10、D
【解析】
按照解分式方程的步骤进行计算，注意结果要检验.
【详解】
解：





经检验x=4是原方程的解
故选：D
【点睛】
本题考查解分式方程，注意结果要检验.

二、填空题（本大题共6个小题，每小题3分，共18分）
11、17
【解析】
∵Rt△ABC中，∠C=90°，∴tanA= ，
∵，∴AC＝8，
∴AB= =17,
故答案为17.
12、可添∠ABD=∠CBD或AD=CD．
【解析】
由AB=BC结合图形可知这两个三角形有两组边对应相等，添加一组边利用SSS证明全等，也可以添加一对夹角相等，利用SAS证明全等，据此即可得答案.
【详解】
.可添∠ABD=∠CBD或AD=CD，
①∠ABD=∠CBD，
在△ABD和△CBD中，
∵，
∴△ABD≌△CBD（SAS）；
②AD=CD，
在△ABD和△CBD中，
∵，
∴△ABD≌△CBD（SSS），
故答案为∠ABD=∠CBD或AD=CD．
【点睛】
本题考查了三角形全等的判定，结合图形与已知条件灵活应用全等三角形的判定方法是解题的关键. 熟记全等三角形的判定方法有：SSS，SAS，ASA，AAS．
13、10%
【解析】
本题可设这两年平均每年的增长率为x，因为经过两年时间，让市区绿地面积增加44%，则有（1+x）1=1+44%，解这个方程即可求出答案．
【详解】
解：设这两年平均每年的绿地增长率为x，根据题意得，
（1+x）1=1+44%，
解得x1=-1.1（舍去），x1=0.1．
答：这两年平均每年绿地面积的增长率为10%．
故答案为10%
【点睛】
此题考查增长率的问题，一般公式为：原来的量×（1±x）1=现在的量，增长用+，减少用-．但要注意解的取舍，及每一次增长的基础．
14、a+b
【解析】
将原式通分相减，然后用平方差公式分解因式，再约分化简即可。
【详解】
解：原式=
=
=
=a+b
【点睛】
此题主要考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
15、 ,
【解析】
∵只有符号不同的两个数是互为相反数，
∴的相反数是；
∵乘积为1的两个数互为倒数，
∴的倒数是；
∵负数得绝对值是它的相反数，
∴绝对值是
故答案为(1). (2). (3).
16、1
【解析】
∵13份试卷成绩，结果如下：3个140分，4个1分，2个130分，2个120分，1个100分，1个80分，
∴第7个数是1分，
∴中位数为1分，
故答案为1．

三、解答题（共8题，共72分）
17、（1） ，顶点坐标（1，-4）；（2）m=1；（3）①当a＞0时，y2＞y1 ，②当a＜0时，y1＞y2 .
【解析】
试题分析：
（1）把a=2，b=4代入并配方，即可求出此时二次函数图象的顶点坐标；
（2）由题意把（m，t）和（-m，-t）代入（1）中所得函数的解析式，解方程组即可求得m的值；
（3）把点（1，0）代入可得b=a-2，由此可得抛物线的对称轴为直线：，再分a>0和a<0两种情况分别讨论即可y1和y2的大小关系了.
试题解析：
（1）把a=2，b=4代入得：，
∴此时二次函数的图象的顶点坐标为（1，-4）；
（2）由题意，把（m，t）和（-m，-t）代入得：
①，②，
由①+②得：，解得：；
（3）把点（1，0）代入得a-b-2=0，
∴b=a-2，
∴此时该二次函数图象的对称轴为直线：，
①当a>0时，，，
∵此时，且抛物线开口向上，
∴中，点B距离对称轴更远，
∴y1 ②当a<0时，，，
∵此时，且抛物线开口向下，
∴中，点B距离对称轴更远，
∴y1>y2；
综上所述，当a>0时，y1y2.
点睛：在抛物线上：（1）当抛物线开口向上时，抛物线上的点到对称轴的距离越远，所对应的函数值就越大；（2）当抛物线开口向下时，抛物线上的点到对称轴的距离越近，所对应的函数值就越大；
18、（1）2，2；2，2；（2）+=5；（1）AF=2．
【解析】
试题分析：（1）∵AF⊥BE，∠ABE=25°，∴AP=BP=AB=2，∵AF，BE是△ABC的中线，∴EF∥AB，EF=AB=，∴∠PFE=∠PEF=25°，∴PE=PF=1，在Rt△FPB和Rt△PEA中，AE=BF==，∴AC=BC=2，∴a=b=2，如图2，连接EF，同理可得：EF=×2=2，∵EF∥AB，∴△PEF～△ABP，∴，在Rt△ABP中，AB=2，∠ABP=10°，∴AP=2，PB=2，∴PF=1，PE=，在Rt△APE和Rt△BPF中，AE=，BF=，∴a=2，b=2，故答案为2，2，2，2；
（2）猜想：a2+b2=5c2，如图1，连接EF，设∠ABP=α，∴AP=csinα，PB=ccosα，由（1）同理可得，PF=PA=，PE==，AE2=AP2+PE2=c2sin2α+，BF2=PB2+PF2=+c2cos2α，∴=c2sin2α+，=+c2cos2α，∴+=+c2cos2α+c2sin2α+，∴a2+b2=5c2；
（1）如图2，连接AC，EF交于H，AC与BE交于点Q，设BE与AF的交点为P，∵点E、G分别是AD，CD的中点，∴EG∥AC，∵BE⊥EG，∴BE⊥AC，∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC=2，∴∠EAH=∠FCH，∵E，F分别是AD，BC的中点，∴AE=AD，BF=BC，∴AE=BF=CF=AD=，∵AE∥BF，∴四边形ABFE是平行四边形，∴EF=AB=1，AP=PF，在△AEH和△CFH中，，∴△AEH≌△CFH，∴EH=FH，∴EQ，AH分别是△AFE的中线，由（2）的结论得：AF2+EF2=5AE2，∴AF2=5﹣EF2=16，∴AF=2．

考点：相似形综合题．
19、
【解析】
根据分式的减法和除法可以化简题目中的式子，然后从﹣＜x＜的范围内选取一个使得原分式有意义的整数作为x的值代入即可解答本题．
【详解】
解：÷（﹣x+1）
=
=
=
=，
当x=﹣2时，原式= ．
【点睛】
本题考查分式的化简求值、估算无理数的大小，解答本题的关键是明确分式化简求值的方法．
20、 (1) 抛物线的解析式为y=x2-2x+1，(2) 四边形AECP的面积的最大值是，点P（，﹣）；(3) Q（4,1）或（-3，1）.
【解析】
(1)把点A，B的坐标代入抛物线的解析式中，求b，c；(2)设P(m，m2−2m＋1)，根据S四边形AECP＝S△AEC＋S△APC，把S四边形AECP用含m式子表示，根据二次函数的性质求解；(3)设Q(t，1)，分别求出点A，B，C，P的坐标，求出AB，BC，CA；用含t的式子表示出PQ，CQ，判断出∠BAC＝∠PCA＝45°，则要分两种情况讨论，根据相似三角形的对应边成比例求t.
【详解】
解：(1)将A(0，1)，B(9，10)代入函数解析式得：
×81＋9b＋c＝10，c＝1，解得b＝−2，c＝1，
所以抛物线的解析式y＝x2−2x＋1；
(2)∵AC∥x轴，A(0，1)，
∴x2−2x＋1＝1，解得x1＝6，x2＝0(舍)，即C点坐标为(6，1)，
∵点A(0，1)，点B(9，10)，
∴直线AB的解析式为y＝x＋1，设P(m，m2−2m＋1)，∴E(m，m＋1)，
∴PE＝m＋1−(m2−2m＋1)＝−m2＋3m.
∵AC⊥PE，AC＝6，
∴S四边形AECP＝S△AEC＋S△APC＝AC⋅EF＋AC⋅PF
＝AC⋅(EF＋PF)＝AC⋅EP
＝×6(−m2＋3m)＝−m2＋9m.
∵0 ∴当m＝时，四边形AECP的面积最大值是，此时P()；
(3)∵y＝x2−2x＋1＝(x−3)2−2，
P(3，−2)，PF＝yF−yp＝3，CF＝xF−xC＝3，
∴PF＝CF，∴∠PCF＝45∘，
同理可得∠EAF＝45∘，∴∠PCF＝∠EAF，
∴在直线AC上存在满足条件的点Q，
设Q(t，1)且AB＝，AC＝6，CP＝，
∵以C，P，Q为顶点的三角形与△ABC相似，
①当△CPQ∽△ABC时，
CQ:AC＝CP:AB，(6−t):6＝，解得t＝4，所以Q(4，1)；
②当△CQP∽△ABC时，
CQ:AB＝CP:AC，(6−t)6，解得t＝−3，所以Q(−3，1).
综上所述：当点P为抛物线的顶点时，在直线AC上存在点Q，使得以C，P，Q为顶点的三角形与△ABC相似，Q点的坐标为(4，1)或(−3，1).

【点睛】
本题考查了二次函数综合题，解（1）的关键是待定系数法；解（2）的关键是利用面积的和差得出二次函数，又利用了二次函数的性质，平行于坐标轴的直线上两点间的距离是较大的坐标减较小的坐标；解（3）的关键是利用相似三角形的性质的出关于CQ的比例，要分类讨论，以防遗漏．
21、详见解析
【解析】
由等边三角形的性质得出AB=BC，BD=BE，∠BAC=∠BCA=∠ABC=∠DBE=60°，证出∠ABE=∠CBD，证明△ABE≌△CBD（SAS），得出∠BAE=∠BCD=60°，得出∠BAE=∠BAC，即可得出结论．
【详解】
证明：∵△ABC，△DEB都是等边三角形，
∴AB＝BC，BD＝BE，∠BAC＝∠BCA＝∠ABC＝∠DBE＝60°，
∴∠ABC﹣∠ABD＝∠DBE﹣∠ABD，
即∠ABE＝∠CBD，
在△ABE和△CBD中，
∵AB=CB,
∠ABE=∠CBD,
BE=BD,，
∴△ABE≌△CBD（SAS），
∴∠BAE＝∠BCD＝60°，
∴∠BAE＝∠BAC，
∴AB平分∠EAC．
【点睛】
本题考查了全等三角形的判定与性质，等边三角形的性质等知识，熟练掌握等边三角形的性质，证明三角形全等是解题的关键．
22、（1）证明见解析；（2）BD＝2．
【解析】
（1）连接OD，AB为⊙0的直径得∠ADB=90°，由AB=AC，根据等腰三角形性质得AD平分BC，即DB=DC，则OD为△ABC的中位线，所以OD∥AC，而DE⊥AC，则OD⊥DE，然后根据切线的判定方法即可得到结论；
（2）由∠B=∠C，∠CED=∠BDA=90°，得出△DEC∽△ADB，得出，从而求得BD•CD=AB•CE，由BD=CD，即可求得BD2=AB•CE，然后代入数据即可得到结果．
【详解】
（1）证明：连接OD，如图，

∵AB为⊙0的直径，
∴∠ADB＝90°，
∴AD⊥BC，
∵AB＝AC，
∴AD平分BC，即DB＝DC，
∵OA＝OB，
∴OD为△ABC的中位线，
∴OD∥AC，
∵DE⊥AC，
∴OD⊥DE，
∴DE是⊙0的切线；
（2）∵∠B＝∠C，∠CED＝∠BDA＝90°，
∴△DEC∽△ADB，
∴，
∴BD•CD＝AB•CE，
∵BD＝CD，
∴BD2＝AB•CE，
∵⊙O半径为3，CE＝2，
∴BD＝＝2．
【点睛】
本题考查了切线的判定定理：过半径的外端点且与半径垂直的直线为圆的切线．也考查了等腰三角形的性质、三角形相似的判定和性质．
23、（1）详见解析；（2）80°．
【分析】（1）根据∠ACD=∠ADC，∠BCD=∠EDC=90°，可得∠ACB=∠ADE，进而运用SAS即可判定全等三角形；
（2）根据全等三角形对应角相等，运用五边形内角和，即可得到∠BAE的度数．
【解析】
（1）根据∠ACD=∠ADC，∠BCD=∠EDC=90°，可得∠ACB=∠ADE，进而运用SAS即可判定全等三角形；
（2）根据全等三角形对应角相等，运用五边形内角和，即可得到∠BAE的度数．
【详解】
证明：（1）∵AC=AD，
∴∠ACD=∠ADC，
又∵∠BCD=∠EDC=90°，
∴∠ACB=∠ADE，
在△ABC和△AED中，
，
∴△ABC≌△AED（SAS）；
解：（2）当∠B=140°时，∠E=140°，
又∵∠BCD=∠EDC=90°，
∴五边形ABCDE中，∠BAE=540°﹣140°×2﹣90°×2=80°．
【点睛】
考点：全等三角形的判定与性质．
24、 (1)24，1；(2) 54；（3）360.
【解析】
（1）根据选择乒乓球运动的人数是36人，对应的百分比是30%，即可求得总人数，然后利用百分比的定义求得a，用总人数减去其它组的人数求得b；
（2）利用360°乘以对应的百分比即可求得；
（3）求得全校总人数，然后利用总人数乘以对应的百分比求解．
【详解】
（1）抽取的人数是36÷30%＝120（人），
则a＝120×20%＝24，
b＝120﹣30﹣24﹣36﹣12＝1．
故答案是：24，1；
（2）“排球”所在的扇形的圆心角为360°×＝54°，
故答案是：54；
（3）全校总人数是120÷10%＝1200（人），
则选择参加乒乓球运动的人数是1200×30%＝360（人）．