

江西省德安县塘山中学2021-2022学年中考试题猜想数学试卷含解析
展开2021-2022中考数学模拟试卷
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)
1.如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )
A.13 B.17 C.18 D.25
2.根据如图所示的程序计算函数y的值,若输入的x值是4或7时,输出的y值相等,则b等于( )
A.9 B.7 C.﹣9 D.﹣7
3.函数y=中自变量x的取值范围是
A.x≥0 B.x≥4 C.x≤4 D.x>4
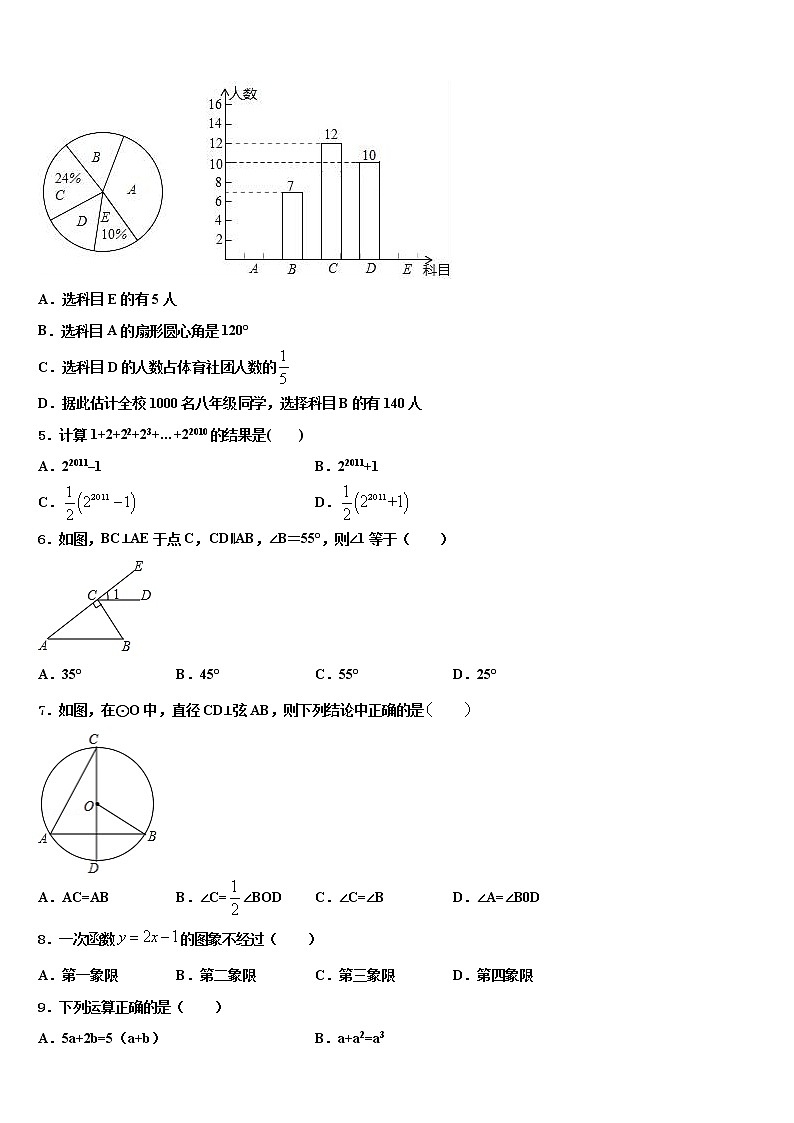
4.为丰富学生课外活动,某校积极开展社团活动,开设的体育社团有:A:篮球,B:排球,C:足球,D:羽毛球,E:乒乓球.学生可根据自己的爱好选择一项,李老师对八年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )
A.选科目E的有5人
B.选科目A的扇形圆心角是120°
C.选科目D的人数占体育社团人数的
D.据此估计全校1000名八年级同学,选择科目B的有140人
5.计算1+2+22+23+…+22010的结果是( )
A.22011–1 B.22011+1
C. D.
6.如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
A.35° B.45° C.55° D.25°
7.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是
A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠B0D
8.一次函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.下列运算正确的是( )
A.5a+2b=5(a+b) B.a+a2=a3
C.2a3•3a2=6a5 D.(a3)2=a5
10.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )
A.90°-α B.90°+ α C. D.360°-α
二、填空题(共7小题,每小题3分,满分21分)
11.可燃冰是一种新型能源,它的密度很小,可燃冰的质量仅为.数字0.00092用科学记数法表示是__________.
12.如图,矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为______.
13.如果a是不为1的有理数,我们把称为a的差倒数如:2的差倒数是,-1的差倒数是,已知,是的差倒数,是的差倒数,是的差倒数,…,依此类推,则 ___________ .
14.如图,一次函数y1=kx+b的图象与反比例函数y2=(x<0)的图象相交于点A和点B.当y1>y2>0时,x的取值范围是_____.
15.如图,点G是的重心,AG的延长线交BC于点D,过点G作交AC于点E,如果,那么线段GE的长为______.
16.如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数的图象经过点C,则k的值为 .
17.要使分式有意义,则x的取值范围为_________.
三、解答题(共7小题,满分69分)
18.(10分)如图,在平面直角坐标系中,一次函数的图象分别交x轴、y轴于A、B两点,与反比例函数的图象交于C、D两点.已知点C的坐标是(6,-1),D(n,3).求m的值和点D的坐标.求的值.根据图象直接写出:当x为何值时,一次函数的值大于反比例函数的值?
19.(5分)网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
20.(8分)已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.求证:AP=BQ;在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.
21.(10分)如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(-3,m+8),B(n,-6)两点.求一次函数与反比例函数的解析式;求△AOB的面积.
22.(10分)“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 度;请补全条形统计图;若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
23.(12分)计算:2﹣1+|﹣|++2cos30°
24.(14分)如图,△ABC中,∠A=90°,AB=AC=4,D是BC边上一点,将点D绕点A逆时针旋转60°得到点E,连接CE.
(1)当点E在BC边上时,画出图形并求出∠BAD的度数;
(2)当△CDE为等腰三角形时,求∠BAD的度数;
(3)在点D的运动过程中,求CE的最小值.
(参考数值:sin75°=, cos75°=,tan75°=)
参考答案
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)
1、C
【解析】
在Rt△ABC中,∠ACB=90°,BC=12,AC=5,根据勾股定理求得AB=13.根据题意可知,EF为线段AB的垂直平分线,在Rt△ABC中,根据直角三角形斜边的中线等于斜边的一半可得CD=AD=AB,所以△ACD的周长为AC+CD+AD=AC+AB=5+13=18.故选C.
2、C
【解析】
先求出x=7时y的值,再将x=4、y=-1代入y=2x+b可得答案.
【详解】
∵当x=7时,y=6-7=-1,
∴当x=4时,y=2×4+b=-1,
解得:b=-9,
故选C.
【点睛】
本题主要考查函数值,解题的关键是掌握函数值的计算方法.
3、B
【解析】
根据二次根式的性质,被开方数大于等于0,列不等式求解.
【详解】
根据题意得:x﹣1≥0,解得x≥1,
则自变量x的取值范围是x≥1.
故选B.
【点睛】
本题主要考查函数自变量的取值范围的知识点,注意:二次根式的被开方数是非负数.
4、B
【解析】
A选项先求出调查的学生人数,再求选科目E的人数来判定,
B选项先求出A科目人数,再利用×360°判定即可,
C选项中由D的人数及总人数即可判定,
D选项利用总人数乘以样本中B人数所占比例即可判定.
【详解】
解:调查的学生人数为:12÷24%=50(人),选科目E的人数为:50×10%=5(人),故A选项正确,
选科目A的人数为50﹣(7+12+10+5)=16人,选科目A的扇形圆心角是×360°=115.2°,故B选项错误,
选科目D的人数为10,总人数为50人,所以选科目D的人数占体育社团人数的,故C选项正确,
估计全校1000名八年级同学,选择科目B的有1000×=140人,故D选项正确;
故选B.
【点睛】
本题主要考查了条形统计图及扇形统计图,解题的关键是读懂统计图,从统计图中找到准确信息.
5、A
【解析】
可设其和为S,则2S=2+22+23+24+…+22010+22011,两式相减可得答案.
【详解】
设S=1+2+22+23+…+22010①
则2S=2+22+23+…+22010+22011②
②-①得S=22011-1.
故选A.
【点睛】
本题考查了因式分解的应用;设出和为S,并求出2S进行做差求解是解题关键.
6、A
【解析】
根据垂直的定义得到∠∠BCE=90°,根据平行线的性质求出∠BCD=55°,计算即可.
【详解】
解:∵BC⊥AE,
∴∠BCE=90°,
∵CD∥AB,∠B=55°,
∴∠BCD=∠B=55°,
∴∠1=90°-55°=35°,
故选:A.
【点睛】
本题考查的是平行线的性质和垂直的定义,两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.
7、B
【解析】
先利用垂径定理得到弧AD=弧BD,然后根据圆周角定理得到∠C=∠BOD,从而可对各选项进行判断.
【详解】
解:∵直径CD⊥弦AB,
∴弧AD =弧BD,
∴∠C=∠BOD.
故选B.
【点睛】
本题考查了垂径定理和圆周角定理,垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
8、B
【解析】
由二次函数,可得函数图像经过一、三、四象限,所以不经过第二象限
【详解】
解:∵,
∴函数图象一定经过一、三象限;
又∵,函数与y轴交于y轴负半轴,
∴函数经过一、三、四象限,不经过第二象限
故选B
【点睛】
此题考查一次函数的性质,要熟记一次函数的k、b对函数图象位置的影响
9、C
【解析】
直接利用合并同类项法则以及单项式乘以单项式、幂的乘方运算法则分别化简得出答案.
【详解】
A、5a+2b,无法计算,故此选项错误;
B、a+a2,无法计算,故此选项错误;
C、2a3•3a2=6a5,故此选项正确;
D、(a3)2=a6,故此选项错误.
故选C.
【点睛】
此题主要考查了合并同类项以及单项式乘以单项式、幂的乘方运算,正确掌握运算法则是解题关键.
10、C
【解析】
试题分析:∵四边形ABCD中,∠ABC+∠BCD=360°﹣(∠A+∠D)=360°﹣α,
∵PB和PC分别为∠ABC、∠BCD的平分线,
∴∠PBC+∠PCB=(∠ABC+∠BCD)=(360°﹣α)=180°﹣α,
则∠P=180°﹣(∠PBC+∠PCB)=180°﹣(180°﹣α)=α.
故选C.
考点:1.多边形内角与外角2.三角形内角和定理.
二、填空题(共7小题,每小题3分,满分21分)
11、9.2×10﹣1.
【解析】
根据科学记数法的正确表示为,由题意可得0.00092用科学记数法表示是9.2×10﹣1.
【详解】
根据科学记数法的正确表示形式可得:
0.00092用科学记数法表示是9.2×10﹣1.
故答案为: 9.2×10﹣1.
【点睛】
本题主要考查科学记数法的正确表现形式,解决本题的关键是要熟练掌握科学记数法的正确表现形式.
12、1.5或3
【解析】
根据矩形的性质,利用勾股定理求得AC==5,由题意,可分△EFC是直角三角形的两种情况:
如图1,当∠EFC=90°时,由∠AFE=∠B=90°,∠EFC=90°,可知点F在对角线AC上,且AE是∠BAC的平分线,所以可得BE=EF,然后再根据相似三角形的判定与性质,可知△ABC∽△EFC,即,代入数据可得,解得BE=1.5;
如图2,当∠FEC=90°,可知四边形ABEF是正方形,从而求出BE=AB=3.
故答案为1.5或3.
点睛:此题主要考查了翻折变换的性质,勾股定理,矩形的性质,正方形的判定与性质,利用勾股定理列方程求解是常用的方法,本题难点在于分类讨论,做出图形更形象直观.
13、.
【解析】
利用规定的运算方法,分别算得a1,a2,a3,a4…找出运算结果的循环规律,利用规律解决问题.
【详解】
∵a1=4
a2=,
a3=,
a4=,
…
数列以4,−三个数依次不断循环,
∵2019÷3=673,
∴a2019=a3=,
故答案为:.
【点睛】
此题考查规律型:数字的变化类,倒数,解题关键在于掌握运算法则找到规律.
14、-2
根据图象可直接得到y1>y2>0时x的取值范围.
【详解】
根据图象得:当y1>y2>0时,x的取值范围是﹣2<x<﹣0.5,
故答案为﹣2<x<﹣0.5.
【点睛】
本题考查了反比例函数与一次函数的交点问题,熟悉待定系数法以及理解函数图象与不等式的关系是解题的关键.
15、2
【解析】
分析:由点G是△ABC重心,BC=6,易得CD=3,AG:AD=2:3,又由GE∥BC,可证得△AEG∽△ACD,然后由相似三角形的对应边成比例,即可求得线段GE的长.
详解:∵点G是△ABC重心,BC=6,
∴CD=BC=3,AG:AD=2:3,
∵GE∥BC,
∴△AEG∽△ADC,
∴GE:CD=AG:AD=2:3,
∴GE=2.
故答案为2.
点睛:本题考查了三角形重心的定义和性质、相似三角形的判定和性质.利用三角形重心的性质得出AG:AD=2:3是解题的关键.
16、-6
【解析】
分析:∵菱形的两条对角线的长分别是6和4,
∴A(﹣3,2).
∵点A在反比例函数的图象上,
∴,解得k=-6.
【详解】
请在此输入详解!
17、x≠1
【解析】
由题意得
x-1≠0,
∴x≠1.
故答案为x≠1.
三、解答题(共7小题,满分69分)
18、(1)m=-6,点D的坐标为(-2,3);(2);(3)当或时,一次函数的值大于反比例函数的值.
【解析】
(1)将点C的坐标(6,-1)代入即可求出m,再把D(n,3)代入反比例函数解析式求出n即可.
(2)根据C(6,-1)、D(-2,3)得出直线CD的解析式,再求出直线CD与x轴和y轴的交点即可,得出OA、OB的长,再根据锐角三角函数的定义即可求得;
(3)根据函数的图象和交点坐标即可求得.
【详解】
⑴把C(6,-1)代入,得.
则反比例函数的解析式为,
把代入,得,
∴点D的坐标为(-2,3).
⑵将C(6,-1)、D(-2,3)代入,得
,解得.
∴一次函数的解析式为,
∴点B的坐标为(0,2),点A的坐标为(4,0).
∴,
在在中,
∴.
⑶根据函数图象可知,当或时,一次函数的值大于反比例函数的值
【点睛】
此题考查了反比例函数与一次函数的交点问题.其知识点有解直角三角形,待定系数法求解析式,此题难度适中,注意掌握数形结合思想与方程思想的应用.
19、 (1)1500;(2)见解析;(3)108°;(3)12~23岁的人数为400万
【解析】
试题分析:(1)根据30-35岁的人数和所占的百分比求调查的人数;
(2)从调查的总人数中减去已知的三组的人数,即可得到12-17岁的人数,据此补全条形统计图;
(3)先计算18-23岁的人数占调查总人数的百分比,再计算这一组所对应的圆心角的度数;
(4)先计算调查中12﹣23岁的人数所占的百分比,再求网瘾人数约为2000万中的12﹣23岁的人数.
试题解析:解:(1)结合条形统计图和扇形统计图可知,30-35岁的人数为330人,所占的百分比为22%,所以调查的总人数为330÷22%=1500人.
故答案为1500 ;
(2)1500-450-420-330=300人.
补全的条形统计图如图:
(3)18-23岁这一组所对应的圆心角的度数为360×=108°.
故答案为108° ;
(4)(300+450)÷1500=50%,.
考点:条形统计图;扇形统计图.
20、(1)证明见解析;(2)①AQ﹣AP=PQ,②AQ﹣BQ=PQ,③DP﹣AP=PQ,④DP﹣BQ=PQ.
【解析】
试题分析:(1)利用AAS证明△AQB≌△DPA,可得AP=BQ;(2)根据AQ﹣AP=PQ和全等三角形的对应边相等可写出4对线段.
试题解析:(1)在正方形中ABCD中,AD=BA,∠BAD=90°,∴∠BAQ+∠DAP=90°,∵DP⊥AQ,∴∠ADP+∠DAP=90°,∴∠BAQ=∠ADP,∵AQ⊥BE于点Q,DP⊥AQ于点P,∴∠AQB=∠DPA=90°,∴△AQB≌△DPA(AAS),
∴AP=BQ.(2)①AQ﹣AP=PQ,②AQ﹣BQ=PQ,③DP﹣AP=PQ,④DP﹣BQ=PQ.
考点:(1)正方形;(2)全等三角形的判定与性质.
21、(1)y=-,y=-2x-1(2)1
【解析】
试题分析:(1)将点A坐标代入反比例函数求出m的值,从而得到点A的坐标以及反比例函数解析式,再将点B坐标代入反比例函数求出n的值,从而得到点B的坐标,然后利用待定系数法求一次函数解析式求解;
(2)设AB与x轴相交于点C,根据一次函数解析式求出点C的坐标,从而得到点OC的长度,再根据S△AOB=S△AOC+S△BOC列式计算即可得解.
试题解析:(1)将A(﹣3,m+8)代入反比例函数y=得,
=m+8,
解得m=﹣6,
m+8=﹣6+8=2,
所以,点A的坐标为(﹣3,2),
反比例函数解析式为y=﹣,
将点B(n,﹣6)代入y=﹣得,﹣=﹣6,
解得n=1,
所以,点B的坐标为(1,﹣6),
将点A(﹣3,2),B(1,﹣6)代入y=kx+b得,
,
解得,
所以,一次函数解析式为y=﹣2x﹣1;
(2)设AB与x轴相交于点C,
令﹣2x﹣1=0解得x=﹣2,
所以,点C的坐标为(﹣2,0),
所以,OC=2,
S△AOB=S△AOC+S△BOC,
=×2×3+×2×1,
=3+1,
=1.
考点:反比例函数与一次函数的交点问题.
22、 (1) 60,90;(2)见解析;(3) 300人
【解析】
(1)由了解很少的有30人,占50%,可求得接受问卷调查的学生数,继而求得扇形统计图中“基本了解”部分所对应扇形的圆心角;
(2)由(1)可求得了解的人数,继而补全条形统计图;
(3)利用样本估计总体的方法,即可求得答案.
【详解】
解:(1)∵了解很少的有30人,占50%,
∴接受问卷调查的学生共有:30÷50%=60(人);
∴扇形统计图中“基本了解”部分所对应扇形的圆心角为:×360°=90°;
故答案为60,90;
(2)60﹣15﹣30﹣10=5;
补全条形统计图得:
(3)根据题意得:900×=300(人),
则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为300人.
【点睛】
本题考查了条形统计图与扇形统计图,解题的关键是熟练的掌握条形统计图与扇形统计图的相关知识点.
23、+4.
【解析】
原式利用负整数指数幂法则,二次根式性质,以及特殊角的三角函数值计算即可求出值.
【详解】
原式=++2+2×=+4.
【点睛】
本题考查了实数的运算,涉及了负整数指数幂、特殊角的三角函数值、二次根式的化简等,熟练掌握各运算的运算法则是解本题的关键.
24、(1)∠BAD=15°;(2)∠BAC=45°或∠BAD =60°;(3)CE=.
【解析】
(1)如图1中,当点E在BC上时.只要证明△BAD≌△CAE,即可推出∠BAD=∠CAE=(90°-60°)=15°;
(2)分两种情形求解①如图2中,当BD=DC时,易知AD=CD=DE,此时△DEC是等腰三角形.②如图3中,当CD=CE时,△DEC是等腰三角形;
(3)如图4中,当E在BC上时,E记为E′,D记为D′,连接EE′.作CM⊥EE′于M,E′N⊥AC于N,DE交AE′于O.首先确定点E的运动轨迹是直线EE′(过点E与BC成60°角的直线上),可得EC的最小值即为线段CM的长(垂线段最短).
【详解】
解:(1)如图1中,当点E在BC上时.
∵AD=AE,∠DAE=60°,
∴△ADE是等边三角形,
∴∠ADE=∠AED=60°,
∴∠ADB=∠AEC=120°,
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
在△ABD和△ACE中,
∠B=∠C,∠ADB=∠AEC,AB=AC,
∴△BAD≌△CAE,
∴∠BAD=∠CAE=(90°-60°)=15°.
(2)①如图2中,当BD=DC时,易知AD=CD=DE,此时△DEC是等腰三角形,∠BAD=∠BAC=45°.
②如图3中,当CD=CE时,△DEC是等腰三角形.
∵AD=AE,
∴AC垂直平分线段DE,
∴∠ACD=∠ACE=45°,
∴∠DCE=90°,
∴∠EDC=∠CED=45°,
∵∠B=45°,
∴∠EDC=∠B,
∴DE∥AB,
∴∠BAD=∠ADE=60°.
(3)如图4中,当E在BC上时,E记为E′,D记为D′,连接EE′.作CM⊥EE′于M,E′N⊥AC于N,DE交AE′于O.
∵∠AOE=∠DOE′,∠AE′D=∠AEO,
∴△AOE∽△DOE′,
∴AO:OD=EO:OE',
∴AO:EO=OD:OE',
∵∠AOD=∠EOE′,
∴△AOD∽△EOE′,
∴∠EE′O=∠ADO=60°,
∴点E的运动轨迹是直线EE′(过点E与BC成60°角的直线上),
∴EC的最小值即为线段CM的长(垂线段最短),
设E′N=CN=a,则AN=4-a,
在Rt△ANE′中,tan75°=AN:NE',
∴2+=,
∴a=2-,
∴CE′=CN=2-.
在Rt△CE′M中,CM=CE′•cos30°=,
∴CE的最小值为.
【点睛】
本题考查几何变换综合题、等腰直角三角形的性质、等边三角形的性质、全等三角形的判定和性质、相似三角形的判定和性质、轨迹等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,学会利用垂线段最短解决最值问题,属于中考压轴题.
2023-2024学年江西省德安县塘山中学数学九上期末综合测试模拟试题含答案: 这是一份2023-2024学年江西省德安县塘山中学数学九上期末综合测试模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,如图,在中,,,于点,在中,,,若,则的长为等内容,欢迎下载使用。
重庆市中学2021-2022学年中考试题猜想数学试卷含解析: 这是一份重庆市中学2021-2022学年中考试题猜想数学试卷含解析,共20页。
江西省赣州市大余县2021-2022学年中考试题猜想数学试卷含解析: 这是一份江西省赣州市大余县2021-2022学年中考试题猜想数学试卷含解析,共24页。试卷主要包含了平面直角坐标系中的点P等内容,欢迎下载使用。












