江苏省射阳县第二中学2021-2022学年中考数学最后冲刺模拟试卷含解析

这是一份江苏省射阳县第二中学2021-2022学年中考数学最后冲刺模拟试卷含解析，共20页。试卷主要包含了下列命题是真命题的个数有等内容，欢迎下载使用。

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题（共10小题，每小题3分，共30分）
1．下列计算错误的是（ ）
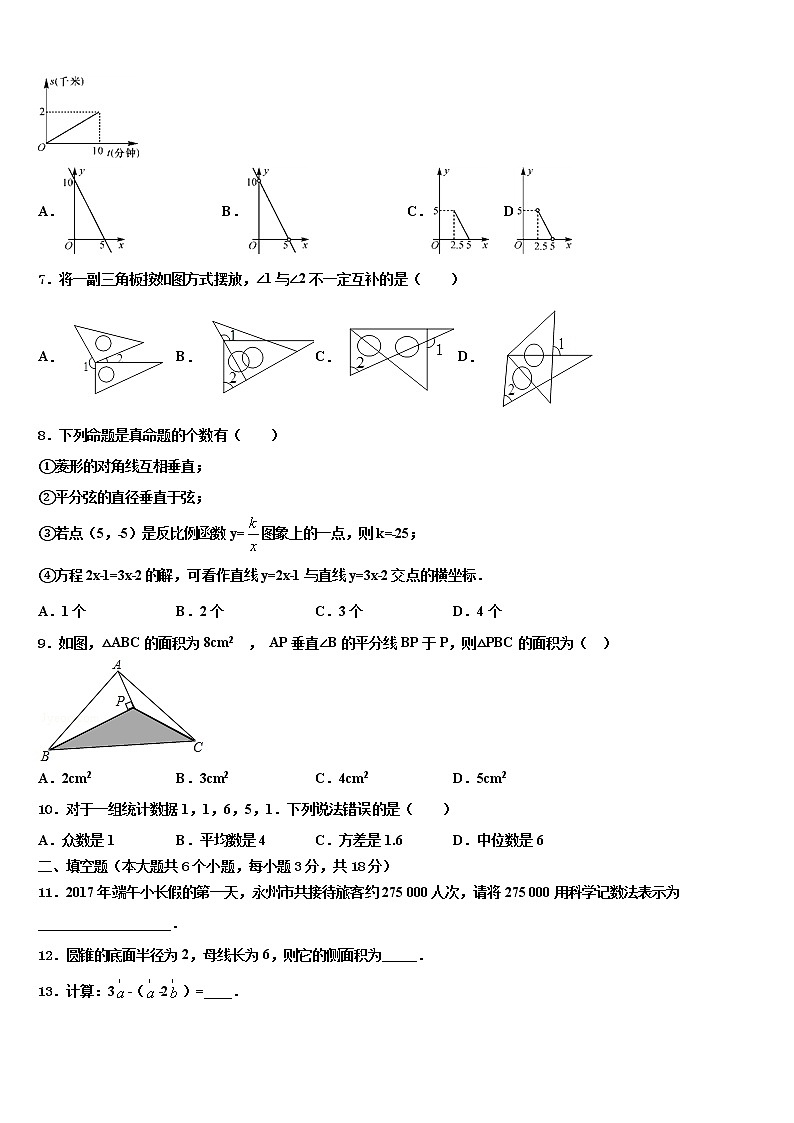
A．4x3•2x2=8x5 B．a4﹣a3=a
C．（﹣x2）5=﹣x10 D．（a﹣b）2=a2﹣2ab+b2
2．如图图形中，既是轴对称图形，又是中心对称图形的是（ ）
A．B．C．D．
3．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（ ）
A．30°B．25°
C．20°D．15°
4．港珠澳大桥是连接香港、珠海、澳门的超大型跨海通道，全长约55000米，把55000用科学记数法表示为( )
A．55×103B．5.5×104C．5.5×105D．0.55×105
5．如图，已知AC是⊙O的直径，点B在圆周上（不与A、C重合），点D在AC的延长线上，连接BD交⊙O于点E，若∠AOB=3∠ADB，则（ ）
A．DE=EBB．DE=EBC．DE=DOD．DE=OB
6．已知等腰三角形的周长是10，底边长y是腰长x的函数，则下列图象中，能正确反映y与x之间函数关系的图象是( )
A．B．C． D
7．将一副三角板按如图方式摆放，∠1与∠2不一定互补的是（ ）
A．B．C．D．
8．下列命题是真命题的个数有（ ）
①菱形的对角线互相垂直；
②平分弦的直径垂直于弦；
③若点（5，﹣5）是反比例函数y=图象上的一点，则k=﹣25；
④方程2x﹣1=3x﹣2的解，可看作直线y=2x﹣1与直线y=3x﹣2交点的横坐标．
A．1个B．2个C．3个D．4个
9．如图，△ABC的面积为8cm2 ， AP垂直∠B的平分线BP于P，则△PBC的面积为（ ）
A．2cm2 B．3cm2 C．4cm2 D．5cm2
10．对于一组统计数据1，1，6，5，1．下列说法错误的是（ ）
A．众数是1B．平均数是4C．方差是1.6D．中位数是6
二、填空题（本大题共6个小题，每小题3分，共18分）
11．2017年端午小长假的第一天，永州市共接待旅客约275 000人次，请将275 000用科学记数法表示为___________________．
12．圆锥的底面半径为2，母线长为6，则它的侧面积为_____．
13．计算：3﹣（﹣2）=____．
14．如果，那么的结果是______.
15．如图，四边形ABCD是菱形，∠BAD＝60°，AB＝6，对角线AC与BD相交于点O，点E在AC上，若OE＝2，则CE的长为_______
16．我国倡导的“一带一路”建设将促进我国与世界各国的互利合作，“一带一路”地区覆盖总人口约为4400000000人，将数据4400000000用科学记数法表示为______．
三、解答题（共8题，共72分）
17．（8分）随着高铁的建设，春运期间动车组发送旅客量越来越大，相关部门为了进一步了解春运期间动车组发送旅客量的变化情况，针对2014年至2018年春运期间的铁路发送旅客量情况进行了调查，过程如下．
（Ⅰ）收集、整理数据
请将表格补充完整：
（Ⅱ）描述数据
为了更直观地显示动车组发送旅客量占比的变化趋势，需要用什么图（回答“折线图”或“扇形图”）进行描述；
（Ⅲ）分析数据、做出推测
预估2019年春运期间动车组发送旅客量占比约为多少，说明你的预估理由．
18．（8分）如图，在△ABC中，BC＝12，tanA＝，∠B＝30°；求AC和AB的长．
19．（8分）直角三角形ABC中，，D是斜边BC上一点，且，过点C作，交AD的延长线于点E，交AB延长线于点F．
求证：；
若，，过点B作于点G，连接依题意补全图形，并求四边形ABGD的面积．
20．（8分）如图，有四张背面相同的卡片A、B、C、D，卡片的正面分别印有正三角形、平行四边形、圆、正五边形（这些卡片除图案不同外，其余均相同）．把这四张卡片背面向上洗匀后，进行下列操作：
（1）若任意抽取其中一张卡片，抽到的卡片既是中心对称图形又是轴对称图形的概率是 ；
（2）若任意抽出一张不放回，然后再从余下的抽出一张．请用树状图或列表表示摸出的两张卡片所有可能的结果，求抽出的两张卡片的图形是中心对称图形的概率．
21．（8分）（1）观察猜想
如图①点B、A、C在同一条直线上，DB⊥BC，EC⊥BC且∠DAE=90°，AD=AE，则BC、BD、CE之间的数量关系为______；
（2）问题解决
如图②，在Rt△ABC中，∠ABC=90°，CB=4，AB=2，以AC为直角边向外作等腰Rt△DAC，连结BD，求BD的长；
（3）拓展延伸
如图③，在四边形ABCD中，∠ABC=∠ADC=90°，CB=4，AB=2，DC=DA，请直接写出BD的长．
22．（10分）程大位是珠算发明家，他的名著《直指算法统宗》详述了传统的珠算规则，确立了算盘用书中有如下问题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁．意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，大、小和尚各有多少人？
23．（12分）如图，二次函数的图象与x轴交于A、B两点，与y轴交于点C，已知点A（﹣4，0）．求抛物线与直线AC的函数解析式；若点D（m，n）是抛物线在第二象限的部分上的一动点，四边形OCDA的面积为S，求S关于m的函数关系式；若点E为抛物线上任意一点，点F为x轴上任意一点，当以A、C、E、F为顶点的四边形是平行四边形时，请求出满足条件的所有点E的坐标．
24．如图，在▱ABCD中，∠BAC=90°，对角线AC，BD相交于点P，以AB为直径的⊙O分别交BC，BD于点E，Q，连接EP并延长交AD于点F．
（1）求证：EF是⊙O的切线；
（2）求证：=4BP•QP．
参考答案
一、选择题（共10小题，每小题3分，共30分）
1、B
【解析】
根据单项式与单项式相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式；合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变；幂的乘方法则：底数不变，指数相乘；完全平方公式：（a±b）1=a1±1ab+b1．可巧记为：“首平方，末平方，首末两倍中间放”可得答案．
【详解】
A选项：4x3•1x1=8x5，故原题计算正确；
B选项：a4和a3不是同类项，不能合并，故原题计算错误；
C选项：（-x1）5=-x10，故原题计算正确；
D选项：（a-b）1=a1-1ab+b1，故原题计算正确；
故选：B．
【点睛】
考查了整式的乘法，关键是掌握整式的乘法各计算法则．
2、B
【解析】
根据轴对称图形与中心对称图形的概念求解.
【详解】
解：A、是轴对称图形，不是中心对称图形，故A不正确；
B、既是轴对称图形，又是中心对称图形，故B正确；
C、是轴对称图形，不是中心对称图形，故C不正确；
D、既不是轴对称图形，也不是中心对称图形，故D不正确.
故选B.
【点睛】
本题考查了轴对称图形和中心对称图形的概念，以及对轴对称图形和中心对称图形的认识.
3、B
【解析】
根据题意可知∠1+∠2+45°=90°，∴∠2=90°﹣∠1﹣45°=25°，
4、B
【解析】
科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值>1时，n是正数；当原数的绝对值<1时，n是负数．
【详解】
55000是5位整数，小数点向左移动4位后所得的数即可满足科学记数法的要求，由此可知10的指数为4，
所以，55000用科学记数法表示为5.5×104，
故选B.
【点睛】
本题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．
5、D
【解析】
解：连接EO.
∴∠B=∠OEB，
∵∠OEB=∠D+∠DOE，∠AOB=3∠D，
∴∠B+∠D=3∠D，
∴∠D+∠DOE+∠D=3∠D，
∴∠DOE=∠D，
∴ED=EO=OB，
故选D.
6、D
【解析】
先根据三角形的周长公式求出函数关系式，再根据三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边求出x的取值范围，然后选择即可．
【详解】
由题意得，2x+y=10，
所以，y=-2x+10，
由三角形的三边关系得，，
解不等式①得，x＞2.5，
解不等式②的，x＜5，
所以，不等式组的解集是2.5＜x＜5，
正确反映y与x之间函数关系的图象是D选项图象．
故选：D．
7、D
【解析】
A选项：
∠1+∠2=360°－90°×2=180°；
B选项：
∵∠2+∠3=90°，∠3+∠4=90°，
∴∠2=∠4，
∵∠1+∠4=180°，
∴∠1+∠2=180°；
C选项：
∵∠ABC=∠DEC=90°，∴AB∥DE，∴∠2=∠EFC，
∵∠1+∠EFC=180°，∴∠1+∠2=180°；
D选项：∠1和∠2不一定互补.
故选D.
点睛：本题主要掌握平行线的性质与判定定理，关键在于通过角度之间的转化得出∠1和∠2的互补关系.
8、C
【解析】
根据菱形的性质、垂径定理、反比例函数和一次函数进行判断即可．
【详解】
解：①菱形的对角线互相垂直是真命题；
②平分弦（非直径）的直径垂直于弦，是假命题；
③若点（5，-5）是反比例函数y=图象上的一点，则k=-25，是真命题；
④方程2x-1=3x-2的解，可看作直线y=2x-1与直线y=3x-2交点的横坐标，是真命题；
故选C．
【点睛】
本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．一些命题的正确性是用推理证实的，这样的真命题叫做定理．
9、C
【解析】
延长AP交BC于E，根据AP垂直∠B的平分线BP于P，即可求出△ABP≌△BEP，又知△APC和△CPE等底同高，可以证明两三角形面积相等，即可求得△PBC的面积．
【详解】
延长AP交BC于E．
∵AP垂直∠B的平分线BP于P，∴∠ABP＝∠EBP，∠APB＝∠BPE＝90°．
在△APB和△EPB中，∵，∴△APB≌△EPB（ASA），∴S△APB＝S△EPB，AP＝PE，∴△APC和△CPE等底同高，∴S△APC＝S△PCE，∴S△PBC＝S△PBE+S△PCES△ABC＝4cm1．
故选C．
【点睛】
本题考查了三角形面积和全等三角形的性质和判定的应用，关键是求出S△PBC＝S△PBE+S△PCES△ABC．
10、D
【解析】
根据中位数、众数、方差等的概念计算即可得解.
【详解】
A、这组数据中1都出现了1次，出现的次数最多，所以这组数据的众数为1，此选项正确；
B、由平均数公式求得这组数据的平均数为4，故此选项正确；
C、S2= [（1﹣4）2+（1﹣4）2+（6﹣4）2+（5﹣4）2+（1﹣4）2]=1.6，故此选项正确；
D、将这组数据按从大到校的顺序排列，第1个数是1，故中位数为1，故此选项错误；
故选D．
考点：1.众数；2.平均数；1.方差；4.中位数.
二、填空题（本大题共6个小题，每小题3分，共18分）
11、1．75×2
【解析】
试题解析：175 000=1．75×2．
考点：科学计数法----表示较大的数
12、12π．
【解析】
试题分析：根据圆锥的底面半径为2，母线长为6，直接利用圆锥的侧面积公式求出它的侧面积．
解：根据圆锥的侧面积公式：πrl=π×2×6=12π，
故答案为12π．
考点：圆锥的计算．
13、2+2
【解析】
根据平面向量的加法法则计算即可．
【详解】
3﹣（﹣2）
=3﹣+2
=2+2，
故答案为：2+2，
【点睛】
本题考查平面向量，熟练掌握平面向量的加法法则是解题的关键．
14、1
【解析】
令k，则a=2k，b=3k，代入到原式化简的结果计算即可．
【详解】
令k，则a=2k，b=3k，∴原式=1．
故答案为：1．
【点睛】
本题考查了约分，解题的关键是掌握约分的定义：约去分式的分子与分母的公因式，不改变分式的值，这样的分式变形叫做分式的约分．
15、5或
【解析】
分析：由菱形的性质证出△ABD是等边三角形，得出BD=AB=6，由勾股定理得出，即可得出答案．
详解：∵四边形ABCD是菱形，
∴AB=AD=6，AC⊥BD，OB=OD，OA=OC，
∵
∴△ABD是等边三角形，
∴BD=AB=6，
∴
∴
∴
∵点E在AC上,
∴当E在点O左边时
当点E在点O右边时
∴或；
故答案为或.
点睛：考查菱形的性质，注意分类讨论思想在数学中的应用，不要漏解.
16、4.4×1
【解析】
科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数．
【详解】
4400000000的小数点向左移动9位得到4.4，
所以4400000000用科学记数法可表示为：4.4×1，
故答案为4.4×1．
【点睛】
本题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
三、解答题（共8题，共72分）
17、（Ⅰ）见表格；（Ⅱ）折线图；（Ⅲ）60%、之前每年增加的百分比依次为 7%、6%、5%、4%，据此预测 2019 年增加的百分比接近 3%．
【解析】
（Ⅰ）根据百分比的意义解答可得；（Ⅱ）根据折线图和扇形图的特点选择即可得；（Ⅲ）根据之前每年增加的百分比依次为7%、6%、5%、4%，据此预测 2019 年增加的百分比接近3% ．
【详解】
（Ⅰ）
（Ⅱ）为了更直观地显示动车组发送旅客量占比的变化趋势，需要用折线图进行描述，
故答案为折线图；
（Ⅲ）预估 2019 年春运期间动车组发送旅客量占比约为 60%，
预估理由是之前每年增加的百分比依次为 7%、6%、5%、4%，据此预测 2019 年增加的百分比接近 3%．
【点睛】
本题考查了统计图的选择，根据统计图的特点正确选择统计图是解题的关键．
18、8+6．
【解析】
如图作CH⊥AB于H．在Rt△BHC求出CH、BH，在Rt△ACH中求出AH、AC即可解决问题；
【详解】
解：如图作CH⊥AB于H．
在Rt△BCH中，∵BC＝12，∠B＝30°，
∴CH＝BC＝6，BH＝＝6，
在Rt△ACH中，tanA＝＝，
∴AH＝8，
∴AC＝＝10，
【点睛】
本题考查解直角三角形，锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．
19、（1）证明见解析；（2）补图见解析；．
【解析】
根据等腰三角形的性质得到，等量代换得到，根据余角的性质即可得到结论；
根据平行线的判定定理得到AD∥BG，推出四边形ABGD是平行四边形，得到平行四边形ABGD是菱形，设AB=BG=GD=AD=x，解直角三角形得到 ，过点B作 于H，根据平行四边形的面积公式即可得到结论．
【详解】
解：，
，
，
，
，
，
，
，
；
补全图形，如图所示：
，，
，，
，，
，
，，且，
，
，
，
四边形ABGD是平行四边形，
，
平行四边形ABGD是菱形，
设，
，
，
，
过点B作于H，
．
．
故答案为（1）证明见解析；（2）补图见解析；．
【点睛】
本题考查等腰三角形的性质，平行四边形的判定和性质，菱形的判定和性质，解题的关键是正确的作出辅助线．
20、（1）；（2）.
【解析】
（1）既是中心对称图形又是轴对称图形只有圆一个图形，然后根据概率的意义解答即可；
（2）画出树状图，然后根据概率公式列式计算即可得解．
【详解】
（1）∵正三角形、平行四边形、圆、正五边形中只有圆既是中心对称图形又是轴对称图形，
∴抽到的卡片既是中心对称图形又是轴对称图形的概率是；
（2）根据题意画出树状图如下：
一共有12种情况，抽出的两张卡片的图形是中心对称图形的是B、C共有2种情况，
所以，P（抽出的两张卡片的图形是中心对称图形）．
【点睛】
本题考查了列表法和树状图法，用到的知识点为：概率=所求情况数与总情况数之比．
21、（1）BC=BD+CE，（2）；（3）.
【解析】
（1）证明△ADB≌△EAC，根据全等三角形的性质得到BD=AC，EC=AB，即可得到BC、BD、CE之间的数量关系;
（2）过D作DE⊥AB，交BA的延长线于E，证明△ABC≌△DEA，得到DE=AB=2，AE=BC=4，Rt△BDE中，BE=6，根据勾股定理即可得到BD的长；
（3）过D作DE⊥BC于E，作DF⊥AB于F，证明△CED≌△AFD，根据全等三角形的性质得到CE=AF，ED=DF，设AF=x，DF=y，根据CB=4，AB=2，列出方程组，求出
的值，根据勾股定理即可求出BD的长.
【详解】
解：（1）观察猜想
结论： BC=BD+CE，理由是：
如图①，∵∠B=90°，∠DAE=90°，
∴∠D+∠DAB=∠DAB+∠EAC=90°，
∴∠D=∠EAC，
∵∠B=∠C=90°，AD=AE，
∴△ADB≌△EAC，
∴BD=AC，EC=AB，
∴BC=AB+AC=BD+CE；
（2）问题解决
如图②，过D作DE⊥AB，交BA的延长线于E，
由（1）同理得：△ABC≌△DEA，
∴DE=AB=2，AE=BC=4，
Rt△BDE中，BE=6，
由勾股定理得：
（3）拓展延伸
如图③，过D作DE⊥BC于E，作DF⊥AB于F，
同理得：△CED≌△AFD，
∴CE=AF，ED=DF，
设AF=x，DF=y，
则，解得：
∴BF=2+1=3，DF=3，
由勾股定理得：
【点睛】
考查全等三角形的判定与性质，勾股定理，二元一次方程组的应用，熟练掌握全等三角形的判定与性质是解题的关键.
22、大和尚有25人，小和尚有75人．
【解析】
设大和尚有x人，小和尚有y人，根据100个和尚吃100个馒头且1个大和尚分3个、3个小和尚分1个，即可得出关于x，y的二元一次方程组，解之即可得出结论．
【详解】
解：设大和尚有x人，小和尚有y人，
依题意，得：，
解得：．
答：大和尚有25人，小和尚有75人．
【点睛】
考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．
23、（1）（1）S=﹣m1﹣4m+4（﹣4＜m＜0）（3）（﹣3，1）、（，﹣1）、（，﹣1）
【解析】
（1）把点A的坐标代入抛物线的解析式，就可求得抛物线的解析式，根据A，C两点的坐标，可求得直线AC的函数解析式；
（1）先过点D作DH⊥x轴于点H，运用割补法即可得到：四边形OCDA的面积=△ADH的面积+四边形OCDH的面积，据此列式计算化简就可求得S关于m的函数关系；
（3）由于AC确定，可分AC是平行四边形的边和对角线两种情况讨论，得到点E与点C的纵坐标之间的关系，然后代入抛物线的解析式，就可得到满足条件的所有点E的坐标．
【详解】
（1）∵A（﹣4，0）在二次函数y=ax1﹣x+1（a≠0）的图象上，
∴0=16a+6+1，
解得a=﹣，
∴抛物线的函数解析式为y=﹣x1﹣x+1；
∴点C的坐标为（0，1），
设直线AC的解析式为y=kx+b，则
，
解得，
∴直线AC的函数解析式为：；
（1）∵点D（m，n）是抛物线在第二象限的部分上的一动点，
∴D（m，﹣m1﹣m+1），
过点D作DH⊥x轴于点H，则DH=﹣m1﹣m+1，AH=m+4，HO=﹣m，
∵四边形OCDA的面积=△ADH的面积+四边形OCDH的面积，
∴S=（m+4）×（﹣m1﹣m+1）+（﹣m1﹣m+1+1）×（﹣m），
化简，得S=﹣m1﹣4m+4（﹣4＜m＜0）；
（3）①若AC为平行四边形的一边，则C、E到AF的距离相等，
∴|yE|=|yC|=1，
∴yE=±1．
当yE=1时，解方程﹣x1﹣x+1=1得，
x1=0，x1=﹣3，
∴点E的坐标为（﹣3，1）；
当yE=﹣1时，解方程﹣x1﹣x+1=﹣1得，
x1=，x1=，
∴点E的坐标为（，﹣1）或（，﹣1）；
②若AC为平行四边形的一条对角线，则CE∥AF，
∴yE=yC=1，
∴点E的坐标为（﹣3，1）．
综上所述，满足条件的点E的坐标为（﹣3，1）、（，﹣1）、（，﹣1）．
24、（1）证明见解析；（2）证明见解析．
【解析】
试题分析：（1）连接OE，AE，由AB是⊙O的直径，得到∠AEB=∠AEC=90°，根据四边形ABCD是平行四边形，得到PA=PC推出∠OEP=∠OAC=90°，根据切线的判定定理即可得到结论；
（2）由AB是⊙O的直径，得到∠AQB=90°根据相似三角形的性质得到=PB•PQ，根据全等三角形的性质得到PF=PE，求得PA=PE=EF，等量代换即可得到结论．
试题解析：（1）连接OE，AE，∵AB是⊙O的直径，∴∠AEB=∠AEC=90°，∵四边形ABCD是平行四边形，∴PA=PC，∴PA=PC=PE，∴∠PAE=∠PEA，∵OA=OE，∴∠OAE=∠OEA，∴∠OEP=∠OAC=90°，∴EF是⊙O的切线；
（2）∵AB是⊙O的直径，∴∠AQB=90°，∴△APQ∽△BPA，∴，∴=PB•PQ，在△AFP与△CEP中，∵∠PAF=∠PCE，∠APF=∠CPE，PA=PC，∴△AFP≌△CEP，∴PF=PE，∴PA=PE=EF，∴=4BP•QP．
考点：切线的判定；平行四边形的性质；相似三角形的判定与性质．
年份
2014
2015
2016
2017
2018
动车组发送旅客量 a 亿人次
0.87
1.14
1.46
1.80
2.17
铁路发送旅客总量 b 亿人次
2.52
2.76
3.07
3.42
3.82
动车组发送旅客量占比× 100
34.5 %
41.3 %
47.6 %
52.6 %
56.8 %