江苏省南京市江宁区2022年初中数学毕业考试模拟冲刺卷含解析

这是一份江苏省南京市江宁区2022年初中数学毕业考试模拟冲刺卷含解析，共18页。试卷主要包含了考生必须保证答题卡的整洁等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1．估计的值在（　　）
A．4和5之间 B．5和6之间 C．6和7之间 D．7和8之间
2．下列几何体中，三视图有两个相同而另一个不同的是（　　）

A．（1）（2） B．（2）（3） C．（2）（4） D．（3）（4）
3．已知圆内接正三角形的面积为3，则边心距是（　　）
A．2 B．1 C． D．
4．如图，已知，那么下列结论正确的是（ ）

A． B． C． D．
5．若正比例函数y＝kx的图象上一点（除原点外）到x轴的距离与到y轴的距离之比为3，且y值随着x值的增大而减小，则k的值为（　　）
A．﹣ B．﹣3 C． D．3
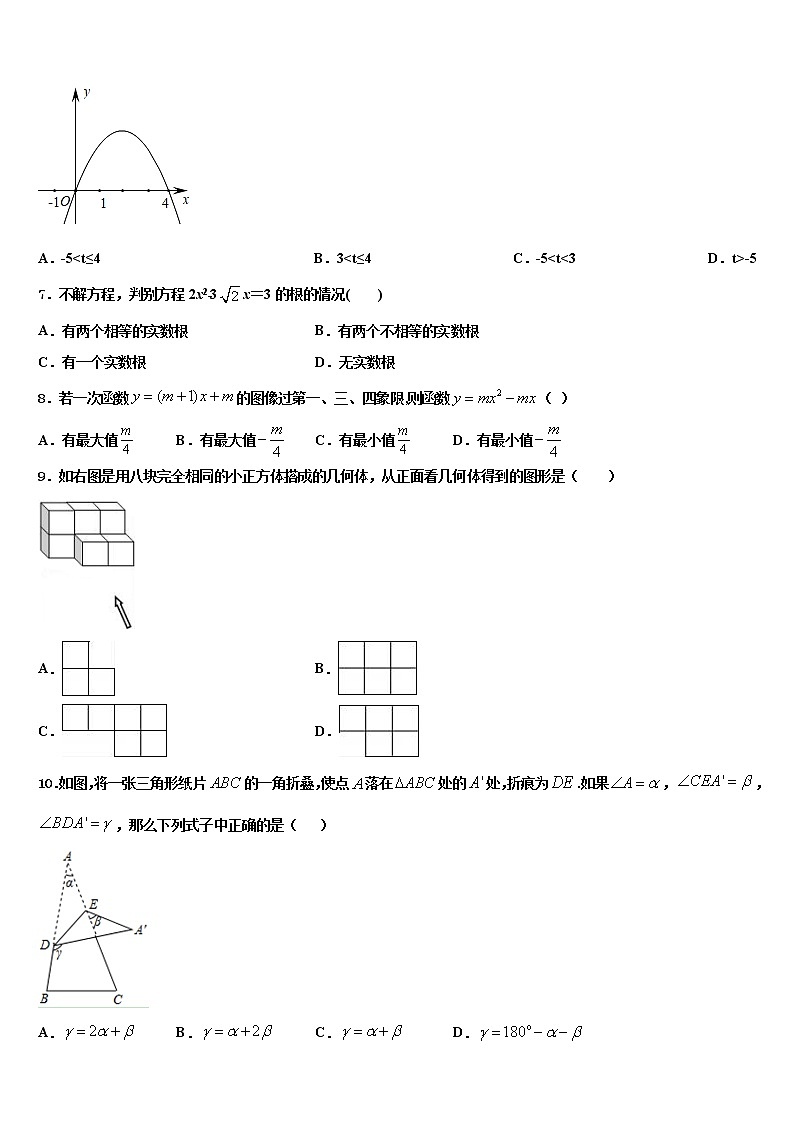
6．如图，抛物线y=-x2+mx的对称轴为直线x=2，若关于x的-元二次方程-x2+mx-t=0 (t为实数)在l
A．-5-5
7．不解方程，判别方程2x2﹣3x＝3的根的情况(　　)
A．有两个相等的实数根 B．有两个不相等的实数根
C．有一个实数根 D．无实数根
8．若一次函数的图像过第一、三、四象限,则函数（ ）
A．有最大值 B．有最大值 C．有最小值 D．有最小值
9．如右图是用八块完全相同的小正方体搭成的几何体，从正面看几何体得到的图形是（ ）

A． B．
C． D．
10．如图，将一张三角形纸片的一角折叠，使点落在处的处，折痕为.如果，，，那么下列式子中正确的是（ ）

A． B． C． D．
二、填空题（共7小题，每小题3分，满分21分）
11．如图，△ABC中，过重心G的直线平行于BC，且交边AB于点D，交边AC于点E，如果设=，=，用，表示，那么=___．

12．化简的结果等于__．
13．使有意义的x的取值范围是______．
14．如图，将一块含有30°角的直角三角板的两个顶点叠放在长方形的两条对边上，如果∠1=27°，那么∠2=______°

15．小明掷一枚均匀的骰子，骰子的六个面上分别刻有1，2，3，4，5，6点，得到的点数为奇数的概率是 ．
16．不等式-2x+3>0的解集是___________________
17．从﹣2，﹣1，2，0这四个数中任取两个不同的数作为点的坐标，该点不在第三象限的概率是_____．
三、解答题（共7小题，满分69分）
18．（10分）抛物线y=﹣x2+（m﹣1）x+m与y轴交于（0，3）点．

（1）求出m的值并画出这条抛物线；
（2）求它与x轴的交点和抛物线顶点的坐标；
（3）x取什么值时，抛物线在x轴上方？
（4）x取什么值时，y的值随x值的增大而减小？
19．（5分）如图，在△ABC中，∠ABC=90°，BD为AC边上的中线．
（1）按如下要求尺规作图，保留作图痕迹，标注相应的字母：过点C作直线CE，使CE⊥BC于点C，交BD的延长线于点E，连接AE；
（2）求证：四边形ABCE是矩形．

20．（8分）如图，直线y=kx+b（k≠0）与双曲线y=（m≠0）交于点A（﹣，2），B（n，﹣1）．求直线与双曲线的解析式．点P在x轴上，如果S△ABP=3，求点P的坐标．

21．（10分）已知：在△ABC中，AC=BC，D，E，F分别是AB，AC，CB的中点.
　　求证：四边形DECF是菱形.
22．（10分）立定跳远是嘉兴市体育中考的抽考项目之一，某校九年级（1），（2）班准备集体购买某品牌的立定跳远训练鞋．现了解到某网店正好有这种品牌训练鞋的促销活动，其购买的单价y（元/双）与一次性购买的数量x（双）之间满足的函数关系如图所示．当10≤x＜60时，求y关于x的函数表达式；九（1），（2）班共购买此品牌鞋子100双，由于某种原因需分两次购买，且一次购买数量多于25双且少于60双；
①若两次购买鞋子共花费9200元，求第一次的购买数量；
②如何规划两次购买的方案，使所花费用最少，最少多少元？

23．（12分） 某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，如图是水平放置的破裂管道有水部分的截面．
(1)请你用直尺和圆规作出这个输水管道的圆形截面的圆心(保留作图痕迹)；
(2)若这个输水管道有水部分的水面宽AB＝8 cm，水面最深地方的高度为2 cm，求这个圆形截面的半径．

24．（14分）在平面直角坐标系xOy中，若抛物线顶点A的横坐标是，且与y轴交于点，点P为抛物线上一点．
求抛物线的表达式；
若将抛物线向下平移4个单位，点P平移后的对应点为如果，求点Q的坐标．




参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1、C
【解析】
∵ ，
∴.
即的值在6和7之间.
故选C.
2、B
【解析】
根据三视图的定义即可解答．
【详解】
正方体的三视图都是正方形，故（1）不符合题意；
圆柱的主视图、左视图都是矩形，俯视图是圆，故（2）符合题意；
圆锥的主视图、左视图都是三角形，俯视图是圆形，故（3）符合题意；
三棱锥主视图是、左视图是，俯视图是三角形，故（4）不符合题意；
故选B．
【点睛】
本题考查了简单几何体的三视图，熟知三视图的定义是解决问题的关键.
3、B
【解析】
根据题意画出图形，连接AO并延长交BC于点D，则AD⊥BC，设OD=x，由三角形重心的性质得AD=3x， 利用锐角三角函数表示出BD的长，由垂径定理表示出BC的长，然后根据面积法解答即可．
【详解】
如图，

连接AO并延长交BC于点D，则AD⊥BC，
设OD=x，则AD=3x，
∵tan∠BAD=，
∴BD= tan30°·AD=x，
∴BC=2BD=2x，
∵ ,
∴×2x×3x=3，
∴x＝1
所以该圆的内接正三边形的边心距为1，
故选B．
【点睛】
本题考查正多边形和圆，三角形重心的性质，垂径定理，锐角三角函数，面积法求线段的长，解答本题的关键是明确题意，求出相应的图形的边心距．
4、A
【解析】
已知AB∥CD∥EF，根据平行线分线段成比例定理，对各项进行分析即可．
【详解】
∵AB∥CD∥EF，
∴．
故选A．
【点睛】
本题考查平行线分线段成比例定理，找准对应关系，避免错选其他答案．
5、B
【解析】
设该点的坐标为（a，b），则|b|=1|a|，利用一次函数图象上的点的坐标特征可得出k=±1，再利用正比例函数的性质可得出k=-1，此题得解．
【详解】
设该点的坐标为（a，b），则|b|＝1|a|，
∵点（a，b）在正比例函数y＝kx的图象上，
∴k＝±1．
又∵y值随着x值的增大而减小，
∴k＝﹣1．
故选：B．
【点睛】
本题考查了一次函数图象上点的坐标特征以及正比例函数的性质，利用一次函数图象上点的坐标特征，找出k=±1是解题的关键．
6、B
【解析】
先利用抛物线的对称轴方程求出m得到抛物线解析式为y=-x2+4x，配方得到抛物线的顶点坐标为（2，4），再计算出当x=1或3时，y=3，结合函数图象，利用抛物线y=-x2+4x与直线y=t在1＜x＜3的范围内有公共点可确定t的范围．
【详解】
∵ 抛物线y=-x2+mx的对称轴为直线x=2，
∴，
解之：m=4，
∴y=-x2+4x，
当x=2时，y=-4+8=4，
∴顶点坐标为(2，4)，
∵ 关于x的-元二次方程-x2+mx-t=0 (t为实数)在l 当x=1时，y=-1+4=3，
当x=2时，y=-4+8=4，
∴ 3 故选：B
【点睛】
本题考查了抛物线与x轴的交点：把求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程．也考查了二次函数的性质．
7、B
【解析】
一元二次方程的根的情况与根的判别式有关，
，方程有两个不相等的实数根，故选B
8、B
【解析】
解：∵一次函数y=（m+1）x+m的图象过第一、三、四象限，
∴m+1＞0，m＜0，即-1＜m＜0，
∴函数有最大值，
∴最大值为，
故选B．
9、B
【解析】
找到从正面看所得到的图形即可，注意所有从正面看到的棱都应表现在主视图中.
【详解】
解：从正面看该几何体，有3列正方形，分别有：2个，2个，2个，如图.

故选B．
【点睛】
本题考查了三视图的知识，主视图是从物体的正面看到的视图，属于基础题型.
10、A
【解析】
分析:根据三角形的外角得：∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，代入已知可得结论.
详解:

由折叠得：∠A=∠A'，
∵∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，
∵∠A=α，∠CEA′=β，∠BDA'=γ，
∴∠BDA'=γ=α+α+β=2α+β，
故选A.
点睛：本题考查了三角形外角的性质，熟练掌握三角形的外角等于与它不相邻的两个内角的和是关键.

二、填空题（共7小题，每小题3分，满分21分）
11、
【解析】
连接AG，延长AG交BC于F．首先证明DG=GE，再利用三角形法则求出即可解决问题．
【详解】
连接AG，延长AG交BC于F．

∵G是△ABC的重心，DE∥BC，
∴BF=CF，
，
∵，，
∴，
∵BF=CF，
∴DG=GE，
∵，，
∴，
∴，
故答案为．
【点睛】
本题考查三角形的重心，平行线的性质，平面向量等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
12、．
【解析】
先通分变为同分母分式，然后根据分式的减法法则计算即可．
【详解】
解：原式


．
故答案为：．
【点睛】
此题考查的是分式的减法，掌握分式的减法法则是解决此题的关键．
13、
【解析】
二次根式有意义的条件．
【分析】根据二次根式被开方数必须是非负数的条件，要使在实数范围内有意义，必须．
14、57°.
【解析】
根据平行线的性质和三角形外角的性质即可求解.
【详解】
由平行线性质及外角定理，可得∠2＝∠1+30°=27°+30°=57°.
【点睛】
本题考查平行线的性质及三角形外角的性质.
15、．
【解析】
根据题意可知，掷一次骰子有6个可能结果，而点数为奇数的结果有3个，所以点数为奇数的概率为．
考点：概率公式．
16、x<
【解析】
根据解一元一次不等式基本步骤：移项、系数化为1可得．
【详解】
移项，得：-2x＞-3，
系数化为1，得：x＜，
故答案为x＜．
【点睛】
本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．
17、
【解析】
列举出所有情况，看在第四象限的情况数占总情况数的多少即可．
【详解】
如图：

共有12种情况，在第三象限的情况数有2种，
故不再第三象限的共10种，
不在第三象限的概率为，
故答案为．
【点睛】
本题考查了树状图法的知识，解题的关键是列出树状图求出概率．

三、解答题（共7小题，满分69分）
18、（1）；（2），；（1）；（2）
【解析】
试题分析：（1）由抛物线y=﹣x2+（m﹣1）x+m与y轴交于（0，1）得：m=1．
∴抛物线为y=﹣x2+2x+1=﹣（x﹣1）2+2．
列表得：

X

﹣1


0


1


2


1


y


0


1


2


1


0

图象如下．

（2）由﹣x2+2x+1=0，得：x1=﹣1，x2=1．
∴抛物线与x轴的交点为（﹣1，0），（1，0）．
∵y=﹣x2+2x+1=﹣（x﹣1）2+2
∴抛物线顶点坐标为（1，2）．
（1）由图象可知：
当﹣1＜x＜1时，抛物线在x轴上方．
（2）由图象可知：
当x＞1时，y的值随x值的增大而减小
考点: 二次函数的运用
19、 (1)见解析;(2)见解析.
【解析】
（1）根据题意作图即可；
（2）先根据BD为AC边上的中线，AD=DC，再证明△ABD≌△CED（AAS）得AB=EC，已知∠ABC=90°即可得四边形ABCE是矩形．
【详解】
（1）解：如图所示：E点即为所求；

（2）证明：∵CE⊥BC，
∴∠BCE=90°，
∵∠ABC=90°，
∴∠BCE+∠ABC=180°，
∴AB∥CE，
∴∠ABE=∠CEB，∠BAC=∠ECA，
∵BD为AC边上的中线，
∴AD=DC，
在△ABD和△CED中
，
∴△ABD≌△CED（AAS），
∴AB=EC，
∴四边形ABCE是平行四边形，
∵∠ABC=90°，
∴平行四边形ABCE是矩形．
【点睛】
本题考查了全等三角形的判定与性质与矩形的性质，解题的关键是熟练的掌握全等三角形的判定与性质与矩形的性质.
20、（1）y=﹣2x+1；（2）点P的坐标为（﹣，0）或（，0）．
【解析】
（1）把A的坐标代入可求出m，即可求出反比例函数解析式，把B点的坐标代入反比例函数解析式，即可求出n，把A，B的坐标代入一次函数解析式即可求出一次函数解析式；
（2）利用一次函数图象上点的坐标特征可求出点C的坐标，设点P的坐标为(x,0)，根据三角形的面积公式结合S△ABP=3，即可得出，解之即可得出结论．
【详解】
（1）∵双曲线y=（m≠0）经过点A（﹣，2），
∴m=﹣1．
∴双曲线的表达式为y=﹣．
∵点B（n，﹣1）在双曲线y=﹣上，
∴点B的坐标为（1，﹣1）．
∵直线y=kx+b经过点A（﹣，2），B（1，﹣1），
∴，解得
∴直线的表达式为y=﹣2x+1；
（2）当y=﹣2x+1=0时，x=，
∴点C（，0）．
设点P的坐标为（x，0），
∵S△ABP=3，A（﹣，2），B（1，﹣1），
∴×3|x﹣|=3，即|x﹣|=2，
解得：x1=﹣，x2=．
∴点P的坐标为（﹣，0）或（，0）．
【点睛】
本题考查了反比例函数与一次函数的交点问题、一次（反比例）函数图象上点的坐标特征、待定系数法求一次函数、反比例函数的解析式以及三角形的面积，解题的关键是：（1）根据点的坐标利用待定系数法求出函数的解析式；（2）根据三角形的面积公式以及S△ABP=3，得出．
21、见解析
【解析】
证明：∵D、E是AB、AC的中点
　　∴DE=BC，EC=AC
　　∵D、F是AB、BC的中点
　　∴DF=AC，FC=BC
　　∴DE=FC=BC，EC=DF=AC
　　∵AC=BC
　　∴DE=EC=FC=DF
　　∴四边形DECF是菱形
22、（1）y＝150﹣x； （2）①第一批购买数量为30双或40双．②第一次买26双，第二次买74双最省钱，最少9144元．
【解析】
（1）若购买x双（10＜x＜1），每件的单价＝140﹣（购买数量﹣10），依此可得y关于x的函数关系式；
（2）①设第一批购买x双，则第二批购买（100﹣x）双，根据购买两批鞋子一共花了9200元列出方程求解即可．分两种情况考虑：当25＜x≤40时，则1≤100﹣x＜75；当40＜x＜1时，则40＜100﹣x＜1．
②把两次的花费与第一次购买的双数用函数表示出来．
【详解】
解：（1）购买x双（10＜x＜1）时，y＝140﹣（x﹣10）＝150﹣x．
故y关于x的函数关系式是y＝150﹣x；
（2）①设第一批购买x双，则第二批购买（100﹣x）双．
当25＜x≤40时，则1≤100﹣x＜75，则x（150﹣x）+80（100﹣x）＝9200，
解得x1＝30，x2＝40；
当40＜x＜1时，则40＜100﹣x＜1，
则x（150﹣x）+（100﹣x）[150﹣（100﹣x）]＝9200，
解得x＝30或x＝70，但40＜x＜1，所以无解；
答：第一批购买数量为30双或40双．
②设第一次购买x双，则第二次购买（100﹣x）双，设两次花费w元．
当25＜x≤40时w＝x（150﹣x）+80（100﹣x）＝﹣（x﹣35）2+9225，
∴x＝26时，w有最小值，最小值为9144元；
当40＜x＜1时，
w＝x（150﹣x）+（100﹣x）[150﹣（100﹣x）]＝﹣2（x﹣50）2+10000，
∴x＝41或59时，w有最小值，最小值为9838元，
综上所述：第一次买26双，第二次买74双最省钱，最少9144元．
【点睛】
考查了一元二次方程的应用，根据实际问题列一次函数关系式，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．
23、（1）详见解析；（2）这个圆形截面的半径是5 cm.
【解析】
（1）根据尺规作图的步骤和方法做出图即可；
（2）先过圆心作半径，交于点，设半径为，得出、的长，在中，根据勾股定理求出这个圆形截面的半径.
【详解】
(1)如图，作线段AB的垂直平分线l，与弧AB交于点C，作线段AC的垂直平分线l′与直线l交于点O，点O即为所求作的圆心．

(2)如图，过圆心O作半径CO⊥AB，交AB于点D，
设半径为r，则AD＝AB＝4，OD＝r－2，
在Rt△AOD中，r2＝42＋(r－2)2，解得r＝5，
答：这个圆形截面的半径是5 cm.
【点睛】
此题考查了垂径定理和勾股定理，关键是根据题意画出图形，再根据勾股定理进行求解.
24、为；点Q的坐标为或．
【解析】
依据抛物线的对称轴方程可求得b的值，然后将点B的坐标代入线可求得c的值,即可求得抛物线的表达式；由平移后抛物线的顶点在x轴上可求得平移的方向和距离，故此，然后由点，轴可得到点Q和P关于x对称，可求得点Q的纵坐标，将点Q的纵坐标代入平移后的解析式可求得对应的x的值，则可得到点Q的坐标．
【详解】
抛物线顶点A的横坐标是，
，即，解得．
．
将代入得：，
抛物线的解析式为．
抛物线向下平移了4个单位．
平移后抛物线的解析式为，．
，
点O在PQ的垂直平分线上．
又轴，
点Q与点P关于x轴对称．
点Q的纵坐标为．
将代入得：，解得：或．
点Q的坐标为或．
【点睛】
本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次函数的解析式、二次函数的平移规律、线段垂直平分线的性质，发现点Q与点P关于x轴对称，从而得到点Q的纵坐标是解题的关键．