
2023届江西省“红色十校”高三上学期第一联考理科数学试题
展开江西“红色十校”2023届高三第一次联考
数学理科
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合, 则
A. B. C. D.
2. 若复数满足, 则的虚部为
A. B. C. -2 D. 2
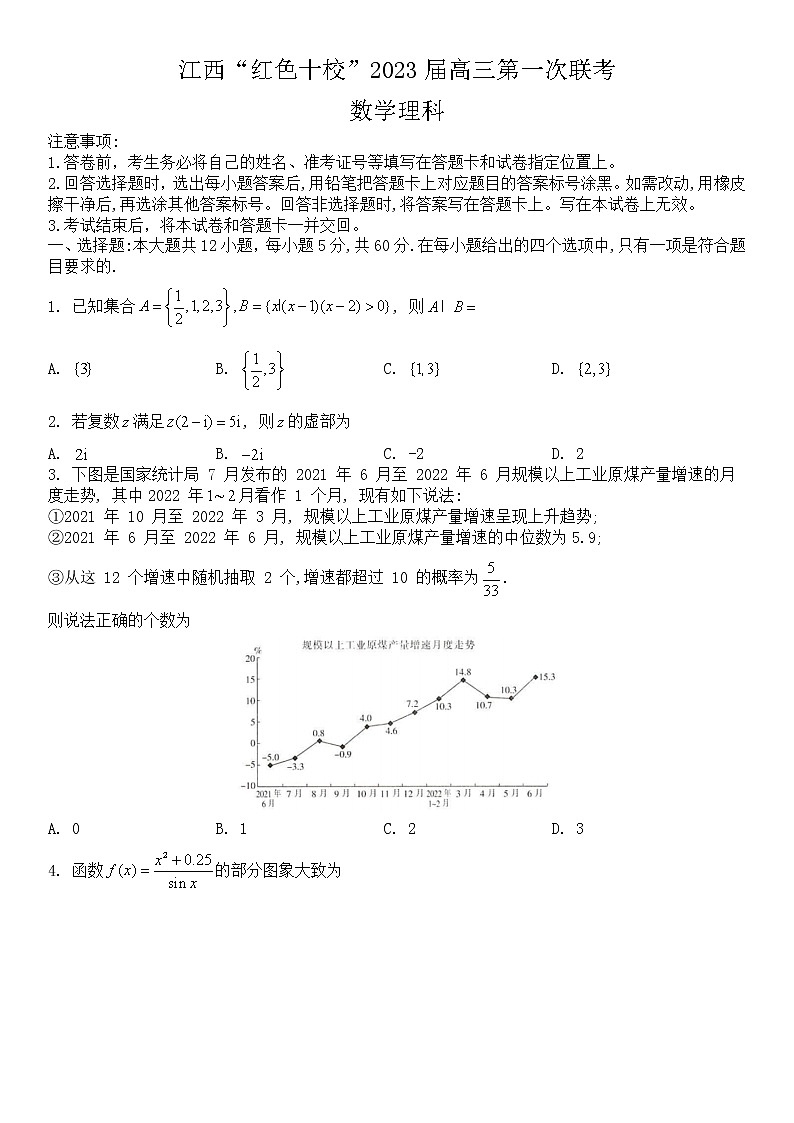
3. 下图是国家统计局 7 月发布的 2021 年 6 月至 2022 年 6 月规模以上工业原煤产量增速的月度走势, 其中2022 年月看作 1 个月, 现有如下说法:
①2021 年 10 月至 2022 年 3 月, 规模以上工业原煤产量增速呈现上升趋势;
②2021 年 6 月至 2022 年 6 月, 规模以上工业原煤产量增速的中位数为5.9;
③从这 12 个增速中随机抽取 2 个,增速都超过 10 的概率为.
则说法正确的个数为
A. 0 B. 1 C. 2 D. 3
4. 函数的部分图象大致为
5. 2022 年 11 月, 第五届中国国际进口博览会在上海举行, 组委员会安排 5 名工作人员去, 等 4 个场馆, 其中场馆安排 2 人, 其余比赛场馆各 1 人, 则不同的安排方法种数为
A. 48 B. 60 C. 120 D. 240
6. 设函数, 若是奇函数, 则
A. B. C. D.
7. 设, 则
A. B. C. D.
8. 将函数的图象上所有点向有平移个单位长度, 得到如图所示的函数的图象, 则
A. 0
B. 1
C. 2
D. -1
9. “寸影千里”法是《周髀算经》中记载的一种远距离测量的估算方法,其具体方法是在同一天(如夏至)的正午,于两地分别竖起同高的标杆,然后测量标杆的影长,并根据“日影差一寸,实地相距千里”的原则推算两地距离.如图,某人在夏至的正午分别在同一水平面上的两地竖起高度均为寸的标的差结合 “寸影千里” 来推算两地的距离. 记, 则按照 “寸影千里” 的原则, 两地的距离大约为
A. 里
B. 里
C. 里
D. 里
10. 已知, 满足, 则的是小值是
A. B. C. D.
11. 已知三棱锥的顶点都在球的球面上,, 若三棱锥的体积最大值为 2 , 则球的半径为
A. B. C. D.
12. 若曲线与曲线在公共点处有公共切线, 则实数
A. B. C. D.
二、填空题: 本大题共 4 小题,每小题 5 分,共 20 分.
13. 已知向量, 且, 则实数______.
14. 已知拋物线的焦点为,点到直线的距离为 , 则的 值为______.
15. 已知, 则______, 的最小值是______. (第一空 2 分,第二空 3 分)
16. 韩信是我国汉代能征善战、智勇双全的一员大将. 历史上流传着一个关于他点兵的奇特方法. 有一天,韩信问有多少士兵在操练, 部将回答:三三数之,剩二;五五数之,剩三;七七七数之,剩四,韩信很快就知道了士兵的人数. 设有个士兵,若,符合条件的共有______.
三、解答题: 共 70 分. 解答应写出文字说明、证明过程或演算步骤. 第题为必考题,每个试题考生都必须作答. 第22、23题为选考题,考生根据要求作答.
(一) 必考题:共 60 分.
17. (12 分) 在①, ②,③这三个条件中任选一个, 填在下面的横线上, 并解答问题.
已知数列的前项和为, 且______.
(1) 求的通项公式;
(2) 若是的等比中项, 求数列的前项和.
注: 如选择多个条件分别解答, 按第一个解答计分.
18. (12 分) 如图, 在四棱锥中,平面, 底面四边形是正方形,, 点为的中点.
(1)求证: 平面;
(2) 求平面与平面所成锐二面角的大小.
19. (12 分)
在中,内角所对的边分别为,且.
(1) 求;
(2) 若, 求和.
20. (12 分) 设为坐标原点, 椭圆的离心率为, 且过点.
(1) 求的方程;
(2) 若直线与交于两点, 且的面积是, 求证:.
21. (12 分) 已知函数.
(1) 求的极值;
(2) 若函数, 求的极小值的最大值.
(二) 选考题: 共 10 分. 请考生在第 22,23 题中任选一题作答. 如果多做, 则按所做的第一题计分.
22. (10 分)【选修4-4:坐标系与参数方程】
在直角坐标系中, 曲线的参数方程为 ( 为参数),以坐标原点为极点, 轴正半轴为极轴建立极坐标系, 直线的极坐标方程为.
(1) 求的极坐标方程和的直角坐标方程;
(2) 与交于两点, 若, 求.
23. (10 分)【选修 4-5: 不等式选讲】
已知函数.
(1) 当时, 求不等式的解集;
(2) 若不等式对和恒成立, 求实数的取值范围.
2023届江西省“红色十校”高三上学期第一联考数学(文)试题含解析: 这是一份2023届江西省“红色十校”高三上学期第一联考数学(文)试题含解析,共15页。试卷主要包含了单选题,填空题,双空题,解答题等内容,欢迎下载使用。
2023届江西省“红色十校”高三上学期第一次联考数学文含答案: 这是一份2023届江西省“红色十校”高三上学期第一次联考数学文含答案
2023届江西省“红色十校”高三上学期第一联考数学(理)试题含答案: 这是一份2023届江西省“红色十校”高三上学期第一联考数学(理)试题含答案,共16页。试卷主要包含了单选题,填空题,双空题,解答题等内容,欢迎下载使用。












