湖南长沙长郡芙蓉中学2022年中考联考数学试卷含解析

这是一份湖南长沙长郡芙蓉中学2022年中考联考数学试卷含解析，共17页。试卷主要包含了下列运算正确的是等内容，欢迎下载使用。
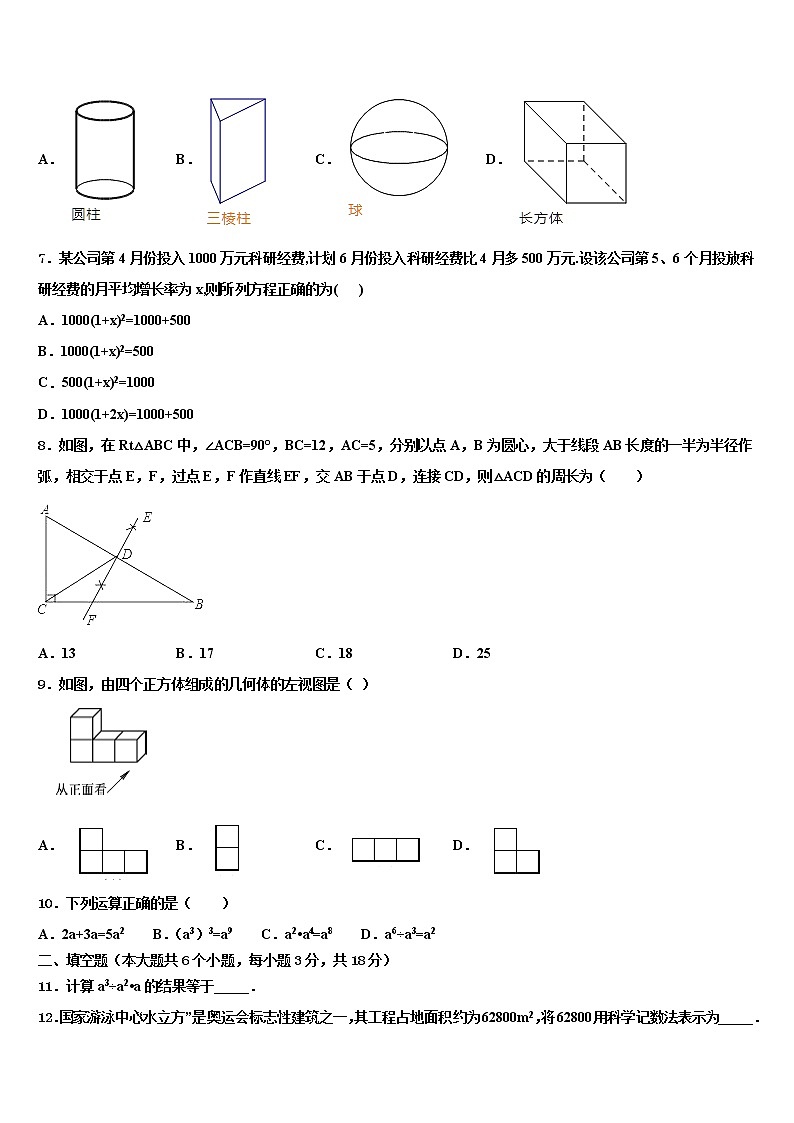
2021-2022中考数学模拟试卷注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗． 一、选择题（共10小题，每小题3分，共30分）1．在下列二次函数中，其图象的对称轴为的是A． B． C． D．2．下列各图中，∠1与∠2互为邻补角的是(   )A． B．C． D．3．的倒数是（    ）A． B．3 C． D．4．我省2013年的快递业务量为1．2亿件，受益于电子商务发展和法治环境改善等多重因素，快递业务迅猛发展，2012年增速位居全国第一．若2015年的快递业务量达到2．5亿件，设2012年与2013年这两年的平均增长率为x，则下列方程正确的是（    ）A．1．2（1＋x）＝2．5B．1．2（1＋2x）＝2．5C．1．2（1＋x）2＝2．5D．1．2（1＋x）＋1．2（1＋x）2＝2．55．1cm2的电子屏上约有细菌135000个，135000用科学记数法表示为（　　）A．0.135×106 B．1.35×105 C．13.5×104 D．135×1036．下列基本几何体中，三视图都是相同图形的是（　　）A． B． C． D．7．某公司第4月份投入1000万元科研经费,计划6月份投入科研经费比4月多500万元.设该公司第5、6个月投放科研经费的月平均增长率为x,则所列方程正确的为(   )A．1000(1+x)2=1000+500B．1000(1+x)2=500C．500(1+x)2=1000D．1000(1+2x)=1000+5008．如图，在Rt△ABC中，∠ACB=90°，BC=12，AC=5，分别以点A，B为圆心，大于线段AB长度的一半为半径作弧，相交于点E，F，过点E，F作直线EF，交AB于点D，连接CD，则△ACD的周长为（　　）A．13 B．17 C．18 D．259．如图，由四个正方体组成的几何体的左视图是（ ）A． B． C． D．10．下列运算正确的是（　　）A．2a+3a=5a2    B．（a3）3=a9    C．a2•a4=a8    D．a6÷a3=a2二、填空题（本大题共6个小题，每小题3分，共18分）11．计算a3÷a2•a的结果等于_____．12．国家游泳中心“水立方”是奥运会标志性建筑之一，其工程占地面积约为62800m2，将62800用科学记数法表示为_____．13．有下列各式：①；②；③；④．其中，计算结果为分式的是_____．（填序号）14．如图，直径为1000mm的圆柱形水管有积水（阴影部分），水面的宽度AB为800mm，则水的最大深度CD是______mm．15．数据：2，5，4，2，2的中位数是_____，众数是_____，方差是_____．16．如图，是用火柴棒拼成的图形，则第n个图形需_____根火柴棒．三、解答题（共8题，共72分）17．（8分）（1）计算：（﹣2）﹣2+cos60°﹣（﹣2）0；（2）化简：（a﹣）÷ ．18．（8分）如图，四边形ABCD的四个顶点分别在反比例函数与(x＞0，0＜m＜n)的图象上，对角线BD//y轴，且BD⊥AC于点P．已知点B的横坐标为1．当m=1，n=20时．①若点P的纵坐标为2，求直线AB的函数表达式．②若点P是BD的中点，试判断四边形ABCD的形状，并说明理由．四边形ABCD能否成为正方形？若能，求此时m，n之间的数量关系；若不能，试说明理由．19．（8分）如图，矩形中，对角线、交于点，以、为邻边作平行四边形，连接求证：四边形是菱形若，，求四边形的面积20．（8分）计算：（1）（2）2﹣|﹣4|+3﹣1×6+20；（2）．21．（8分）一辆高铁与一辆动车组列车在长为1320千米的京沪高速铁路上运行，已知高铁列车比动车组列车平均速度每小时快99千米，且高铁列车比动车组列车全程运行时间少3小时，求这辆高铁列车全程运行的时间和平均速度．22．（10分）如图，AC⊥BD，DE交AC于E，AB＝DE，∠A＝∠D．求证：AC＝AE+BC．23．（12分） “千年古都，大美西安”．某校数学兴趣小组就“最想去的西安旅游景点”随机调查了本校部分学生，要求每位同学选择且只能选择一个最想去的景点，（景点对应的名称分别是：A：大雁塔  B：兵马俑 C：陕西历史博物馆 D：秦岭野生动物园 E：曲江海洋馆）．下面是根据调查结果进行数据整理后绘制出的不完整的统计图：请根据图中提供的信息，解答下列问题：（1）求被调查的学生总人数；（2）补全条形统计图，并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数；（3）若该校共有800名学生，请估计“最想去景点B”的学生人数．24．如图，△ABC和△BEC均为等腰直角三角形，且∠ACB＝∠BEC＝90°，AC＝4，点P为线段BE延长线上一点，连接CP以CP为直角边向下作等腰直角△CPD，线段BE与CD相交于点F．（1）求证：；（2）连接BD，请你判断AC与BD有什么位置关系？并说明理由；（3）若PE＝1，求△PBD的面积．


参考答案 一、选择题（共10小题，每小题3分，共30分）1、A【解析】y=（x+2）2的对称轴为x=–2，A正确；y=2x2–2的对称轴为x=0，B错误；y=–2x2–2的对称轴为x=0，C错误；y=2（x–2）2的对称轴为x=2，D错误．故选A．1．2、D【解析】根据邻补角的定义可知：只有D图中的是邻补角，其它都不是．故选D．3、A【解析】
解：的倒数是．故选A．【点睛】本题考查倒数，掌握概念正确计算是解题关键．4、C【解析】试题解析：设2015年与2016年这两年的平均增长率为x，由题意得：1.2（1+x）2=2.5，故选C．5、B【解析】
根据科学记数法的表示形式（a×10n的形式，其中1≤|a|＜10，n为整数，确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同；当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数）．【详解】解：135000用科学记数法表示为：1.35×1．故选B．【点睛】科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．6、C【解析】
根据主视图、左视图、俯视图的定义，可得答案．【详解】球的三视图都是圆，故选C．【点睛】本题考查了简单几何体的三视图，熟记特殊几何体的三视图是解题关键．7、A【解析】
设该公司第5、6个月投放科研经费的月平均增长率为x，5月份投放科研经费为1000（1+x），6月份投放科研经费为1000（1+x）（1+x），即可得答案.【详解】设该公司第5、6个月投放科研经费的月平均增长率为x，则6月份投放科研经费1000（1+x）2=1000+500，故选A.【点睛】考查一元二次方程的应用，求平均变化率的方法为：若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b．8、C【解析】在Rt△ABC中，∠ACB=90°，BC=12，AC=5，根据勾股定理求得AB=13.根据题意可知，EF为线段AB的垂直平分线，在Rt△ABC中，根据直角三角形斜边的中线等于斜边的一半可得CD=AD=AB，所以△ACD的周长为AC+CD+AD=AC+AB=5+13=18.故选C.9、B【解析】从左边看可以看到两个小正方形摞在一起，故选B.10、B【解析】
直接利用同底数幂的乘除运算法则以及幂的乘方运算法则、合并同类项法则分别化简得出答案．【详解】A、2a+3a=5a，故此选项错误；B、（a3）3=a9，故此选项正确；C、a2•a4=a6，故此选项错误；D、a6÷a3=a3，故此选项错误．故选：B．【点睛】此题主要考查了同底数幂的乘除运算以及合并同类项和幂的乘方运算，正确掌握运算法则是解题关键． 二、填空题（本大题共6个小题，每小题3分，共18分）11、a1【解析】
根据同底数幂的除法法则和同底数幂乘法法则进行计算即可．【详解】解：原式=a3﹣1+1=a1．故答案为a1．【点睛】本题考查了同底数幂的乘除法，关键是掌握计算法则．12、6.28×1．【解析】
科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【详解】62800用科学记数法表示为6.28×1．故答案为6.28×1．【点睛】此题主要考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．13、②④【解析】
根据分式的定义，将每个式子计算后，即可求解.【详解】=1不是分式，=，=3不是分式，=故选②④.【点睛】本题考查分式的判断，解题的关键是清楚分式的定义.14、200【解析】
先求出OA的长，再由垂径定理求出AC的长，根据勾股定理求出OC的长，进而可得出结论．【详解】解：∵⊙O的直径为1000mm，
∴OA=OA=500mm．
∵OD⊥AB，AB=800mm，
∴AC=400mm，
∴OC== =300mm，  ∴CD=OD-OC=500-300=200（mm）．
答：水的最大深度为200mm．故答案为：200【点睛】本题考查的是垂径定理的应用，根据勾股定理求出OC的长是解答此题的关键．15、2    2    1.1．    【解析】
先将这组数据从小到大排列，再找出最中间的数，即可得出中位数；找出这组数据中最多的数则是众数；先求出这组数据的平均数，再根据方差公式S2=[（x1-）2+（x2-）2+…+（xn-）2]进行计算即可．【详解】解：把这组数据从小到大排列为：2，2，2，4，5，最中间的数是2，则中位数是2；众数为2；∵这组数据的平均数是(2+2+2+4+5)÷5=3，∴方差是： [(2−3)2+(2−3)2+(2−3)2+(4−3)2+(5−3)2]=1.1.故答案为2，2，1.1.【点睛】本题考查了中位数、众数与方差的定义，解题的关键是熟练的掌握中位数、众数与方差的定义.16、2n+1．【解析】
解：根据图形可得出：当三角形的个数为1时，火柴棒的根数为3；当三角形的个数为2时，火柴棒的根数为5；当三角形的个数为3时，火柴棒的根数为7；当三角形的个数为4时，火柴棒的根数为9；……由此可以看出：当三角形的个数为n时，火柴棒的根数为3+2（n﹣1）=2n+1．故答案为：2n+1． 三、解答题（共8题，共72分）17、（1）；（2）；【解析】
（1）根据负整数指数幂、特殊角的三角函数值、零指数幂可以解答本题；（2）根据分式的减法和除法可以解答本题．【详解】解：（1）原式 （2）原式 【点睛】本题考查分式的混合运算、实数的运算、负整数指数幂、特殊角的三角函数值、零指数幂，解答本题的关键是明确它们各自的计算方法．18、（1）①；②四边形是菱形，理由见解析；（2）四边形能是正方形，理由见解析，m+n=32.【解析】
（1）①先确定出点A，B坐标，再利用待定系数法即可得出结论；
②先确定出点D坐标，进而确定出点P坐标，进而求出PA，PC，即可得出结论；
（2）先确定出B（1，），D（1，），进而求出点P的坐标，再求出A，C坐标，最后用AC=BD，即可得出结论．【详解】（1）①如图1，，反比例函数为，当时，，，当时，，，，设直线的解析式为， ， ，直线的解析式为；②四边形是菱形，理由如下：如图2，由①知，，轴，，点是线段的中点，，当时，由得，，由得，，，，，，四边形为平行四边形，，四边形是菱形；（2）四边形能是正方形，理由：当四边形是正方形，记，的交点为，,当时，，，，，，，，， ，.【点睛】此题是反比例函数综合题，主要考查了待定系数法，平行四边形的判定，菱形的判定和性质，正方形的性质，判断出四边形ABCD是平行四边形是解本题的关键．19、（1）见解析；（2）S四边形ADOE =.【解析】
(1) 根据矩形的性质有OA=OB=OC=OD，根据四边形ADOE是平行四边形，得到OD∥AE，AE=OD. 等量代换得到AE=OB.即可证明四边形AOBE为平行四边形.根据有一组邻边相等的平行四边形是菱形即可证明.(2)根据菱形的性质有∠EAB=∠BAO.根据矩形的性质有AB∥CD，根据平行线的性质有∠BAC=∠ACD，求出∠DCA=60°，求出AD=.根据面积公式SΔADC，即可求解.【详解】（1）证明：∵矩形ABCD，∴OA=OB=OC=OD.∵平行四边形ADOE，∴OD∥AE，AE=OD. ∴AE=OB. ∴四边形AOBE为平行四边形. ∵OA=OB，∴四边形AOBE为菱形. （2）解：∵菱形AOBE，∴∠EAB=∠BAO. ∵矩形ABCD，∴AB∥CD. ∴∠BAC=∠ACD，∠ADC=90°. ∴∠EAB=∠BAO=∠DCA. ∵∠EAO+∠DCO=180°，∴∠DCA=60°. ∵DC=2，∴AD=. ∴SΔADC=. ∴S四边形ADOE =.【点睛】考查平行四边形的判定与性质，矩形的性质，菱形的判定与性质，解直角三角形，综合性比较强.20、（1）1；（2）．【解析】
（1）先计算乘方、绝对值、负整数指数幂和零指数幂，再计算乘法，最后计算加减运算可得；（2）先将分子、分母因式分解，再计算乘法，最后计算减法即可得．【详解】（1）原式=8-4+×6+1=8-4+2+1=1．（2）原式= ==．【点睛】本题主要考查实数和分式的混合运算，解题的关键是掌握绝对值性质、负整数指数幂、零指数幂及分式混合运算顺序和运算法则．21、这辆高铁列车全程运行的时间为1小时，平均速度为264千米/小时．【解析】
设动车组列车的平均速度为x千米/小时，则高铁列车的平均速度为（x+99）千米/小时，根据时间=路程÷速度结合高铁列车比动车组列车全程运行时间少3小时，即可得出关于x的分式方程，解之经检验后即可得出结论．【详解】设动车组列车的平均速度为x千米/小时，则高铁列车的平均速度为（x+99）千米/小时，根据题意得：﹣=3，解得：x1=161，x2=﹣264（不合题意，舍去），经检验，x=161是原方程的解，∴x+99=264，1320÷（x+99）=1．答：这辆高铁列车全程运行的时间为1小时，平均速度为264千米/小时．【点睛】本题考查了列分式方程解实际问题的运用及分式方程的解法的运用,解答时根据条件建立方程是关键,解答时对求出的根必须检验,这是解分式方程的必要步骤.22、见解析.【解析】
由“SAS”可证△ABC≌△DEC，可得BC＝CE，即可得结论．【详解】证明：∵AB＝DE，∠A＝∠D，∠ACB＝∠DCE＝90°∴△ABC≌△DEC（SAS）∴BC＝CE，∵AC＝AE+CE∴AC＝AE+BC【点睛】本题考查了全等三角形的判定和性质，熟练运用全等三角形的性质是本题的关键．23、（1）40;（2）想去D景点的人数是8，圆心角度数是72°;（3）280.【解析】
（1）用最想去A景点的人数除以它所占的百分比即可得到被调查的学生总人数；（2）先计算出最想去D景点的人数，再补全条形统计图，然后用360°乘以最想去D景点的人数所占的百分比即可得到扇形统计图中表示“醉美旅游景点D”的扇形圆心角的度数；（3）用800乘以样本中最想去B景点的人数所占的百分比即可．【详解】（1）被调查的学生总人数为8÷20%=40（人）；（2）最想去D景点的人数为40-8-14-4-6=8（人），补全条形统计图为：扇形统计图中表示“醉美旅游景点D”的扇形圆心角的度数为×360°=72°；（3）800×=280，所以估计“醉美旅游景点B“的学生人数为280人．【点睛】本题考查了条形统计图：条形统计图是用线段长度表示数据，根据数量的多少画成长短不同的矩形直条，然后按顺序把这些直条排列起来．从条形图可以很容易看出数据的大小，便于比较．也考查了扇形统计图和利用样本估计总体．24、 (1)见解析；(2) AC∥BD，理由见解析;(3)【解析】
（1）直接利用相似三角形的判定方法得出△BCE∽△DCP，进而得出答案；
（2）首先得出△PCE∽△DCB，进而求出∠ACB=∠CBD，即可得出AC与BD的位置关系；
（3）首先利用相似三角形的性质表示出BD，PM的长，进而根据三角形的面积公式得到△PBD的面积．【详解】（1）证明：∵△BCE和△CDP均为等腰直角三角形，∴∠ECB＝∠PCD＝45°，∠CEB＝∠CPD＝90°，∴△BCE∽△DCP，∴；（2）解：结论：AC∥BD，理由：∵∠PCE+∠ECD＝∠BCD+∠ECD＝45°，∴∠PCE＝∠BCD，又∵，∴△PCE∽△DCB，∴∠CBD＝∠CEP＝90°，∵∠ACB＝90°，∴∠ACB＝∠CBD，∴AC∥BD；（3）解：如图所示：作PM⊥BD于M，∵AC＝4，△ABC和△BEC均为等腰直角三角形，∴BE＝CE＝4，∵△PCE∽△DCB，∴，即，∴BD＝，∵∠PBM＝∠CBD﹣∠CBP＝45°，BP＝BE+PE＝4+1＝5，∴PM＝5sin45°＝∴△PBD的面积S＝BD•PM＝××＝．【点睛】本题考查相似三角形的性质和判定，解题的关键是掌握相似三角形的性质和判定.