高考数学统考一轮复习第7章立体几何第1节空间几何体的结构及其表面积体积学案

这是一份高考数学统考一轮复习第7章立体几何第1节空间几何体的结构及其表面积体积学案，共23页。

空间几何体的结构及其表面积、体积
[考试要求] 1.认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构.
2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图，能识别上述三视图所表示的立体模型，会用斜二测画法画出它们的直观图.
3.会用平行投影方法画出简单空间图形的三视图与直观图，了解空间图形的不同表示形式.
4.了解球、棱柱、棱锥、台体的表面积和体积的计算公式．
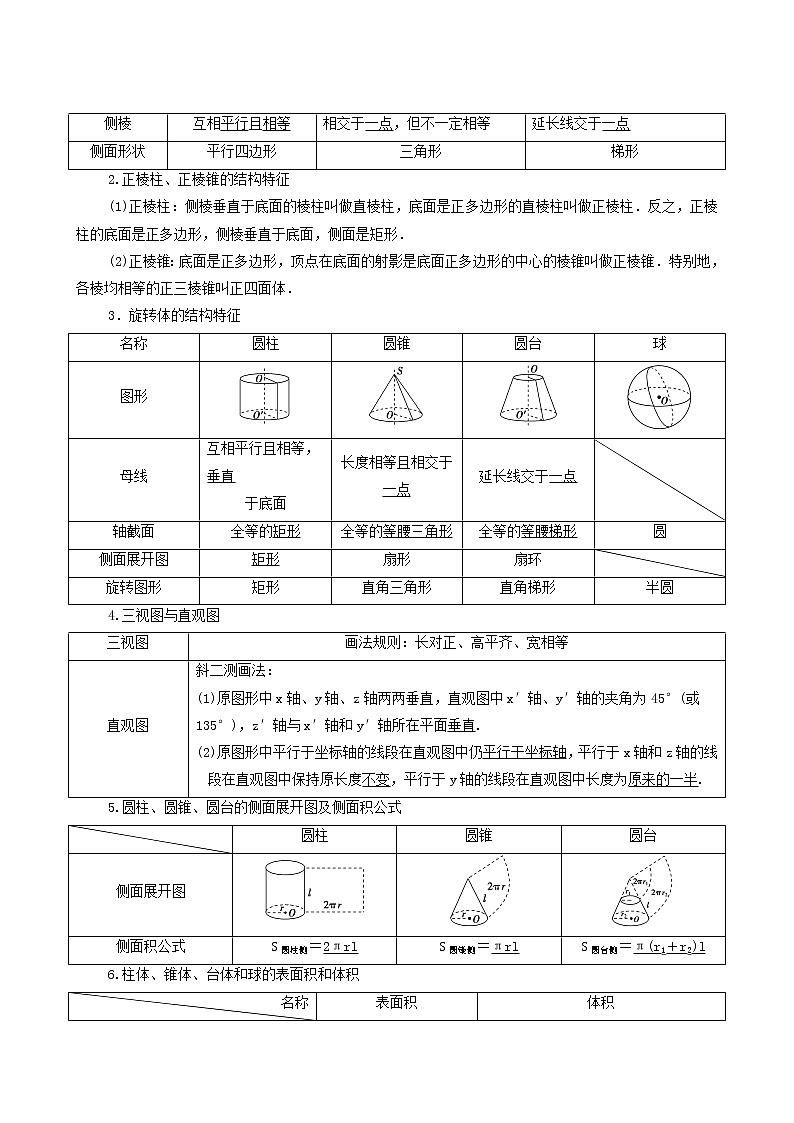
1．多面体的结构特征
2.正棱柱、正棱锥的结构特征
(1)正棱柱：侧棱垂直于底面的棱柱叫做直棱柱，底面是正多边形的直棱柱叫做正棱柱．反之，正棱柱的底面是正多边形，侧棱垂直于底面，侧面是矩形．
(2)正棱锥：底面是正多边形，顶点在底面的射影是底面正多边形的中心的棱锥叫做正棱锥．特别地，各棱均相等的正三棱锥叫正四面体．
3．旋转体的结构特征
4.三视图与直观图
5.圆柱、圆锥、圆台的侧面展开图及侧面积公式
6.柱体、锥体、台体和球的表面积和体积
eq \([常用结论])
1．按照斜二测画法得到的平面图形的直观图，其面积与原图形的面积的关系：
S直观图＝eq \f (\r(2),4)S原图形，S原图形＝2eq \r(2)S直观图．
2．多面体的内切球与外接球常用的结论
(1)设正方体的棱长为a，则它的内切球半径r＝eq \f (a,2)，外接球半径R＝eq \f (\r(3),2)a.
(2)设长方体的长、宽、高分别为a，b，c，则它的外接球半径R＝eq \f (\r(a2＋b2＋c2),2).
(3)设正四面体的棱长为a，则它的高为H＝eq \f (\r(6),3)a，内切球半径r＝eq \f (1,4)H＝eq \f (\r(6),12)a，外接球半径R＝eq \f (3,4)H＝eq \f (\r(6),4)a.
一、易错易误辨析(正确的打“√”，错误的打“×”)
(1)有两个面平行，其余各面都是平行四边形的几何体是棱柱．( )
(2)有一个面是多边形，其余各面都是三角形的几何体是棱锥．( )
(3)菱形的直观图仍是菱形．( )
(4)正方体、球、圆锥各自的三视图中，三视图均相同．( )
[答案] (1)× (2)× (3)× (4)×
二、教材习题衍生
1．如图所示，长方体ABCD­A′B′C′D′中被截去一部分，其中EH∥A′D′，则剩下的几何体是( )
A．棱台
B．四棱柱
C．五棱柱
D．简单组合体
C [由几何体的结构特征知，剩下的几何体为五棱柱．]
2．体积为8的正方体的顶点都在同一球面上，则该球的表面积为( )
A．12π B．eq \f (32,3)π C．8π D．4π
A [由题意可知正方体的棱长为2，其体对角线2eq \r(3)即为球的直径，所以球的表面积为4πR2＝(2R)2π＝12π，故选A．]
3．已知圆锥的表面积等于12π cm2，其侧面展开图是一个半圆，则底面圆的半径为( )
A．1 cm B．2 cm
C．3 cm D．eq \f (3,2) cm
B [S表＝πr2＋πrl＝πr2＋πr·2r＝3πr2＝12π，∴r2＝4，
∴r＝2(cm)．]
4．已知某几何体的三视图如图所示，则该几何体的体积为 ．
eq \f (16,3)π [由三视图可知，该几何体是一个圆柱挖去了一个同底等高的圆锥，其体积为π×22×2－eq \f (1,3)π×22×2＝eq \f (16,3)π.]
考点一 空间几何体的三视图、直观图和展开图
1.三视图画法的基本原则
长对正，高平齐，宽相等；画图时看不到的线画成虚线．
2．由三视图还原几何体的步骤
3．直观图画法的规则：斜二测画法．
4．通常利用空间几何体的表面展开图解决以下问题：(1)求几何体的表面积或侧面积；(2)求几何体表面上任意两个点的最短表面距离．
三视图
[典例1－1] (1)(2018·全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是( )
A B C D
(2)如图所示，在正方体ABCD­A1B1C1D1中，E为棱BB1的中点，过点A，E，C1的平面截去该正方体的上半部分，则剩余几何体的侧视图为( )
A B C D
(3)(2020·全国卷Ⅱ)如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M，在俯视图中对应的点为N，则该端点在侧视图中对应的点为( )
A．E B．F C．G D．H
(1)A (2)C (3)A [(1)由题意知，在咬合时带卯眼的木构件中，从俯视方向看，榫头看不见，所以是虚线，结合榫头的位置知选A．
(2)过点A，E，C1的截面如图所示，由图可知该剩余几何体的侧视图为C．
(3)由三视图知，该几何体是由两个长方体组合而成的，其直观图如图所示，由图知该端点在侧视图中对应的点为E，故选A．]
点评：画三视图时，可先找出各个顶点在投影面上的投影，然后再确定连线在投影面上的虚实．
直观图
[典例1－2] 已知正三角形ABC的边长为a，那么△ABC的平面直观图△A′B′C′的面积为( )
A．eq \f (\r(3),4)a2 B．eq \f (\r(3),8)a2 C．eq \f (\r(6),8)a2 D．eq \f (\r(6),16)a2
D [法一：如图①②所示的实际图形和直观图，
由图②可知，A′B′＝AB＝a，O′C′＝eq \f (1,2)OC＝eq \f (\r(3),4)a，
在图②中作C′D′⊥A′B′于D′，
则C′D′＝eq \f (\r(2),2)O′C′＝eq \f (\r(6),8)a，
所以S△A′B′C′＝eq \f (1,2)A′B′·C′D′＝eq \f (1,2)×a×eq \f (\r(6),8)a＝eq \f (\r(6),16)a2.
法二：S△ABC＝eq \f (1,2)×a×asin 60°＝eq \f (\r(3),4)a2，
又S直观图＝eq \f (\r(2),4)S原图＝eq \f (\r(2),4)×eq \f (\r(3),4)a2＝eq \f (\r(6),16)a2.故选D．]
点评：直观图的面积问题常常有两种解法：一是利用斜二测画法求解，注意 “斜”及“二测”的含义；二是直接套用等量关系：S直观图＝eq \f (\r(2),4)S原图形．
展开图
[典例1－3] 如图，在直三棱柱ABC­A1B1C1中，AB＝2，BC＝eq \r(3)，AC＝1，AA1＝3，F为棱AA1上的一动点，则当BF＋FC1最小时，△BFC1的面积为 ．
eq \f (\r(15),2) [将直三棱柱ABC­A1B1C1沿棱AA1展开成平面，连接BC1(图略)，与AA1的交点即为满足BF＋FC1最小时的点F，∵直三棱柱ABC­A1B1C1中，AB＝2，BC＝eq \r(3)，AC＝1，AA1＝3，再结合棱柱的性质，可得A1F＝eq \f (1,3)AA1＝1，故AF＝2.
由图形及棱柱的性质，可得BF＝eq \r(4＋4)＝2eq \r(2)，
FC1＝eq \r(1＋1)＝eq \r(2)，BC1＝eq \r(3＋9)＝2eq \r(3)，
cs∠BFC1＝eq \f (BF2＋FC\\al(2,1)－BC\\al(2,1),2×BF×FC1)＝eq \f (8＋2－12,2×2\r(2)×\r(2))＝－eq \f (1,4).
故sin∠BFC1＝eq \r(1－\f (1,16))＝eq \f (\r(15),4)，
∴△BFC1的面积为
S＝eq \f (1,2)×BF×FC1×sin∠BFC1
＝eq \f (1,2)×2eq \r(2)×eq \r(2)×eq \f (\r(15),4)＝eq \f (\r(15),2).]
点评：本题在探求BF＋FC1最小时，采用了化曲为直的策略，将空间问题平面化，在解决空间折线段最短问题时可适当考虑其展开图．
eq \([跟进训练])
1．(2018·全国卷Ⅰ)某圆柱的高为2，底面周长为16，其三视图如图所示．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为( )
A．2eq \r(17) B．2eq \r(5) C．3 D．2
B [先画出圆柱的直观图，根据题图的三视图可知点M，N的位置如图1所示．
图1 图2
圆柱的侧面展开图及M，N的位置(N为OP的四等分点)如图2所示，连接MN，则图中MN即为M到N的最短路径．ON＝eq \f (1,4)×16＝4，OM＝2，
∴MN＝eq \r(OM2＋ON2)＝eq \r(22＋42)＝2eq \r(5).
故选B．]
2．某几何体的正视图和侧视图如图①所示，它的俯视图的直观图是矩形O1A1B1C1，如图②，其中O1A1＝6，O1C1＝2，则该几何体的侧面积为( )
A．48 B．64 C．96 D．128
C [由题意可知俯视图的直观图面积为2×6＝12，
故俯视图的面积为24eq \r(2).
又由三视图可知该几何体为直四棱柱，且高为4，底面为边长为6的菱形．
所以几何体的侧面积为6×4×4＝96.故选C．]
考点二 空间几何体的表面积与体积
1.空间几何体表面积的求法
(1)旋转体的表面积问题注意其侧面展开图的应用．
(2)多面体的表面积是各个面的面积之和；组合体的表面积注意衔接部分的处理．
(3)以三视图为载体的需确定几何体中各元素之间的位置关系及数量．
2．空间几何体体积问题的常见类型及解题策略
(1)直接利用公式进行求解．
(2)用转换法、分割法、补形法等方法进行求解．
(3)以三视图的形式给出的应先得到几何体的直观图．

空间几何体的表面积
[典例2－1] (1)若某空间几何体的三视图如图所示，则该几何体的表面积是( )
A．48＋π B．48－π
C．48＋2π D．48－2π
(2)(2018·全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为( )
A．12eq \r(2)π B．12π C．8eq \r(2)π D．10π
(3)(2020·全国卷Ⅰ)已知A，B，C为球O的球面上的三个点，⊙O1为△ABC的外接圆．若⊙O1的面积为4π，AB＝BC＝AC＝OO1，则球O的表面积为( )
A．64π B．48π C．36π D．32π
(1)A (2)B (3)A [(1)该几何体是正四棱柱挖去了一个半球，正四棱柱的底面是正方形(边长为2)，高为5，半球的半径是1，那么该几何体的表面积为S＝2×2×2＋4×2×5－π×12＋2π×12＝48＋π，故选A．
(2)因为过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，所以圆柱的高为2eq \r(2)，底面圆的直径为2eq \r(2)，所以该圆柱的表面积为2×π×(eq \r(2))2＋2π×eq \r(2)×2eq \r(2)＝12π.
(3)如图所示，设球O的半径为R，⊙O1的半径为r，因为⊙O1的面积为4π，所以4π＝πr2，解得r＝2，又AB＝BC＝AC＝OO1，所以eq \f (AB,sin 60°)＝2r，解得AB＝2eq \r(3)，故OO1＝2eq \r(3)，所以R2＝OOeq \\al(2,1)＋r2＝(2eq \r(3))2＋22＝16，所以球O的表面积S＝4πR2＝64π.故选A．]
点评：解答本题T(1)时易误认为几何体的上底面不存在，导致计算错误．
空间几何体的体积
求空间几何体的体积的常用方法
[典例2－2] (1)如图所示，正三棱柱ABC­A1B1C1的底面边长为2，侧棱长为eq \r(3)，D为BC中点，则三棱锥A­B1DC1的体积为( )
A．3 B．eq \f (3,2)
C．1 D．eq \f (\r(3),2)
(2)(2017·全国卷Ⅱ)如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为( )
A．90π B．63π
C．42π D．36π
(3)已知正方体ABCD­A1B1C1D1的棱长为2，M、N分别为BB1、AB的中点，则三棱锥A­NMD1的体积为 ．
(1)C (2)B (3)eq \f (1,3) [(1)(直接法)如题图，在正三角形ABC中，D为BC中点，
则有AD＝eq \f (\r(3),2)AB＝eq \r(3)，
又∵平面BB1C1C⊥平面ABC，平面BB1C1C∩平面ABC＝BC，AD⊥BC，AD⊂平面ABC，由面面垂直的性质定理可得AD⊥平面BB1C1C，即AD为三棱锥A­B1DC1的底面B1DC1上的高，
(2)法一(分割法)：由题意知，该几何体是一个组合体，下半部分是一个底面半径为3，高为4的圆柱，其体积V1＝π×32×4＝36π.
上半部分是一个底面半径为3，高为6的圆柱的一半，
其体积V2＝eq \f (1,2)×π×32×6＝27π.
所以该组合体的体积V＝V1＋V2＝36π＋27π＝63π.
法二(补形法)：由题意知，该几何体是一圆柱被一平面截去一部分后所得的几何体，在该几何体上方再补上一个与其相同的几何体，让截面重合，则所得几何体为一个圆柱，故圆柱的底面半径为3，高为10＋4＝14，该圆柱的体积V1＝π×32×14＝126π.
故该几何体的体积为圆柱体积的一半，
即V＝eq \f (1,2)V1＝63π.
法三(估值法)：由题意，知eq \f (1,2)V圆柱＜V几何体＜V圆柱．又V圆柱＝π×32×10＝90π，所以45π＜V几何体＜90π.观察选项可知只有63π符合．
(3)(等体积法)如图，
∵正方体ABCD­A1B1C1D1的棱长为2，M、N分别为BB1、AB的中点，
∴S△ANM＝eq \f (1,2)×1×1＝eq \f (1,2)，
∴Veq \s\d5(A­NMD1)＝Veq \s\d5(D1­AMN)＝eq \f (1,3)×eq \f (1,2)×2＝eq \f (1,3).]
点评：处理体积问题的思路
(1)“转”：指的是转换底面与高，将原来不易求面积的底面转换为易求面积的底面，或将原来不易看出的高转换为易看出并易求解长度的高，即等体积法；
(2)“拆”：指的是将一个不规则的几何体拆成几个简单的几何体，便于计算，即分割法；
(3)“拼”：指的是将小几何体嵌入一个大几何体中，如将一个三棱锥复原成一个三棱柱，将一个三棱柱复原成一个四棱柱，这些都是拼补的方法，即补形法．
eq \([跟进训练])
1．(2019·浙江高考)祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V柱体＝Sh，其中S是柱体的底面积，h是柱体的高．若某柱体的三视图如图所示(单位：cm)，则该柱体的体积(单位：cm3)是( )
A．158 B．162
C．182 D．324
B [由三视图得该棱柱的高为6，底面可以看作是由两个直角梯形组合而成的，其中一个上底为4，下底为6，高为3，另一个的上底为2，下底为6，高为3，则该棱柱的体积为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f (2＋6,2)×3＋\f (4＋6,2)×3))×6＝162.故选B．]
2．若正四棱锥的底面边长和高都为2，则其表面积为 ．
4＋4eq \r(5) [如图．
由题意知底面正方形的边长为2，正四棱锥的高为2，
则正四棱锥的斜高PE＝eq \r(22＋12)＝eq \r(5).
所以该四棱锥的侧面积S＝4×eq \f (1,2)×2×eq \r(5)＝4eq \r(5)，
∴S表＝2×2＋4eq \r(5)＝4＋4eq \r(5).]
考点三 与球有关的切、接问题
与球有关的切、接问题的解法
(1)旋转体的外接球：常用的解题方法是过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．
(2)多面体的外接球：常用的解题方法是将多面体还原到正方体和长方体中再去求解．
①若球面上四点P，A，B，C中PA，PB，PC两两垂直或三棱锥的三条侧棱两两垂直，可构造长方体或正方体，利用2R＝eq \r(a2＋b2＋c2)求R.
②一条侧棱垂直底面的三棱锥问题：可补形成直三棱柱．先借助几何体的几何特征确定球心位置，然后把半径放在直角三角形中求解．

[典例3] (1)(2020·全国卷Ⅲ)已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为 ．
(2)(2020·福建十校联考)已知三棱锥P­ABC的三条侧棱两两互相垂直，且AB＝eq \r(5)，BC＝eq \r(7)，AC＝2，则此三棱锥的外接球的体积为( )
A．eq \f (8,3)π B．eq \f (8\r(2),3)π C．eq \f (16,3)π D．eq \f (32,3)π
(3)已知直三棱柱ABC­A1B1C1的各顶点都在以O为球心的球面上，且∠BAC＝eq \f (3π,4)，AA1＝BC＝2，则球O的体积为( )
A．4eq \r(3)π B．8π C．12π D．20π
(1)eq \f (\r(2),3)π (2)B (3)A [(1)易知半径最大的球即为该圆锥的内切球．圆锥PE及其内切球O如图所示，设内切球的半径为R，则sin∠BPE＝eq \f (R,OP)＝eq \f (BE,PB)＝eq \f (1,3)，所以OP＝3R，所以PE＝4R＝eq \r(PB2－BE2)＝eq \r(32－12)＝2eq \r(2)，所以R＝eq \f (\r(2),2)，所以内切球的体积V＝eq \f (4,3)πR3＝eq \f (\r(2),3)π，即该圆锥内半径最大的球的体积为eq \f (\r(2),3)π.
(2)∵AB＝eq \r(5)，BC＝eq \r(7)，AC＝2，∴PA＝1，PC＝eq \r(3)，PB＝2.以PA，PB，PC为过同一顶点的三条棱，作长方体如图所示，
则长方体的外接球同时也是三棱锥P­ABC的外接球．
∵长方体的体对角线长为eq \r(1＋3＋4)＝2eq \r(2)，
∴球的直径为2eq \r(2)，半径R＝eq \r(2)，
因此，三棱锥P­ABC外接球的体积是eq \f (4,3)πR3＝eq \f (4,3)π×(eq \r(2))3＝eq \f (8\r(2),3)π.故选B．
(3)在底面△ABC中，由正弦定理得底面△ABC所在的截面圆的半径为r＝eq \f (BC,2sin∠BAC)＝eq \f (2,2sin \f (3π,4))＝eq \r(2)，
则直三棱柱ABC­A1B1C1的外接球的半径为R＝eq \r(r2＋\b\lc\(\rc\)(\a\vs4\al\c1(\f (AA1,2)))eq \s\up12(2))＝eq \r(\r(2)2＋12)＝eq \r(3)，
则直三棱柱ABC­A1B1C1的外接球的体积为eq \f (4,3)πR3＝4eq \r(3)π.故选A．]
[母题变迁]
1．若将本例(3)的条件“∠BAC＝eq \f (3π,4)，AA1＝BC＝2”换为“AB＝3，AC＝4，AB⊥AC，AA1＝12”，则球O的半径为 ．
eq \f (13,2) [如图所示，过球心作平面ABC的垂线，则垂足为BC的中点M.
又AM＝eq \f (1,2)BC＝eq \f (5,2)，OM＝eq \f (1,2)AA1＝6，
所以球O的半径
R＝OA＝ eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(\f (5,2)))eq \s\up12(2)＋62)＝eq \f (13,2).]
2．若将本例(3)的条件改为“正四面体的各顶点都在以O为球心的球面上”，则此正四面体的表面积S1与其内切球的表面积S2的比值为 ．
eq \f (6\r(3),π) [设正四面体棱长为a，则正四面体表面积为S1＝4×eq \f (\r(3),4)·a2＝eq \r(3)a2，其内切球半径r为正四面体高的eq \f (1,4)，
即r＝eq \f (1,4)·eq \f (\r(6),3)a＝eq \f (\r(6),12)a，因此内切球表面积为S2＝4πr2＝eq \f (πa2,6)，
则eq \f (S1,S2)＝eq \f (\r(3)a2,\f (πa2,6))＝eq \f (6\r(3),π).]
3．若将本例(3)的条件改为“侧棱和底面边长都是3eq \r(2)的正四棱锥的各顶点都在以O为球心的球面上”，则其外接球的半径为 ．
3 [依题意，得该正四棱锥底面对角线的长为3eq \r(2)×eq \r(2)＝6，高为eq \r(3\r(2)eq \s\up12(2)－\b\lc\(\rc\)(\a\vs4\al\c1(\f (1,2)×6))eq \s\up12(2))＝3，
因此底面中心到各顶点的距离均等于3，所以该正四棱锥的外接球的球心即为底面正方形的中心，其外接球的半径为3.]
点评：通过本例(3)及母题变迁训练，我们可以看出构造法、补形法等是处理“外接”问题的主要方法，其关键是找到球心，借助勾股定理求球的半径．
(1)锥体的外接球问题，解决这类问题的关键是抓住外接球的特点，即球心到各个顶点的距离等于球的半径．
(2)柱体的外接球问题，其解题关键在于确定球心在多面体中的位置，找到球的半径或直径与多面体相关元素之间的关系，结合原有多面体的特性求出球的半径，然后再利用球的表面积和体积公式进行正确计算．
eq \([跟进训练])
1．(2018·全国卷Ⅲ)设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且其面积为9eq \r(3)，则三棱锥D­ABC体积的最大值为( )
A．12eq \r(3) B．18eq \r(3) C．24eq \r(3) D．54eq \r(3)
B [由等边△ABC的面积为9eq \r(3)，
可得eq \f (\r(3),4)AB2＝9eq \r(3)，所以AB＝6，
所以等边△ABC的外接圆的半径为r＝eq \f (\r(3),3)AB＝2eq \r(3).
设球的半径为R，球心到等边△ABC的外接圆圆心的距离为d，则d＝eq \r(R2－r2)＝eq \r(16－12)＝2.
所以三棱锥D­ABC高的最大值为2＋4＝6，
所以三棱锥D­ABC体积的最大值为eq \f (1,3)×9eq \r(3)×6＝18eq \r(3).]
2．(2020·南宁模拟)已知三棱锥P­ABC中，△ABC为等边三角形，PA＝PB＝PC＝3，PA⊥PB，则三棱锥P­ABC的外接球的体积为( )
A．eq \f (27π,2) B．eq \f (27\r(3)π,2) C．27eq \r(3)π D．27π
B [∵三棱锥P­ABC中，△ABC为等边三角形，PA＝PB＝PC＝3，
∴△PAB≌△PBC≌△PAC．
∵PA⊥PB，∴PA⊥PC，PC⊥PB．
以PA，PB，PC为过同一顶点的三条棱作正方体(如图所示)，则正方体的外接球同时也是三棱锥P­ABC的外接球．
∵正方体的体对角线长为eq \r(32＋32＋32)＝3eq \r(3)，∴其外接球半径R＝eq \f (3\r(3),2).因此三棱锥P­ABC的外接球的体积V＝eq \f (4π,3)×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f (3\r(3),2)))eq \s\up12(3)＝eq \f (27\r(3)π,2).]
eq \([素养案例1]) 已知边长为2的等边三角形ABC，D为BC的中点，沿AD进行折叠，使折叠后的∠BDC＝eq \f (π,2)，则过A，B，C，D四点的球的表面积为( )
A．3π B．4π C．5π D．6π
C [连接BC(图略)，由题知几何体ABCD为三棱锥，BD＝CD＝1，AD＝eq \r(3)，BD⊥AD，CD⊥AD，BD⊥CD，将折叠后的图形补成一个长、宽、高分别是eq \r(3)，1,1的长方体，其体对角线长为eq \r(1＋1＋3)＝eq \r(5)，故该三棱锥外接球的半径是eq \f (\r(5),2)，其表面积为5π.]
[评析] 若几何体存在三条两两垂直的线段或者三条线有两条垂直，可构造墙角模型(如下图)，直接用公式(2R)2＝a2＋b2＋c2求出R.
eq \([素养培优])
(2020·河北重点中学6月联考)阿基米德是伟大的古希腊数学家，他和高斯、牛顿并称为世界三大数学家．他的一个重要数学成就是“圆柱容球”定理，即在带盖子的圆柱形容器(容器的厚度忽略不计)里放一个球，该球与圆柱形容器的两个底面和侧面都相切，则球的体积是圆柱形容器的容积的eq \f (2,3)，并且球的表面积也是圆柱形容器的表面积的eq \f (2,3).则该圆柱形容器的容积与它的外接球的体积之比为( )
A．eq \f (3\r(2),8) B．eq \f (\r(2),4) C．eq \f (2,3) D．eq \f (\r(2),3)
A [设容器里所放球的半径为R，则圆柱形容器的底面半径为R，设圆柱形容器的高为h，
由题意知h＝2R，圆柱形容器的外接球的半径为eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(\f (2R,2)))eq \s\up12(2)＋R2)＝eq \r(2)R.
圆柱形容器的容积V＝πR2·2R＝2πR3，
V外接球＝eq \f (4,3)π(eq \r(2)R)3＝eq \f (8\r(2),3)πR3，
所以eq \f (V,V外接球)＝eq \f (2πR3,\f (8\r(2),3)πR3)＝eq \f (3\r(2),8)，故选A．]
eq \([素养案例2]) 三棱锥S­ABC中，SA＝BC＝eq \r(13)，SB＝AC＝eq \r(5)，SC＝AB＝eq \r(10).则三棱锥的外接球的表面积为 ．
14π [如图，在长方体中，设AE＝a，BE＝b，CE＝c.
则SC＝AB＝eq \r(a2＋b2)＝eq \r(10)，
SA＝BC＝eq \r(b2＋c2)＝eq \r(13)，
SB＝AC＝eq \r(a2＋c2)＝eq \r(5).
从而a2＋b2＋c2＝14＝(2R)2，可得S＝4πR2＝14π.故所求三棱锥的外接球的表面积为14π.]
[评析] 三棱锥的相对棱相等，探寻球心无从着手，注意到长方体的相对面的面对角线相等，可在长方体中构造三棱锥，从而巧妙探索外接球半径．
eq \([素养培优])
(2019·全国卷Ⅰ)已知三棱锥P­ABC的四个顶点在球O的球面上，PA＝PB＝PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF＝90°， 则球O的体积为( )
A．8eq \r(6)π B．4eq \r(6)π C．2eq \r(6)π D．eq \r(6)π
D [因为点E，F分别为PA，AB的中点，所以EF∥PB，
因为∠CEF＝90°，所以EF⊥CE，所以PB⊥CE.
取AC的中点D，连接BD，PD，易证AC⊥平面BDP，
所以PB⊥AC，又AC∩CE＝C，AC，CE⊂平面PAC，所以PB⊥平面PAC，
所以PB⊥PA，PB⊥PC，因为PA＝PB＝PC，△ABC为正三角形，
所以PA⊥PC，即PA，PB，PC两两垂直，将三棱锥P­ABC放在正方体中．因为AB＝2，所以该正方体的棱长为eq \r(2)，所以该正方体的体对角线长为eq \r(6)，所以三棱锥P­ABC的外接球的半径R＝eq \f (\r(6),2)，所以球O的体积V＝eq \f (4,3)πR3＝eq \f (4,3)πeq \b\lc\(\rc\)(\a\vs4\al\c1(\f (\r(6),2)))eq \s\up12(3)＝eq \r(6)π，故选D．]
eq \([素养案例3]) 平面四边形ABCD中，AB＝AD＝CD＝1，BD＝eq \r(2)，BD⊥CD．将其沿对角线BD折成四面体A′BCD，使平面A′BD⊥平面BCD．若四面体A′BCD的顶点在同一球面上，则该球的体积为( )
A．eq \f (\r(3),2)π B．3π C．eq \f (\r(2),3)π D．2π
A [如图，设BD，BC的中点分别为E，F.因点F为底面直角△BCD的外心，知三棱锥A′­BCD的外接球球心必在过点F且与平面BCD垂直的直线l1上．又点E为底面直角△A′BD的外心，知外接球球心必在过点E且与平面A′BD垂直的直线l2上．因而球心为l1与l2的交点．又FE∥CD，CD⊥BD知FE⊥平面A′BD．从而可知球心为点F.又A′B＝A′D＝1，CD＝1知BD＝eq \r(2)，球半径R＝FD＝eq \f (BC,2)＝eq \f (\r(3),2).故V＝eq \f (4,3)πeq \b\lc\(\rc\)(\a\vs4\al\c1(\f (\r(3),2)))eq \s\up12(3)＝eq \f (\r(3),2)π.]
[评析] 三棱锥侧面与底面垂直时，可紧扣球心与底面三角形外心连线垂直于底面这一性质，利用底面与侧面的外心，巧探外接球球心，妙求半径．
eq \([素养培优])
(2020·广州模拟)三棱锥P­ABC中，平面PAC⊥平面ABC，AB⊥AC，PA＝PC＝AC＝2，AB＝4，则三棱锥P­ABC的外接球的表面积为( )
A．23π B．eq \f (23,4)π C．64π D．eq \f (64,3)π
D [如图，设O′为正△PAC的中心，D为Rt△ABC斜边的中点，H为AC中点．由平面PAC⊥平面ABC．则O′H⊥平面ABC．作O′O∥HD，OD∥O′H，则交点O为三棱锥外接球的球心，连接OP，又O′P＝eq \f (2,3)PH＝eq \f (2,3)×eq \f (\r(3),2)×2＝eq \f (2\r(3),3)，OO′＝DH＝eq \f (1,2)AB＝2.∴R2＝OP2＝O′P2＋O′O2＝eq \f (4,3)＋4＝eq \f (16,3).
故几何体外接球的表面积S＝4πR2＝eq \f (64,3)π.]
eq \([素养案例4]) 一个正六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为eq \f (9,8)，底面周长为3，则这个球的体积为 ．
eq \f (4π,3) [设正六棱柱底面边长为a，正六棱柱的高为h，底面外接圆的半径为r，则a＝eq \f (1,2)，底面积为S＝6·eq \f (\r(3),4)·eq \b\lc\(\rc\)(\a\vs4\al\c1(\f (1,2)))eq \s\up12(2)＝eq \f (3\r(3),8)，V柱＝Sh＝eq \f (3\r(3),8)h＝eq \f (9,8)，∴h＝eq \r(3)，R2＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f (\r(3),2)))eq \s\up12(2)＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f (1,2)))eq \s\up12(2)＝1，R＝1，球的体积为V＝eq \f (4π,3).]
[评析] 直棱柱的外接球、圆柱的外接球模型如图：
其外接球球心就是上下底面外接圆圆心连线的中点．
eq \([素养培优])
(2017·全国卷Ⅲ)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )
A．π B．eq \f (3π,4) C．eq \f (π,2) D．eq \f (π,4)
B [设圆柱的底面半径为r，球的半径为R，且R＝1，由圆柱两个底面的圆周在同一个球的球面上可知，r，R及圆柱的高的一半构成直角三角形．
∴r＝eq \r(1－\b\lc\(\rc\)(\a\vs4\al\c1(\f (1,2)))eq \s\up12(2))＝eq \f (\r(3),2).
∴圆柱的体积为V＝πr2h＝eq \f (3,4)π×1＝eq \f (3π,4).
故选B．]
(1)题设：如图①，三棱锥P­ABC是正三棱锥，求其内切球的半径．
图①
第一步：先画出内切球的截面图，E，H分别是两个三角形的外心；
第二步：求DH＝eq \f (1,3)CD，PO＝PH－r，PD是侧面△ABP的高；
第三步：由△POE∽△PDH，建立等式：eq \f (OE,DH)＝eq \f (PO,PD)，解出r.
(2)题设：如图②，四棱锥P­ABCD是正四棱锥，求其内切球的半径．
图②
第一步：先画出内切球的截面图，P，O，H三点共线；
第二步：求FH＝eq \f (1,2)BC，PO＝PH－r，PF是侧面△PCD的高；
第三步：由△POG∽△PFH，建立等式：eq \f (OG,HF)＝eq \f (PO,PF)，解出r.
(3)题设：三棱锥P­ABC是任意三棱锥，求其内切球半径．
方法：等体积法，三棱锥P­ABC体积等于内切球球心与四个面构成的四个三棱锥的体积之和；
第一步：先求出四个表面的面积和整个锥体体积；
第二步：设内切球的半径为r，球心为O，建立等式：VP­ABC＝VO­ABC＋VO­PAB＋VO­PAC＋VO­PBC⇒VP­ABC
＝eq \f (1,3)S△ABC·r＋eq \f (1,3)S△PAB·r＋eq \f (1,3)S△PAC·r＋eq \f (1,3)S△PBC·r＝eq \f (1,3)(S△ABC＋S△PAB＋S△PAC＋S△PBC)·r；
第三步：解出r＝eq \f (3VP­ABC,S△ABC＋S△PAB＋S△PAC＋S△PBC).
eq \([素养案例5]) (1)将半径为3，圆心角为eq \f (2π,3)的扇形围成一个圆锥，则该圆锥的内切球的表面积为( )
A．π B．2π C．3π D．4π
(2)如图，在四棱锥P­ABCD中，底面ABCD是边长为m的正方形，PD⊥底面ABCD，且PD＝m，PA＝PC＝eq \r(2)m，若在这个四棱锥内放一个球，则此球的最大半径是 ．
(1)B (2)eq \f (1,2)(2－eq \r(2))m [(1)半径为3，圆心角为eq \f (2π,3)的扇形弧长为2π，
故其围成的圆锥母线长为3，底面圆周长为2π，
得其底面半径为1，如图，MB＝1，AB＝3, ∴AM＝2eq \r(2)，由相似可得eq \f (ON,MB)＝eq \f (AO,AB)，得ON＝eq \f (\r(2),2)，
∴S球＝4π×eq \f (1,2)＝2π.故选B．
(2)由PD⊥底面ABCD得PD⊥AD．又PD＝m，PA＝eq \r(2)m，则AD＝m.设内切球的球心为O，半径为R，连接OA，OB，OC，OD，OP(图略)，易知VP­ABCD＝VO­ABCD＋VO­PAD＋VO­PAB＋VO­PBC＋VO­PCD，即eq \f (1,3)·m2·m＝eq \f (1,3)m2R＋eq \f (1,3)×eq \f (1,2)m2R＋eq \f (1,3)×eq \f (1,2)×eq \r(2)m2·R＋eq \f (1,3)×eq \f (1,2)×eq \r(2)m2·R＋eq \f (1,3)×eq \f (1,2)m2R，解得R＝eq \f (1,2)(2－eq \r(2))m，所以此球的最大半径是eq \f (1,2)(2－eq \r(2))m.]
[评析] 结合本题(2)的条件，采用体积分割法求解本题，即利用体积相等建立等量关系．
eq \([素养培优])
有一个倒圆锥形容器，它的轴截面是顶角的余弦值为eq \f (1,2)的等腰三角形．在容器内放一个半径为r的铁球，并注水，使水面与球正好相切，然后将球取出，则这时容器中水的深度为 ．
eq \r(3,15)r [如图，作出轴截面，因为轴截面是顶角的余弦值为eq \f (1,2)的等腰三角形，所以顶角为eq \f (π,3)，所以该轴截面为正三角形．根据切线性质知当球在容器内时，水的深度为3r，水面所在圆的半径为eq \r(3)r，则容器内水的体积V＝eq \f (1,3)π(eq \r(3)r)2·3r－eq \f (4,3)πr3＝eq \f (5,3)πr3.将球取出后，设容器中水的深度为h，则水面圆的半径为eq \f (\r(3),3)h，从而容器内水的体积V′＝eq \f (1,3)πeq \b\lc\(\rc\)(\a\vs4\al\c1(\f (\r(3),3)h))eq \s\up12(2)h＝eq \f (1,9)πh3，由V＝V′，得h＝eq \r(3,15)r，所以这时容器中水的深度为eq \r(3,15)r.]
eq \([素养案例6]) (2016·全国卷Ⅲ)在封闭的直三棱柱ABC­A1B1C1内有一个体积为V的球．若AB⊥BC，AB＝6，BC＝8，AA1＝3，则V的最大值是( )
A．4π B．eq \f (9π,2) C．6π D．eq \f (32π,3)
B [由题意得要使球的体积最大，则球与直三棱柱的若干面相切．设球的半径为R，∵△ABC的内切圆半径为eq \f (6＋8－10,2)＝2，∴R≤2.
又2R≤3，
∴R≤eq \f (3,2)，∴Vmax＝eq \f (4,3)πeq \b\lc\(\rc\)(\a\vs4\al\c1(\f (3,2)))eq \s\up12(3)＝eq \f (9,2)π.故选B．]
[评析] 解答本题的关键是当V取得最大值时，球与上下底面还是与侧面相切的问题．
eq \([素养培优])
体积为eq \f (4π,3)的球与正三棱柱的所有面均相切，则该棱柱的体积为 ．
6eq \r(3) [设球的半径为R，由eq \f (4π,3)R3＝eq \f (4π,3)，得R＝1，所以正三棱柱的高h＝2.
设底面边长为a，
则eq \f (1,3)×eq \f (\r(3),2)a＝1，所以a＝2eq \r(3).
所以V＝eq \f (\r(3),4)×(2eq \r(3))2×2＝6eq \r(3).]
全国卷五年考情图解
高考命题规律把握
1.考查形式
高考在本章一般命制2道小题、1道解答题，分值约占22分.
2.考查内容
(1)小题主要考查三视图、几何体体积与表面积计算，此类问题属于中档题目；对于球与棱柱、棱锥的切接问题，知识点较整合，难度稍大.
(2)解答题一般位于第18题或第19题的位置，常设计两问：第(1)问重点考查线面位置关系的证明；第(2)问重点考查空间角，尤其是二面角、线面角的计算．属于中档题目.
名称
棱柱
棱锥
棱台
图形
底面
互相平行且全等
多边形
互相平行且相似
侧棱
互相平行且相等
相交于一点，但不一定相等
延长线交于一点
侧面形状
平行四边形
三角形
梯形
名称
圆柱
圆锥
圆台
球
图形
母线
互相平行且相等，垂直
于底面
长度相等且相交于一点
延长线交于一点
轴截面
全等的矩形
全等的等腰三角形
全等的等腰梯形
圆
侧面展开图
矩形
扇形
扇环
旋转图形
矩形
直角三角形
直角梯形
半圆
三视图
画法规则：长对正、高平齐、宽相等
直观图
斜二测画法：
(1)原图形中x轴、y轴、z轴两两垂直，直观图中x′轴、y′轴的夹角为45°(或135°)，z′轴与x′轴和y′轴所在平面垂直.
(2)原图形中平行于坐标轴的线段在直观图中仍平行于坐标轴，平行于x轴和z轴的线段在直观图中保持原长度不变，平行于y轴的线段在直观图中长度为原来的一半.
圆柱
圆锥
圆台
侧面展开图
侧面积公式
S圆柱侧＝2πrl
S圆锥侧＝πrl
S圆台侧＝π(r1＋r2)l
名称
几何体
表面积
体积
柱体(棱柱和圆柱)
S表面积＝S侧＋2S底
V＝S底h
锥体(棱锥和圆锥)
S表面积＝S侧＋S底
V＝eq \f (1,3)S底h
台体(棱台和圆台)
S表面积＝S侧＋S上＋S下
V＝eq \f (1,3)(S上＋S下＋eq \r(S上S下))h
球
S＝4πR2
V＝eq \f (4,3)πR3
核心素养5 用数学眼光观察世界——巧解简单几何体的外接球与内切球问题
简单几何体外接球与内切球问题是立体几何中的难点，也是历年高考重要的考点，几乎每年都要考查，重在考查考生的直观想象能力和逻辑推理能力．此类问题实质是解决球的半径长或确定球心O的位置问题，其中球心的确定是关键．
下面从六个方面分类阐述该类问题的求解策略.
利用长方体的体对角线探索外接球半径
利用长方体的面对角线探索外接球半径
利用底面三角形与侧面三角形的外心探索球心
利用直棱柱上下底面外接圆圆心的连线确定球心
锥体的内切球问题
柱体的内切球问题