专题05 三角形-暑假初三升高一数学衔接知识自学讲义（人教A版2019）

专题05 三角形

【知识点梳理】

知识点1：三角形的“四心”

三角形是最重要的基本平面图形，很多较复杂的图形问题可以化归为三角形的问题.

如图3.2-1 ，在三角形中，有三条边，三个角，三个顶点，在三角形中，角平分线、中线、高（如图3.2-2）是三角形中的三种重要线段.      

三角形的三条中线相交于一点，这个交点称为三角形的重心.三角形的重心在三角形的内部，恰好是每条中线的三等分点.

三角形的三条角平分线相交于一点，是三角形的内心. 三角形的内心在三角形的内部，它到三角形的三边的距离相等.

三角形的三条高所在直线相交于一点，该点称为三角形的垂心.锐角三角形的垂心一定在三角形的内部，直角三角形的垂心为他的直角顶点，钝角三角形的垂心在三角形的外部.

过不共线的三点A、B、C有且只有一个圆，该圆是三角形ABC的外接圆，圆心O为三角形的外心.三角形的外心到三个顶点的距离相等，是各边的垂直平分线的交点.

知识点2：几种特殊的三角形

结论一：等腰三角形底边上三线（角平分线、中线、高线）合一.因而在等腰三角形ABC中，三角形的内心I、重心G、垂心H必然在一条直线上.

结论二：正三角形三条边长相等，三个角相等，且四心（内心、重心、垂心、外心）合一，该点称为正三角形的中心.

【题型归纳目录】

题型1：三角形的“四心”

题型2：几种特殊的三角形

【典型例题】

题型1：三角形的“四心”

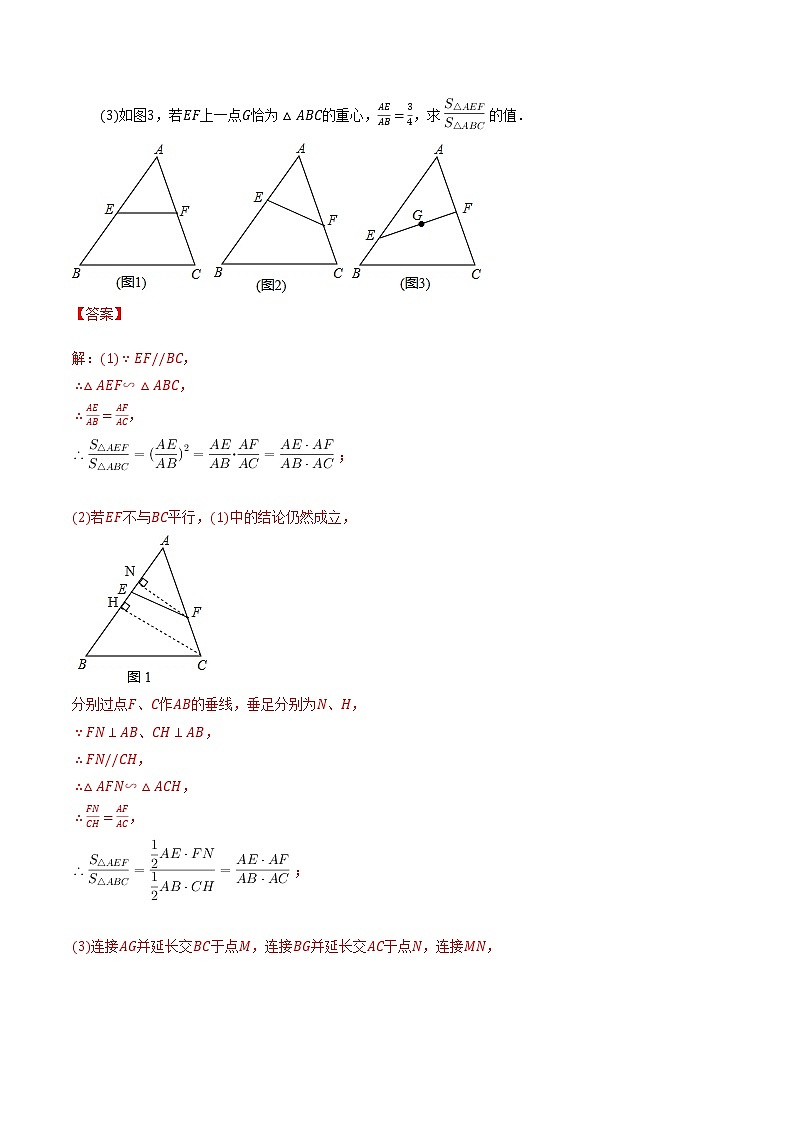
例1.在中，、分别为线段、上的点不与、、重合．
如图，若，求证：
如图，若不与平行，中的结论是否仍然成立？请说明理由；
如图，若上一点恰为的重心，，求的值．

例2.已知反比例函数的图象与正比例函数的图象交于，两点，且点在第二象限，点的横坐标为过点作轴，垂足为，的面积为．

求这两个函数的表达式．

若是这个反比例函数图象上的点，且的面积是，求点的坐标．

例3.三角形三条边上的中线交于一点，这个点叫三角形的重心．如图是的重心．求证：．

 

例4.如图，在中，以为直径作交于，平分交于，若．
 

求证：是的切线．

若，，求的长．

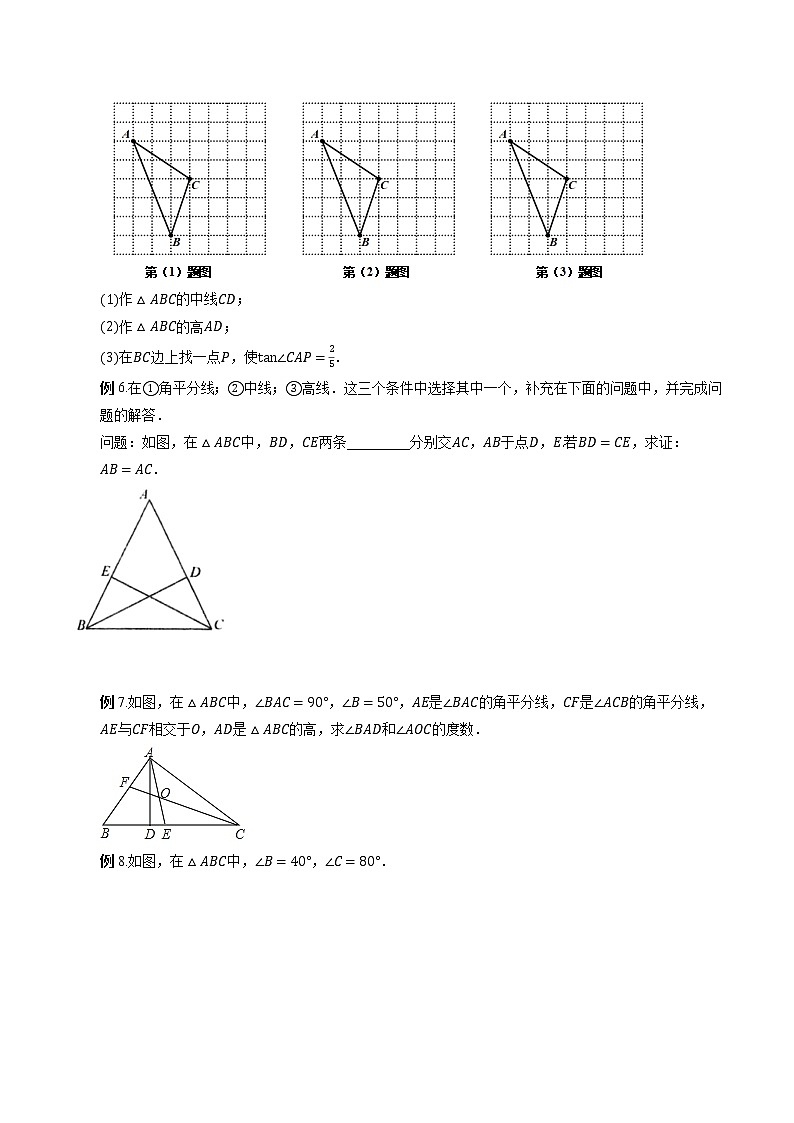
例5.如图是由边长为的小正方形构成的网格，每个小正方形的顶点叫做格点．的顶点在格点上．仅用无刻度尺的直尺在给定网格中画图，画图过程用虚线表示，画图结果用实线表示，按步骤完成下列问题：

作的中线；     

作的高；

在边上找一点，使．

例6.在角平分线；中线；高线．这三个条件中选择其中一个，补充在下面的问题中，并完成问题的解答．

问题：如图，在中，，两条_________分别交，于点，若，求证：．

例7.如图，在中，，，是的角平分线，是的角平分线，与相交于，是的高，求和的度数．

例8.如图，在中，，．
 

求的度数；

平分交于点，于点，求的度数．

题型2：几种特殊的三角形

例9.如图，在中，，点是的中点，点是上一点，以点为圆心、为半径作，与相交于点，与相切于点，连接与相交于点．
求证：平；
当，时，求的长．

例10.如图，已知正方形的边长为，点在边上，点在的延长线上，设正方形的面积为，以线段和为邻边的矩形的面积为，且．

求线段的长．

若为边上一点，，连接，，判断的形状．

例11.如图，在和中，，，与相交于点．

求证：≌；

是何种三角形？证明你的结论．

例12.据图回答问题
 
【背景阅读】在长方形纸片中，有两组对边分别平行和相等，如图，长方形纸片中，有且，且在折叠长方形纸片时，翻折前后的图形应是全等的图形．
【实践操作】如图，长方形的纸片中，，，把该纸片沿直线折叠，点落在点处，交于点．

图中有等腰三角形吗？说明理由．

求重叠部分即的面积．

【问题解决】如图，长方形纸片中，，，点在边上，将纸片沿折叠，点落在点处，，分别交于点，，且，求的长．

例13.如图，设和都是等边三角形，并且．
求证：≌；
求的度数．



 

例14.如图，在中，与的角平分线，相交于点，延长交的外接圆于点，连结，，，且．

求证：是等边三角形．

若，猜想是何种特殊四边形，并证明你的猜想．

例15.如图，是等边内一点，连接、、，且，，，将绕点顺时针旋转后得到，连接．

求：旋转角的度数____；

线段的长____；

求的度数．

如图所示，是等腰直角内一点，连接、、，将绕点顺时针旋转后得到，连接当、、满足什么条件时，？请给出证明．

例16.如图，菱形的对角线、相交于点，过点作且，连接、，连接交于点．

求证：
若菱形的边长为，求的长．

【过关测试】

一、选择题（本大题共10小题，共30.0分）

1.如图，在平行四边形中，，是的中点，作，垂足在线段上，连接、，则以下结论：
；；；，
一定成立的是

A.  B.  C.  D.

2.如图，中，，，分别以点和点为圆心，大于的长为半径作弧，两弧相交于、两点，作直线，交于点，连接，则的度数是

A.  B.  C.  D.

3.如图，在四边形中，，，，，若，则的大小为

A.  B.  C.  D.

4.如图，是的角平分线，，分别是和的高，得到下列四个结论：；；当时，四边形是正方形；其中正确的是

A.
B.
C.
D.

5.如图，在中，为斜边的中线，过点作于点，延长至点，使，连接，，点在线段上，连接，且，，下列结论：
；
四边形是平行四边形；
；
．
其中正确结论的个数是

A. 个 B. 个 C. 个 D. 个

6.如图，在中，，，于点，于点，若，，则的长度是

A.
B.
C.
D.

7.如图，正方形中，，相交于点，是的中点．动点从点出发，沿着的路径以每秒个单位长度的速度运动到点，在此过程中线段的长度随着运动时间的函数关系如图所示，则的长为

A.  B.  C.  D.

8.如图，在中，点，分别是边，的中点，点是线段上的一点．连接，，，且，，则的长是

A.
B.
C.
D.

9.如图，已知，添加以下条件，不能使≌的是

A.  B.
C.  D.

10.如图所示，点是矩形对角线的中点，交于点若，，则的长为

A.
B.
C.
D.

二、填空题（本大题共10小题，共30.0分）

11.如图，是一张顶角为的三角形纸片，，，现将折叠，使点与点重合，折痕为，则的长为______．

12.如图，为的中位线，点在上，且，若，，则的长为______．

13.如图，在中，和的平分线相交于点，过点作交于，交于，过点作于，下列四个结论：
；
；
点到各边的距离相等；
设，，则．
其中正确的结论是______填序号

14.如图，矩形中，点，分别在边，上，连接，，，将和分别沿，折叠，使点，恰好落在上的同一点，记为点若，，则______．

15.如图，在中，，于点，，，则______．
 

16.对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形，对角线、交于点若，，则______．

 

17.如图，在中，的半径为，点是边上的动点，过点作的一条切线点为切点，则线段长的最小值为______．

 

18.如图，已知两块三角板如图摆放，点和点分别在两块三角板的边上，一块三角板的顶点在另一块三角板的边上，且，，，则 ______   度．


 

19.如图，四边形中，，对角线，相交于点，于点，于点，连接，，若，则下列结论：；；图中共有四对全等三角形；四边形是平行四边形；其中正确结论的是______．

20.如图，是▱的边的垂直平分线，垂足为点，与的延长线交于点连接，，，与交于点，则下列结论：
四边形是菱形；
；
：：；
：：．
其中正确的结论有______填写所有正确结论的序号

三、解答题（本大题共9小题，共72.0分）

21.如图，在的正方形网格中，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．
在图中，画一个直角三角形，使它的三边长都是有理数；
在图中，画一个直角三角形，使它的一边长是有理数，另外两边长是无理数；
在图中，画一个直角三角形，使它的三边长都是无理数．

22.如图，正方形，点，分别在，上，且，与相交于点．
求证：；
若，，求的长．

23.是等边三角形，点在的延长线上，以为中心，将线段逆时针旋转得线段，连接，．
如图，若，画出当时的图形，并写出此时的值；
为线段的中点，连接写出一个的值，使得对于延长线上任意一点，总有，并说明理由．

24.在中，为中点，、与射线分别相交于点、射线不经过点．
如图，当时，连接并延长交于点求证：四边形是平行四边形；
如图，当于点，于点时，分别取、的中点、，连接、、、求证：．

25.如图，折叠长方形纸片的一边，使点落在边的处，是折痕．已知，，求的长．

26.如图，在矩形中，对角线的中点为，点，在对角线上，，直线绕点逆时针旋转角，与边、分别相交于点、点不与点、重合．
求证：四边形是平行四边形；
若，，，求的长．

27.如图，在平行四边形中，以点为圆心，适当长的半径画弧，分别交、于点、，再分别以点、为圆心，大于长为半径画弧，两弧交于点，作射线交于点，交的延长线于点，分别过点、作、的平行线，并相交于点．
求证：四边形是菱形；
如图，若，，，求的长．

28.如图，，，点在上．

求证：平分；
求证：．

29.已知：在中，是边上的中线，点是的中点；过点作，交的延长线于，连接．
求证：四边形是平行四边形；
填空：
当时，四边形是______形；
当时，四边形是______形．