




还剩13页未读,
继续阅读
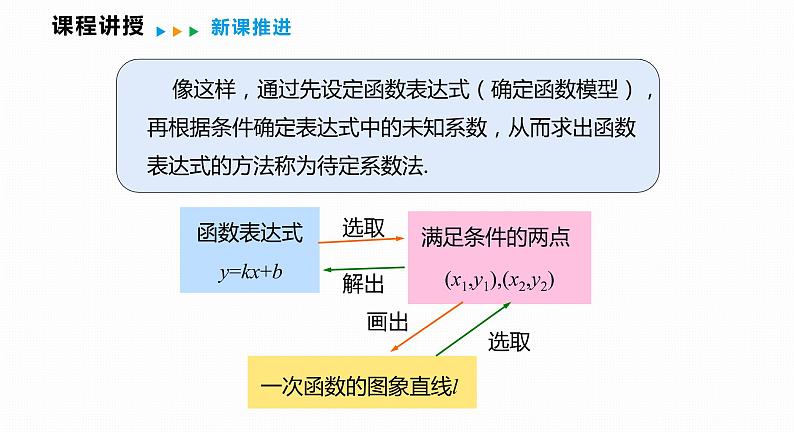
沪科版八年级上册12.2 一次函数备课ppt课件
展开
这是一份沪科版八年级上册12.2 一次函数备课ppt课件,共21页。PPT课件主要包含了学习目标及重难点,课程导入,课程讲授,新课推进,y-2x+1,随堂小练习,习题解析,习题1,习题2,习题3等内容,欢迎下载使用。
1. 会用待定系数法确定一次函数表达式;(重点)2. 经历待定系数法应用过程,体验数形结合.(难点)
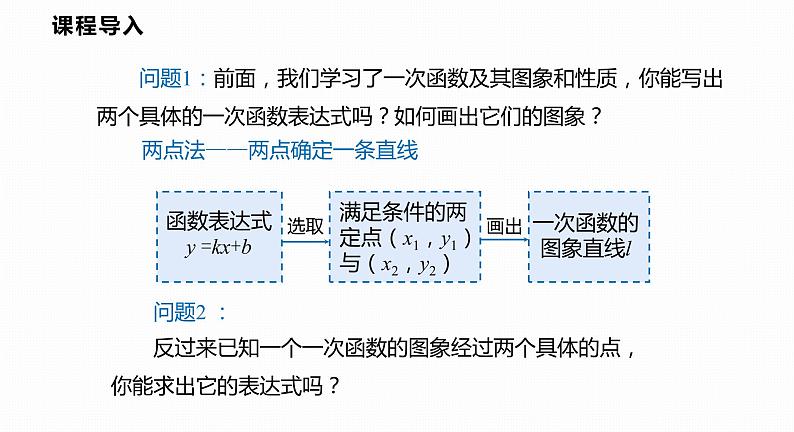
问题1:前面,我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数表达式吗?如何画出它们的图象?
问题2 : 反过来已知一个一次函数的图象经过两个具体的点,你能求出它的表达式吗?
两点法——两点确定一条直线
已知两个函数的图象如图所示,请根据图象写出每条直线的表达式.
由图象知,图1中直线的函数是正比例函数,其表达式为y=kx形式,关键是如何求出k的值;由图可知图象过点(1,2),所以该点坐标必适合表达式,将坐标代入y=kx得k=2.
反思:确定正比例函数和一次函数表达式各需几个条件?
确定正比例函数的表达式需要一个条件,确定一次函数的表达式需要两个条件.
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的表达式,关键是要确定k和b的值(即待定系数).
已知一次函数的图象过点(4,5)(5,2). 求这个一次函数的表达式.
因为图象过(4,5)与(5,2)点,所以这两点的坐标必适合表达式
1、已知 y是 x的一次函数,当 x=-1时 y=3,当 x =2 时 y=-3,求 y关于 x 的一次函数表达式.
2、若y与x-2成正比例关系,且x=4时y=5,求y关于x的函数关系.
3、已知直线 ,与直线 平行,且过点(4,6).求表达式.
利用二元一次方程组求一次函数表达式的一般步骤:1. 用含字母的系数设出一次函数的表达式 y=kx+b.2. 将已知条件代入上述表达式中得k,b的二元一次方程组.3. 解这个二元一次方程组得k,b.4. 进而求出一次函数的表达式.
问点A(-1,3),B(1,-1),C(3,-5)是否在同一条直线上.
解:设直线AB的表达式为y=kx+b.由题意得3=-k+b,-1=k+b,解得k=-2,b=1.∴直线AB:y=-2x+1.当x=3时,y=-2×3+1=-5,∴点C(3,-5)在直线AB上,因此,A、B、C三点共线.
一次函数y=kx+4的图象与y轴交于点B,与x轴交于点A,O为坐标原点,且△AOB的面积为4,求一次函数的表达式.
解:设直线l为y=kx+b, ∵l与直线y=-2x平行,∴k= -2. 又∵直线过点(0,2), ∴2=-2×0+b, ∴b=2, ∴直线l的表达式为y=-2x+2.
已知直线l与直线y=-2x平行,且与y轴交于点(0,2),求直线l的表达式.
已知一次函数的图象经过(0,5)、(2,-5)两点,求一次函数的表达式.
解:设一次函数的表达式为y=kx+b,根据题意得,∴-5=2k+b,5=b,解得b=5,k=-5.∴一次函数的表达式为y=-5x+5.
已知A是某正比例函数图象上一点,且点A在第二象限,作AP⊥x轴于P,AQ⊥y轴于Q,且AP=3,AQ=4,求正比例函数的表达式.
已知一次函数y=2x+m与x轴交于点A,与y轴交于点B,O是坐标原点,且S△AOB=4,求一次函数的表达式.
如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高h是指距d 的一次函数.下表是测得的指距与身高的一组数据:
(1)求出h与d之间的函数表达式.
(2)某人身高为196 cm,一般情况下他的指距应是多少?
正比例函数与一次函数的图象如图所示,它们的交点为A(4,3),B为一次函数的图象与y轴的交点,且OA=2OB.求正比例函数与一次函数的表达式.
1. 会用待定系数法确定一次函数表达式;(重点)2. 经历待定系数法应用过程,体验数形结合.(难点)
问题1:前面,我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数表达式吗?如何画出它们的图象?
问题2 : 反过来已知一个一次函数的图象经过两个具体的点,你能求出它的表达式吗?
两点法——两点确定一条直线
已知两个函数的图象如图所示,请根据图象写出每条直线的表达式.
由图象知,图1中直线的函数是正比例函数,其表达式为y=kx形式,关键是如何求出k的值;由图可知图象过点(1,2),所以该点坐标必适合表达式,将坐标代入y=kx得k=2.
反思:确定正比例函数和一次函数表达式各需几个条件?
确定正比例函数的表达式需要一个条件,确定一次函数的表达式需要两个条件.
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的表达式,关键是要确定k和b的值(即待定系数).
已知一次函数的图象过点(4,5)(5,2). 求这个一次函数的表达式.
因为图象过(4,5)与(5,2)点,所以这两点的坐标必适合表达式
1、已知 y是 x的一次函数,当 x=-1时 y=3,当 x =2 时 y=-3,求 y关于 x 的一次函数表达式.
2、若y与x-2成正比例关系,且x=4时y=5,求y关于x的函数关系.
3、已知直线 ,与直线 平行,且过点(4,6).求表达式.
利用二元一次方程组求一次函数表达式的一般步骤:1. 用含字母的系数设出一次函数的表达式 y=kx+b.2. 将已知条件代入上述表达式中得k,b的二元一次方程组.3. 解这个二元一次方程组得k,b.4. 进而求出一次函数的表达式.
问点A(-1,3),B(1,-1),C(3,-5)是否在同一条直线上.
解:设直线AB的表达式为y=kx+b.由题意得3=-k+b,-1=k+b,解得k=-2,b=1.∴直线AB:y=-2x+1.当x=3时,y=-2×3+1=-5,∴点C(3,-5)在直线AB上,因此,A、B、C三点共线.
一次函数y=kx+4的图象与y轴交于点B,与x轴交于点A,O为坐标原点,且△AOB的面积为4,求一次函数的表达式.
解:设直线l为y=kx+b, ∵l与直线y=-2x平行,∴k= -2. 又∵直线过点(0,2), ∴2=-2×0+b, ∴b=2, ∴直线l的表达式为y=-2x+2.
已知直线l与直线y=-2x平行,且与y轴交于点(0,2),求直线l的表达式.
已知一次函数的图象经过(0,5)、(2,-5)两点,求一次函数的表达式.
解:设一次函数的表达式为y=kx+b,根据题意得,∴-5=2k+b,5=b,解得b=5,k=-5.∴一次函数的表达式为y=-5x+5.
已知A是某正比例函数图象上一点,且点A在第二象限,作AP⊥x轴于P,AQ⊥y轴于Q,且AP=3,AQ=4,求正比例函数的表达式.
已知一次函数y=2x+m与x轴交于点A,与y轴交于点B,O是坐标原点,且S△AOB=4,求一次函数的表达式.
如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高h是指距d 的一次函数.下表是测得的指距与身高的一组数据:
(1)求出h与d之间的函数表达式.
(2)某人身高为196 cm,一般情况下他的指距应是多少?
正比例函数与一次函数的图象如图所示,它们的交点为A(4,3),B为一次函数的图象与y轴的交点,且OA=2OB.求正比例函数与一次函数的表达式.













