2022年浙江省温州市中考数学真题(word版含答案)

2022年温州中考数学试卷

数学

卷Ⅰ

一、选择题（本题有10小题，每小题4分，共40分．每小题只有一个选项是正确的，不选、多选、错选，均不给分）

1．计算的结果是（    ）

A．6     B．     C．3     D．

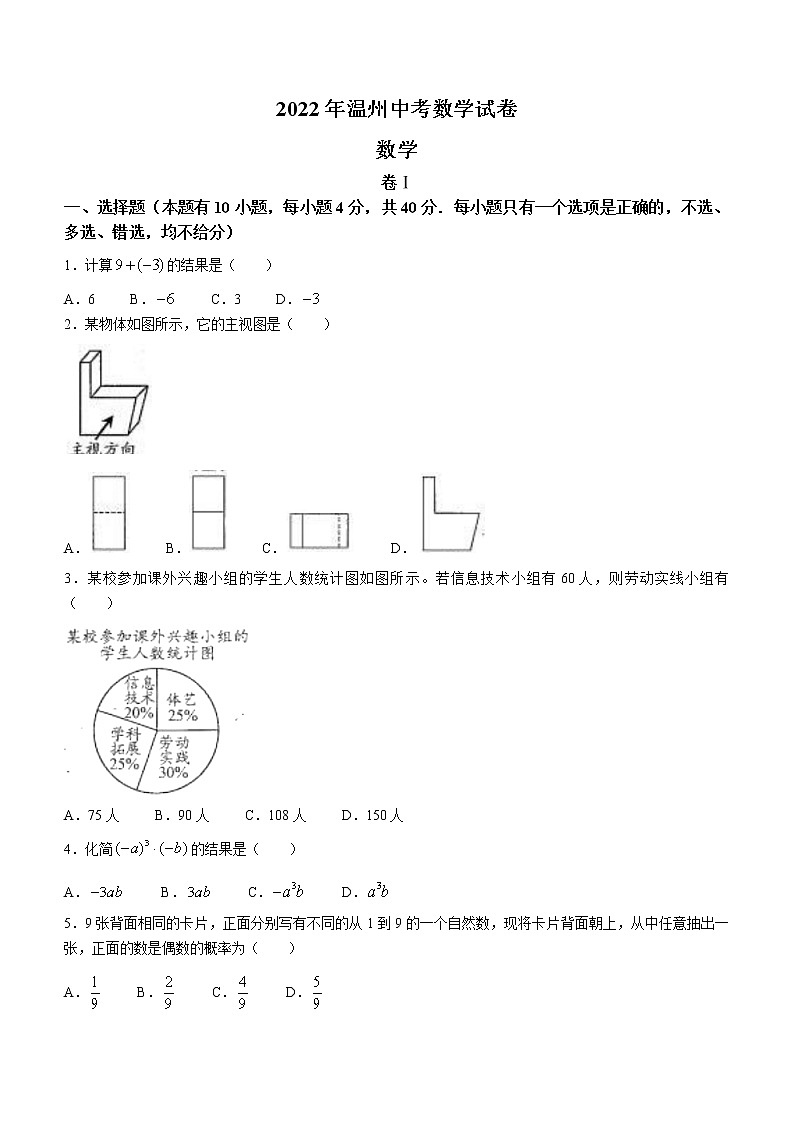
2．某物体如图所示，它的主视图是（    ）

A．     B．     C．     D．

3．某校参加课外兴趣小组的学生人数统计图如图所示。若信息技术小组有60人，则劳动实线小组有（    ）

A．75人     B．90人     C．108人     D．150人

4．化简的结果是（    ）

A．     B．     C．     D．

5．9张背面相同的卡片，正面分别写有不同的从1到9的一个自然数，现将卡片背面朝上，从中任意抽出一张，正面的数是偶数的概率为（    ）

A．     B．     C．     D．

6．若关于x的方程有两个相等的实数根，则c的值是（    ）

A．36     B．     C．9     D．

7．小聪某次从家出发去公园游玩的行程如图所示，他离家的路程为s米，所经过的时间为t分钟，下列选项中的图象，能近似刻画s与t之间关系的是（    ）

A．   B．   C．   D．

8．如图，是的两条弦，于点D，于点E，连结，．若，则的度数为（    ）

A．     B．     C．     D．

9．已知点都在抛物线上，点A在点B左侧，下列选项正确的是（    ）

A．若，则     B．若，则

C．若，则     D．若，则

10．如图，在中，，以其三边为边向外作正方形，连结，作于点M，于点J，于点K，交于点L．若正方形与正方形的面积之比为5，，则的长为（    ）

A．     B．     C．     D．

卷Ⅱ

二、填空题（本题有6小题，每小题5分，共30分）

11．分解因式：___________．

12．某校5个小组在一次拉树活动中植树株数的统计图如图所示，则平均每组植树___________株．

13．计算：___________．

14．若扇形的圆心角为，半径为，则它的弧长为___________．

15．如图，在菱形中，．在其内部作形状、大小都相同的菱形和菱形，使点E，F，G，H分别在边上，点M，N在对角线上．若，则的长为___________．

16．如图是某风车示意图，其相同的四个叶片均匀分布，水平地而上的点M在旋转中心O的正下方。某一时刻，太阳光线恰好垂直照射叶片，此时各叶片影子在点M右侧成线段，测得，垂直于地面的木棒与影子的比为2∶3，则点O，M之间的距离等于___________米．转动时，叶片外端离地面的最大高度等于___________米．

三、解答题（本题有8小题，共80分．解答需写出必要的文字说明、演算步骤或证明过程）

17．（本题10分）

（1）计算：．

（2）解不等式，并把解表示在数轴上．

18．（本题8分）如图，在的方格纸中，已知格点P，请按要求画格点图形（顶点均在格点上）．

（1）在图1中画一个锐角三角形，使P为其中一边的中点，再画出该三角形向右平移2个单位后的图形．

（2）在图2中画一个以P为一个顶点的钝角三角形，使三边长都不相等，再画出该三角形绕点P旋转后的图形．

注：图1，图2在答题纸上．

19．（本题8分）为了解某校400名学生在校午餐所需的时间，抽查了20名学生在校午餐所花的时间，由图示分组信息得：A，C，B，B，C，C，C，A，B，C，C，C，D，B，C，C，C，E，C，C．

某校被抽查的20名学生在校

午餐所花时问的频数表

（1）请填写频数表，并估计这400名学生午餐所花时间在C组的人数．

（2）在既考虑学生午餐用时需求，又考虑食堂运行效率的情况下，校方准备在15分钟，20分钟，25分钟，30分钟中选择一个作为午餐时间，你认为应选择几分钟为宜？说明现由．

20．（本题8分）如图，是的角平分线，，交于点E．

（1）求证：．

（2）当时，请判断与的大小关系，并说明理由．

21．（本题10分）已知反比例函数的图象的一支如图所示，它经过点．

（1）求这个反比例函数的表达式，并补画该函数图象的另一支．

（2）求当，且时自变量x的取值范围．

22．（本题10分）如图，在中，于点D，E，F分别是的中点，O是的中点，的延长级交线段于点G，连结．

（1）求证：四边形是平行四边形．

（2）当时，求的长．

23．（本题12分）根据以下素材，探索完成任务．

24．（本题14分）如图1，为半圆O的直径，C为延长线上一点，切半圆于点D，，交延长线于点E，交半圆于点F，已知．点P，Q分别在线段上（不与端点重合），且满足．设．

（1）求半圆O的半径．

（2）求y关于x的函数表达式．

（3）如图2，过点P作于点R，连结．

①当为直角三角形时，求x的值．

②作点F关于的对称点，当点落在上时，求的值．

数学参考答案

一、选择题（本题有10小题，每小题4分，共40分）

二、填空题（本题有6小题，每小题5分，共30分）

11．  12．5  13．2  14．  15．  16．10；

三、解答题（本题有8小题，共80分）

17．（本题10分）

解：（1）原式．

（2）移项，得．

合并同类项，得．

两边都除以2，得．

这个不等式的解表示在数轴上如图所示．

18．（本题8分）

解：（1）画法不唯一，如图1或图2等．

（2）画法不唯一，如图3或图4等．

19．（本题8分）

解：（1）频数表填写如表所示。

（名）．

答：这400名学生午餐所花时间在C组的有240名．

某校被袖查的20名学生在校午餐所花时间的频数表

（2）评分参考：

A等级：合理选择，完整说理．

①选择25分钟，有19人能按时完成用餐，占比95%，可以鼓励最后一位同学适当加快用餐速度，有利于食堂提高运行效率．

②选择20分钟，有18人能按时完成用餐，占比90%，可以鼓励最后两位同学适当加快用餐速度或采用合理照顾如优先用餐等方式，以满足学生午餐用时需求，又提高食堂的运行效率．

B等级：合理选择但理由不全面或选择不适当但有一定理由．

选择25分钟或选择20分钟，但理由不全面．

选择30分钟，能说明所有学生都能完成用餐，但未考虑食堂的运行效率．

C等级：只选择不说理或选择不适当，说理片面．

选择25分钟或选择20分钟或选择30分钟，未作说理或理由不合理；

选择15分钟，只考虑食堂的运行效率，未考虑全体学生午餐用时需求等因素．

D等级：选择15分钟而未作合理说理或未作答．

20．（本题8分）

证明：（1）∵是的角平分线，∴．

∵，∴，

∴．

（2）．理由如下：

∵，

∴．

∵，

∴，

∴，∴，

∴，即．

由（1）得，∴，

∴．

21．（本题10分）

解：（1）把点代入表达式，

得，∴，

∴反比例函数的表达式是．

反比例函数图象的另一支如图所示．

（2）当时，，解得．

由图象可知，当，且时，

自变量x的取值范围是或．

22．（本题10分）

解：（1）∵E，F分别是的中点，∴，

∴．

∵O是的中点，∴，

∴，∴，

∴四边形是平行四边形．

（2）∵，E是中点，

∴，∴，

∴，∴．

∵，∴．

∴．

由得．

23．（本题12分）

解：【任务1】

以拱顶为原点，建立如图1所示的直角坐标系，

则顶点为，且经过点．

设该抛物线函数表达式为，

则，∴，

∴该抛物线的函数表达式是．

【任务2】

∵水位再上涨达到最高，灯笼底部距离水面至少，灯笼长，

∴悬挂点的纵坐标，

∴悬挂点的纵坐标的最小值是．

当时，，解得或，

∴悬挂点的横坐标的取值范围是．

【任务3】有两种设计方案（解答时任给一种即可，该任务满分3分）．

方案一：如图2（坐标系的横轴，图3同），从顶点处开始悬挂灯笼．

∵，相邻两灯笼悬挂点的水平间距均为，

∴若顶点一侧挂4盏灯笼，则，

若顶点一侧挂3盏灯笼，则，

∴顶点一侧最多可挂3盏灯笼．

∵挂满灯笼后成轴对称分布，

∴共可挂7盏灯笼．

∴最左边一盏灯笼悬挂点的横坐标是．

方案二：如图3，从对称轴两侧开始悬挂灯笼，正中间两盏与对称轴的距离均为，

∵若顶点一侧挂5盏灯笼，则，

若顶点一侧挂4盏灯笼，则，

∴顶点一侧最多可挂4盏灯笼．

∵挂满灯笼后成轴对称分布，

∴共可挂8盏灯笼．

∴最左边一盏灯笼悬挂点的横坐标是．

注：以下为几种常见建系方法所得出的任务答案，其他方法酌情给分．

24．（本题14分）

解：（1）如图1，连结．设半圆O的半径为r．

∵切半圆O于点D，∴．

∵，∴，

∴，

∴，即，

∴，即半圆O的半径是．

（2）由（1）得：．

∵，∴．

∵，∴．

（3）①显然，所以分两种情况．

ⅰ）当时，如图2．

∵，∴．

∵，∴四边形为矩形，

∴．

∵，

∴，∴．

ⅱ）当时，过点P作于点H，如图3，

则四边形是矩形，∴．

∵，∴．

∵，

∴，

∴，

∴，∴，

由得：，∴．

综上所述，x的值是或．

②如图4，连结，由对称可知，

∴，

∴．

∵是半圆O的直径，∴，

∴，

∴，∴，

∴．

或利用得：．