还剩10页未读，继续阅读

下载需要10学贝 1学贝=0.1元

使用下载券免费下载

加入资料篮

立即下载

2021莆田高一下学期期末质量监测数学含答案

展开

这是一份2021莆田高一下学期期末质量监测数学含答案，共13页。

www.ks5u.com莆田市2020－2021学年下学期期末质量监测

高一数学试卷

本试卷共6页，22小题，满分150分。考试时间120分钟

注意事项：

1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1.若复数z＝1－2i5，则z的虚部是

A.－2 B.－2i C.2 D.2i

2.某射击运动员在同一条件下射击的成绩记录如表所示。

根据表中的数据，估计该射击运动员射击一次射中8环以上的概率为

A.0.78 B.0.79 C.0.80 D.0.82

3.若复数z满足i＝－3＋4i，则z＝

A.3－4i B.4－3i C.3＋4i D.4＋3i

4.已知向量a，b不共线，且向量a＋λb与(λ＋1)a＋2b共线，则实数λ的值为

A.－2或－1 B.－2或1 C.－1或2 D.1或2

5.一个不透明的袋子中装有8个红球，2个白球，除颜色外，球的大小、质地完全相同，采用不放回的方式从中摸出3个球。下列事件为不可能事件的是

A.3个都是白球 B.3个都是红球 C.至少1个红球 D.至多2个白球

6.设m，n是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是

A.若α//β，mα，nβ，则m//n B.若α∩β＝m，nβ，m⊥n，则n⊥α

C.若α⊥β，mα，nβ，则m⊥n D.若m⊥α，m//n，n//β，则α⊥β

7.△ABC的内角A，B，C的对边分别为a，b，c，若a＝3，c＝，C＝，则＝

A. B. C. D.3

8.古希腊数学家阿基米德一生最为满意的一个数学发现就是“圆柱容球”定理，即圆柱内切球的体积是圆柱体积的，且球的表面积也是圆柱表面积的。已知表面积为18π的圆柱的轴截面为正方形，则该圆柱内切球表面积与圆柱的体积之比为

A.2：3 B.2： C.：3 D.4：3

二、选择题：本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，部分选对的得2分，有选错的得0分。

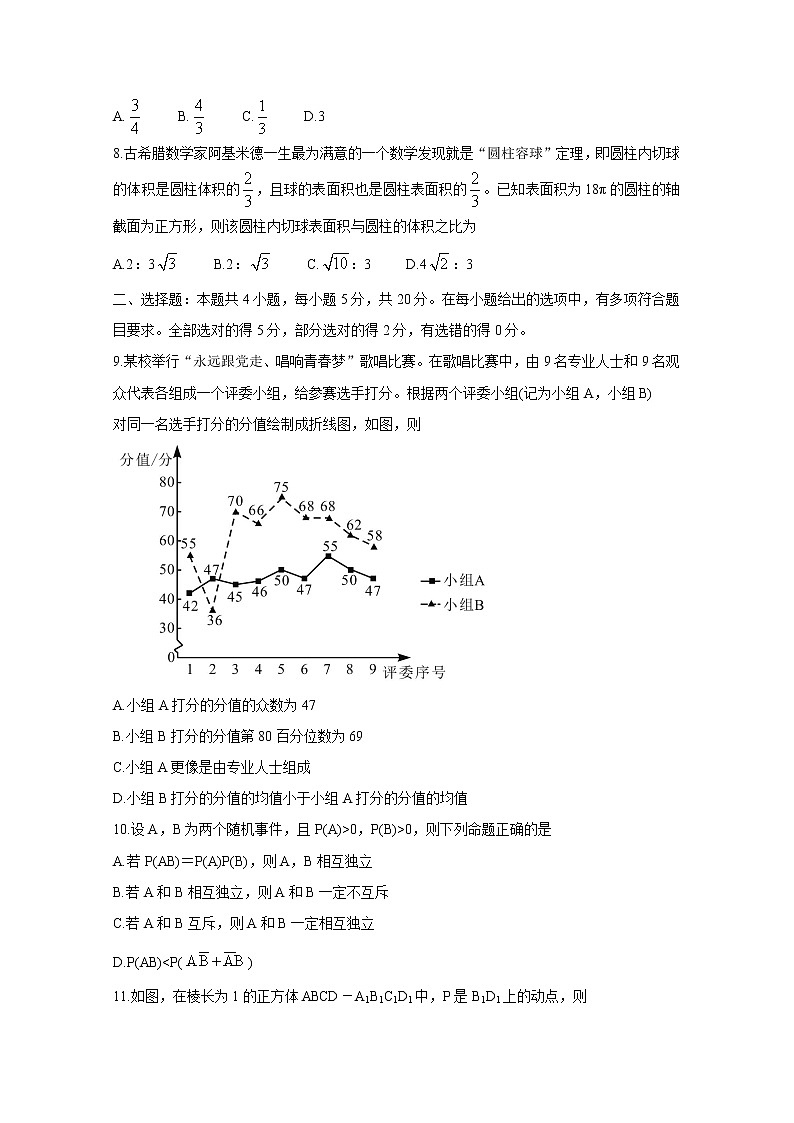
9.某校举行“永远跟党走、唱响青春梦”歌唱比赛。在歌唱比赛中，由9名专业人士和9名观众代表各组成一个评委小组，给参赛选手打分。根据两个评委小组(记为小组A，小组B)

对同一名选手打分的分值绘制成折线图，如图，则

A.小组A打分的分值的众数为47

B.小组B打分的分值第80百分位数为69

C.小组A更像是由专业人士组成

D.小组B打分的分值的均值小于小组A打分的分值的均值

10.设A，B为两个随机事件，且P(A)>0，P(B)>0，则下列命题正确的是

A.若P(AB)＝P(A)P(B)，则A，B相互独立

B.若A和B相互独立，则A和B一定不互斥

C.若A和B互斥，则A和B一定相互独立

D.P(AB)<P()

11.如图，在棱长为1的正方体ABCD－A1B1C1D1中，P是B1D1上的动点，则

A.直线DP与BC1是异面直线

B.CP//平面A1BD

C.A1P＋PB的最小值是2

D.当P与B1重合时，三棱锥P－A1BD的外接球半径为

12.点O，H分别为△ABC的外心，垂心，点D，M在平面ABC内，则下列命题正确的是

A.若，且，则向量在向量上的投影向量为

B.若，且，则

C.若＝0，则△ABC的面积与△AMB的面积之比为2：1

D.若＝0，则cos∠AHB＝－

三、填空题：本题共4小题，每小题5分，共20分。

13.某市有大型超市200家、中型超市400家、小型超市1400家。为了掌握各类超市的营业情况，现用比例分配的分层随机抽样方法抽取一个容量为100的样本，应抽取小型超市

家。

14.已知4件产品中恰有2件一等品，从中任取2件，恰有1件一等品的概率为。

15.△ABC中，AB＝1，AC＝2，∠BAC＝60°，点M，N分别在AC，BC上，且AM＝CM，BN＝2NC，AN，BM相交于点P，则cos∠MPN＝。

16.如图，一块斜边长为40cm的直角三角尺，其中一个内角为60°，把该角立在桌面上，使得斜边所在的直线与桌面所在的平面所成的角为45°，再绕其斜边旋转，则直角顶点到桌面距离的最大值为 cm。

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

17.(本小题满分10分)

已知向量a，b满足|a|＝1，|b|＝，(2a－b)·(a＋2b)＝1。

(1)求a与b的夹角θ；

(2)求|a－2b|的值。

18.(本小题满分12分)

如图，平面ACEF⊥平面ABC，AF⊥AC，AF//CE，AF＝CE，BD＝2BE。

(1)求证：DF//平面ABC；

(2)求证：DF⊥CE。

19.(本小题满分12分)

在①m＝(cosA，cosB)，n＝(b－2c，a)，且m⊥n，

②acosA＋acos(B－C)＝2bcosAsinC，

③(sinB－sinC)2＝sin2A－sinBsinC这三个条件中任选一个，补充在下面问题中，并解答。

问题：△ABC的内角A，B，C的对边分别为a，b，c，且。

(1)求A的值；

(2)若a＝2，求△ABC周长的最大值。

20.(本小题满分12分)

甲、乙两人进行乒乓球比赛，已知每局比赛甲获胜的概率为，乙获胜的概率为，且各局比赛的胜负互不影响。有两种比赛方案供选择，方案一：三局两胜制(先胜2局者获胜，比赛结束)；方案二：五局三胜制(先胜3局者获胜，比赛结束)。

(1)若选择方案一，求甲获胜的概率；

(2)用掷硬币的方式决定比赛方案，掷3枚硬币，若恰有2枚正面朝上，则选择方案一，否则选择方案二。判断哪种方案被选择的可能性更大，并说明理由。

21.(本小题满分12分)

如图1，Rt△ABC中，∠B＝90°，AB＝2，BC＝2，D，E分别是AB，AC的中点。把△ADE沿DE折至△PDE的位置，P平面BCED，连接PB，PC，F为线段PB的中点，如图2。

(1)求证：DF⊥平面PBC；

(2)当三棱锥P－BDE的体积为时，求直线BD与PC所成角的正切值。

22.(本小题满分12分)

为进一步推动防范电信网络诈骗工作，预防和减少电信网络诈骗案件的发生，某市开展防骗知识大宣传活动。该市年龄100岁及以下的居民人口约为300万人，从0岁到100岁的居民年龄频率分布直方图如图所示，其分组区间为：[0，20)，[20，40)，[40，60)，[60，80)，[80，100]。为了解防骗知识宣传的效果，随机调查了100名该市年龄100岁及以下居民对防骗知识的知晓情况，调查的知晓率(被调查的人群中，知晓的人数和总人数的比率)如表所示。