2022北京东城初三二模数学试卷（有答案）

这是一份2022北京东城初三二模数学试卷（有答案），共14页。试卷主要包含了选择题，填空题，解答题解答应写出文字说明等内容，欢迎下载使用。
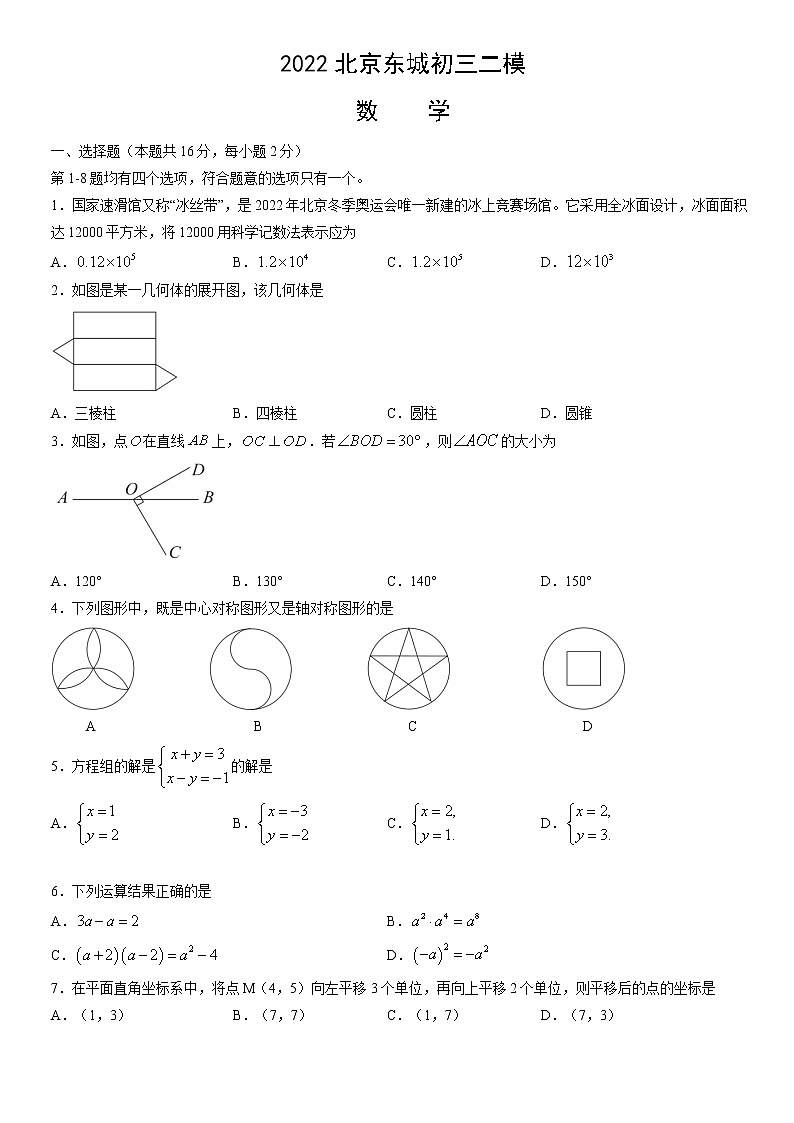
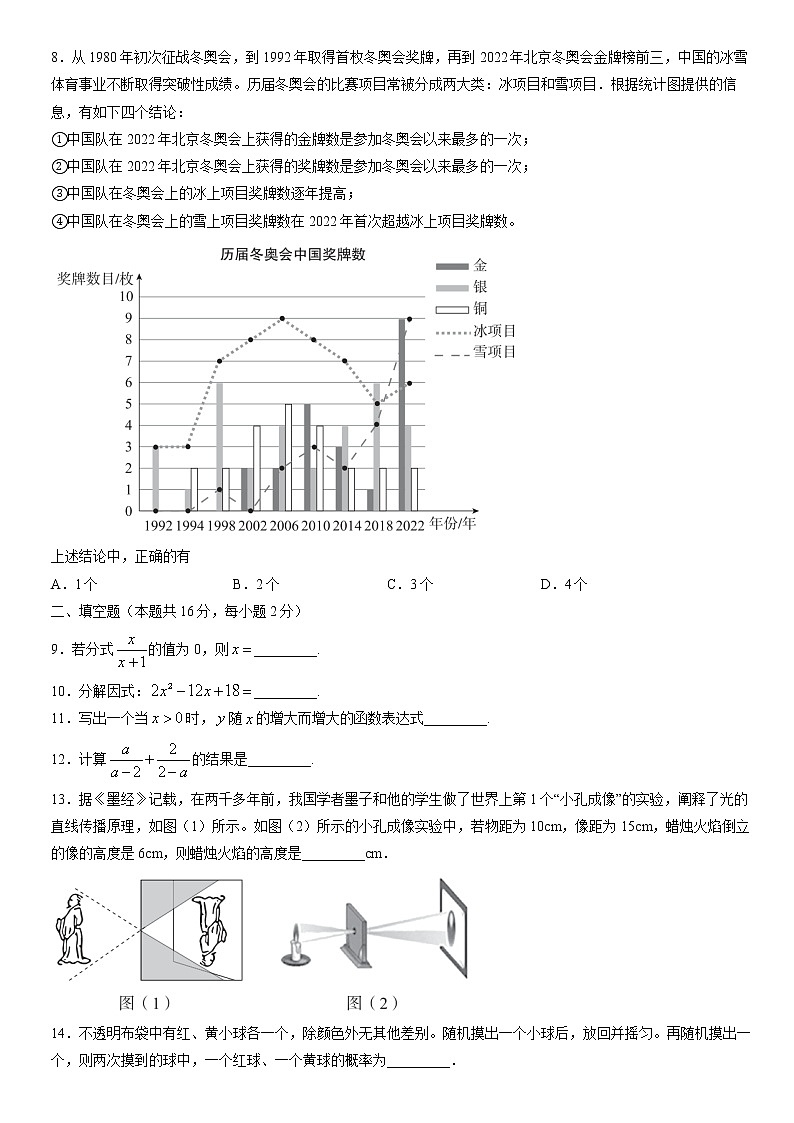
2022北京东城初三二模数    学一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个。1．国家速滑馆又称“冰丝带”，是2022年北京冬季奥运会唯一新建的冰上竞赛场馆。它采用全冰面设计，冰面面积达12000平方米，将12000用科学记数法表示应为A． B． C． D．2．如图是某一几何体的展开图，该几何体是A．三棱柱 B．四棱柱 C．圆柱 D．圆锥3．如图，点在直线上，．若，则的大小为A．120° B．130° C．140° D．150°4．下列图形中，既是中心对称图形又是轴对称图形的是A B C D5．方程组的解是的解是A． B． C． D． 6．下列运算结果正确的是A．  B．C．  D．7．在平面直角坐标系中，将点M（4，5）向左平移3个单位，再向上平移2个单位，则平移后的点的坐标是A．（1，3）              B．（7，7）              C．（1，7）              D．（7，3）8．从1980年初次征战冬奥会，到1992年取得首枚冬奥会奖牌，再到2022年北京冬奥会金牌榜前三，中国的冰雪体育事业不断取得突破性成绩。历届冬奥会的比赛项目常被分成两大类：冰项目和雪项目．根据统计图提供的信息，有如下四个结论：①中国队在2022年北京冬奥会上获得的金牌数是参加冬奥会以来最多的一次；②中国队在2022年北京冬奥会上获得的奖牌数是参加冬奥会以来最多的一次；③中国队在冬奥会上的冰上项目奖牌数逐年提高；④中国队在冬奥会上的雪上项目奖牌数在2022年首次超越冰上项目奖牌数。上述结论中，正确的有A．1个 B．2个 C．3个 D．4个二、填空题（本题共16分，每小题2分）9．若分式的值为0，则_________.10．分解因式：_________.11．写出一个当时，随的增大而增大的函数表达式_________.12．计算的结果是_________.13．据《墨经》记载，在两千多年前，我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验，阐释了光的直线传播原理，如图（1）所示。如图（2）所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是6cm，则蜡烛火焰的高度是_________cm．14．不透明布袋中有红、黄小球各一个，除颜色外无其他差别。随机摸出一个小球后，放回并摇匀。再随机摸出一个，则两次摸到的球中，一个红球、一个黄球的概率为_________．15．如图，在边长为1的正方形网格中，点在格点上，以为直径的圆过两点，则的值为_________．16．在一次数学活动课上，某数学老师将1～10共十个整数依次写在十张不透明的卡片上（每张卡片上只写一个数字，每一个数字只写在一张卡片上，而且把写有数字的那一面朝下）。他先像洗扑克牌一样打乱这些卡片的顺序，然后把甲、乙、丙、丁、戊五位同学叫到讲台上，随机地发给每位同学两张卡片，并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上，写出的结果依次是：甲：11；乙：4；丙：15；丁：8；戊：17，则丙同学手里拿的卡片的数字是_________．三、解答题（本题共68分，第17－21题，每小题5分，第22－23题，每小题6分，第24题5分，第25－26题，每小题6分，第27－28题，每小题7分）解答应写出文字说明、演算步骤或证明过程17．计算：．18．解不等式，并写出其正整数解。19．如图，在中，．求作：直线，使得．小明的作法如下：①以点为圆心、适当长为半径画弧，交的延长线于点，交线段于点；②分别以点为圆心、大于的长为半径画弧，两弧在的内部相交于点；③画直线．直线即为所求，（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；（2）完成下面的证明。证明：由作法可知：平分．∴（______________）．（填推理的依据）∵，∴∵，∴．∵，∴__________．∴ （________________________________________）．（填推理的依据）20．已知关于的一元二次方程．（1）不解方程，判断此方程根的情况；（2）若是该方程的一个根，求代数式的值．21．如图，在平行四边形中，，点是的中点，连接并延长，交的延长线于点，连接．（1）求证：四边形是菱形；（2）若，，求菱形的边长。22．如图，在平面直角坐标系中，双曲线经过点，直线：经过点．（1）求的值；（2）过点作垂直于轴的直线，与双曲线交于点，与直线交于点．①当时，判断与的数量关系；②当时，结合图象，直接写出的取值范围．23．如图，在中，，，在上截取，过点作于点，连接AD，以点为圆心、的长为半径作．（1）求证：是⊙A的切线；（2）若，，求的长．24．某研究中心建立了自己的科技创新评估体系，并对2021年中国城市的科技创新水平进行了评估。科技创新综合指数由科技创新总量指数和科技创新效率指数组成（以下简称：综合指数、总量指数和效率指数）。该研究中心对2021年中国城市综合指数得分排名前40的城市的有关数据进行收集、整理、描述和分析。下面给出了部分信息：a．综合指数得分的频数分布表（数据分成6组：，，，，）：综合指数得分频数816821合计40b．综合指数得分在这一组的是：70.0  70.4  70.6  70.7  71.0  71.0  71.1  71.2  71.8  71.9  72.5  73.8  74.0  74.4  74.5  74.6c．40个城市的总量指数与效率指数得分情况统计图：（数据来源于网络《2021年中国城市科技创新指数报告》）根据以上信息，回答下列问题：（1）综合指数得分的频数分布表中，______________；（2）40个城市综合指数得分的中位数为____________；（3）以下说法正确的是____________．①某城市创新效率指数得分排名第1，该城市的总量指数得分大约是86.2分；②大多数城市效率指数高于总量指数，可以通过提升这些城市的总量指数来提升城市的综合指数．25．小强用竹篱笆围一个面积为平方米的矩形小花园，他考虑至少需要几米长的竹篱笆（不考虑接缝），根据学习函数的经验，他做了如下的探究，请你完善他的思考过程．（1）建立函数模型：设矩形小花园的一边长为米，则矩形小花园的另一边长为__________米（用含的代数式表示）；若总篱笆长为米，请写出总篱笆长（米）关于边长（米）的函数关系式__________；（2）列表：根据函数的表达式，得到了与的几组对应值，如下表：12345106表中__________， __________；（3）描点、画出函数图象：如图，在平面直角坐标系中，将表中未描出的点，补充完整，并根据描出的点画出该函数的图象；（4）解决问题：根据以上信息可得，当_____________时，有最小值。由此，小强确定篱笆长至少为_________米。26．在平面直角坐标系中，抛物线的对称轴是直线．（1）直接写出抛物线与轴的交点坐标；（2）求抛物线的顶点坐标（用含的式子表示）；（3）若抛物线与轴相交于两点，且，求的取值范围。27．如图，在中，，，在△ABC的外侧作直线，作点关于直线的对称点，连接交直线于点．（1）依题意补全图形；（2）连接，求证：；（3）过点作于点，用等式表示线段之间的数量关系，并证明。28．在平面直角坐标系中，对于图形及过定点的直线，有如下定义：过图形上任意一点作于点，若有最大值，那么称这个最大值为图形关于直线的最佳射影距离，记作，此时点称为图形关于直线的最佳射影点。（1）如图1，已知，，写出线段关于轴的最佳射影距离____________；（2）已知点，的半径为，求关于轴的最佳射影距离，并写出此时关于轴的最佳射影点的坐标；（3）直接写出点关于直线的最佳射影距离的最大值．
参考答案一、选择题（本题共16分，每小题2分）题号12345678答案BAADACCC二、填空题（本题共16分，每小题2分）9． 10． 11. y=2x(答案不唯一)                                    12．1  13．4  14．  15．  16．10和5三、解答题（本题共68分，第17-21题，每小题5分，第22-23题，每小题6分，第24题5分，第25-26题，每小题6分，第27-28题，每小题7分）解答应写出文字说明、演算步骤或证明过程。17．解：   4分=1．  5分18．解：，，2分． 3分∵是正整数，∴．5分19．解：图略；角平分线的定义；；同位角相等，两直线平行． 5分20．解：（1）∵，∴方程有两个不相等的实数根．  2分（2）将代入方程，得．即．  4分则．  5分5分21．（1）证明：∵四边形是平行四边形，∴．∴．∵点是的中点，∴．在和中，，∴．∴．∵，∴四边形是平行四边形。∵，∴四边形是菱形．  2分（2）解：∵四边形是平行四边形，∴，．∴．．∴．∵四边形是菱形，∴, ,．∴∴．∵，∴，．由勾股定理，得．∴菱形的边长为5．  5分22．解：（1）∵双曲线经过点，∴．直线经过点，∴．   2分（2）①当时，，，∴．②．  6分23．（1）证明：如图，过点作于．∵，∴．∵，∴．∴．∴．∵，∴．∴．∵,，∴．∴AF=AE．∵,为半径，∴是的切线．  3分（2）解：∵，，∴．∵，∴．∵，∴．∴．∴．∴．  6分24．解：（1）5．  1分（2）73．9．   3分（3）②  5分25．解：（1）；．  2分（2）；10．  4分（3）图略．  5分（4）；6  6分26．解：（1）（0,1）．  1分（2）∵抛物线的对称轴是直线， ∴．∴．∴抛物线的解析式为．当时，．∴顶点坐标为．  3分（3）①当时，抛物线开口向下。不妨设点在点左侧。∵抛物线与轴交于点，且两点关于抛物线的对称轴（直线）对称，∴，．∴，不符合题意。②当时，抛物线开口向上。在轴上关于直线对称且距离为4的两点的坐标为（1,0），（5,0）．∵，∴当时．即．又∵抛物线与轴相交于两点，∴y顶点．∴综上所述，的取值范围．  6分27．（1）解：补全图形如下：  1分（2）证明：∵点与点关于直线对称，∴,．在和中，，∴． ∴．∵，∴．∴．∴．  3分（3）解：结论：．证明：如图，在上取一点，使．在和中， ∴．∴．∵，∴．∴．∴．  7分28．解：（1）3．  2分（2），或．  5分（3）．  7分