山东省菏泽市2022届高三下学期5月二模考试数学试题（Word版含答案）

2022年菏泽市高三二模考试

数学试题

一、选择题：本题共8小题，每小题5分，共40分在每小题给出的四个选项中，只有一项是符合题目要求的．

1．设集合，，则（    ）

A．   B．   C．  D．

2．已知复数z满足，则z为实数的一个充分条件是（    ）

A．   B．   C．   D．

3．已知双曲线的一条渐近线方程为，则下列说法正确的是（    ）

A．E的焦点到渐近线的距离为2    B．

C．E的实轴长为6       D．E的离心率为

4．民间娱乐健身工具陀螺起源于我国，最早出土的石制陀螺是在山西夏县新时期时代遗址发现的．如图所示的是一个陀螺的立体结构图，已知底面圆的直径cm，圆柱体部分的高cm，圆锥体部分的高cm，则这个陀螺的表面积是（    ）

A．   B．   C．   D．

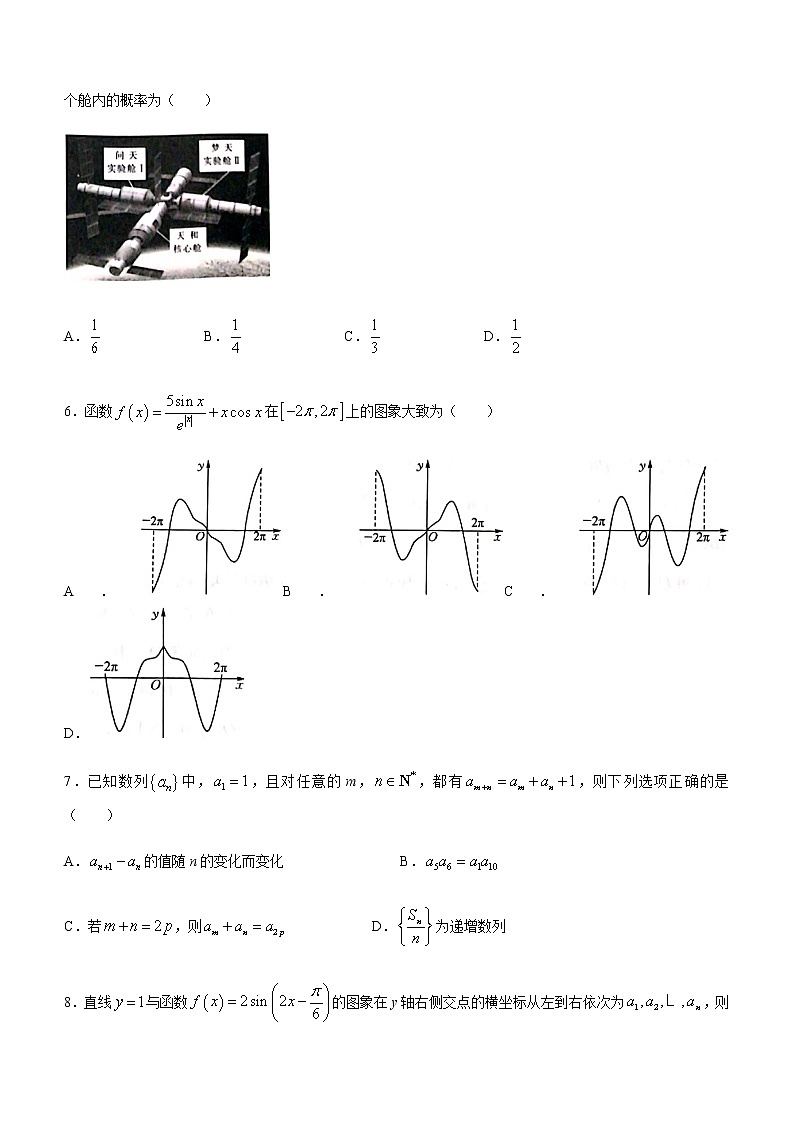
5．中国空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱，假设空间站要安排甲、乙、丙、丁4名航天员开展实验，其中天和核心舱安排2人，问天实验舱与梦天实验舱各安排1人，则甲乙两人安排在同一个舱内的概率为（    ）

A．    B．    C．    D．

6．函数在上的图象大致为（    ）

A．B．C．D．

7．已知数列中，，且对任意的m，，都有，则下列选项正确的是（    ）

A．的值随n的变化而变化     B．

C．若，则    D．为递增数列

8．直线与函数的图象在y轴右侧交点的横坐标从左到右依次为，则下列结论正确的是（    ）

A．    B．在上是减函数

C．为等差数列    D．

二、选择题：共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求全部选对的得5分，有选错的得0分，部分选对的得2分．

9．设离散型随机变量X的分布列为

若离散型随机变量Y满足：，则下列结果正确的有（    ）

A．   B．   C．   D．

10．设a，b为两个正数，定义a，b的算术平均数为，几何平均数为．上个世纪五十年代，美国数学家D.H. Lehmer提出了“Lehmer均值”，即，其中p为有理数．下列结论正确的是（    ）

A．    B．

C．    D．

11．已知椭圆的左右焦点分别为，，直线与椭圆E交于A，B两点，C，D分别为椭圆的左右顶点，则下列命题正确的有（    ）

A．若直线CA的斜率为，BD的斜率，则

B．存在唯一的实数m使得为等腰直角三角形

C．取值范围为

D．周长的最大值为

12．将边长为2的正方形ABCD沿对角线AC折起，使点D不在平面ABC内，则在翻折过程中，下列结论正确的有（    ）

A．存在某个位置，使直线BD与平面ABC所成的角为45°

B．当二面角为时，三棱锥的体积为

C．当平面ACD⊥平面ABC时，异面直线AB与CD的夹角为60°

D．O为AC的中点，当二面角为时，三棱锥外接球的表面积为

三、填空题：本题共4小题，每小题5分，共20分．

13．已知圆内有一点，AB为过点P且倾斜角为135°的弦，则______．

14．写出一个同时具有下列性质①②③的函数的解析式______．

①；②是偶函数；③在上单调递增．

15．已知半径为1的圆O上有三个动点A，B，C，且，则的值为______．

16．定义为与x距离最近的整数，令函数，如：，．则

______；______．

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程和演算步骤．

17．（10分）在中，角A，B，C的对边分别为a，b，c，且，．

（1）若，求A；

（2）若的面积，求c．

18．（12分）为了培养孩子的终身锻炼习惯，小明与小红的父亲与他们约定周一到周日每天的锻炼时间不能比前一天少．为了监督两人锻炼的情况，父亲记录了他们某周内每天的锻炼时间（单位：min），如下表所示，其中小明周日的锻炼时间a忘了记录，但知道，．

（1）求这一周内小明锻炼的总时间不少于小红锻炼的总时间的概率；

（2）根据小明这一周前6天的锻炼时间，求其锻炼时间y关于序号x的线性回归方程，并估计小明周日锻炼时间a的值．

参考公式：回归方程中斜率与截距的最小二乘估计公式分别为

，

参考数据：；

．

19．（12分）已知数列中，它的前n项和满足．

（1）证明：数列为等比数列；

（2）求．

20．（12分）如图，在四棱锥中，底面ABCD是边长为2的正方形，，，，的面积是的面积的倍．

（1）证明：平面PAD⊥平面ABCD；

（2）若E为BC的中点，F为线段PE上的任意一点，当DF与平面PBC所成角的正弦值最大时，求平面FAD与平面ABCD所成角的正切值．

21．（12分）已知抛物线的焦点为F，O为坐标原点，抛物线E上不同的两点M，N只能同时满足下列三个条件中的两个：

①；②；③直线MN的方程为．

（1）问M，N两点只能满足哪两个条件（只写出序号，无需说明理由）？并求出抛物线E的标准方程；

（2）如图，过F的直线与抛物线E交于A，B两点，过A点的直线l与抛物线E的另一交点为C，与x轴的交点为D，且，求三角形ABC面积的最小值．

22．（12分）设函数．

（1）当时，恒成立，求k的最大值；

（2）设数列的通项，证明：．

高三二模数学参考答案

一、二选择题

三、填空题

13．  14．或（满足条件即可） 15．  16．3；

四、解答

17．解：（1）因为，则，

由正弦定理，得，即，即，

因为，所以，因此；

（2）由，得，

．

当时，由余弦定理，得；

当时，由余弦定理，得．

所以，或．

18．解：（1）因为且，所以a的取值共有25种情况，

又当小明锻炼的总时间不少于小红时，有，即，

所以小明锻炼的总时间不少于小红时，a的取值共有17情况，

所以这一周内小明锻炼的总时间不少于小红的概率为．

（2）由题设可知，

，，

所以，，

所以y关于序号x的线性回归方程为．

当时，，

估计小明周日锻炼时间a的值为38．

19．解：（1）由①，得②，

由①－②，得，

得，

又当时，由①得，

所以对任意的，都有，

故是以为首项，为公比的等比数列．

（2）由（1）知

所以，代入①，得，

所以

．

20．（1）证明：由，，

，得，所以

取AD中点为O，E为BC中点，连接PO，OE，

则，，即为二面角的平面角，

由，，，所以，

因此，平面PAD⊥平面ABCD．

（2）以O为坐标原点，OA，OE，OP所在直线分别为x轴，y轴，

Z轴，建立如图的空间直角坐标系．则，，，，

设，则，，，，

设平面PBC的法向量为，则，取，

设DF与平面PBC所成角为，则，，

，当时，

取得最大值．此时，

由AD⊥平面POE，所以为平面PAD与

平面ABCD所成的二面角的平面角，．

21．解：（1）同时满足的条件为②③；

由知三角形OMN为等边三角形，且；

由，得，得，

得，，所以；

（2）设，联立消x，得，

设，，不妨设A点在轴上方，

则，，，，，

，

由，所以，则，联立，

得，．

C到AB距离

．

当且仅当时，面积取到最小值16．

22．解：（1），

①当时，由，得，

所以单调递增，又，因此恒成立；

②当时，令，则

，当，得，

所以在上，，单调递减，又，所以，

即，所以单调递减，又，所以，不满足要求．

综上，．

（2）由

，

要证，即证，

即证明：．

由（1），即，

取（），得，所以

累加得：，所以．