2021-2022学年重庆市北碚区西南大学附中九年级（下）期中数学试卷（无答案）

2021-2022学年重庆市北碚区西南大学附中九年级（下）期中数学试卷

一、选择题：本大题12个小题，每小题4分，共48分.在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑。

1．2的绝对值是（　　）

A．-2 B．2 C．- D．

2．2022年北京冬奥会完美落幕，吉祥物冰墩墩受到了人们的喜爱．其中一款摇摆手摆件，在奥林匹克官方旗舰店的月销量约90万个．将数据90万用科学记数法表示为（　　）

A．9×104 B．9×105 C．9×106 D．9×107

3．中国的华容道，法国的独立钻石棋，匈牙利的魔方，并称为智力游戏界的三大不可思议．下列魔方中，主视图形如三角形的是（　　）

4．如图，在平面直角坐标系中，将△OAB以原点为位似中心放大后得到△OCD，若A（1，0），C（3，0），则△OAB与△OCD的面积比为（　　）

A．1：2 B．1：3 C．1：4 D．1：9

5．关于抛物线y=-3（x+1）2+1的图象，下列说法错误的是（　　）

A．开口向下   B．对称轴是直线x=-1  C．顶点坐标为（1，1） D．与x轴有两个交点

6．下列计算中，正确的是（　　）

A．3+  B.  C.  D.

7．如图，AC是⊙O的直径，AB，BC是⊙O的弦，CD是⊙O的切线，C为切点，OD与⊙O交于点E．若点C为BE的中点，∠D=32°，则∠ACB的度数为（　　）

A．56° B．58° C．61° D．68°

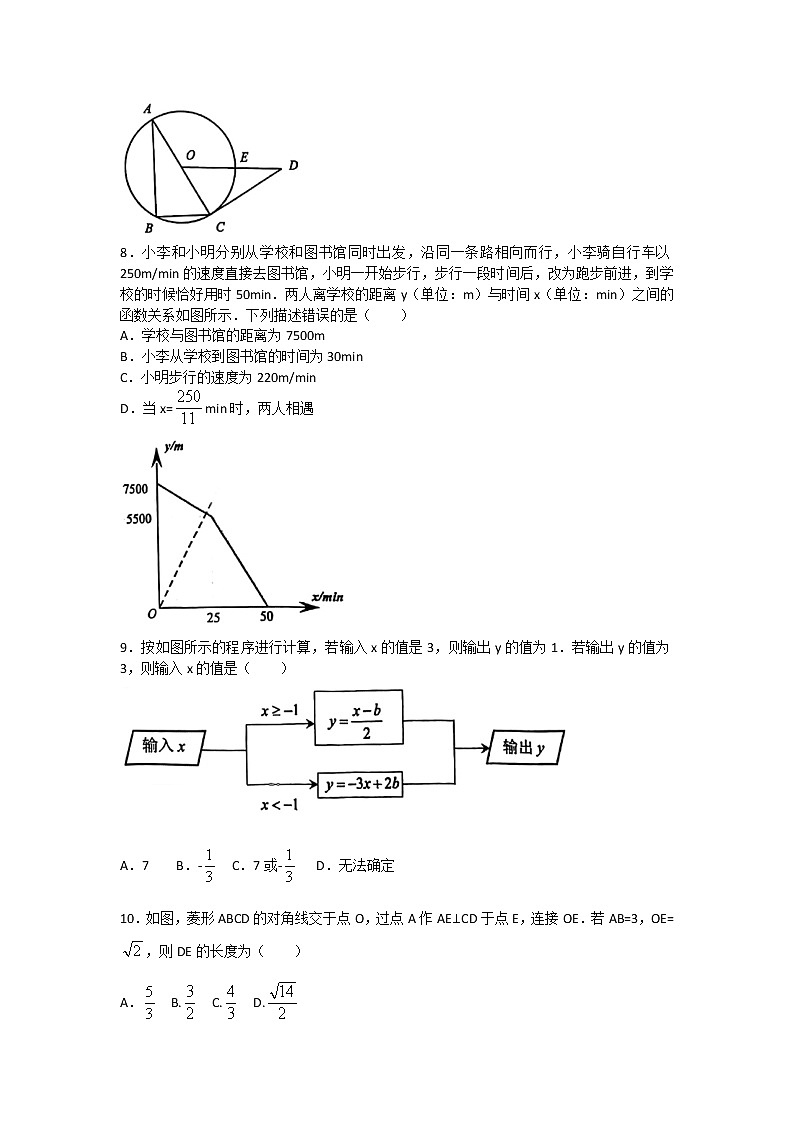
8．小李和小明分别从学校和图书馆同时出发，沿同一条路相向而行，小李骑自行车以250m/min的速度直接去图书馆，小明一开始步行，步行一段时间后，改为跑步前进，到学校的时候恰好用时50min．两人离学校的距离y（单位：m）与时间x（单位：min）之间的函数关系如图所示．下列描述错误的是（　　）

A．学校与图书馆的距离为7500m

B．小李从学校到图书馆的时间为30min

C．小明步行的速度为220m/min

D．当x=min时，两人相遇

9．按如图所示的程序进行计算，若输入x的值是3，则输出y的值为1．若输出y的值为3，则输入x的值是（　　）
 

A．7 B．- C．7或-  D．无法确定

10．如图，菱形ABCD的对角线交于点O，过点A作AE⊥CD于点E，连接OE．若AB=3，OE=，则DE的长度为（　　）

A．  B.  C.  D.

11．若关于x的一元一次不等式组的解集是x＞4，且关于y的分式方程=3有整数解，则符合条件的所有整数a的和为（　　）

A．-4 B．-3 C．-1 D．0

12．已知正整数a，b，c，d满足a＜b＜c＜d，且a+b+c+d=d2-c2+b2-a2，关于这个四元方程下列说法正确的个数是（　　）
①a=1，b=2，c=3，d=4是该四元方程的一组解；
②连续的四个正整数一定是该四元方程的解；
③若a＜b＜c＜d＜10，则该四元方程有21组解；
④若a+b+c+d=2022，则该四元方程有504组解．

A．1 B．2 C．3 D．4

二、填空题：本大题共4个小题，每小题4分，共16分。请将每小题的答案直接填在答题卡对应的横线上

13．计算sin30°++2-1=_________.

14．现有四张正面分别标有数字-2，-1，0，1的不透明卡片，它们除数字外其余完全相同，将它们的背面朝上洗均匀，随机抽取一张，记下数字放回，背面朝上洗均匀，再随机抽取一张记下数字．前后两次抽取的数字分别记为m，n．则点P（m，n）出现在第二象限的概率为 ________.

15．如图，在矩形ABCD中，BC=1，AB=2．以点A为圆心，AB的长为半径画弧交DC于点F．以点D为圆心，DA的长为半径画弧交DC于点E．则图中阴影部分的面积为 _________．（结果保留π）

16．小李和小张一起承包36亩的土地作为果园基地．他们将36亩土地分成一号、二号、三号区域，三个区域的土地面积均为整数亩，分别用于种植苹果树、桃树、梨树其中的一种（每块区域可任意选择三种果树的一种，同一块区域只能种同一种果树）．小李和小张提出两种种植方案，小李的方案为：在一号区域种苹果、二号区域种桃树、三号区域种梨树；小张的方案为：在一号区域种苹果、在二号区域种梨树、在三号区域种桃树，每种树苗按亩计价，且单价为整数，苹果树苗每亩100元，桃树苗比梨树苗贵，且每亩差价不大于14元，不小于8元，苹果树苗占整个种植树苗的十二分之五，小李方案中，桃树和梨树共花费1590元，小张的方案比小李的方案少花30元．应如何安排三个区域种植树苗的类型，可以使花费最少，最少花费为 ________元．

三、解答题：本大题2小题，每小题8分，共16分。解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上。

17．计算：
（1）（x+y）2-y（x+y）；
（2）．

18．在▱ABCD中，BE⊥CD于点E．
（1）尺规作图：在AB上取一点F，使DA=DF，连接DF，过点D作AB的垂线，垂足为G．（不写作法，不下结论，保留作图痕迹）；
（2）在（1）所作的图形中，证明CE=AF．请完成下列证明过程：
证明：∵DA=DF且DG⊥AB
∴∠AGD=90°，
AG=AF（ _________________）（填写推理依据）
∵四边形ABCD是平行四边形
∴∠A=_______，
AD=BC
∵BE⊥CD
∴∠CEB=90°
在△ADG和△CBE中
∠AGD=∠CEB
∠A=∠C
AD=BC
∴△ADG≌△CBE（ _________）
∴CE=_________
∴CE=AF．

四、解答题：本大题7小题，每小题10分，共70分。解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上。

19．2022年3月11日晚，重庆新增3例本土新冠肺炎确诊病例，疫情发生后，重庆某中学高度重视，积极配合市政府的防疫工作，当晚立即在微信上的家长群发布疫情情况统计表，对学生及家长进行摸排．3月12日上午8点，学校防疫小组从该学校的八年级和九年级中各随机抽取了15个班级，对班级填报人数情况进行收集、整理、分析后得到如下信息．
八年级15个班级填报人数分别为：
45，42，41，52，50，53，55，52，52，50，52，43，49，51，48．
九年级15个班级填报人数条形统计图如图：
抽取的八、九年级的班级填报人数的平均数、众数、中位数及极差如下表所示：

根据以上信息，解答以下问题：
（1）直接写出上表中a，b，c的值：a=_____；b=_____；c=______；
（2）你认为该校八年级和九年级中哪个年级的填报情况更好？请说出你的理由；
（3）填报人数达到或超过50人的班级，视为“防疫积极班级”，若该校有90个班级，试估算该校“防疫积极班级”有多少个？

20．如图是某人行天桥的示意图，坡面AB的长度为10米，坡度为1：．为了方便行人推车过天桥，有关部门决定降低坡度，使新坡而AC的坡度为1：．
（1）求新坡面AC的长度；
（2）若需在C点的左侧留出3米的通道，判断距离B点5米的文化墙PM是否需要拆除？请说明理由．（参考数据：≈1.7）
 

21．如图，在平面直角坐标系中，一次函数y=mx+n（m≠0）与反比例函数y=（k≠0）交于A，B（-3，-2）两点，其中点A的横坐标为1．
（1）求一次函数和反比例函数的解析式；
（2）将一次函数向下平移8个单位长度后，与x轴交于点C，连接CA，CB，求△ABC的面积；
（3）请结合图象，直接写出不等式mx+n≥的解集．

22．某玩具店两周前以40元一个的价格购进一批玩偶，原定以50%的利润率定价，但由于销路不好导致商品积压，于是在周末调价时打折促销，通过两次打折调价，每次打折力度相同，现在的售价为每个48.6元，
（1）请问该批玩偶每次打几折？
（2）若玩偶库存共20个，计划通过两次相同力度打折调价，清空所有库存，并保证两次降价后销售的总利润不少于200元，则第一次降价至少售出多少件玩偶，才可以进行第二次降价？

23．对于一个各个数位不为0的三位数，从它的百位、十位、个位上任取两个数字可生成一个两位数，那么这个三位数可以生成6个两位数，称这6个两位数为原来三位数的“次生数”．例如：三位数123的6个“次生数”为12，13，21，23，31，32．将一个两位数m的十位数字乘以8，再加上m的个位数字，得到的结果称为m的“八一数”，记作F（m）．例如：m=23，因为2×8+3=19，所以23的“八一数”是19，记作F（23）=19，将一个三位数n的所有“次生数”的“八一数”的和记为H（n），例如：H（123）=F（12）+F（13）+F（21）+F（23）+F（31）+F（32）=10+11+17+19+25+26=108．
（1）计算H（857）；
（2）证明：任意一个三位数的所有“次生数”的“八一数”的和能被18整除；
（3）已知一个三位数n=100a+20+3c，其中1≤a≤5，1≤c≤5且a，c是整数，H（n）是完全平方数，求出所有满足条件的三位数n．

24．如图1，抛物线y=ax2+bx+c（a≠0）与直线y=-x+4的交点分别位于x轴、y轴上的A、B两点，与x轴的另一交点为C（-2，0）．
（1）求抛物线的解析式；
（2）如图2，连接BC，点P为AB上方抛物线上一动点，过点P作PQ∥BC交AB于点Q，过点P作PR⊥x轴交AB于点R．求△PQR周长最大值及此时点P的坐标；
（3）在（2）问条件下，当△PQR面积最大时，将△PQR绕点R顺时针旋转n°（0＜n＜90），当旋转过程中，PR⊥AB时，记此时三角形为△P1Q1R1，再将△P1Q1R1沿直线AB进行翻折得到△P2Q2R2，将△P2Q2R2沿直线AB进行平移，在平移过程中，若点P2恰好在抛物线上，记此时的三角形为△P3Q3R3，请直接写出此时P3的坐标．
 

25．如图1，△ABC中，AB=BC，AB⊥BC，△DEB中，BD⊥BE，点C是△DEB中DE边上一点，点F是DE下方一点，连接DF、EF、BF，BF交AC于点G，∠AEC=∠DFE=90°．
（1）若∠AGB=60°，AB=2，求CG长度．
（2）若DF=3DC，证明：3AE+EF=BF．
（3）如图2，将△EDF沿EF翻折得到△ED'F，过点D作DM⊥D'E，在线段ED'上截取EN=DM，连接FN，若EF=2，求FN的最小值．