2022届广东省广州市玉岩中学中考猜题数学试卷含解析

这是一份2022届广东省广州市玉岩中学中考猜题数学试卷含解析，共21页。

2021-2022中考数学模拟试卷
注意事项
1．考试结束后，请将本试卷和答题卡一并交回．
2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．
3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．
4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．
5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
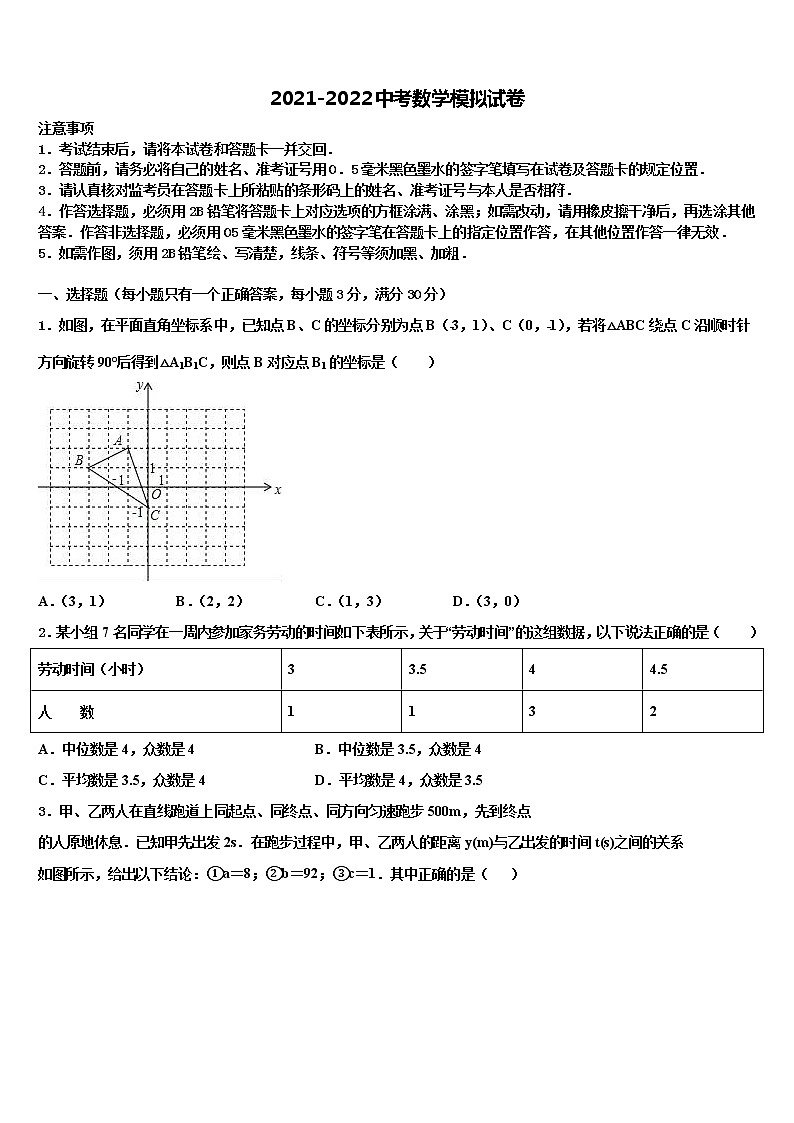
1．如图，在平面直角坐标系中，已知点B、C的坐标分别为点B（﹣3，1）、C（0，﹣1），若将△ABC绕点C沿顺时针方向旋转90°后得到△A1B1C，则点B对应点B1的坐标是（　　）

A．（3，1） B．（2，2） C．（1，3） D．（3，0）
2．某小组7名同学在一周内参加家务劳动的时间如下表所示，关于“劳动时间”的这组数据，以下说法正确的是（　　）
劳动时间（小时）
3
3.5
4
4.5
人　　数
1
1
3
2
A．中位数是4，众数是4 B．中位数是3.5，众数是4
C．平均数是3.5，众数是4 D．平均数是4，众数是3.5
3．甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m，先到终点
的人原地休息．已知甲先出发2s．在跑步过程中，甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系
如图所示，给出以下结论：①a＝8；②b＝92；③c＝1．其中正确的是（ ）

A．①②③ B．仅有①② C．仅有①③ D．仅有②③
4．在平面直角坐标系中，若点A(a，－b)在第一象限内，则点B(a，b)所在的象限是(　　)
A．第一象限 B．第二象限 C．第三象限 D．第四象限
5．一个容量为50的样本,在整理频率分布时,将所有频率相加,其和是( )
A．50 B．0.02 C．0.1 D．1
6．从标号分别为1，2，3，4，5的5张卡片中随机抽取1张，下列事件中不可能事件是（　　）
A．标号是2 B．标号小于6 C．标号为6 D．标号为偶数
7．甲、乙两辆汽车沿同一路线从A地前往B地，甲车以a千米/时的速度匀速行驶，途中出现故障后停车维修，修好后以2a千米/时的速度继续行驶；乙车在甲车出发2小时后匀速前往B地，比甲车早30分钟到达．到达B地后，乙车按原速度返回A地，甲车以2a千米/时的速度返回A地．设甲、乙两车与A地相距s（千米），甲车离开A地的时间为t（小时），s与t之间的函数图象如图所示．下列说法：①a=40；②甲车维修所用时间为1小时；③两车在途中第二次相遇时t的值为5.25；④当t=3时，两车相距40千米，其中不正确的个数为（　　）

A．0个 B．1个 C．2个 D．3个
8．如图，在▱ABCD中，∠DAB的平分线交CD于点E，交BC的延长线于点G，∠ABC的平分线交CD于点F，交AD的延长线于点H，AG与BH交于点O，连接BE，下列结论错误的是（　　）

A．BO=OH B．DF=CE C．DH=CG D．AB=AE
9．将抛物线向左平移1个单位，再向下平移3个单位后所得抛物线的解析式为（ ）
A． B． C． D．
10．如图，平行于x轴的直线与函数，的图象分别相交于A，B两点，点A在点B的右侧，C为x轴上的一个动点，若的面积为4，则的值为　　

A．8 B． C．4 D．
二、填空题（共7小题，每小题3分，满分21分）
11．如图，矩形OABC的边OA，OC分别在轴、轴上，点B在第一象限，点D在边BC上，且∠AOD=30°，四边形OA′B′D与四边形OABD关于直线OD对称（点A′和A，B′和B分别对应），若AB=1，反比例函数的图象恰好经过点A′，B，则的值为_________．

12．化简：+3=_____．
13．大型纪录片《厉害了，我的国》上映25天，累计票房约为402700000元，成为中国纪录电影票房冠军．402700000用科学记数法表示是________．
14．如图，转盘中6个扇形的面积相等，任意转动转盘1次，当转盘停止转动时，指针指向的数小于5的概率为_____．

15．我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 　尺. 

16．如图，在直角三角形ABC中，∠ACB=90°，CA=4，点P是半圆弧AC的中点，连接BP，线段即把图形APCB（指半圆和三角形ABC组成的图形）分成两部分，则这两部分面积之差的绝对值是_____．

17．已知抛物线y＝－x2＋mx＋2－m，在自变量x的值满足－1≤x≤2的情况下．若对应的函数值y的最大值为6，则m的值为__________.
三、解答题（共7小题，满分69分）
18．（10分）先化简，再求值：，其中满足．
19．（5分）小李在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考，请你帮他完成如下问题：
他认为该定理有逆定理：“如果一个三角形某条边上的中线等于该边长的一半，那么这个三角形是直角三角形”应该成立.即如图①，在中，是边上的中线，若，求证：.如图②，已知矩形，如果在矩形外存在一点，使得，求证：.（可以直接用第（1）问的结论）在第（2）问的条件下，如果恰好是等边三角形，请求出此时矩形的两条邻边与的数量关系.
20．（8分）如图，△ABD是⊙O的内接三角形，E是弦BD的中点，点C是⊙O外一点且∠DBC＝∠A，连接OE延长与圆相交于点F，与BC相交于点C．求证：BC是⊙O的切线；若⊙O的半径为6，BC＝8，求弦BD的长．

21．（10分）为了解今年初三学生的数学学习情况，某校对上学期的数学成绩作了统计分析，绘制得到如下图表．请结合图表所给出的信息解答下列问题：
成绩
频数
频率
优秀
45
b
良好
a
0.3
合格
105
0.35
不合格
60
c
（1）该校初三学生共有多少人？求表中a，b，c的值，并补全条形统计图．初三（一）班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍，求恰好选中甲、乙两位同学的概率．

22．（10分）我们知道中，如果，，那么当时，的面积最大为6；
(1)若四边形中，，且，直接写出满足什么位置关系时四边形面积最大？并直接写出最大面积.
(2)已知四边形中，，求为多少时，四边形面积最大？并求出最大面积是多少？
23．（12分）如图，已知点A（1，a）是反比例函数y1=的图象上一点，直线y2=﹣与反比例函数y1=的图象的交点为点B、D，且B（3，﹣1），求：
（Ⅰ）求反比例函数的解析式；
（Ⅱ）求点D坐标，并直接写出y1＞y2时x的取值范围；
（Ⅲ）动点P（x，0）在x轴的正半轴上运动，当线段PA与线段PB之差达到最大时，求点P的坐标．

24．（14分）如图，六个完全相同的小长方形拼成了一个大长方形，AB是其中一个小长方形的对角线，请在大长方形中完成下列画图，要求：①仅用无刻度直尺，②保留必要的画图痕迹．
在图1中画出一个45°角，使点A或点B是这个角的顶点，且AB为这个角的一边；在图2中画出线段AB的垂直平分线．



参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1、B
【解析】
作出点A、B绕点C按顺时针方向旋转90°后得到的对应点，再顺次连接可得△A1B1C，即可得到点B对应点B1的坐标．
【详解】
解：如图所示，△A1B1C即为旋转后的三角形，点B对应点B1的坐标为（2，2）．

故选：B．
【点睛】
此题主要考查了平移变换和旋转变换，正确根据题意得出对应点位置是解题关键． 图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．
2、A
【解析】
根据众数和中位数的概念求解．
【详解】
这组数据中4出现的次数最多，众数为4，
∵共有7个人，
∴第4个人的劳动时间为中位数，
所以中位数为4，
故选A．
【点睛】
本题考查众数与中位数的意义，一组数据中出现次数最多的数据叫做众数；中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．
3、A
【解析】
解：∵乙出发时甲行了2秒，相距8m，∴甲的速度为8/2＝4m/ s．
∵100秒时乙开始休息．∴乙的速度是500/100＝5m/ s．
∵a秒后甲乙相遇，∴a＝8/(5－4)＝8秒．因此①正确．
∵100秒时乙到达终点，甲走了4×(100＋2)＝408 m，∴b＝500－408＝92 m． 因此②正确．
∵甲走到终点一共需耗时500/4＝125 s，，∴c＝125－2＝1 s． 因此③正确．
终上所述，①②③结论皆正确．故选A．
4、D
【解析】
先根据第一象限内的点的坐标特征判断出a、b的符号，进而判断点B所在的象限即可.
【详解】
∵点A(a，-b)在第一象限内，
∴a>0，-b>0，
∴b<0，
∴点B((a，b)在第四象限，
故选D．
【点睛】
本题考查了点的坐标，解决本题的关键是牢记平面直角坐标系中各个象限内点的符号特征：第一象限正正，第二象限负正，第三象限负负，第四象限正负．
5、D
【解析】
所有小组频数之和等于数据总数，所有频率相加等于1.
6、C
【解析】
利用随机事件以及必然事件和不可能事件的定义依次分析即可解答．
【详解】
选项A、标号是2是随机事件；
选项B、该卡标号小于6是必然事件；
选项C、标号为6是不可能事件；
选项D、该卡标号是偶数是随机事件；
故选C．
【点睛】
本题考查了随机事件以及必然事件和不可能事件的定义，正确把握相关定义是解题关键．
7、A
【解析】
解：①由函数图象，得a=120÷3=40，
故①正确，
②由题意，得5.5﹣3﹣120÷（40×2），
=2.5﹣1.5，
=1．
∴甲车维修的时间为1小时；
故②正确，
③如图：

∵甲车维修的时间是1小时，
∴B（4，120）．
∵乙在甲出发2小时后匀速前往B地，比甲早30分钟到达．
∴E（5，240）．
∴乙行驶的速度为：240÷3=80，
∴乙返回的时间为：240÷80=3，
∴F（8，0）．
设BC的解析式为y1=k1t+b1，EF的解析式为y2=k2t+b2，由图象得，
，，
解得，，
∴y1=80t﹣200，y2=﹣80t+640，
当y1=y2时，
80t﹣200=﹣80t+640，
t=5.2．
∴两车在途中第二次相遇时t的值为5.2小时，
故弄③正确，
④当t=3时，甲车行的路程为：120km，乙车行的路程为：80×（3﹣2）=80km，
∴两车相距的路程为：120﹣80=40千米，
故④正确，
故选A．
8、D
【解析】
解：∵四边形ABCD是平行四边形，∴AH∥BG，AD=BC，∴∠H=∠HBG．∵∠HBG=∠HBA，∴∠H=∠HBA，∴AH=AB．
同理可证BG=AB，∴AH=BG．∵AD=BC，∴DH=CG，故C正确．
∵AH=AB，∠OAH=∠OAB，∴OH=OB，故A正确．
∵DF∥AB，∴∠DFH=∠ABH．∵∠H=∠ABH，∴∠H=∠DFH，∴DF=DH．
同理可证EC=CG．
∵DH=CG，∴DF=CE，故B正确．
无法证明AE=AB，故选D．
9、D
【解析】
根据“左加右减、上加下减”的原则，
将抛物线向左平移1个单位所得直线解析式为：；
再向下平移3个单位为：．故选D．
10、A
【解析】
【分析】设，，根据反比例函数图象上点的坐标特征得出，根据三角形的面积公式得到，即可求出．
【详解】轴，
，B两点纵坐标相同，
设，，则，，
，
，
故选A．
【点睛】本题考查了反比例函数图象上点的坐标特征，三角形的面积，熟知点在函数的图象上，则点的坐标满足函数的解析式是解题的关键.

二、填空题（共7小题，每小题3分，满分21分）
11、
【解析】
解：∵四边形ABCO是矩形，AB=1，
∴设B（m，1），
∴OA=BC=m，
∵四边形OA′B′D与四边形OABD关于直线OD对称，
∴OA′=OA=m，∠A′OD=∠AOD=30°，
∴∠A′OA=60°，
过A′作A′E⊥OA于E，
∴OE=m，A′E=m，
∴A′（m，m），
∵反比例函数y=（k≠0）的图象恰好经过点A′，B，
∴m•m=m，
∴m=，
∴k=．

【点睛】
本题考查反比例函数图象上点的坐标特征；矩形的性质，利用数形结合思想解题是关键．
12、
【解析】
试题分析：先进行二次根式的化简，然后合并，可得原式=2+=3．
13、4.027
【解析】
分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．
详解：4 0270 0000用科学记数法表示是4.027×1．
故答案为4.027×1．
点睛：本题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
14、
【解析】
试题解析：∵共6个数，小于5的有4个，∴P（小于5）==．故答案为．
15、1.
【解析】
试题分析：这种立体图形求最短路径问题，可以展开成为平面内的问题解决，展开后可转化下图，所以是直角三角形求斜边的问题，根据勾股定理可求出葛藤长为=1（尺）．
故答案为1．

考点：平面展开最短路径问题
16、4
【解析】
连接把两部分的面积均可转化为规则图形的面积，不难发现两部分面积之差的绝对值即为的面积的2倍．
【详解】
解：连接OP、OB，

∵图形BAP的面积=△AOB的面积+△BOP的面积+扇形OAP的面积，
图形BCP的面积=△BOC的面积+扇形OCP的面积−△BOP的面积，
又∵点P是半圆弧AC的中点，OA=OC，
∴扇形OAP的面积=扇形OCP的面积，△AOB的面积=△BOC的面积，
∴两部分面积之差的绝对值是
点睛：考查扇形面积和三角形的面积，把不规则图形的面积转化为规则图形的面积是解题的关键.
17、m=8或
【解析】
求出抛物线的对称轴分三种情况进行讨论即可.
【详解】
抛物线的对称轴，抛物线开口向下，
当，即时，抛物线在－1≤x≤2时，随的增大而减小，在时取得最大值，即 解得符合题意.
当即时，抛物线在－1≤x≤2时，在时取得最大值，即 无解.
当,即时，抛物线在－1≤x≤2时，随的增大而增大，在时取得最大值，即 解得符合题意.
综上所述，m的值为8或
故答案为：8或
【点睛】
考查二次函数的图象与性质，注意分类讨论，不要漏解.

三、解答题（共7小题，满分69分）
18、，1．
【解析】
原式括号中的两项通分并利用同分母分式的加法法则计算，再与括号外的分式通分后利用同分母分式的加法法则计算，约分得到最简结果，将变形为，整体代入计算即可．
【详解】
解：原式





∵，
∴，
∴原式
【点睛】
本题主要考查分式的化简求值，解题的关键是掌握分式的混合运算顺序和运算法则．
19、（1）详见解析；（2）详见解析；（3）
【解析】
（1）利用等腰三角形的性质和三角形内角和即可得出结论；
（2）先判断出OE=AC，即可得出OE=BD，即可得出结论；
（3）先判断出△ABE是底角是30°的等腰三角形，即可构造直角三角形即可得出结论．
【详解】
（1）∵AD=BD，
∴∠B=∠BAD，
∵AD=CD，
∴∠C=∠CAD，
在△ABC中，∠B+∠C+∠BAC=180°，
∴∠B+∠C+∠BAD+∠CAD=∠B+∠C+∠B+∠C=180°
∴∠B+∠C=90°，
∴∠BAC=90°，
（2）如图②，连接与，交点为，连接

四边形是矩形







（3）如图3，过点做于点

四边形是矩形
，
是等边三角形
，
由（2）知，


在中，
，



【点睛】
此题是四边形综合题，主要考查了矩形是性质，直角三角形的性质和判定，含30°角的直角三角形的性质，三角形的内角和公式，解（1）的关键是判断出∠B=∠BAD，解（2）的关键是判断出OE=AC，解（3）的关键是判断出△ABE是底角为30°的等腰三角形，进而构造直角三角形．
20、（1）详见解析；（2）BD=9.6.
【解析】
试题分析：(1)连接OB，由垂径定理可得BE=DE，OE⊥BD， ，再由圆周角定理可得 ，从而得到∠ OBE＋∠ DBC＝90°，即 ，命题得证.
(2)由勾股定理求出OC，再由△OBC的面积求出BE，即可得出弦BD的长.
试题解析：(1)证明：如下图所示，连接OB.
∵ E是弦BD的中点，∴ BE＝DE，OE⊥ BD，，
∴∠ BOE＝∠ A，∠ OBE＋∠ BOE＝90°.
∵∠ DBC＝∠ A，∴∠ BOE＝∠ DBC，
∴∠ OBE＋∠ DBC＝90°，∴∠ OBC＝90°，即BC⊥OB，∴ BC是⊙ O的切线．

(2)解：∵ OB＝6，BC＝8，BC⊥OB，∴ ,
∵ ，∴ ，
∴.
点睛：本题主要考查圆中的计算问题，解题的关键在于清楚角度的转换方式和弦长的计算方法.
21、（1）300人（2）b=0.15，c=0.2；（3）
【解析】
分析：(1)利用合格的人数除以该组频率进而得出该校初四学生总数;
(2)利用(1)中所求,结合频数÷总数=频率,进而求出答案;
(3)根据题意画出树状图,然后求得全部情况的总数与符合条件的情况数目;二者的比值就是其发生的概率.
详解：（1）由题意可得：该校初三学生共有：105÷0.35=300（人），
答：该校初三学生共有300人；
（2）由（1）得：a=300×0.3=90（人），
b==0.15，
c==0.2；
如图所示：

（3）画树形图得：

∵一共有12种情况，抽取到甲和乙的有2种，
∴P（抽到甲和乙）==．
点睛：此题主要考查了树状图法求概率以及条形统计图的应用,根据题意利用树状图得出所有情况是解题关键.
22、 (1)当，时有最大值1；(2)当时，面积有最大值32.
【解析】
（1）由题意当AD∥BC，BD⊥AD时，四边形ABCD的面积最大，由此即可解决问题．
（2）设BD=x，由题意：当AD∥BC，BD⊥AD时，四边形ABCD的面积最大，构建二次函数，利用二次函数的性质即可解决问题．
【详解】
(1) 由题意当AD∥BC，BD⊥AD时，四边形ABCD的面积最大，
最大面积为×6×（16-6）=1．
故当，时有最大值1；
(2)当，时有最大值，
设, 由题意：当AD∥BC，BD⊥AD时，四边形ABCD的面积最大，








∴抛物线开口向下
∴当 时，面积有最大值32.
【点睛】
本题考查三角形的面积，二次函数的应用等知识，解题的关键是学会利用参数构建二次函数解决问题．
23、（1）反比例函数的解析式为y=﹣；（2）D（﹣2，）；﹣2＜x＜0或x＞3；（3）P（4，0）．
【解析】
试题分析：（1）把点B（3，﹣1）带入反比例函数中，即可求得k的值；
（2）联立直线和反比例函数的解析式构成方程组，化简为一个一元二次方程，解方程即可得到点D坐标，观察图象可得相应x的取值范围；
（3）把A（1，a）是反比例函数的解析式，求得a的值，可得点A坐标，用待定系数法求得直线AB的解析式，令y=0，解得x的值，即可求得点P的坐标.
试题解析：（1）∵B（3，﹣1）在反比例函数的图象上，
∴-1=，
∴m=-3，
∴反比例函数的解析式为；
（2），
∴=，
x2-x-6=0，
（x-3）（x+2）=0，
x1=3，x2=-2，
当x=-2时，y=，
∴D（－2，）；
y1＞y2时x的取值范围是-2；
（3）∵A（1，a）是反比例函数的图象上一点，
∴a=-3，
∴A（1，-3），
设直线AB为y=kx+b,
，
∴，
∴直线AB为y=x-4，
令y=0，则x=4，
∴P(4，0)
24、（1）答案见解析；（2）答案见解析．
【解析】
试题分析：（1）根据等腰直角三角形的性质即可解决问题．
（2）根据正方形、长方形的性质对角线相等且互相平分，即可解决问题．
试题解析：（1）如图所示，∠ABC=45°．（AB、AC是小长方形的对角线）．

（2）线段AB的垂直平分线如图所示，点M是长方形AFBE是对角线交点，点N是正方形ABCD的对角线的交点，直线MN就是所求的线段AB的垂直平分线．

考点：作图—应用与设计作图．