2021-2022学年山西农业大学附属学校中考数学模拟精编试卷含解析

这是一份2021-2022学年山西农业大学附属学校中考数学模拟精编试卷含解析，共22页。
2021-2022中考数学模拟试卷
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．如图，直线AB∥CD，∠C＝44°，∠E为直角，则∠1等于（　　）

A．132° B．134° C．136° D．138°
2．对于不为零的两个实数a，b，如果规定：a★b＝，那么函数y＝2★x的图象大致是（　　）
A． B． C． D．
3．如果关于x的方程x2﹣x+1=0有实数根，那么k的取值范围是（　　）
A．k＞0 B．k≥0 C．k＞4 D．k≥4
4．如图，已知四边形ABCD，R，P分别是DC，BC上的点，E，F分别是AP，RP的中点，当点P在BC上从点B向点C移动而点R不动时， 那么下列结论成立的是（ ）．

A．线段EF的长逐渐增大 B．线段EF的长逐渐减少
C．线段EF的长不变 D．线段EF的长不能确定
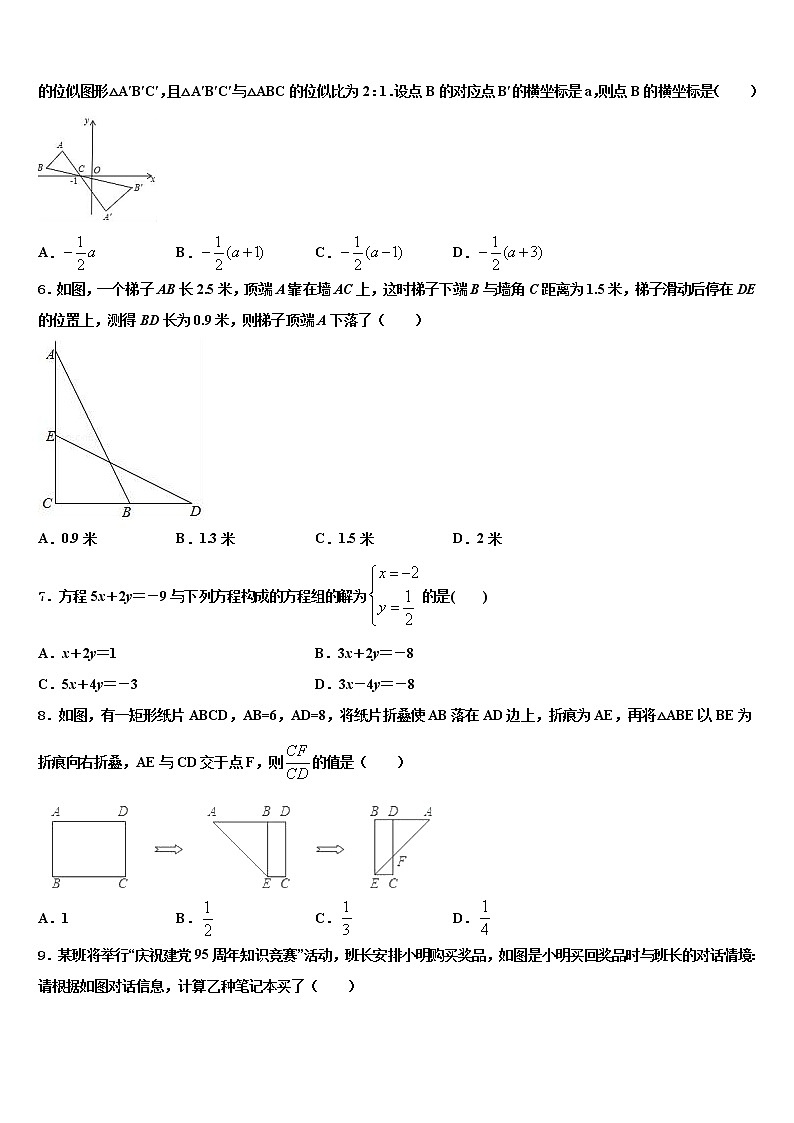
5．如图，△ABC中AB两个顶点在x轴的上方，点C的坐标是（﹣1，0），以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C′，且△A′B′C′与△ABC的位似比为2：1．设点B的对应点B′的横坐标是a，则点B的横坐标是（　　）

A． B． C． D．
6．如图，一个梯子AB长2.5米，顶端A靠在墙AC上，这时梯子下端B与墙角C距离为1.5米，梯子滑动后停在DE的位置上，测得BD长为0.9米，则梯子顶端A下落了（　　）

A．0.9米 B．1.3米 C．1.5米 D．2米
7．方程5x＋2y＝－9与下列方程构成的方程组的解为的是(　　)
A．x＋2y＝1 B．3x＋2y＝－8
C．5x＋4y＝－3 D．3x－4y＝－8
8．如图，有一矩形纸片ABCD，AB=6，AD=8，将纸片折叠使AB落在AD边上，折痕为AE，再将△ABE以BE为折痕向右折叠，AE与CD交于点F，则的值是（　　）

A．1 B． C． D．
9．某班将举行“庆祝建党95周年知识竞赛”活动，班长安排小明购买奖品，如图是小明买回奖品时与班长的对话情境：请根据如图对话信息，计算乙种笔记本买了（　　）

A．25本 B．20本 C．15本 D．10本
10．《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何？”．意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等．两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）．问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，根据题意得（　　）
A．
B．
C．
D．
11．我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”．如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是（　　）

A．84 B．336 C．510 D．1326
12．如图，平面直角坐标系中，矩形ABCD的边AB：BC＝3：2，点A（3，0），B（0，6）分别在x轴，y轴上，反比例函数y＝的图象经过点D，则k值为（　　）

A．﹣14 B．14 C．7 D．﹣7
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．规定：[x]表示不大于x的最大整数，（x）表示不小于x的最小整数，[x）表示最接近x的整数（x≠n+0.5，n为整数），例如：[1.3]=1，（1.3）=3，[1.3）=1．则下列说法正确的是________．（写出所有正确说法的序号）
①当x=1.7时，[x]+（x）+[x）=6；
②当x=﹣1.1时，[x]+（x）+[x）=﹣7；
③方程4[x]+3（x）+[x）=11的解为1＜x＜1.5；
④当﹣1＜x＜1时，函数y=[x]+（x）+x的图象与正比例函数y=4x的图象有两个交点．
14．如图，把正方形铁片OABC置于平面直角坐标系中，顶点A的坐标为（3，0），点P（1，2）在正方形铁片上，将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°，第一次旋转至图①位置，第二次旋转至图②位置…，则正方形铁片连续旋转2017次后，点P的坐标为____________________．

15．如图，中，，，，，平分，与相交于点，则的长等于_____.

16．已知扇形的圆心角为120°，弧长为6π，则扇形的面积是_____．
17．的系数是_____，次数是_____．
18．在如图所示（A，B，C三个区域）的图形中随机地撒一把豆子，豆子落在 区域的可能性最大（填A或B或C）．

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19．（6分）如图，在矩形ABCD中，AB=1DA，以点A为圆心，AB为半径的圆弧交DC于点E，交AD的延长线于点F，设DA=1．求线段EC的长；求图中阴影部分的面积．

20．（6分）（1）如图1，正方形ABCD中，点E，F分别在边CD，AD上，AE⊥BF于点G，求证：AE=BF；
（2）如图2，矩形ABCD中，AB=2，BC=3，点E，F分别在边CD，AD上，AE⊥BF于点M，探究AE与BF的数量关系，并证明你的结论；
（3）在（2）的基础上，若AB=m，BC=n，其他条件不变，请直接写出AE与BF的数量关系；　 　．

21．（6分）观察下列各式：
①
②
③
由此归纳出一般规律__________.
22．（8分）图1是一辆吊车的实物图，图2是其工作示意图，AC是可以伸缩的起重臂，其转动点A离地面BD的高度AH为3.4m．当起重臂AC长度为9m，张角∠HAC为118°时，求操作平台C离地面的高度（结果保留小数点后一位：参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）

23．（8分）如图，已知一次函数的图象与反比例函数的图象交于点，与轴、轴交于两点，过作垂直于轴于点.已知.
（1）求一次函数和反比例函数的表达式；
（2）观察图象:当时，比较.

24．（10分）解方程组：.
25．（10分）如图，M、N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞.工程人员为了计算工程量，必须计算M、N两点之间的直线距离，选择测量点A、B、C，点B、C分别在AM、AN上，现测得AM=1千米、AN=1.8千米，AB=54米、BC=45米、AC=30米，求M、N两点之间的距离.

26．（12分）如图，将平行四边形ABCD纸片沿EF折叠，使点C与点A重合，点D落在点G处．
(1)连接CF，求证：四边形AECF是菱形；
(2)若E为BC中点，BC＝26，tan∠B＝，求EF的长．

27．（12分）在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元.求每台电脑、每台电子白板各多少万元?根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低.



参考答案

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1、B
【解析】
过E作EF∥AB，求出AB∥CD∥EF，根据平行线的性质得出∠C=∠FEC，∠BAE=∠FEA，求出∠BAE，即可求出答案．
解：

过E作EF∥AB，
∵AB∥CD，
∴AB∥CD∥EF，
∴∠C=∠FEC，∠BAE=∠FEA，
∵∠C=44°，∠AEC为直角，
∴∠FEC=44°，∠BAE=∠AEF=90°﹣44°=46°，
∴∠1=180°﹣∠BAE=180°﹣46°=134°，
故选B．
“点睛”本题考查了平行线的性质的应用，能正确作出辅助线是解此题的关键．
2、C
【解析】
先根据规定得出函数y＝2★x的解析式，再利用一次函数与反比例函数的图象性质即可求解．
【详解】
由题意，可得当2＜x，即x＞2时，y＝2+x，y是x的一次函数，图象是一条射线除去端点，故A、D错误；
当2≥x，即x≤2时，y＝﹣，y是x的反比例函数，图象是双曲线，分布在第二、四象限，其中在第四象限时，0＜x≤2，故B错误．
故选：C．
【点睛】
本题考查了新定义，函数的图象，一次函数与反比例函数的图象性质，根据新定义得出函数y＝2★x的解析式是解题的关键．
3、D
【解析】
由被开方数非负结合根的判别式△≥0，即可得出关于k的一元一次不等式组，解之即可得出k的取值范围．
【详解】
∵关于x的方程x2-x+1=0有实数根，
∴，
解得：k≥1．
故选D．
【点睛】
本题考查了根的判别式，牢记“当△≥0时，方程有实数根”是解题的关键．
4、C
【解析】
因为R不动，所以AR不变．根据三角形中位线定理可得EF= AR，因此线段EF的长不变．
【详解】
如图，连接AR，

∵E、F分别是AP、RP的中点，
∴EF为△APR的中位线，
∴EF= AR，为定值．
∴线段EF的长不改变．
故选：C．
【点睛】
本题考查了三角形的中位线定理，只要三角形的边AR不变，则对应的中位线的长度就不变．
5、D
【解析】
设点B的横坐标为x，然后表示出BC、B′C的横坐标的距离，再根据位似变换的概念列式计算．
【详解】
设点B的横坐标为x，则B、C间的横坐标的长度为﹣1﹣x，B′、C间的横坐标的长度为a+1，
∵△ABC放大到原来的2倍得到△A′B′C，
∴2（﹣1﹣x）＝a+1，
解得x＝﹣（a+3），
故选：D．
【点睛】
本题考查了位似变换，坐标与图形的性质，根据位似变换的定义，利用两点间的横坐标的距离等于对应边的比列出方程是解题的关键．
6、B
【解析】
试题分析：要求下滑的距离，显然需要分别放到两个直角三角形中，运用勾股定理求得AC和CE的长即可．
解：在Rt△ACB中，AC2=AB2﹣BC2=2.52﹣1.52=1，
∴AC=2，
∵BD=0.9，
∴CD=2.1．
在Rt△ECD中，EC2=ED2﹣CD2=2.52﹣2.12=0.19，
∴EC=0.7，
∴AE=AC﹣EC=2﹣0.7=1.2．
故选B．
考点：勾股定理的应用．
7、D
【解析】
试题分析：将x与y的值代入各项检验即可得到结果．
解：方程5x+2y=﹣9与下列方程构成的方程组的解为的是3x﹣4y=﹣1．
故选D．
点评：此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程成立的未知数的值．
8、C
【解析】
由题意知：AB=BE=6，BD=AD﹣AB=2（图2中），AD=AB﹣BD=4（图3中）；
∵CE∥AB，
∴△ECF∽△ADF，
得，
即DF=2CF，所以CF：CD=1：3，
故选C．

【点睛】本题考查了矩形的性质，折叠问题，相似三角形的判定与性质等，准确识图是解题的关键.
9、C
【解析】
设甲种笔记本买了x本，甲种笔记本的单价是y元，则乙种笔记本买了（40﹣x）本，乙种笔记本的单价是（y+3）元，根据题意列出关于x、y的二元一次方程组，求出x、y的值即可．
【详解】
解：设甲种笔记本买了x本，甲种笔记本的单价是y元，则乙种笔记本买了（40﹣x）本，乙种笔记本的单价是（y+3）元，
根据题意，得：，
解得：，
答：甲种笔记本买了25本，乙种笔记本买了15本．
故选C．
【点睛】
本题考查的是二元二次方程组的应用，能根据题意得出关于x、y的二元二次方程组是解答此题的关键．
10、D
【解析】
根据题意可得等量关系：①9枚黄金的重量=11枚白银的重量；②（10枚白银的重量+1枚黄金的重量）-（1枚白银的重量+8枚黄金的重量）=13两，根据等量关系列出方程组即可．
【详解】
设每枚黄金重x两，每枚白银重y两，
由题意得：，
故选：D．
【点睛】
此题主要考查了由实际问题抽象出二元一次方程组，关键是正确理解题意，找出题目中的等量关系．
11、C
【解析】
由题意满七进一，可得该图示为七进制数，化为十进制数为：1×73+3×72+2×7+6=510，
故选：C．
点睛：本题考查记数的方法，注意运用七进制转化为十进制，考查运算能力，属于基础题.
12、B
【解析】
过点D作DF⊥x轴于点F,则∠AOB=∠DFA=90°,∴∠OAB+∠ABO=90°,
∵四边形ABCD是矩形,∴∠BAD=90°,AD=BC,∴∠OAB+∠DAF=90°,∴∠ABO=∠DAF,
∴△AOB∽△DFA,∴OA：DF=OB：AF=AB：AD,
∵AB：BC=3：2,点A（3,0）,B（0,6）,∴AB：AD=3：2,OA=3,OB=6,∴DF=2,AF=4,∴OF=OA+AF=7,∴点D的坐标为:（7,2）,∴k,故选B.

二、填空题：（本大题共6个小题，每小题4分，共24分．）
13、②③
【解析】
试题解析：①当x=1.7时，
[x]+（x）+[x）
=[1.7]+（1.7）+[1.7）=1+1+1=5，故①错误；
②当x=﹣1.1时，
[x]+（x）+[x）
=[﹣1.1]+（﹣1.1）+[﹣1.1）
=（﹣3）+（﹣1）+（﹣1）=﹣7，故②正确；
③当1＜x＜1.5时，
4[x]+3（x）+[x）
=4×1+3×1+1
=4+6+1
=11，故③正确；
④∵﹣1＜x＜1时，
∴当﹣1＜x＜﹣0.5时，y=[x]+（x）+x=﹣1+0+x=x﹣1，
当﹣0.5＜x＜0时，y=[x]+（x）+x=﹣1+0+x=x﹣1，
当x=0时，y=[x]+（x）+x=0+0+0=0，
当0＜x＜0.5时，y=[x]+（x）+x=0+1+x=x+1，
当0.5＜x＜1时，y=[x]+（x）+x=0+1+x=x+1，
∵y=4x，则x﹣1=4x时，得x=；x+1=4x时，得x=；当x=0时，y=4x=0，
∴当﹣1＜x＜1时，函数y=[x]+（x）+x的图象与正比例函数y=4x的图象有三个交点，故④错误，
故答案为②③．
考点：1.两条直线相交或平行问题；1.有理数大小比较；3.解一元一次不等式组．
14、（6053，2）．
【解析】
根据前四次的坐标变化总结规律，从而得解.
【详解】
第一次P1（5，2），第二次P2（8，1），第三次P3（10，1），第四次P4（13，1），第五次P5（17，2），…
发现点P的位置4次一个循环，
∵2017÷4=504余1，
P2017的纵坐标与P1相同为2，横坐标为5+3×2016=6053，
∴P2017（6053，2），
故答案为（6053，2）．
考点：坐标与图形变化﹣旋转；规律型：点的坐标．
15、3
【解析】
如图，延长CE、DE，分别交AB于G、H，由∠BAD=∠ADE=60°可得三角形ADH是等边三角形，根据等腰直角三角形的性质可知CG⊥AB，可求出AG的长，进而可得GH的长，根据含30°角的直角三角形的性质可求出EH的长，根据DE=DH-EH即可得答案.
【详解】
如图，延长CE、DE，分别交AB于G、H，
∵∠BAD=∠ADE=60°，
∴△ADH是等边三角形，
∴DH=AD=AH=5，∠DHA=60°，
∵AC=BC，CE平分∠ACB，∠ACB=90°，
∴AB==8，AG=AB=4，CG⊥AB，
∴GH=AH=AG=5-4=1，
∵∠DHA=60°，
∴∠GEH=30°，
∴EH=2GH=2
∴DE=DH-EH=5=2=3.

故答案为：3
【点睛】
本题考查等边三角形的判定及性质、等腰直角三角形的性质及含30°角的直角三角形的性质，熟记30°角所对的直角边等于斜边的一半的性质并正确作出辅助线是解题关键.
16、27π
【解析】
试题分析：设扇形的半径为r．则，解得r=9，∴扇形的面积==27π．故答案为27π．
考点：扇形面积的计算．
17、 1
【解析】
根据单项式系数及次数的定义进行解答即可．
【详解】
根据单项式系数和次数的定义可知，﹣的系数是，次数是1．
【点睛】
本题考查了单项式，熟知单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数是解题的关键．
18、A
【解析】
试题分析：由题意得：SA＞SB＞SC，
故落在A区域的可能性大
考点: 几何概率

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19、（1）；（1）．
【解析】
（1）根据矩形的性质得出AB=AE=4，进而利用勾股定理得出DE的长，即可得出答案;（1）利用锐角三角函数关系得出∠DAE=60°，进而求出图中阴影部分的面积为：，求出即可．
【详解】
解：（1）∵在矩形ABCD中，AB=1DA，DA=1，
∴AB=AE=4，
∴DE= ，
∴EC=CD-DE=4-1；
（1）∵sin∠DEA= ，
∴∠DEA=30°，
∴∠EAB=30°，
∴图中阴影部分的面积为：
S扇形FAB-S△DAE-S扇形EAB=
．
【点睛】
此题主要考查了扇形的面积计算以及勾股定理和锐角三角函数关系等知识，根据已知得出DE的长是解题关键．
20、（1）证明见解析；（2）AE=BF，（3）AE=BF；
【解析】
（1）根据正方形的性质，可得∠ABC与∠C的关系，AB与BC的关系，根据两直线垂直，可得∠AMB的度数，根据直角三角形锐角的关系，可得∠ABM与∠BAM的关系，根据同角的余角相等，可得∠BAM与∠CBF的关系，根据ASA，可得△ABE≌△BCF，根据全等三角形的性质，可得答案；（2）根据矩形的性质得到∠ABC=∠C，由余角的性质得到∠BAM=∠CBF，根据相似三角形的性质即可得到结论;（3）结论：AE=BF．证明方法类似（2）；
【详解】
（1）证明：

∵四边形ABCD是正方形，
∴∠ABC=∠C，AB=BC．
∵AE⊥BF，
∴∠AMB=∠BAM+∠ABM=90°，
∵∠ABM+∠CBF=90°，
∴∠BAM=∠CBF．
在△ABE和△BCF中，
，
∴△ABE≌△BCF（ASA），
∴AE=BF；
（2）解：如图2中，结论：AE=BF，

理由：∵四边形ABCD是矩形，
∴∠ABC=∠C，
∵AE⊥BF，
∴∠AMB=∠BAM+∠ABM=90°，
∵∠ABM+∠CBF=90°，
∴∠BAM=∠CBF，
∴△ABE∽△BCF，
∴，
∴AE=BF．
（3）结论：AE=BF．
理由：∵四边形ABCD是矩形，
∴∠ABC=∠C，
∵AE⊥BF，
∴∠AMB=∠BAM+∠ABM=90°，
∵∠ABM+∠CBF=90°，
∴∠BAM=∠CBF，
∴△ABE∽△BCF，
∴，
∴AE=BF．
【点睛】
本题考查了四边形综合题、相似三角形的判定和性质，全等三角形的判定和性质，正方形的性质，矩形的性质，熟练掌握全等三角形或相似三角形的判定和性质是解题的关键．
21、xn+1-1
【解析】
试题分析：观察其右边的结果：第一个是﹣1；第二个是﹣1；…依此类推，则第n个的结果即可求得．
试题解析：（x﹣1）（++…x+1）=．
故答案为.
考点：平方差公式．
22、操作平台C离地面的高度为7.6m．
【解析】
分析：作CE⊥BD于F，AF⊥CE于F，如图2，易得四边形AHEF为矩形，则EF=AH=3.4m，∠HAF=90°，再计算出∠CAF=28°，则在Rt△ACF中利用正弦可计算出CF，然后计算CF+EF即可．
详解：作CE⊥BD于F，AF⊥CE于F，如图2，

易得四边形AHEF为矩形，
∴EF=AH=3.4m，∠HAF=90°，
∴∠CAF=∠CAH-∠HAF=118°-90°=28°，
在Rt△ACF中，∵sin∠CAF=，
∴CF=9sin28°=9×0.47=4.23，
∴CE=CF+EF=4.23+3.4≈7.6（m），
答：操作平台C离地面的高度为7.6m．
点睛：本题考查了解直角三角形的应用：先将实际问题抽象为数学问题（画出平面图形，构造出直角三角形转化为解直角三角形问题），然后利用勾股定理和三角函数的定义进行几何计算．
23、（1）;（2）
【解析】
（1）由一次函数的解析式可得出D点坐标，从而得出OD长度，再由△ODC与△BAC相似及AB与BC的长度得出C、B、A的坐标，进而算出一次函数与反比例函数的解析式；
（2）以A点为分界点，直接观察函数图象的高低即可知道答案．
【详解】
解：（1）对于一次函数y=kx-2，令x=0，则y=-2，即D（0，-2），
∴OD=2，
∵AB⊥x轴于B，
∴ ，
∵AB=1，BC=2，
∴OC=4，OB=6，
∴C（4，0），A（6，1）
将C点坐标代入y=kx-2得4k-2=0，
∴k=，
∴一次函数解析式为y=x-2；
将A点坐标代入反比例函数解析式得m=6，
∴反比例函数解析式为y=；
（2）由函数图象可知：
当0＜x＜6时，y1＜y2；
当x=6时，y1=y2；
当x＞6时，y1＞y2；
【点睛】
本题考查了反比例函数与一次函数的交点问题．熟悉函数图象上点的坐标特征和待定系数法解函数解析式的方法是解答本题的关键，同时注意对数形结合思想的认识和掌握．
24、；；.
【解析】
分析：
把原方程组中的第二个方程通过分解因式降次，转化为两个一次方程，再分别和第一方程组合成两个新的方程组，分别解这两个新的方程组即可求得原方程组的解.
详解：
由方程可得，，；
则原方程组转化为（Ⅰ）或 （Ⅱ），
解方程组（Ⅰ）得，
解方程组（Ⅱ）得 ，
∴原方程组的解是 .
点睛：本题考查的是二元二次方程组的解法，解题的要点有两点：（1）把原方程组中的第2个方程通过分解因式降次转化为两个二元一次方程，并分别和第1个方程组合成两个新的方程组；（2）将两个新的方程组消去y，即可得到关于x的一元二次方程.
25、1.5千米
【解析】
先根据相似三角形的判定得出△ABC∽△AMN,再利用相似三角形的性质解答即可
【详解】
在△ABC与△AMN中，，，
∴，
∵∠A=∠A，
∴△ABC∽△ANM，
∴，即，解得MN=1.5(千米) ，
因此，M、N两点之间的直线距离是1.5千米.
【点睛】
此题考查相似三角形的应用，解题关键在于掌握运算法则
26、 (1)证明见解析；(2)EF＝1．
【解析】
(1)如图1，利用折叠性质得EA＝EC，∠1＝∠2，再证明∠1＝∠3得到AE＝AF，则可判断四边形AECF为平行四边形，从而得到四边形AECF为菱形；
(2)作EH⊥AB于H，如图，利用四边形AECF为菱形得到AE＝AF＝CE＝13，则判断四边形ABEF为平行四边形得到EF＝AB，根据等腰三角形的性质得AH＝BH，再在Rt△BEH中利用tanB＝＝可计算出BH＝5，从而得到EF＝AB＝2BH＝1．
【详解】
(1)证明：如图1，
∵平行四边形ABCD纸片沿EF折叠，使点C与点A重合，点D落在点G处，
∴EA＝EC，∠1＝∠2，
∵四边形ABCD为平行四边形，
∴AD∥BC，
∴∠2＝∠3，
∴∠1＝∠3，
∴AE＝AF，
∴AF＝CE，
而AF∥CE，
∴四边形AECF为平行四边形，
∵EA＝EC，
∴四边形AECF为菱形；
(2)解：作EH⊥AB于H，如图，
∵E为BC中点，BC＝26，
∴BE＝EC＝13，
∵四边形AECF为菱形，
∴AE＝AF＝CE＝13，
∴AF＝BE，
∴四边形ABEF为平行四边形，
∴EF＝AB，
∵EA＝EB，EH⊥AB，
∴AH＝BH，
在Rt△BEH中，tanB＝＝，
设EH＝12x，BH＝5x，则BE＝13x，
∴13x＝13，解得x＝1，
∴BH＝5，
∴AB＝2BH＝1，
∴EF＝1．

【点睛】
本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了平行四边形的性质、菱形的判定与性质．
27、（1）每台电脑0.5万元，每台电子白板1.5万元（2）见解析
【解析】
解：（1）设每台电脑x万元，每台电子白板y万元，根据题意得：
，解得：。
答：每台电脑0.5万元，每台电子白板1.5万元。
（2）设需购进电脑a台，则购进电子白板（30－a）台，
则，解得：，即a=15，16，17。
故共有三种方案：
方案一：购进电脑15台，电子白板15台.总费用为万元；
方案二：购进电脑16台，电子白板14台.总费用为万元；
方案三：购进电脑17台，电子白板13台．总费用为万元。
∴方案三费用最低。
（1）设电脑、电子白板的价格分别为x,y元，根据等量关系：“1台电脑+2台电子白板=3.5万元”，“2台电脑+1台电子白板=2.5万元”，列方程组求解即可。
（2）设计方案题一般是根据题意列出不等式组，求不等式组的整数解。设购进电脑x台，电子白板有(30－x)台，然后根据题目中的不等关系“总费用不超过30万元，但不低于28万元”列不等式组解答。