

2022年吉林省中考数学专题练5-二次函数
展开
这是一份2022年吉林省中考数学专题练5-二次函数,共36页。
A.y3<y2<y1B.y2<y1<y3C.y3<y1<y2D.y1<y2<y3
2.(2022•吉林模拟)顶点为(﹣2,1),且开口方向、形状与函数y=﹣2x2的图象相同的抛物线是( )
A.y=﹣2(x﹣2)2﹣1B.y=2(x+2)2+1
C.y=﹣2(x+2)2﹣1D.y=﹣2(x+2)2+1
3.(2021•双阳区二模)如图,在平面直角坐标系中,抛物线y=﹣x2+4x+m的顶点为A,它与x轴分别交于B,C两点,与y轴的交点为D,过点D作DE平行于x轴交抛物线于点E,BF∥CE交DE于点F,若3S△ABC=4S△FEC,则m的值为( )
A.−127B.−712C.﹣12D.12
4.(2021•南关区一模)如图,在平面直角坐标系中,抛物线y=ax2﹣2ax+2(a<0)交x轴正半轴于点A,交y轴于点B,线段BC⊥y轴交此抛物线于点D,且CD=13BC,则△ABC的面积是( )
A.6B.5C.4D.3
5.(2020•双阳区二模)已知二次函数y=﹣(x﹣k)2(k为常数),当自变量x的值满足1≤x≤6时,与其对应的函数值y的最大值为﹣1,则k的值为( )
A.0或5B.5或7C.0或7D.2或5
6.(2020•长春三模)在平面直角坐标系中,若函数y=(k﹣2)x2﹣2kx+k的图象与坐标轴共有三个交点,则下列各数中可能的k值为( )
A.﹣1B.0C.1D.2
7.(2020•吉林二模)将抛物线y=2x2﹣1先向左平移1个单位长度,再向上平移2个单位长度,得到的抛物线的顶点坐标为( )
A.(0,﹣1)B.(1,1)C.(﹣1,﹣3)D.(﹣1,1)
8.(2020•长春模拟)某广场有一个小型喷泉,水流从垂直于地面的水管OA喷出,OA长为1.5m.水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为3m.建立平面直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间近似满足函数关系y=ax2+x+c(a≠0),则水流喷出的最大高度为( )
A.1米B.32米C.2米D.138米
二.填空题(共12小题)
9.(2021•长春)如图,在平面直角坐标系中,点A(2,4)在抛物线y=ax2上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为 .
10.(2022•南关区校级一模)在平面直角坐标系中,二次函数y=﹣x2+mx+3过点(4,3),着当0≤x≤a时,y有最大值7,最小值3,则a的取值范围是 .
11.(2022•吉林模拟)已知二次函数y=(x﹣1)2+3,当x= 时,y取得最小值.
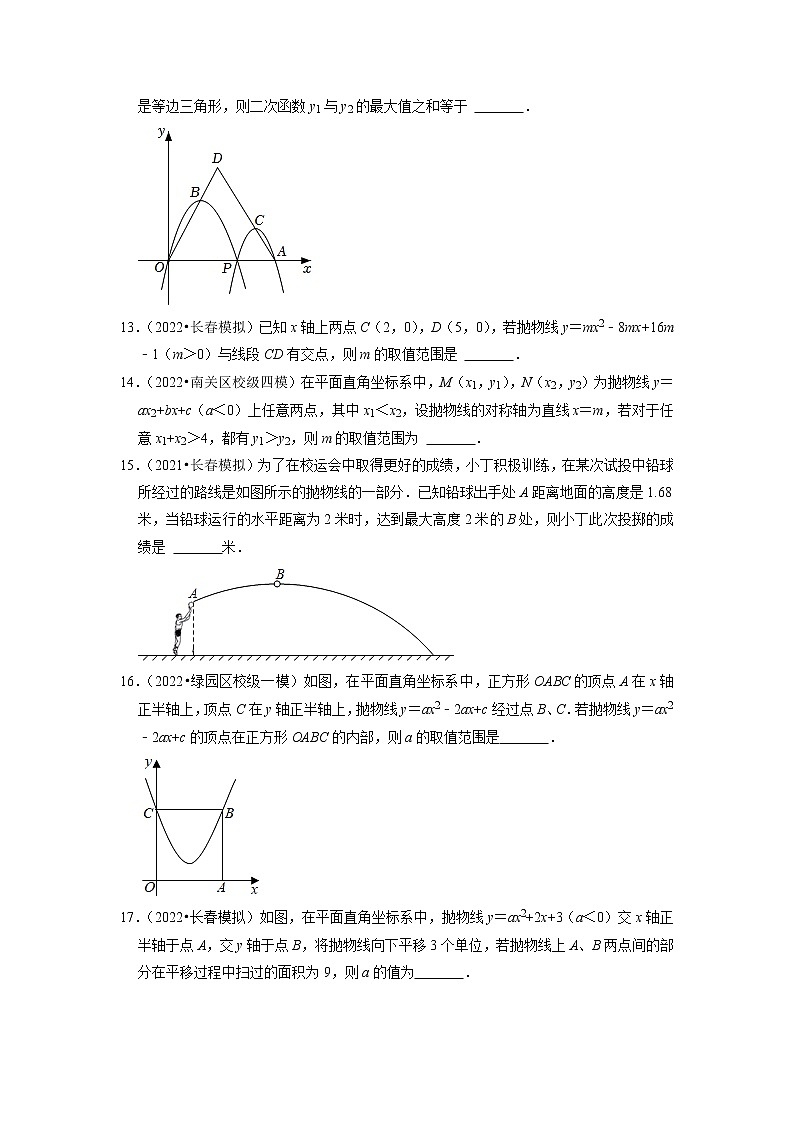
12.(2022•长春模拟)如图,在平面直角坐标系中,点A的坐标为(4,0),点P是线段OA上的一点(不与O、A重合),二次函数y1的图象经过O、P两点,y2的图象经过P、A两点,两条抛物线的开口均向下,顶点分别为B、C,射线OB与AC相交于点D.若△OAD是等边三角形,则二次函数y1与y2的最大值之和等于 .
13.(2022•长春模拟)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2﹣8mx+16m﹣1(m>0)与线段CD有交点,则m的取值范围是 .
14.(2022•南关区校级四模)在平面直角坐标系中,M(x1,y1),N(x2,y2)为抛物线y=ax2+bx+c(a<0)上任意两点,其中x1<x2,设抛物线的对称轴为直线x=m,若对于任意x1+x2>4,都有y1>y2,则m的取值范围为 .
15.(2021•长春模拟)为了在校运会中取得更好的成绩,小丁积极训练,在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是1.68米,当铅球运行的水平距离为2米时,达到最大高度2米的B处,则小丁此次投掷的成绩是 米.
16.(2022•绿园区校级一模)如图,在平面直角坐标系中,正方形OABC的顶点A在x轴正半轴上,顶点C在y轴正半轴上,抛物线y=ax2﹣2ax+c经过点B、C.若抛物线y=ax2﹣2ax+c的顶点在正方形OABC的内部,则a的取值范围是 .
17.(2022•长春模拟)如图,在平面直角坐标系中,抛物线y=ax2+2x+3(a<0)交x轴正半轴于点A,交y轴于点B,将抛物线向下平移3个单位,若抛物线上A、B两点间的部分在平移过程中扫过的面积为9,则a的值为 .
18.(2022•长春模拟)如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE=32.直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是 .
19.(2021•二道区校级一模)对于函数y=1ax2﹣2x+1(a≠0),当x≥1时,y随x的增大而增大,则a的取值范围是 .
20.(2021•吉林模拟)如图,在平面直角坐标系中,抛物线y=(x﹣h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为 .
三.解答题(共10小题)
21.(2021•长春)在平面直角坐标系中,抛物线y=2(x﹣m)2+2m(m为常数)的顶点为A.
(1)当m=12时,点A的坐标是 ,抛物线与y轴交点的坐标是 ;
(2)若点A在第一象限,且OA=5,求此抛物线所对应的二次函数的表达式,并写出函数值y随x的增大而减小时x的取值范围;
(3)当x≤2m时,若函数y=2(x﹣m)2+2m的最小值为3,求m的值;
(4)分别过点P(4,2)、Q(4,2﹣2m)作y轴的垂线,交抛物线的对称轴于点M、N.当抛物线y=2(x﹣m)2+2m与四边形PQNM的边有两个交点时,将这两个交点分别记为点B、点C,且点B的纵坐标大于点C的纵坐标.若点B到y轴的距离与点C到x轴的距离相等,直接写出m的值.
22.(2021•吉林)如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象经过点A(0,−74),点B(1,14).
(1)求此二次函数的解析式;
(2)当﹣2≤x≤2时,求二次函数y=x2+bx+c的最大值和最小值;
(3)点P为此函数图象上任意一点,其横坐标为m,过点P作PQ∥x轴,点Q的横坐标为﹣2m+1.已知点P与点Q不重合,且线段PQ的长度随m的增大而减小.
①求m的取值范围;
②当PQ≤7时,直接写出线段PQ与二次函数y=x2+bx+c(﹣2≤x<13)的图象交点个数及对应的m的取值范围.
23.(2022•南关区校级模拟)在平面直角坐标系中,函数y=ax2﹣2ax﹣4a(x≥0)的图象记为M1,函数y=﹣ax2﹣2ax+4a(x<0)的图象记为M2,其中a为常数,且a≠0.图象M1、M2,合起来得到的图象记为M.
(1)直接写出图象M2与x轴的交点坐标.
(2)当图象M1的最低点到x轴距离为2时,求a的值.
(3)当a=1时,若(m,−32)在图象M上,求m的值.
(4)点A、B、C、D的坐标分别为(﹣2,2)、(3,2)、(3,﹣1)、(﹣2,﹣1),当M1、M2的顶点均在矩形ABCD内部时,直接写出a的取值范围.
24.(2022•南关区校级一模)在平面直角坐标系中,抛物线y=x2﹣2mx+4m(x≤2m,m为常数)的图象记为G.
(1)当m=﹣2时,求图象G最低点的坐标.
(2)当图象G与x轴有且只有一个公共点时,求m的取值范围.
(3)当图象G的最低点到直线y=2的距离为3时,求m的值.
(4)图象G上点A的横坐标为2m,点C的坐标为(﹣2,3),当AC不与坐标轴平行时,以AC为对角线作矩形ABCD,使矩形的边与坐标轴平行,当图象G与矩形ABCD的边有两个公共点时,直接写出m的取值范围.
25.(2022•长春一模)已知抛物线y=x2﹣2mx+2m+1.
(1)写出抛物线y=x2﹣2mx+2m+1的顶点坐标(用含m的式子表示).
(2)当x≥1时,y随x的增大而增大,则m的取值范围是 .
(3)当﹣1≤x≤2时,函数y=x2﹣2mx+2m+1的图象记为G,设图象G的最低点的纵坐标为y0.当y0=﹣1时,求m的值.
(4)当m>0时,分别过点A(2,1)、B(2,4)作y轴垂线,垂足分别为点D、点C,抛物线在矩形ABCD内部的图象(包括边界)的最低点到直线y=﹣2的距离等于最高点到x轴的距离,直接写出m的值.
26.(2022•吉林模拟)如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象经过点A(0,﹣4),点B(4,0).
(1)求此二次函数的解析式.
(2)若点P是直线AB下方抛物线上一动点,当△PAB的面积最大时,求出点P的坐标和△PAB的最大面积.
(3)当t≤x≤t+3时,此二次函数的最大值为m,最小值为n,若m﹣n=3,直接写出t的值.
27.(2022•朝阳区校级一模)已知二次函数解析式为y=1ax2−a+2ax﹣1(a≠0),该抛物线与y轴交于点A,其顶点记为B,点A关于抛物线对称轴的对称点记为C.已知点D在抛物线上,且点D的横坐标为2,DE⊥y轴交抛物线于点E.
(1)求点D的纵坐标.
(2)当△ABC是等腰直角三角形时,求出a的值.
(3)当0≤x≤2时,函数的最大值与最小值的差为2时,求a的取值范围.
(4)设点R(a﹣3,﹣1),点A、R关于直线DE的对称点分别为N、M,当抛物线在以A、R、M、N为顶点的四边形内部的图象中,y随x的增大而增大或y随x的增大而减小时,直接写出a的取值范围.
28.(2022•南关区校级四模)在平面直角坐标系中,已知函数y=x2﹣2ax+2a(a为常数).
(1)若a=1.
①当0≤x≤3时,y的取值范围是 .
②若﹣2≤x≤b时,1≤y≤10,则b的取值范围是 .
(2)当0≤x≤12a+2时,此函数的最大值与最小值的差是4,求a的值.
(3)设此函数图象与y轴交点为点M,过点M作y轴的垂线l,将函数图象在直线l上方部分沿直线l翻折后的图象记为G1,原函数图象末翻折部分记为G2,G1与G2组成的图记为G,当G在直线x=32a+1与直线x=2a+12之间所夹的图象y随x增大而减小时,接写出a的取值范围.
29.(2022•长春模拟)在平面直角坐标系中,点A的坐标为(m,2)(其中m为常数),点B与点A关于y轴对称.在实数范围内定义函数y=x2+x−m(x≥1)x2+x+m(x<1)(其中m为常数)的图象为G.
(1)当点(﹣1,2)在G上时,求m的值;
(2)当点B在G上时,求m的值;
(3)m≠0时,连接AB,当G与线段AB恰好有两个公共点时,m= .
(4)当y最小值的取值范围是﹣2≤y最小值≤﹣1时,直接写出m的取值范围.
30.(2022•长春模拟)已知:在平面直角坐标系xOy中,点A(x1,y1)、B(x2,y2)是某函数图象上任意两点(x1<x2),将函数图象中x<x1的部分沿直线y=y1作轴对称,x>x2的部分沿直线y=y2作轴对称,与原函数图象中x1≤x≤x2的部分组成了一个新函数的图象,称这个新函数为原函数关于点A、B的“双对称函数”.
例如:如图①,点A(﹣2,﹣1)、B(1,2)是一次函数y=x+1图象上的两个点,则函数y=x+1关于点A、B的“双对称函数”的图象如图②所示.
(1)点A(t,y1)、B(t+3,y2)是函数y=3x图象上的两点,y=3x关于点A、B的“双对称函数”的图象记作G,若G是中心对称图形,直接写出t的值.
(2)点P(12,y1),Q(12+t,y2)是二次函数y=(x﹣t)2+2t图象上的两点,该二次函数关于点P、Q的“双对称函数”记作f.
①求P、Q两点的坐标(用含t的代数式表示).
②当t=﹣2时,求出函数f的解析式;
③若﹣1≤x≤1时,函数f的最小值为ymin,求﹣2≤ymin≤﹣1时,t的取值范围.
2022年吉林省中考数学专题练5-二次函数
参考答案与试题解析
一.选择题(共8小题)
1.【解答】解:∵y=2x2﹣4x+m,
∴抛物线开口向上,对称轴为直线x=−−42×2=1,
∴距离对称轴越近的点的纵坐标越小,
∵1﹣1<4﹣1<1﹣(﹣3),
∴y1<y2<y3.
故选:D.
2.【解答】解:根据题意得y=﹣2(x+2)2+1.
故选:D.
3.【解答】解:∵抛物线y=﹣x2+4x+m=﹣(x﹣2)2+4+m,
∴顶点A的坐标为(2,4+m),与y轴的交点D的坐标为(0,m),
∵BF∥CE,DE平行于x轴,
∴BC∥FE,
∴四边形BFEC是平行四边形,
∴BC=FE,
∴3S△ABC=4S△FEC,
∴3(4+m)=4•(﹣m),
解得m=−127,
故选:A.
4.【解答】解:∵抛物线对称轴为直线x=−2a−2a=1,
点B为(0,2),
∴点D坐标为(2,2),
BD=2﹣0=2.
∵CD=13BC,
∴CD=12BD=1,
∴BC=2+1=3.
∴S△ABC=12×3×2=3.
故选:D.
5.【解答】解:当k<1时,有﹣(1﹣k)2=﹣1,
解得:k1=0,k2=2(舍去);
当1≤k≤6时,y=﹣(x﹣k)2的最大值为0,不符合题意;
当k>6时,有﹣(6﹣k)2=﹣1,
解得:k3=5(舍去),k4=7.
综上所述:k的值为0或7.
故选:C.
6.【解答】解:∵函数y=(k﹣2)x2﹣2kx+k的图象与坐标轴共有三个交点,
∴k−2≠0k≠0(−2k)2−4(k−2)⋅k>0,
解得k>0且k≠2,
故选:C.
7.【解答】解:抛物线y=2x2﹣1向左平移1个单位长度,得:y=2(x+1)2﹣1;
再向上平移2个单位长度,得:y=2(x+1)2+1.
此时抛物线顶点坐标是(﹣1,1).
故选:D.
8.【解答】解:由题意可得,抛物线经过点(0,1.5)和(3,0),
把上述两个点坐标代入二次函数表达式得:
c=1.59a+3+c=0,
解得:a=−12c=32,
∴函数表达式为:y=−12x2+x+32,
=−12(x﹣1)2+2,
∵a<0,故函数有最大值,
∴当x=1时,y取得最大值,此时y=2,
答:水流喷出的最大高度为2米.
故选:C.
二.填空题(共12小题)
9.【解答】解:把A(2,4)代入y=ax2中得4=4a,
解得a=1,
∴y=x2,
设点C横坐标为m,则CD=CE=2m,
∴点E坐标为(m,4﹣2m),
∴m2=4﹣2m,
解得m=﹣1−5(舍)或m=﹣1+5.
∴CD=2m=﹣2+25.
故答案为:﹣2+25.
10.【解答】解:∵二次函数y=﹣x2+mx+3过点(4,3),
∴3=﹣16+4m+3,
∴m=4,
∴y=﹣x2+4x+3,
∵y=﹣x2+4x+3=﹣(x﹣2)2+7,
∴抛物线开口向下,对称轴是x=2,顶点为(2,7),函数有最大值7,
把y=3代入y=﹣x2+4x+3得3=﹣x2+4x+3,解得x=0或x=4,
∵当0≤x≤a时,y有最大值7,最小值3,
∴2≤a≤4.
故答案为:2≤a≤4.
11.【解答】解:∵y=(x﹣1)2+3,
∴该抛物线的顶点坐标为(1,3),且开口方向向上,
∴当x=1时,y取得最小值,
故答案为:1.
12.【解答】解:如图,连接PB、PC,
由二次函数的性质,OB=PB,PC=AC,
∵△ODA是等边三角形,
∴∠AOD=∠OAD=60°,
∴△POB和△ACP是等边三角形,
∵A(4,0),
∴OA=4,
∴点B、C的纵坐标之和为4×32=23,
即两个二次函数的最大值之和等于23.
故答案为23.
13.【解答】解:∵y=mx2﹣8mx+16m﹣1=m(x﹣4)2﹣1,m>0,
∴抛物线开口向上,顶点坐标为(4,﹣1),抛物线对称轴为直线x=4,
∵4﹣2>5﹣4,
∴m增大过程中,抛物线先经过点C,再经过点D,
将(2,0)代入y=mx2﹣8mx+16m﹣1得0=4m﹣1,
解得m=14,
∴m≥14时抛物线与CD有交点,
故答案为:m≥14.
14.【解答】解:∵y1>y2,
∴ax12+bx1+c>ax22+bx2+c,
∴a(x12﹣x22)>﹣b(x1﹣x2),
∵a<0,x1<x2,
∴x1﹣x2<0,
∴x1+x2>−ba=2m,
当x1+x2>4时,都有x1+x2>2m,
∴2m≤4,
∴m≤2,
∴满足条件的值为:m≤2.
故答案为:m≤2.
15.【解答】解:建立坐标系,如图所示:
由题意得:A(0,1.68),B(2,2),点B为抛物线的顶点,
设抛物线的解析式为y=a(x﹣2)2+2,
把A(0,1.68)代入得:
4a+2=1.68,
解得a=﹣0.08,
∴y=﹣0.08(x﹣2)2+2,
令y=0,得﹣0.08(x﹣2)2+2=0,
解得x1=7,x2=﹣3(舍),
∴小丁此次投掷的成绩是7米.
故答案为:7.
16.【解答】解:∵抛物线y=ax2﹣2ax+c开口向上,
∴a>0,
∵对称轴为直线x=−−2a2a=1,且经过点B、C.
∴BC=2,
∴正方形的边长为2,
∴C(0,2),B(2,2),
∴c=2,
∵抛物线为y=ax2﹣2ax+2,
∵抛物线y=ax2﹣2ax+c的顶点在正方形OABC的内部,
∴0<4a×2−(−2a)24a<2,
解得a<2,
∴0<a<2,
故答案为0<a<2.
17.【解答】解:如图,抛物线上A、B两点间的部分在平移过程中扫过的面积等于▱ABOC的面积,
∵平移过程中扫过的面积为9,
∴3•OA=9,
解得OA=3,
∴点A的坐标为(3,0),
代入得a•32+2×3+3=0,
解得a=﹣1.
故答案为:﹣1.
18.【解答】解:由tan∠AOE=32,可设A、B点坐标分别为(2m,3m)、(2n,3n),
∵AD∥OC,
∴∠ADB=∠OCB,∠DAB=∠COA,
∴△BAD∽△BOC.
①当点A在线段OB上时,如图1所示.
∵OC=2AD,
∴D点为线段BC的中点,
∵C(0,c),B(2n,3n),
∴D点横坐标为0+2n2=n,
由题意知A、D点均在抛物线的对称轴上,
∴n=2m,
∴B点坐标为(4m,6m),
∵A,B在抛物线上,且抛物线对称轴为x=2m,
∴有3m=4m2+2bm+c6m=16m2+4bm+c−b2=2m,
解得:m=0b=0c=0,或m=34b=−3c=92,
∵c>0,
∴c=92;
②当点B在线段OA上时,如图2所示.
∵OC=2AD,
∴OB=2AB.
∵C(0,c),B(2n,3n),
∴D点横坐标为1+22×2n=3n,
由题意知A、D点均在抛物线的对称轴上,
∴n=23m,
∴B点坐标为(43m,2m),
∵A,B在抛物线上,且抛物线对称轴为x=2m,
∴有3m=4m2+2bm+c2m=169m2+43bm+c−b2=2m,
解得:m=0b=0c=0,或m=−94b=9c=272.
∵c>0,
∴c=272.
综上所述:c的值为92或272.
故答案为:92或272.
19.【解答】解:∵当x≥1时,y随x的增大而增大,
∴抛物线开口向上,a>0,
∵抛物线对称轴为直线x=−−22a=a,
∴a≤1,
∴0<a≤1,
故答案为:0<a≤1.
20.【解答】解:∵y=(x﹣h)2与x轴只有一个交点M,
∴M(h,0),对称轴为x=h,
∵抛物线与平行于x轴的直线l交于A,B两点,
∴A,B两点的纵坐标相同,设为a,
则a=(x﹣h)2时,x﹣h=±a,
解得:x=h±a,
∴点A的横坐标是(h−a),点B的横坐标是(h+a),
∵AB=3,
∴(h+a)﹣(h−a)=3,
解得:a=94;
故答案为:94.
三.解答题(共10小题)
21.【解答】解:(1)当m=12时,y=2(x−12)2+1,
∴顶点A(12,1),
令x=0,得y=32,
∴抛物线与y轴交点的坐标为(0,32),
故答案为:(12,1),(0,32);
(2)∵点A(m,2m)在第一象限,且OA=5,
∴m2+(2m)2=(5)2,且m>0,
解得:m=1,
∴抛物线的解析式为y=2(x﹣1)2+2,当x≤1时,函数值y随x的增大而减小;
(3)∵当x≤2m时,若函数y=2(x﹣m)2+2m的最小值为3,
∴分两种情况:2m<m,即m<0时,或2m>m,即m>0时,
①当m<0时,2(2m﹣m)2+2m=3,
解得:m=−1+72(舍)或m=−1+72,
②当m>0时,2(m﹣m)2+2m=3,
解得:m=32,
综上所述,m的值为32或−1+72;
(4)P(4,2)、Q(4,2﹣2m),抛物线y=2(x﹣m)2+2m,
①当m>1时,如图1,
∵2m>2,2﹣2m<0,
∴抛物线y=2(x﹣m)2+2m与四边形PQNM的边没有交点;
②当m=1时,如图2,
∵2m=2,2﹣2m=0,
∴抛物线y=2(x﹣m)2+2m的顶点在边PM边上,
即抛物线y=2(x﹣m)2+2m与四边形PQNM的边只有一个交点;
③当12≤m<1时,如图3,
∵1≤2m<2,0<2﹣2m≤1,P(4,2)、Q(4,2﹣2m),
∴M(m,2),N(m,2﹣2m),
抛物线y=2(x﹣m)2+2m与四边形PQNM的边有两个交点,若点B在PM边上,点C在MN边上,
∴令y=2,则2=2(x﹣m)2+2m,
∴x=m+1−m 或 x=m−1−m(不合题意,应舍去),
∴B(m+1−m,2),C(m,2m),
根据题意,得2m=m+1−m,
解得:m=5−12或m=−5−12(不合题意,应舍去);
④当0≤m<12时,如图4,
∴点B在PM边上,点C在NQ边上,
∴B(m+1−m,2),C(m+1−2m,2﹣2m),
则2﹣2m=m+1−m,
解得:m=11±1318,
∵0≤m<12,
∴m=11−1318,
⑤当m<0时,如图5,
∵2m<0,2﹣2m>2,
∴点B在NQ边上,点C在PM边上,
B(m+1−2m,2﹣2m),C(m+1−m,2)
则|m+1−2m|=2,
当m+1−2m=2时,得m2﹣2m+3=0,
∵Δ=(﹣2)2﹣4×1×3=﹣8<0,
∴该方程无解;
当m+1−2m=−2时,得m2+6m+3=0,
解得:m=﹣3−6或m=﹣3+6,
当m=﹣3+6时,
|m+1−2m|=|﹣3+6+1−2(−3+6)|=26−4≠2,
不符合题意,舍去,
综上所述,m的值为5−12或11−1318或﹣3−6.
22.【解答】解:(1)将A(0,−74),点B(1,14)代入y=x2+bx+c得:
−74=c14=1+b+c,
解得b=1c=−74,
∴y=x2+x−74.
(2)∵y=x2+x−74=(x+12)2﹣2,
∵抛物线开口向上,对称轴为直线x=−12.
∴当x=−12时,y取最小值为﹣2,
∵2﹣(−12)>−12−(﹣2),
∴当x=2时,y取最大值22+2−74=174.
(3)①PQ=|﹣2m+1﹣m|=|﹣3m+1|,
当﹣3m+1>0时,PQ=﹣3m+1,PQ的长度随m的增大而减小,
当﹣3m+1<0时,PQ=3m﹣1,PQ的长度随m增大而增大,
∴﹣3m+1>0满足题意,
解得m<13.
②∵0<PQ≤7,
∴0<﹣3m+1≤7,
解得﹣2≤m<13,
如图,当m=−12时,点P在最低点,PQ与图象有1交点,
m增大过程中,−12<m<13,点P与点Q在对称轴右侧,PQ与图象只有1个交点,
直线x=13关于抛物线对称轴直线x=−12对称后直线为x=−43,
∴−43<m<−12时,PQ与图象有2个交点,
当﹣2≤m≤−43时,PQ与图象有1个交点,
综上所述,﹣2≤m≤−43或−12≤m<13时,PQ与图象交点个数为1,−43<m<−12时,PQ与图象有2个交点.
23.【解答】解:(1)对y=﹣ax2﹣2ax+4a,令y=0,则﹣ax2﹣2ax+4a=0,
∴﹣x2﹣2x+4=0,
解得x=5−1或x=−5−1,
∴图象M2与x轴的交点坐标为(5−1,0)或(−5−1,0);
(2)∵y=ax2﹣2ax﹣4a=a(x﹣1)2﹣5a,
∴抛物线的对称轴为直线x=1,
∵x≥0,
当a>0时,函数的最低点的纵坐标为﹣5a,
∴|﹣5a|=2,
∴a=25;
当a<0时,函数无最小值,
∴此情况不满足;
综上所述:a=25;
(3)当a=1时,y=x2﹣2x﹣4(x≥0),y=﹣x2﹣2x+4(x<0),
当m≥0时,−32=m2﹣2m﹣4,解得m=172+1;
当m<0时,−32=−x2﹣2x+4,解得m=−262−1;
综上所述:m的值为172+1或−262−1;
(4)∵y=ax2﹣2ax﹣4a=a(x﹣1)2﹣5a,
∴图象M1的顶点(1,﹣5a),
∵y=﹣ax2﹣2ax+4a=﹣a(x+1)2+5a,
∴图象M2的顶点为(﹣1,5a),
如图1,当a>0时,﹣5a≥﹣1,5a≤2,
∴0<a≤15;
如图2,当a<0时,﹣5a≤2,5a≥﹣1,
∴−15≤a<0;
综上所述:a的取值范围为−15≤a≤15且a≠0.
24.【解答】解:(1)当m=﹣2时,y=x2+4x﹣8,
∴y=x2+4x﹣8=(x+2)2﹣12,
∵x≤﹣4,
∴当x=﹣4时,y=﹣8,
∴图象G最低点的坐标(﹣4,﹣8);
(2)∵y=x2﹣2mx+4m=(x﹣m)2﹣m2+4m,
∴抛物线的对称轴为直线x=m,
令y=0,则x2﹣2mx+4m=0,
∴Δ=4m2﹣16m=0,
∴m=0或m=4,
当m≤0时,2m≤m,
∴图象G与x轴始终有一个公共点,
当m=4时,图象G与x轴只有一个公共点,
当m>4时,2m>m,图象G与x轴始终有两个公共点;
当0<m<4时,Δ<0,此时图象G与x轴无公共点;
综上所述:m≤0或m=4时,图象G与x轴只有一个公共点;
(3)∵图象G的最低点到直线y=2的距离为3,
∴图象G的最低点的纵坐标为﹣1或5,
当m<0时,m>2m,
此时当x=2m时,y=4m,
此时最低点的纵坐标为4m,
∴4m=﹣1,
∴m=−14;
当m>0时,2m>m,
∴当x=m时,y=4m﹣m2,
此时最低点的纵坐标为4m﹣m2,
∴4m﹣m2=﹣1或4m﹣m2=5,
解得m=2+5或m=2−5(舍);
综上所述:m的值为−14或2+5;
(4)∵点A在图象G上,
∴图象G与矩形ABCD一定有一个公共点,
∵图象G与矩形ABCD的边有两个公共点,
∴只需图象G与矩形ABCD的边再由一个公共点即可;
∵点A的横坐标为2m,
∴A(2m,4m),
当x=﹣2时,y=4+8m,
当4+8m=4m时,m=﹣1,
如图1,当m<﹣1时,图象G在x≤2m时,y随x的增大而减小,
∴矩形与图象G只有一个交点A;
当﹣1<m≤0时,图象G与矩形有两个交点;
当4m=3时,m=34,
如图3,当0<m<34时,2m>m,
∴图象G与矩形ABCD有三个交点;
当y=3时,x2﹣2mx+4m=3,
整理得,x2﹣2mx+4m﹣3=0,
∴Δ=4m2﹣16m+12=0,
∴m=1或m=3,此时图象G与BC边有一个交点,
如图4,当34<m≤1时,图象G与矩形有三个交点;
如图5,当1<m<3时,图象G与矩形有两个交点;
当m=3时,图象G与矩形有三个交点;
当m>3时,图象G与矩形有四个交点;
综上所述:﹣1<m≤0或1<m<3时,图象G与矩形ABCD有两个交点.
25.【解答】解:(1)∵y=x2﹣2mx+2m+1=(x﹣m)2﹣m2+2m+1,
∴顶点坐标为(m,﹣m2+2m+1);
(2)∵抛物线开口向上,
∴m≤1时,y随x的增大而增大,
故答案为:m≤1;
(3)当m<﹣1时,x=﹣1,函数有最小值,
∴y0=2+4m,
∵y0=﹣1,
∴2+4m=﹣1,
解得m=−34(舍);
当m>2时,x=2,函数有最小值,
∴y0=5﹣2m,
∵y0=﹣1,
∴5﹣2m=﹣1,
解得m=3;
当﹣1≤m≤2时,x=m,函数有最小值,
∴y0=﹣m2+2m+1,
∵y0=﹣1,
∴﹣m2+2m+1=﹣1,
解得m=3+1(舍)或m=−3+1;
综上所述:m的值为3或−3+1;
(4)当0<m≤12时,﹣m2+2m+1+2=4,
解得m=1(舍);
当12<m≤1时,﹣m2+2m+1+2=4﹣2m+1,
解得m=6+2(舍)或m=−6+2(舍);
当1<m≤32时,﹣m2+2m+1+2=2m+1,
解得m=2或m=−2(舍);
当32<m≤2时,﹣m2+2m+1+2=4,
解得m=1(舍);
当m>2时,最高点纵坐标是4,最低点纵坐标是1,
∴3≠4,
∴此时不符合题意;
综上所述:m的值为2.
26.【解答】解:(1)将点A(0,﹣4),点B(4,0)代入y=x2+bx+c,
∴c=−416+4b+c=0,
∴c=−4b=−3,
∴y=x2﹣3x﹣4;
(2)过点P作PQ∥y轴交AB于点Q,
设直线AB的解析式为y=kx+b,
∴b=−44k+b=0,
解得k=1b=−4,
∴y=x﹣4,
设P(t,t2﹣3t﹣4),则Q(t,t﹣4),
∴PQ=t﹣4﹣(t2﹣3t﹣4)=﹣t2+4t,
∴S△PAB=12×4×(﹣t2+4t)=﹣2t2+8t=﹣2(t﹣2)2+8,
∵0<t<4,
∴t=2时,△PAB的面积最大值为8,
此时P(2,﹣6);
(3)∵y=x2﹣3x﹣4=(x−32)2−254,
∴抛物线的对称轴为直线x=32,
当x=t时,y=t2﹣3t﹣4,
当x=t+1时,y=(t+1)2﹣3(t+1)﹣4=t2﹣t﹣6,
①当t+1<32,即t<12时,m=t2﹣3t﹣4,n=t2﹣t﹣6,
∴m﹣n=t2﹣3t﹣4﹣(t2﹣t﹣6)=﹣2t+2=3,
解得t=−12;
②当t>32时,m=t2﹣t﹣6,n=t2﹣3t﹣4,
∴m﹣n=2t﹣2=3,
解得t=52;
③当t≤32≤t2+1,即1≤t≤32时,m=t2﹣t﹣6,n=−254,
∴m﹣n=t2﹣t﹣6+254=3,
解得t=3+12(舍)或t=−3+12(舍);
④t2+1≤32≤t+1,即12≤t≤1时,m=t2﹣3t﹣4,n=−254,
∴m﹣n=t2﹣3t﹣4+254=3,
解得t=3+32(舍)或t=−3+32(舍);
综上所述:t的值为52或−12.
27.【解答】解:(1)当x=2时,y=﹣3,
∴D(2,﹣3);
(2)令x=0,则y=﹣1,
∴A(0,﹣1),
∵y=1ax2−a+2ax﹣1=1a(x−a+22)2−a2+8a+44a,
∴顶点B(a+22,−a2+8a+44a),
∵抛物线的对称轴为直线x=a+2a,
∴C(a+2,﹣1),
∵△ABC是等腰直角三角形,
∴AB⊥BC,
∴|a+22|=|﹣1+a2+8a+44a|,
解得a=±2或a=−23,
当a=﹣2时,B(0,1),C(0,﹣1),此时C点与A点重合,
∴a=﹣2(舍);
∴a=﹣2或a=−23;
(3)∵抛物线的对称轴为直线x=a+2a,
①当a+22<0时,a<﹣2,
此时当x=0时,函数有最大值﹣1,
当x=2时,函数有最小值﹣3,
∴函数的最大值与最小值的差为2;
②当a+22>2时,a>2,
此时当x=0时,函数有最大值﹣1,
当x=2时,函数有最小值﹣3,
∴函数的最大值与最小值的差为2;
③当0≤a+22≤1时,﹣2≤a<0,
此时当x=a+22,函数有最大值−a2+8a+44a,
当x=2时,函数有最小值﹣3,
∵函数的最大值与最小值的差为2,
∴−a2+8a+44a+3=2,
∴a2+8a+44a=1,
解得a=﹣2;
④当1<a+22≤2时,0<a≤2,
此时当x=0时,函数有最大值﹣1,
当x=a+22时,函数有最小值−a2+8a+44a,
∵函数的最大值与最小值的差为2,
∴﹣1+a2+8a+44a=2,
∴a2+8a+44a=3,
解得a=2;
综上所述:a≤﹣2或a≥2时,函数的最大值与最小值的差为2;
(4)∵D(2,﹣3),DE⊥y轴,
∴DE所在直线为y=﹣3,
∵A(0,﹣1),R(a﹣3,﹣1),
∴N(0,﹣5),R(a﹣3,﹣5),
当a>0时,1a(a﹣3)2−a+2a•(a﹣3)﹣1≤﹣5,
解得a≥15,
此时抛物线在以A、R、M、N为顶点的四边形内部的图象,y随x的增大而减小;
当a<0时,−a2+8a+44a≥−1,
解得a<0,
此时此时抛物线在以A、R、M、N为顶点的四边形内部的图象,y随x的增大而增大;
综上所述:a≥15或a<0时,符合题意.
28.【解答】解:(1)当a=1时,y=x2﹣2x+2=(x﹣1)2+1,
∴顶点坐标为(1,1),
①当0≤x≤3时,当x=0,y=2,当x=3,y=5,
∴y的取值范围是1≤y≤5,
故答案为:1≤y≤5;
②当1≤y≤10时,当y=1,x=1,当y=10,x=﹣2或4,
∵﹣2≤x≤b,
∴1≤b≤4,
故答案为:1≤b≤4;
(2)∵0≤12a+2,
∴a≥﹣4,
∵y=x2﹣2ax+2a=(x﹣a)2+2a﹣a2,
∴顶点坐标为(a,2a﹣a2),
当﹣4≤a≤0时,最低点(0,2a),最高点为(12a+2,−34a2+4),
∴−34a2+4﹣2a=4,
∴a=0或−83,
当0<a≤43时,最低点(a,2a﹣a2),最高点为(12a+2,−34a2+4),
∴−34a2+4﹣(2a﹣a2)=4,
∴a=0(舍去)或8(舍去),
当43<a≤4时,最低点(a,2a﹣a2),最高点为(0,2a),
∴2a﹣(2a﹣a2)=4,
∴a=2或﹣2(舍去),
当a>4时,不合题意,
综上所述:a=0或−83或2;
(3)当32a+1>2a+12时,即a<1,
当对称轴在y轴左侧时,即a<0,
由题意可得:2a+12≥2a32a+1≤a或2a+12≥0,
解得:a≤﹣2或−14≤a<0,
当对称轴在y轴右侧或y轴上时,a≥0,
由题意可得:32a+1≤a2a+12≥0或2a+12≥2a,
解得:a≤−14(舍去)或0≤a<1,
即a≤﹣2或−14≤a<1,
当32a+1<2a+12时,即a>1,
由题意可得:32a+1≥02a+12≤a或32a+1≥2a,
解得:−23≤a≤−12(舍去)或1<a≤2,
综上所述:a≤﹣2或−14≤a<1或1<a≤2.
29.【解答】解:(1)把点(﹣1,2)代入y=x2+x+m,则1﹣1+m=2,
∴m=2;
(2)∵点A的坐标为(m,2)(其中m为常数),点B与点A关于y轴对称,
∴点B的坐标为(﹣m,2),
当﹣m≥1时,即m≤﹣1时,
把点(﹣m,2)代入y=x2+x﹣m,则m2﹣m﹣m=2,解得m=1±3,(舍去)
当﹣m<1时,即m>﹣1时,
把点(﹣m,2)代入y=x2+x+m,则m2﹣m+m=2,解得m=±2,(负值舍去),
综上,m=2;
(3)当m<0时不存在两个交点,
当m>0时存在两个交点,此时只有一种情况成立,
即y=x2+x+m=2时,且△=1﹣4(m﹣2)=0,
解得m=94符合题意,
故答案为:94;
(4)当图形G上最低点落在函数y=x2+x﹣m(x≥1)的图象上时,则最低点坐标为(1,2﹣m),
∴﹣2≤2﹣m≤﹣1,
解得:3≤m≤4;
当图形G上最低点落在函数y=x2+x﹣m(x<2)的图象上时,
同理:−74≤m≤−34;
y=x2+x+m的顶点C(−12,m−14),
当x=1时,y=x2+x﹣m的点D(1,2﹣m),
m−14=2﹣m,
解得m=98,
当m>98时,D为最低点;
当m<98时,C为最低点.
综上所述,m的取值范围为:3≤m≤4或−74≤m≤−34.
30.【解答】解:(1)如图1,设点A(t,3t),B(t+3,3t+3),
∵G是中心对称图形,由反比例函数图象的中心对称性质可知:A与B关于原点成中心对称,
∴t+t+3=0,解得:t=−32;
(2)①y1=(12−t)2+2t=t2+t+14,y2=(12+t−t)2+2t=2t+14,
∴P(12,t2+t+14),Q(12+t,2t+14),
②如图2,当t=﹣2时,y=(x+2)2﹣4,P(12,94),Q(−32,−154),
根据“双对称函数”定义可知:
新图象f:由x<−32时抛物线y=(x+2)2﹣4沿直线y=−154翻折所得图象、x>12时抛物线y=(x+2)2﹣4沿直线y=94翻折所得图象及−32≤x≤12时抛物线y=(x+2)2﹣4三个部分组成,
∴当t=﹣2时,函数f的解析式为:y=y=−(x+2)2−72(x<−32),y=(x+2)2−4(−32≤x≤12),y=−(x+2)2+172(x>12);
③∵当﹣1≤x≤1时,函数f的最小值为ymin,且﹣2≤ymin≤﹣1,
若t<0,该二次函数关于点P、Q的“双对称函数”为:y=−(x−t)2+2t+12(x<12+t),(x−t)2+2t(12+t≤x≤12)−(x−t)2+2t2+12(t>12),
当t≤−12时,x=﹣1时,y=﹣1,则有(﹣1﹣t)2+2t=﹣1,
解得t=﹣2−2或﹣2+2(舍弃),
当x=﹣1,y=﹣2时,则有(﹣1﹣t)2+2t=﹣2,
解得t=﹣3或﹣1(舍弃),
由题意,满足条件的t的值为:﹣2−2≤t≤﹣3,
当−12≤t<0时,
当点Q是最低点时,x=t+12时,y=﹣2,可得t=−98,
当x=1时,y=﹣1,则有﹣(1﹣t)2+2t2+12=−1,
解得t=−2+22或−2−22(舍弃)
由题意,满足条件的t的值为:−98≤t≤−2+22,
当t≥0时,由﹣2≤﹣(﹣1﹣t)2+2t2+12≤−1,
可解得:2−22≤t≤2+22,
综上所述,t的取值范围为:﹣2−2≤t≤﹣3或−98≤t≤−2+22或2−22≤t≤2+22.
相关试卷
这是一份中考数学专题练——5二次函数,共26页。试卷主要包含了的图象上,+2的最小值为 等内容,欢迎下载使用。
这是一份中考数学专题练——专题8 二次函数及其应用(试题精选,含答案),共40页。
这是一份2023年徐州市中考数学专题练——5二次函数,文件包含5二次函数答案解析pdf、2023年徐州市中考数学专题练5二次函数pdf等2份试卷配套教学资源,其中试卷共49页, 欢迎下载使用。








