2020年初升高数学衔接课程 第15讲 指数函数（教师版含解析）练习题

这是一份2020年初升高数学衔接课程 第15讲 指数函数（教师版含解析）练习题，共13页。试卷主要包含了指数函数的图像及性质等内容，欢迎下载使用。
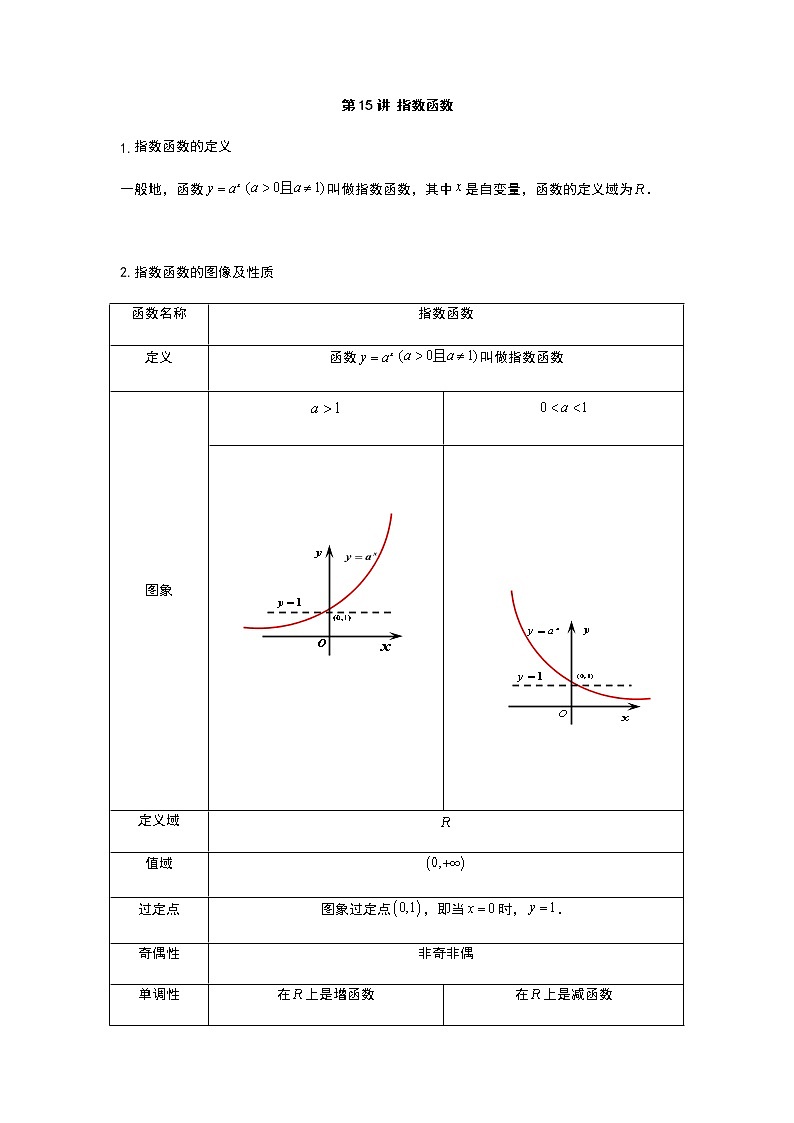
第15讲 指数函数指数函数的定义一般地，函数叫做指数函数，其中是自变量，函数的定义域为. 2.指数函数的图像及性质函数名称指数函数定义函数叫做指数函数图象          定义域值域过定点图象过定点，即当时，．奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化情况变化对 图象的影响在第一象限内，越大图象越高；在第二象限内，越大图象越低．   例1.在下列的关系式中，哪些不是指数函数，为什么？(1)  (2)  (3)  (4)      (5)   (6)   (7) (8)(，且)【答案】(1)(2)(3)(5)(6)(7)不是 例2.比较下列各题中两个值的大小：(1)       (2)   (3)       (4) 【答案】(1)；(2)；(3)；(4)    例3.函数的图象一定通过点          .【答案】 例4.若函数的图像经过第一、三、四象限，则一定有(    )A.      B.C.      D.【答案】A【解析】依题意该函数为增函数且在轴截距为负，所以，解得，选A.    例5. 二次函数与指数函数的图象只可能是  (    ) A     B    C    D【答案】A【解析】由指数函数可知同号且不相等，则二次函数的对称轴可排除B与D，C错误：易知，所以，此时单调递增，A正确：易知，所以，此时单调递减. 例6.解方程：  .【答案】【解析】由得，所以，解得. 例7.求下列不等式的解集：（1） ；      (2) 【答案】(1)；(2)时解集为，时解集为【解析】(1)由得，所以，解得，故解集为；(2)当时，由得，解得；当时，由得，解得或，综上所述，时解集为，时解集为.例8.求函数的定义域和值域：（1）；      (2)  ；           （3）；      (4)【答案】(1)定义域为，值域为；(2)定义域为，值域为；(3)定义域为，值域为；(4)定义域为，值域为.【解析】(1)定义域为，且为减函数，，值域为；（2）由得，，解得，定义域为，由可知，值域为；（3）定义域为，且为减函数，，值域为；（4）由解得，定义域为，由可知，且，则，值域为. 例9.(1)求函数的单调区间；       (2)求函数的单调减区间.【答案】(1)单调增区间为，单调减区间为；(2)单调减区间为.【解析】(1)定义域为，是由，复合而成的，为增函数，在上为增函数，在上为减函数，由复合函数单调性的同增异减性可知：的单调增区间为，单调减区间为；(2)定义域为，是由和复合而成的，为减函数，在上为减函数，在上为增函数，的单调减区间为. 例10.           方程的实数解的个数为        .【答案】2【解析】由得，画出函数的图象，由图可知函数的图象有两个交点，故方程的实数解的个数为2. 跟踪训练    下列函数中，可以称为指数函数的是(   )A.   B.   C.    D.【答案】A     下列关系式中正确的是 (    )A.     B.C.     D. 【答案】C     设满足，下列不等式中正确的是(    )A.    B.    C.    D. 【答案】C【解析】A错误：由指数函数在上为减函数且可知；B错误：由指数函数在上为减函数且可知；C正确：由幂函数在上为增函数且可知；D错误：由幂函数在上为增函数且可知，故选C.     函数的图象如图，其中为常数，则下列结论正确的是(   )A．  B．C．  D．【答案】D【解析】由图知为减函数，，又，，即，选D.     指数函数①，②，③，④的图象如图,则与1的大小关系是(      )A.      B.    C.      D.【答案】B【解析】 作直线与四个图形分别交于四点，则，由图可知，故选B.     函数图象的大致形状是  (      )   A      B       C     D【答案】D【解析】易知且，选D.     已知指数函数图像经过点，则__________.【答案】【解析】设该指数函数为，将点代入得，解得，，.     函数的图象恒过定点____________.【答案】      如果指数函数在上是减函数，那么实数的取值范围是_________.【答案】【解析】在上是减函数，，解得，所以的取值范围是.  若函数的图象经过第二、三、四象限，则的取值范围分别是_____________.【答案】，【解析】依题意该函数为减函数且在轴截距为负，所以，解得，所以的取值范围分别是，.  方程的实根的个数为___________.【答案】2【解析】由得，作出和的图象，由图可知两个函数图象有2个交点，故方程由2个实根.  解方程：(1) ；    (2)【答案】(1)；(2)【解析】(1)，，，，，；(2)，，，，，. 解不等式：(1) ；    (2)【答案】(1)；(2)时，时.【解析】(1)，解得；(2)若，则，解得；若，则，解得.  求函数的值域.【答案】【解析】当时，，是减函数，值域为，即.  讨论函数的单调性.【答案】单调增区间为，减区间为.【解析】定义域为，是由和复合而成的，为减函数，在，即上为减函数，在，即上为增函数，的单调增区间为，减区间为.        已知函数.(1)    判断的单调性和奇偶性；(2)    当时，解不等式.【答案】(1)在上单调递增，为奇函数；(2).【解析】(1)定义域为，任取且，则，当时，，，则，即；当时，，，则，即，综上所述，对任意的，均有，故在上单调递增，，为奇函数；(2)由是奇函数知等价于，由在上单调递增，所以，解得.