


专题17 规律探究类的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1
展开最长边长为128的整数边三角形有多少个?(整数边三角形是指三边长度都是整数的三角形.)
问题探究:
为了探究规律,我们先从最简单的情形入手,从中找到解决问题的方法,最后得出一般性的结论.
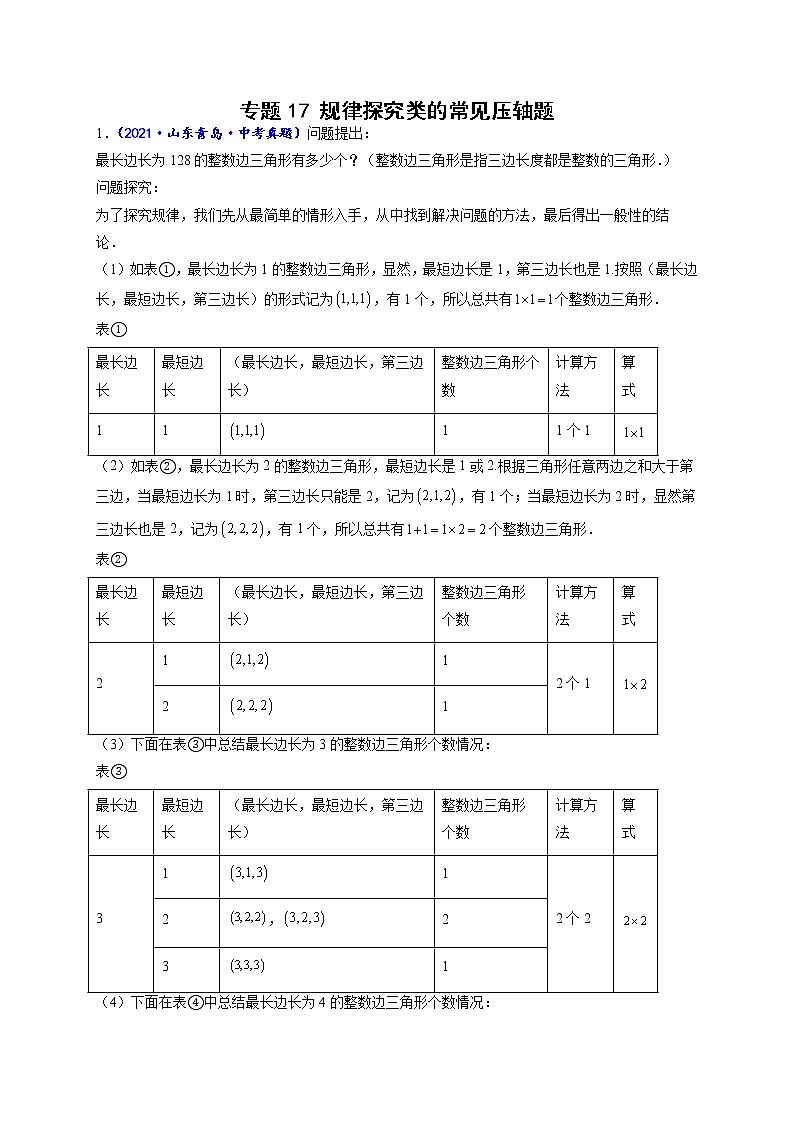
(1)如表①,最长边长为1的整数边三角形,显然,最短边长是1,第三边长也是1.按照(最长边长,最短边长,第三边长)的形式记为,有1个,所以总共有个整数边三角形.
表①
(2)如表②,最长边长为2的整数边三角形,最短边长是1或2.根据三角形任意两边之和大于第三边,当最短边长为1时,第三边长只能是2,记为,有1个;当最短边长为2时,显然第三边长也是2,记为,有1个,所以总共有个整数边三角形.
表②
(3)下面在表③中总结最长边长为3的整数边三角形个数情况:
表③
(4)下面在表④中总结最长边长为4的整数边三角形个数情况:
表④
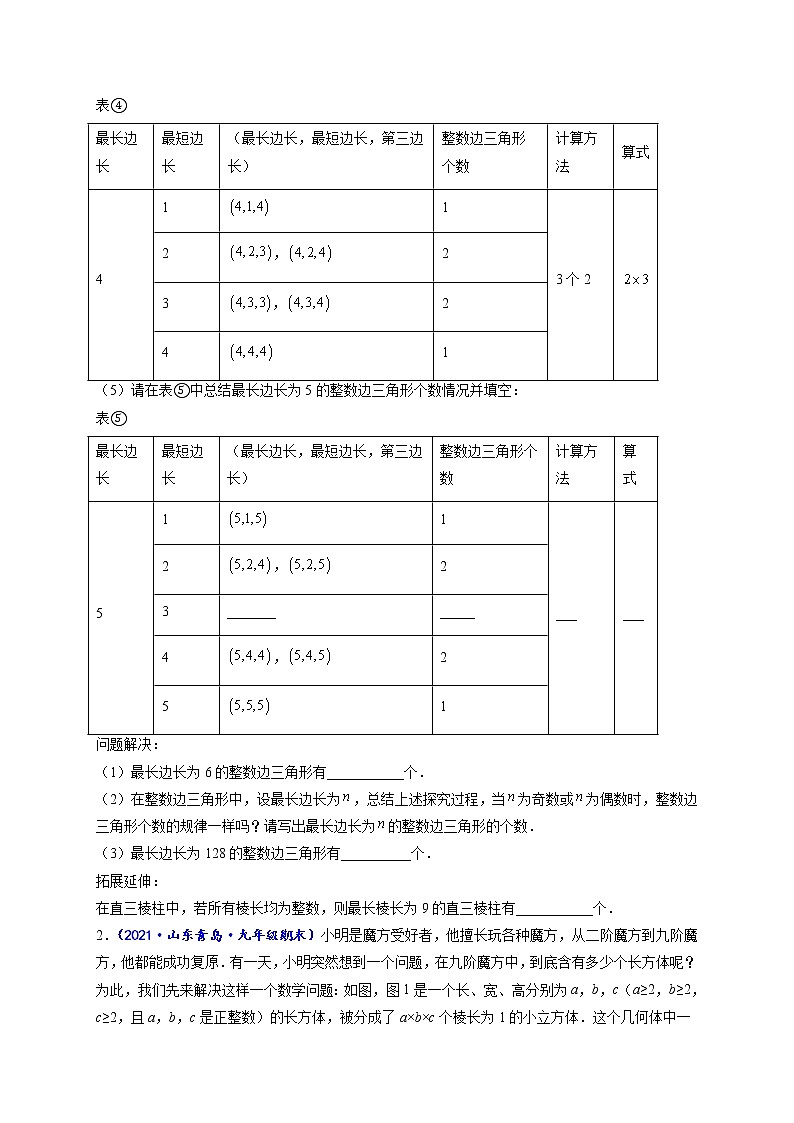
(5)请在表⑤中总结最长边长为5的整数边三角形个数情况并填空:
表⑤
问题解决:
(1)最长边长为6的整数边三角形有___________个.
(2)在整数边三角形中,设最长边长为,总结上述探究过程,当为奇数或为偶数时,整数边三角形个数的规律一样吗?请写出最长边长为的整数边三角形的个数.
(3)最长边长为128的整数边三角形有__________个.
拓展延伸:
在直三棱柱中,若所有棱长均为整数,则最长棱长为9的直三棱柱有___________个.
2.(2021·山东青岛·九年级期末)小明是魔方受好者,他擅长玩各种魔方,从二阶魔方到九阶魔方,他都能成功复原.有一天,小明突然想到一个问题,在九阶魔方中,到底含有多少个长方体呢?为此,我们先来解决这样一个数学问题:如图,图1是一个长、宽、高分别为a,b,c(a≥2,b≥2,c≥2,且a,b,c是正整数)的长方体,被分成了a×b×c个棱长为1的小立方体.这个几何体中一共包含多少个长方体(包括正方体)?(参考公式:1+2+3…+n).
问题探究:为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论.
探究一:如图2,该几何体有1个小立方体组成,显然,该几何体共有1个长方体.如图3,该几何体有2个小立方体组成,那么它一共包含1+2=3个长方体.如图4,该几何体有3个小立方体组成,那么它一共包含 个长方体.如图5,该几何体﹣共包含210个长方体,那么该几何体共有 个小立方体组成.
探究二:如图6,该几何体有4个小立方休组成,那么它一共包含(1+2)×(1+2)=9个长方体.如图7,该几何体有6个小立方体组成,那么它一共包含 个长方体.如图8,该几何体共有2m个小立方体组成,那么该几何体一共有 个长方体.
探究三:如图1,该几何体共有个a×b×c小立方体组成,那么该几何体共有 个长方体.
探究四:我们现在可以解决小明开始的问题了.在九阶魔方(即a=b=c=9)中,含有 个长方体.
探究五:聪明的小明在学习了三种视图后,又提出一个新的问题:在图1中,若a=6,b=4,c=5,如果拿走一些小立方体后,剩下几何体的三种枧图与原图1的三种视图完全一样,那么最多可以拿走 个小立方体;此时,剩下的几何体的表面积是 .
3.(2021·沙坪坝·重庆八中九年级开学考试)根据阅读材料,解决问题.
材料1:若一个正整数,从左到右各位数上的数字与从右到左各位数上的数字对应相同,则称为“对称数”(例如:1、232、4554是对称数).
材料2:对于一个三位自然数,将它各个数位上的数字分别2倍后取个位数字,得到三个新的数字,,,我们对自然数规定一个运算:(A),
例如:是一个三位的“对称数”,其各个数位上的数字分别2倍后取个位数字分别是:2、8、2.则.
请解答:
(1)请你直接写出最大的两位对称数: ,最小的三位对称数: ;
(2)如果将所有对称数按照从小到大的顺序排列,请直接写出第1100个对称数 ;
(3)一个四位的“对称数” ,若(B),请求出的所有值.
4.(2021·青岛大学附属中学九年级开学考试)(实际问题)小明家住楼.一天,他要把一根米长的竹竿放入电梯带回家中,如果竹竿恰好刚能放入电梯中(如图①示)那么,电梯的长、宽、高和的最大值是多少米?
(类比探究)为了解决这个实际问题,我们首先探究下面的数学问题.
探究:如图②,在中,.若,,,则与之有什么数量关系?
解:在中,
,
,即.
,
,
,
,
.
.
,,均大于,
与之间的数量关系是.
探究2:如图③,在四边形中,是对角线,,.若,,,,则与之间有什么数量关系?
解:,,
,.
,,,
,,.
将上面三式相加得,,
.
.
______.
,,,均大于,
与之间有这样的数量关系:______.
探究3:如图④,仿照上面的方法探究,在五边形中,,是对角线,,,.若,,,,,则与之间的数量关系是______.
(归纳结论)
当,,…,,时,若,则与之间的数量关系是__________.
(问题解决)
小明家住楼一天,他要把一根米长的竹竿放入电梯带回家中,如果竹竿恰好刚能放入电梯中(如图①示),那么,电梯的长、宽、高和的最大值是______米.
(拓展延伸)
公园准备修建一个四边形水池,边长分别为米,米,米,米,分别以水池四边为边向外建四个正方形花园,若花园面积和为平方米,则水池的最大周长为______米.
5.(2021·山东南区·九年级一模)(问题提出)用n个圆最多能把平面分成几个区域?
(问题探究)为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:如图1,一个圆能把平面分成2个区域.
探究二:用2个圆最多能把平面分成几个区域?
如图2,在探究一的基础上,为了使分成的区域最多,应使新增加的圆与前1个圆有2个交点,将新增加的圆分成2部分,从而增加2个区域,所以,用2个圆最多能把平面分成4个区域.
探究三:用3个圆最多能把平面分成几个区域?
如图3,在探究二的基础上,为了使分成的区域最多,应使新增加的圆与前2个圆分别有2个交点,将新增加的圆分成部分,从而增加4个区域,所以,用3个圆最多能把平面分成8个区域.
(1)用4个圆最多能把平面分成几个区域?
仿照前面的探究方法,写出解答过程,不需画图.
(2)(一般结论)用n个圆最多能把平面分成几个区域?
为了使分成的区域最多,应使新增加的圆与前个圆分别有2个交点,将新增加的圆分成______________部分,从而增加___________________个区域,所以,用n个圆最多能把平面分成__________________个区域.(将结果进行化简)
(3)(结论应用)
①用10个圆最多能把平面分成_________个区域;
②用___________个圆最多能把平面分成422个区域.
6.阅读材料:1261 年,我国南宋数学家杨辉著《详解九章算法》,在注释中提到“杨辉三角”解释了二项和的乘方规律.在他之前,北宋数学家贾宪也用过此方法,“杨辉三角”又叫“贾宪三角”.
这个三角形给出了(n 为正整数)的展开式(按a的次数由大到小的顺序、b的次数由小到大的顺序排列)的系数规律.例如:在三角形中第三行的三个数 1、2、1,恰好对应展开式中各项的系数;第四行的四个数 1、3、3、1,恰好对应展开式中各项的系数等.
从二维扩展到三维:根据杨辉三角的规则,向下进行叠加延伸,可以得到一个杨辉三角的立体图形.经研究,它的每一个切面上的数字所对应的恰巧是展开式的系数.
(1)根据材料规律,请直接写出的展开式;
(2)根据材料规律,如果将看成,直接写出的展开式(结果化简);若,求的值;
(3)已知实数a、b、c,满足,且,求的值.
7.先阅读下面的文字,然后按要求解题:
例:1+2+3+ … +100=?
如果一个一个顺次相加显然太繁琐,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法运算律,是可以大大简化计算,提高运算速度的.
因为1+100=2+99=3+98= … =50+51=101
所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+ … +100
=(1+100)+(2+99)+(3+98)+ … +(50+51)
=101×____________
=____________ .
(1)补全例题的解题过程;
(2)计算:
8.(2021·四川中区·九年级模拟预测)阅读与应用:
阅读1:a、b为实数,且a>0,b>0,因为,所以,从而(当a=b时取等号).
阅读2:函数(常数m>0,x>0),由阅读1结论可知: ,所以当即时,函数的最小值为.
阅读理解上述内容,解答下列问题:
问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为,周长为,求当x=__________时,周长的最小值为__________.
问题2:已知函数y1=x+1(x>-1)与函数y2=x2+2x+17(x>-1),当x=__________时,的最小值为__________.
问题3:某民办学习每天的支出总费用包含以下三个部分:一是教职工工资6400元;二是学生生活费每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
9.(2021·盐城市第一初级中学九年级月考)阅读材料:各类方程的解法:
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式,求解二元一次方程组,把它转化为一元一次方程来解;类似的,三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想——转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程的解是:=0,=______,=_______;
(2)拓展:用“转化”思想求方程的解;
(3)应用:如图,已知矩形草坪ABCD的长AD=21m,宽AB=8m,点P在AD上(AP>PD),小华把一根长为27m的绳子一段固定在点B,把长绳PB段拉直并固定在点P,再拉直,长绳的另一端恰好落在点C,求AP的长.
10.(2021·山东济南·九年级一模)阅读以下材料,并按要求完成相应的任务.
已知平面上两点,则所有符合且的点会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆.
阿氏圆基本解法:构造三角形相似.
(问题)如图1,在平面直角坐标中,在轴,轴上分别有点,点是平面内一动点,且,设,求的最小值.
阿氏圆的关键解题步骤:
第一步:如图1,在上取点,使得;
第二步:证明;第三步:连接,此时即为所求的最小值.
下面是该题的解答过程(部分):
解:在上取点,使得,
又.
任务:
将以上解答过程补充完整.
如图2,在中,为内一动点,满足,利用中的结论,请直接写出的最小值.
11.(2020·山东青岛·九年级一模)[提出问题]正多边形内任意一点到各边距离之和与这个正多边形的边及内角有什么关系?
[探索发现]
为了解决这个问题,我们不妨从最简单的正多边形-------正三角形入手
如图①,是正三角形,边长是是内任意一点,到各边距离分别为,确定的值与的边及内角的关系.
如图②,五边形是正五边形,边长是是正五边形内任意一点,到五边形各边距离分别为, 参照的探索过程,确定的值与正五边形的边及内角的关系.
类比上述探索过程:
正六边形(边长为)内任意一点 到各边距离之和
正八边形(边长为)内任意一点到各边距离之和
[问题解决]正边形(边长为)内任意-一点P到各边距离之和
12.(2020·青岛超银中学九年级月考)(问题情境)
我们知道若一个矩形是的周长固定,当相邻两边相等,即为正方形时,它的面积最大.反过来,若一个矩形的面积固定,它的周长是否会有最值呢?
(探究方法)
用两个直角边分别为,的4个全等的直角三角形可以拼成一个正方形。若,可以拼成如图所示的正方形,从而得到,即;当时,中间小正方形收缩为1个点,此时正方形的面积等于4个直角三角形面积的和.即.于是我们可以得到结论:,为正数,总有,当且仅当时,代数式取得最小值.另外,我们也可以通过代数式运算得到类似上面的结论:
∵,∴,
∴对于任意实数,总有,且当时,代数式取最小值.
使得上面的方法,对于正数,,试比较和的大小关系.
(类比应用)
利用上面所得到的结论完成填空
(1)当时,代数式有最 值为 .
(2)当时,代数式有最 值为 .
(3)如图,已知是反比例函数图象上任意一动点,,,试求的最小面积.
13.(2020·山西九年级一模)请阅读下列材料,并完成相应的任务.
梅涅劳斯(Menelaus)是公元一世纪时的希腊数学家兼天文学家,著有几何学和三角学方面的许多书籍.梅涅劳斯发现,三角形各边(或其延长线)被一条不过任何一个顶点也不与任何一条边平行的直线所截,这条直线可能与三角形的两条边相交(一定还会与一条边的延长线相交),也可能与三条边都不相交(与三条边的延长线都相交).他进行了深入研究并证明了著名的梅涅劳斯定理(简称梅氏定理):
设D,E,F依次是△ABC的三边AB,BC,CA或其延长线上的点,且这三点共线,则满足.
这个定理的证明步骤如下:
情况①:如图1,直线DE交△ABC的边AB于点D,交边AC于点F,交边BC的延长线与点E.
过点C作CM∥DE交AB于点M,则,(依据),
∴=,
∴BE•AD•FC=BD•AF•EC,即.
情况②:如图2,直线DE分别交△ABC的边BA,BC,CA的延长线于点D,E,F.
…
(1)情况①中的依据指: ;
(2)请你根据情况①的证明思路完成情况②的证明;
(3)如图3,D,F分别是△ABC的边AB,AC上的点,且AD:DB=CF:FA=2:3,连接DF并延长,交BC的延长线于点E,那么BE:CE= .
14.(2020·重庆八中九年级月考)请阅读下列材料:
问题:已知方程,求一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为,则,所以.
把代入已知方程,得
化简,得
故所求方程为.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式).
(1)已知方程,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为: .
(2)已知关于的一元二次方程有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数;
(3)已知关于的方程有两个实数根,求一个方程,使它的根分别是已知方程根的平方.
15.(2020·山东青岛·九年级期末)空间任意选定一点,以点为端点作三条互相垂直的射线,,.这三条互相垂直的射线分别称作轴、轴、轴,统称为坐标轴,它们的方向分别为(水平向前),(水平向右),(竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为,且的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体所在的面与轴垂直,所在的面与轴垂直,所在的面与轴垂直,如图所示.若将轴方向表示的量称为几何体码放的排数,轴方向表示的量称为几何体码放的列数,轴方向表示的量称为几何体码放的层数;如图是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了排列层,用有序数组记作 (1,2,6),如图的几何体码放了排列层,用有序数组记作 (2,3,4).这样我们就可用每一个有序数组表示一种几何体的码放方式.
(1)有序数组 (3,2,4)所对应的码放的几何体是_____;
(2)图是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为(___,____,____),组成这个几何体的单位长方体的个数为____个;
(3)为了进一步探究有序数组的几何体的表面积公式,某同学针对若干个单位长方体进行码放,制作了下列表格:
根据以上规律,请直接写出有序数组的几何体表面积的计算公式;(用表示)
(4)当时,对由个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(___,___,___),此时求出的这个几何体表面积的大小为________.(缝隙不计)最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
1
1
1
1个1
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
2
1
1
2个1
2
1
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
3
1
1
2个2
2
,
2
3
1
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
4
1
1
3个2
2
,
2
3
,
2
4
1
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
5
1
1
___
___
2
,
2
3
_______
_____
4
,
2
5
1
专题16 新定义问题的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1: 这是一份专题16 新定义问题的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1,文件包含专题16新定义问题的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题16新定义问题的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。
专题15 开放探究类的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1: 这是一份专题15 开放探究类的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1,文件包含专题15开放探究类的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题15开放探究类的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。
专题14 阅读理解类的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1: 这是一份专题14 阅读理解类的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1,文件包含专题14阅读理解类的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题14阅读理解类的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。












