专题05 有关平移、翻折、旋转等图形变换的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1

这是一份专题05 有关平移、翻折、旋转等图形变换的常见压轴题-【聚焦压轴】2022届中考数学压轴大题专项训练1，文件包含专题05有关平移翻折旋转等图形变换的常见压轴题解析版-聚焦压轴2022届中考数学压轴大题专项训练doc、专题05有关平移翻折旋转等图形变换的常见压轴题原卷版-聚焦压轴2022届中考数学压轴大题专项训练doc等2份试卷配套教学资源，其中试卷共50页， 欢迎下载使用。


专题5 有关平移、翻折、旋转等图形变换的常见压轴题
中考压轴大题5
1．（2021·北京市第五中学分校九年级月考）在平面直角坐标系中，正方形中，，，．给出如下定义：记线段的中点为，当点不在正方形上时，平移线段，使点落在正方形上，得到线段（，分别为点，的对应点）．线段长度的最小值称为线段到正方形的“平移距离”．
（1）已知点的坐标为，点在轴上．
①若点与原点重合，则线段到正方形的“平移距离”为______；
②若线段到正方形的“平移距离”为2，则点的坐标为______；
（2）若点，都在直线上，，记线段到正方形的“平移距离”为，求的最小值；
（3）若点的坐标为，，记线段到正方形的“平移距离”为，直按写出的取值范围．


【答案】（1）①；②（﹣5，0）或（7，0）；（2）；（3）．
【解题思路分析】（1）①根据题中的定义，观察发现线段AB到正方形MNPQ上最短距离是AG的长，然后可得到答案；
②当B在A左侧时，中点G到正方形的最短距离是线段AG的长；当B在A右侧时，中点G到正方形的最短距离是G到MQ的距离；
（2）如图3，连接ON并延长交直线y＝x+4于G，则GN即所求；
（3）由题可知，G在以A为圆心，半径是1的圆上，先求出d2最大值和最小值，然后就能确定范围．
【解析】解：（1）①如图1，

∵A的坐标为（﹣1，0），点B（0，0），
G是AB的中点，
∴AG＝＝，
∵线段AB到正方形MNPQ上最短距离是AG的长，
∴G到正方形MNPQ的“平移距离”为，
故答案为：；
②如图2，

当B在A左侧时，中点G到正方形的最短距离是线段AG的长，
∴AG＝2，
∴G（﹣3，0）
∴B（﹣5，0）
当B在A右侧时，中点G到正方形的最短距离是G到MQ的距离，
∴G（3，0），
∴B（7，0），
故答案为：（﹣5，0）或（7，0）；
（2）如图3，

连接ON并延长交直线y＝x+4于G，
则GN的长最短，
GN＝OG﹣ON＝，
∴d1最小值是；
（3）如图4，

∵，
∴G在以A为圆心，半径是1的圆上，
作AD⊥x轴于D，作GC⊥OD于C，
∴OA＝，
∴，
∴的最小值为，最大值为，
∴．
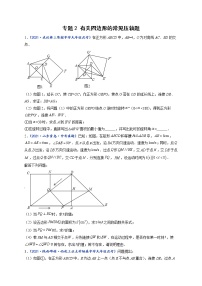
2．（2021·广州市第五中学九年级期中）如图，过原点的抛物线与轴交于点，为抛物线的顶点，连接，点是线段上的一个动点，过点作，垂足为点．

（1）将绕着点按顺时针方向旋转，得，当点落在抛物线上时，求点的坐标．
（2）当时，将线段绕平面某点旋转得到线段，若点、都落在抛物线上，求点和的坐标．
（3）当（1）中的点落在抛物线上时，将抛物线向左或向右平移个单位，点、平移后对应的点分别记为、，是否存在，使得以、、、为顶点的四边形周长最短？若存在，请直接写出的值和抛物线平移的方向，若不存在，请说明理由．

【答案】（1）（，0）；（2），；（3）存在，抛物线向左平移
【解题思路分析】（1），过点B作BQ⊥x轴于Q，过点作⊥于D，先证明△OQB是等腰直角三角形，得到∠BOP=45°，从而可以证明△OCP是等腰直角三角形，OC=CP，∠OPC=45°，设P（m，0），则，代入抛物线解析式求解即可；
（2）过点C作CD⊥OA于D，求出C（1，1），将线段PC绕平面某点旋转180°得到线段EF，设这个点的坐标为（a，b），则，，从而得到，，再根据E、F在抛物线上，求解即可；
（3）将沿平移，使得与B点重合，点A落在处，，以过B的直线y=2为对称轴，作的对称点，连接，当点M为与直线y=2的交点时，此时以O、M、N、A为顶点的四边形周长最短，先求出，则，再求出M的坐标即可得到答案．
【解析】解：（1）如图所示，过点B作BQ⊥x轴于Q，过点作⊥于D，

∵点B是抛物线的顶点，
∴B（2，2），
∴OQ=BQ=2，
∴△OQB是等腰直角三角形，
∴∠BOP=45°，
又∵PC⊥OB，
∴∠OCP=90°，
∴△OCP是等腰直角三角形，
∴OC=CP，∠OPC=45°，
由旋转的性质可得，，，
设P（m，0），则，
∴，
∴
∵在抛物线上，
∴即，
解得或（舍去），
∴P（，0）；
（2）如图所示，过点C作CD⊥OA于D，

∵B（2，2），PB⊥OA，
∴OP=PB=2，△OBP为等腰直角三角形，P（2，0），
由（1）得PC=OC，
∵，
∴，
∴，
又∵CD⊥OA，
∴OD=CD=PD=1，
∴C（1，1），
将线段PC绕平面某点旋转180°得到线段EF，设这个点的坐标为（a，b），
∴，，
∴，，
∴，，
又∵E、F都在抛物线上，
∴，
∴
解得
∴，；
（3）存在，抛物线向左平移，理由如下：
由（1）可知，如图将沿平移，使得与B点重合，点A落在处，，以过B的直线y=2为对称轴，作的对称点，连接，当点M为与直线y=2的交点时，此时以O、M、N、A为顶点的四边形周长最短，

∵A是抛物线与x轴的交点，
∴A（4，0）
∵，且，，B（2，2），
∴，
∴，
设直线的解析式为，
∴，
解得，
∴直线的解析式为，
∵M在直线y=2上，
∴，
解得，
∴
∴，
∴存在，抛物线向左平移．
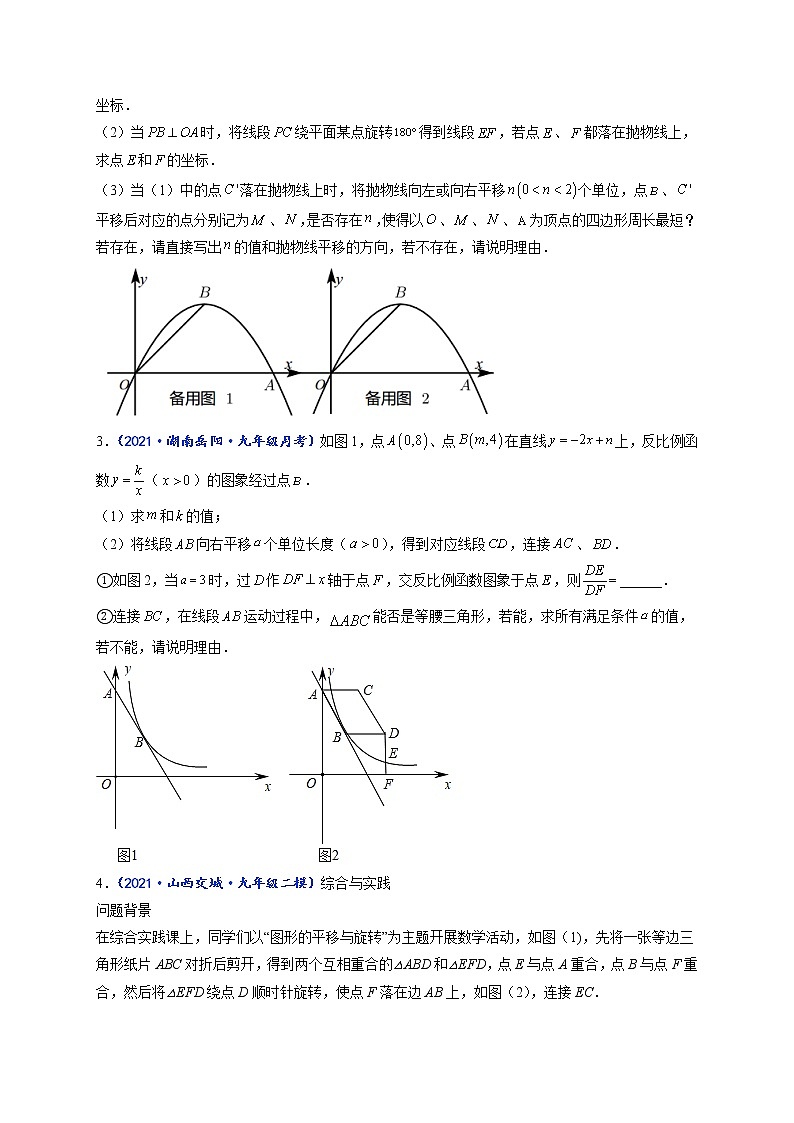
3．（2021·湖南岳阳·九年级月考）如图1，点、点在直线上，反比例函数（）的图象经过点．
（1）求和的值；
（2）将线段向右平移个单位长度（），得到对应线段，连接、．
①如图2，当时，过作轴于点，交反比例函数图象于点，则______．
②连接，在线段运动过程中，能否是等腰三角形，若能，求所有满足条件的值，若不能，请说明理由．

【答案】（1），；（2）①，②能，4或5或
【解题思路分析】（1）先将点A坐标代入直线AB的解析式中，求出n，进而求出点B坐标，再将点B坐标代入反比例函数解析式中即可得出结论；
（2）①先确定出点D（5，4），进而求出点E坐标，进而求出DE，EF，即可得出结论；②先表示出点C，D坐标，再分三种情况：Ⅰ、当BC=CD时，判断出点B在AC的垂直平分线上，即可得出结论；Ⅱ、当BC=BD时，先表示出BC，用BC=BD建立方程求解即可得出结论；Ⅲ、当时，同理建立方程求解即可得出结论．
【解析】解：（1）∵点A(0，8)在直线上，
∴，
∴，
∴直线的解析式为，
将点B(m，4)代入直线的解析式上，得，
∴，
∴B(2，4)，
将B(2，4)代入反比例函数解析式中，得；
（2）①由（1）知，B(2，4)，，

∴反比例函数解析式为，
当时，
∴将线段向右平移3个单位长度，得到对应线段，
∴D（2+3，4），即：D（5，4），
∵轴于点，交反比例函数图象于点，
∴E(5，)，
∴，，
∴；
②如图，

∵将线段向右平移个单位长度（），得到对应线段，
∴，，
∵A(0，8)，B(2，4)，
∴C(a，8)，
∵是等腰三角形，
∴Ⅰ、当时，
∴点在线段的垂直平分线上，
∴；
Ⅱ、当时，
∵B(2，4)，C(a，8)，
∴，
∴，
∴；
Ⅲ、当时，
∴，
即：是等腰三角形时，满足条件的值为4或5或．
4．（2021·山西交城·九年级二模）综合与实践
问题背景
在综合实践课上，同学们以“图形的平移与旋转”为主题开展数学活动，如图（1)，先将一张等边三角形纸片ABC对折后剪开，得到两个互相重合的△ABD和△EFD，点E与点A重合，点B与点F重合，然后将△EFD绕点D顺时针旋转，使点F落在边AB上，如图（2），连接EC．　　　
　　　
操作发现
（1）判断四边形BFEC的形状，并说明理由；
实践探究
（2）聪聪提出疑问：若等边三角形的边长为8，将图（2）中的△EFD沿射线BC的方向平移a个单位长度，得到△E′F′D′，连接BF′，CE′，若四边形BF′E′C为菱形，如图（3），则a的值为多少？请你帮聪聪解决这个问题，求出a的值；
（3）如果将（2）中聪聪所提问题的平移方向改为：沿射线CB的方向平移a个单位长度，其余条件都不变，则是否还存在四边形BF′E′C为菱形？若存在，直接写出平移距离a的值，若不存在，请说明理由；
（4）老师提出问题：请参照聪聪的思路，若等边三角形的边长为8，将图（2）中的△EFD在平面内进行一次平移，得到△E"F"D"，请在图（4）中画出平移后构造出的新图形，标明字母，说明平移及构图方法，写出你发现的一个结论，不必证明．
【答案】（1）四边形BFEC为平行四边形，理由见解析；（2）a=2-2 （3）存在，a=2+2；（4）答案不唯一，合理即可给分．
【解题思路分析】（1）由等边三角形的性质及旋转的性质得△BFD为等边三角形，从而得EF∥BC且EF=BC，根据一组对边平行且相等的四边形是平行四边形即可得结论；
（2）过点E′作E′G垂直BC交BC的延长线于点G，根据菱形的性质和解直角三角形分别求得E′G、D′G、CG的长度，从而可求得a的值；
（3）过点F′作F′G垂直BC交CB的延长线于点G，余下与（2）同；
（4）由于没有限制，只要合理即可．
【解析】（1）四边形BFEC为平行四边形。
理由如下：∵△ABC为等边三角形
∴∠ABD=60°，AB=BC
由题意，知FD=BD
∴△BFD为等边三角形
∴∠FDB=60°
∵∠EFD=60°
∴EF∥BC
∵EF=AB=BC
∴四边形BEFC为平行四边形
（2）在Rt△ABD中，∠ABD=60°，BD=BC=4
∴AD=4
当△DEF沿射线BC方向平移时，过点E′作E′G垂直BC交BC的延长线于点G

∵E′F′ ∥BC， ∠F′E′D′=30°
∴∠E′D′ G=30°
在Rt△E′D′G 中，E′D′=4
∴E′G=2
∴D′G=6
∵四边形BF′E′C为菱形。
∴CE′=8
在Rt△E′CG中，由勾股定理得CG=2
∴DG=DC+CG=4+2
∴DD′=DG-D′G=2-2
∴a=2-2
（3）存在
当△DEF沿射线CB方向平移时，过点F′作F′G垂直BC交CB的延长线于点G，如图

∵E′F′ ∥BC， ∠F′E′D′=30°
∴∠E′D′ C=30°
∵∠F′D′E′=90°
∴∠F′D′G=60°，
∴∠D′F′ G=30°
在Rt△F′D′G 中，F′D′=FD=4
∴D′G=2
∴F′G=2
若四边形BF′E′C为菱形，则BF′=8
在Rt△F′BG中，由勾股定理得BG=2
∴DG=BD+BG=4+2
∴DD′=DG-D′G=2+2
∴a=2+2
（4）将△EFD沿FA方向平移4个单位长度，得到△E"F"D"，则D"是AC的中点，所以DF=FA，且四边形AFD D"是平行四边形，从而四边形AFD D"是菱形．

5．（2021·辽宁铁西·九年级一模）如图，在平面直角坐标系中，直线与轴交于点，直线与轴交于点，与轴交于点，与直线交于点．

（1）求点的坐标；
（2）将沿轴向左平移，平移后点的对应点为点，点的对应点为点，点的对称点为点，当点到达点时，停止平移，设平移的距离为．
①当点在直线上时，求的面积；
②当与四边形重合部分的面积为2时，请直接写出的值．
【答案】（1）点的坐标为；（2）①；②1或
【解题思路分析】（1）解方程，即可求D的坐标；
（2）①先求出O，B，C各点的坐标，然后根据点的平移t设G，F，E三点的坐标，根据点G在直线y＝2x+6上求出G点坐标，利用面积公式可求出△DCG的面积；
②首先计算△EFG的面积，判断当点G在直线y＝2x+6上时，E点的位置，及点F达到点A是，G点的位置．进而判断何时△EFG与四边形AOCD重合部分的面积为2，然后求解．
【解析】解：（1）∵直线y＝﹣2x+3与直线y＝2x+6交于点D，
由，得
；
∴点D的坐标为（，）；
（2）当x＝0时，y＝2×0+6＝6，y＝﹣2×0+3＝3；
当y＝0时，2x+6＝0，﹣2x+3＝0；解得x＝﹣3，x；
点O（0，0），A（﹣3，0），B（，0），C（0，3）；
由平移的距离为t知，点E（，0），点F（﹣t，0），点G（﹣t，3）；
①当点G在直线y＝2x+6上时，得3＝2×（﹣t）+6，解得t；
∴点G坐标为（，3）；
∴GC；
S△DGC•（yD﹣yc）；
②；
当点G在直线y＝2x+6上时，
FE＝OBFD，
O，E重合，
△GFE完全在四边形AOCD内，
此时S△GFE＝S△COB；即重合部分面积为；
此时，t，
1°当t时，GE与y轴交于M，
此时△EFG与四边形AOCD重合部分的为四边形GFOM，面积为2．
即S△MOE+S四边形GFOM，
∴S△MOES四边形GFOM；
∵OM∥GF
∴△MOE∽△GFE
∴
∴OE；
即t＝BO﹣OE＝1；

2°当t时，GE与y＝2x+6交于N，GF与y＝2x+6交于N，
此时△EFG与四边形AOCD重合部分的为四边形QFEN，面积为2
此时；
设直线GE解析式：y＝﹣2x+b；
把E（，0）代入得y＝﹣2x+b，解得b＝3﹣2t；
直线GE解析式：y＝﹣2x+3﹣2t；
解方程得；
；
∴点N坐标为（，）；
把x＝﹣t代入y＝2x+6，得y＝﹣2t+6，
GQ＝3﹣（﹣2t+6）＝2t﹣3，
S△GNQGQ•|yG﹣yN|•（t）
解得t或t（舍去）；
∴t＝1，或t．

6．（2021·江苏盱眙·九年级期中）（问题情境）
如图1，在中，，AD⊥BC于点D，，，求AD的长．
（问题解决）
小明同学是这样分析的：将沿着AB翻折得到，将沿着AC翻折得到，延长EB、FE相交于点G，请按着小明的思路解答下列问题：
（1）由上可得四边形AEGF是　 　（填矩形、菱形、正方形中的一个）；
（2）在中运用勾股定理，求出AD的长．
（方法提炼）通过问题解决，小明发现翻折是解决问题的有效办法之一，它可以将问题中的相关信息有效地集中、关联与重组．请根据自己的理解，解答下列问题：
（3）如图2，在四边形ABCD中，，，，，求AC的最大值．
（4）如图3，在四边形ABCD中，，AD＝2，M是AB上一点，且，，，直接写出CD的最大值为　 　．

【答案】（1）正方形；（2）12；（3）；（4）
【解题思路分析】（1）先根据，，得出，再根据垂直，，由此可证得四边形是矩形，最后再根据全等三角形的性质可证得，由此即可证得四边形是正方形；
（2）利用勾股定理，建立关于的方程模型，求出即可；
（3）将沿着AB翻折得到，将沿着AD翻折得到，连接EF，结合翻折的性质以及可得，进而可求得，再利用勾股定理可求得，最后根据当BE、BD、DF三条线段共线时，EF取得最大为24，由此即可求得AC的最大值；
（4）将沿着DM翻折得到，将沿着CM翻折得到，连接EF，结合翻折的性质以及可得，进而可求得，最后根据CD≤DE＋EF＋FC＝，当点D、E、F、C在同一直线上时取得最大值，由此即可求得答案．
【解析】解：（1）四边形AEGF是正方形，理由如下：
由折叠得：，．
，，
又∵，
．
又，
，．
四边形是矩形，
∵，，
∴，，
．
矩形是正方形，
故答案为：正方形；
（2）设，则．
，，
，，
，，
在中，，
．
化简得，，
解得：，（舍去）
∴；
（3）如图①，将沿着AB翻折得到，将沿着AD翻折得到，连接EF，

∴BE＝BC＝6，DF＝CD＝8，且AE＝AF＝AC，，，
又∵，
．
∴，
∵，，，
∴，
∵当BE、BD、DF三条线段共线时，EF最大，
∴EF的最大值为6＋8＋10＝24，
∴AC的最大值为；
（4）如图②，将沿着DM翻折得到，将沿着CM翻折得到，连接EF，

由翻折可得：DE＝AD＝2，EM＝AM＝3，MF＝BM＝4，CF＝BC＝，，，
∵，
∴，
∴，
∴，
∵EM＝3，MF＝4，
∴，
∵CD≤DE＋EF＋FC＝，当点D、E、F、C在同一直线上时取得最大值，
∴CD的最大值为，
故答案为：．
7．（2021·山东中区·九年级期末）定义：关于x轴对称且对称轴相同的两条抛物线叫作“同轴对称抛物线”．例如：y1＝（x﹣1）2﹣2的“同轴对称抛物线”为y2＝﹣（x﹣1）2+2．
（1）请写出抛物线y1＝（x﹣1）2﹣2的顶点坐标 ；及其“同轴对称抛物线”y2＝﹣（x﹣1）2+2的顶点坐标 ；
（2）求抛物线y＝﹣2x2+4x+3的“同轴对称抛物线”的解析式．
（3）如图，在平面直角坐标系中，点B是抛物线L：y＝ax2﹣4ax+1上一点，点B的横坐标为1，过点B作x轴的垂线，交抛物线L的“同轴对称抛物线”于点C，分别作点B、C关于抛物线对称轴对称的点、，连接BC、、、．
①当四边形为正方形时，求a的值．
②当抛物线L与其“同轴对称抛物线”围成的封闭区域内（不包括边界）共有11个横、纵坐标均为整数的点时，直接写出a的取值范围．

【答案】（1）(1，﹣2)，(1，2)；（2）y＝2（x﹣1）2﹣5；（3）①a＝；②≤a≤1或﹣≤a＜﹣
【解题思路分析】（1）根据顶点式y＝a（x﹣h）2+k的顶点坐标为（h，k）；
（2）先化成顶点式，再求“同轴对称抛物线”的解析式；
（3）①写出点B的坐标，再由对称轴求出点B'，然后结合正方形的性质列出方程求 a；
②先由对称性分析得到封闭区域内在x轴上整点的个数，然后针对抛物线L开口的不同进行分类讨论．
【解析】解：（1）由y1＝（x﹣1）2﹣2知顶点坐标为（1，﹣2），
由y2＝﹣（x﹣1）2+2知顶点坐标为（1，2），
故答案为：（1，﹣2），（1，2）．
（2）∵y＝﹣2x2+4x+3y＝﹣2（x﹣1）2+5，
∴“同轴对称抛物线”的解析式为：y＝2（x﹣1）2﹣5．
（3）①当x＝1时，y＝1﹣3a，
∴B（1，1﹣3a），
∴C（1，3a﹣1），
∴BC＝|1﹣3a﹣（3a﹣1）|＝|2﹣6a|，
∵抛物线L的对称轴为直线x＝＝2，
∴点B'（3，1﹣3a），
∴BB'＝3﹣1＝2，
∵四边形BB'C'C是正方形，
∴BC＝BB'，即|2﹣6a|＝2，
解得：a＝0（舍）或a＝．
②抛物线L的对称轴为直线x＝2，顶点坐标为（2，1﹣4a），
∵L与“同轴对称抛物线”关于x轴对称，
∴整点数也是关于x轴对称出现的，
∴封闭区域内在x轴上的整点可以是3个或5个，L与x轴围成的区域内整点个数为4个或3个，
（i）当a＞0时，
∵L开口向上，与y轴交于点（0，1），
∴封闭区域内在x轴上只可能有3个整点，两个区域内各有4个整点，
∴当x＝1时，﹣2≤1﹣3a＜﹣1，当x＝2时，﹣3≤1﹣4a＜﹣2，
解得：≤a≤1；
（ii）当a＜0时，
∵L开口向下，与y轴交于点（0，1），
∴封闭区域内在x轴上只可能有5个整点，两个区域内各有3个整点，
∴当x＝2时，1＜1﹣4a≤2，当x＝﹣1时，5a+1＜0，
解得：，
综上所述：≤a≤1或﹣≤a＜﹣．
8．（2021·湖北当阳·九年级一模）如图，在矩形中，，，点是边上的点（不与点，重合），将沿折叠，点是点的对应点；点是边上的点，将沿折叠，点是点的对应点，且点在直线上．

（1）若，求的长；
（2）若点是的中点，求的值；
（3）当点恰好落在边上时，求四边形的面积．
【答案】（1）1；（2）或；（3）或
【解题思路分析】（1）先由折叠可得推导出，然后可证明≌（AAS），即可求解的长；
（2）由（1）得知，∽，根据相似三角形对应边成比例，可求的长，则可求解；
（3）先证明≌（AAS），然后能证明四边形是平行四边形，设，，可知，，，在中，，再由∽，得，求出，则可求解面积．
【解析】解：（1）将沿折叠，点是点的对应点，
∴≌，
∴，
∵将沿折叠，点是点的对应点，
∴≌，
∴，
∴，
∵，
∴，
∵，
∴≌（AAS），
∴，，
∵，，
∴，，
∴；
（2）由（1）知，∽，
∴，
∵点是的中点，
∴，
∴，
∴或，
在中，或；
（3）连接，交于点，

∵点恰好落在边上，
∴是的垂直平分线，
∴，
∴，
∵，
∴，
∵，，
∴≌（AAS），
∴，
∴，
∵，
∴四边形是平行四边形，
设，，
则，，，
在中，，
∴，
∵∽，
∴，
∴，
∴，
解得，
∴四边形的面积,
综上：四边形的面积为或．
9．（2021·湖北襄阳·中考真题）在中，，，是边上一点，将沿折叠得到，连接．
（1）特例发现：如图1，当，落在直线上时，
①求证：；
②填空：的值为______；
（2）类比探究：如图2，当，与边相交时，在上取一点，使，交于点．探究的值（用含的式子表示），并写出探究过程；
（3）拓展运用：在（2）的条件下，当，是的中点时，若，求的长．


【答案】（1）①见解析；②1；（2），见解析；（3）
【解题思路分析】（1）①根据折叠性质证明即可；②当，证明，即可得出的值；
（2）延长交于点，根据折叠性质证明，即可得出结论；
（3）由（2）可知，设，则，，，可得，再由勾股定理列方程求解即可．
【解析】解：（1）①证明：延长交于点．

由折叠得．
∴．
∵，
∴．
②当，即时，
可知AC=BC，
在和中，
，
∴(AAS)，
∴，
∴．
故答案为：1；
（2）解：．
理由：延长交于点，

由折叠得．
∴，
∵，
∴，
∵，
∴，
∴．
（3）解：由折叠得，，
∵是的中点，
∴，
∴，，，
由（2）知，
∴，
，
是的中点，
∴，
∴，
设，则，，，
∴，

∴，
∴，，
∴，
在中，由勾股定理得，
∵，
∴，
解得（负值舍去），
∴．
10．（2021·河北竞秀·九年级一模）如图，平行四边形ABCD中，AB＝9，AD＝13，tanA＝，点P在射线AD上运动，连接PB，沿PB将△APB折叠，得△A'PB．

（1）如图1，点P在线段AD上，当∠DPA'＝20°时，∠APB＝　 　度；
（2）如图2，当PA'⊥BC时，求线段PA的长度；
（3）当点A'落在平行四边形ABCD的边所在的直线上时，求线段PA的长度；
（4）直接写出：在点P沿射线AD运动过程中，DA′的最小值是多少？
【答案】（1）80或100；（2）线段PA的长度为；（3）线段PA的长度为或9或；（4）DA′的最小值是．
【解题思路分析】（1）分两种情况讨论，当在直线的右侧时，或当在直线的左侧时，再根据折叠的性质解题即可；
（2）作于，由正切定义设，根据勾股定理解得，由此解得的值，再根据题意解题；
（3）分三种情况讨论，①当点在上时，②当点在上时，③当点在的延长线上时，分别画出相应的示意图，再根据正切的定义或菱形的性质解题即可；
（4）作于，连接，由勾股定理解得的长，再利用三角形三边关系解题．
【解析】解：（1）当在直线的右侧时，
△APB折叠得到△A'PB，

当在直线的左侧时，
，
故答案为：80或100；
（2）如图，作于，

平行四边形ABCD中，






设，





；
（3）①当点在上时，




；
②当点在上时，

由折叠可知，



四边形是菱形，
；
③当点在的延长线上时，


综上所述，线段PA的长度为或9或；
（4）如图，作于，连接，







的最小值是．
11．（2021·浙江杭州·九年级期末）如图，在⊙O中，为⊙O的直径，弦，垂足在半径上．若劣弧沿着直线翻折，点落在上的点处（点不与点重合），连结．

（1）求证：．
（2）延长交⊙O于点，连结，若，求的正弦值．
【答案】（1）见解析；（2）
【解题思路分析】（1）由折叠的性质可得∠ECH=∠BCH，由圆周角定理可得∠ACB=90°，即∠BCH+∠ACH=90°，利用垂径定理易得CD⊥AB，即∠CAO+∠ACH=90°，等量代换可得结果；
（2）由折叠的性质可得∠B=∠CEB，EH=BH，利用圆周角定理可得∠B=∠AMC，定量代换可得∠AMC=∠AEM，易得AE=AM=10，又因为OC=OA，可得3+OH=13-OH，可得OH，利用边角关系可得结果．
【解析】解：（1）证明：连接CO，

由翻折可知∠ECH=∠BCH，
∵OA=OC,
∴∠CAO=∠ACO，
∵AB为⊙O的直径，
∴∠ACB=90°，
∴∠BCH+∠ACH=90°，
∵CD⊥AB，
∴∠CAO+∠ACH=90°，
∴∠BCH=∠CAO=∠ACO，
∴∠ECH=∠ACO，
即∠ACE+∠ECO=∠DCO+∠ECO，
∴∠ACE=∠DCO．
（2）连接CO，

由翻折可知∠B=∠CEB，EH=BH，
∵∠B=∠AMC，∠CEB=∠AEM，
∴∠AMC=∠AEM，
∴AE=AM=10，
∴OC=OA=13，
∴3+OH=13-OH，
∴OH=5，
∴sin∠ACE=sin∠DCO=．
12．（2021·洛阳市实验中学九年级月考）如图1，菱形绕点顺时针旋转，得到菱形，连接，、分别与，相交于点，．射线，交于点，．
（1）当时，四边形的形状为 ．
（2）求与的数量关系．
（3）如图2．连接，若，，求的值．
（4）如图3，连接，，若，，四边形能否为菱形？若能，直接写出的值和的长；若不能，请说明理由．

【答案】（1）正方形；（2）α+β=180°；（3）α=96°；（4）能，α的值为120°，AP的长为2．
【解题思路分析】（1）由旋转的性质得到AO=AO′，∠OAO′=90°，由菱形的性质得到∠POA=∠AO′P=90°，可以推出四边形AOPO′为正方形；
（2）利用旋转的性质推出∠AEP+∠AEG=∠AEP+∠ABD=180°，再结合四边形的内角和即可推出结论；
（3）结合已知条件可分别先求出各部分角度，然后结合旋转的性质推出∠BPG的度数，再结合（2）的结论求解即可；
（4）利用勾股定理即可求得AO的长，根据菱形的性质推出BD是AC的垂直平分线，证明△PAC是等边三角形，即可求解．
【解析】：（1）当α=90°时，四边形AOPO′的形状为正方形．

∵菱形AEFG是菱形ABCD旋转得到的，且点O，O′是对角线的交点，
∴AO=AO′，∠OAO′=90°，∠POA=∠AO′P=90°，
∴四边形AOPO′为正方形，
故答案为：正方形；
（2）由题意△BAD≌△EAG，
∴∠ABD=∠AEG，
∵射线BD，GE交于点P，

∴∠AEP+∠AEG=∠AEP+∠ABD=180°，
在四边形ABPE中，∠BAE+∠BPG =360°-（∠AEP+∠ABD）=180°，
∴∠BAE=a，∠BPG=β，
∴α+β=180°；
（3）由菱形的性质知，AB=AD，△ABD为等腰三角形，

∴当∠BAD=42°时，∠ABD=∠ADB=69°，
∵PA=PB，
∴∠ABP=∠BAP=69°，
∴∠BPA=42°，
∵AO=AO′，
∴PA平分∠BPG，即：∠BPA=∠GPA=42°，
∴∠BPG=84°，即：β=84°，
由①知：α +β=180°，
∴α=180°-84°=96°；
（4）能，理由如下：
连接PA，

∵四边形ABCD是菱形，且对角线交点为O，AB=5，BD=4，
∴BO=DO=2，AO=CO，∠BOA=90°，
∴AO=CO=，
∴AC=2，
同理： 由旋转对称性可得
当时，
四边形AFPC是菱形，
∵四边形ABCD是菱形，
∴BD是AC的垂直平分线，
∴PC=PA，
∴△PAC是等边三角形，
∴PA=PC=2，∠PAC=60°，
∴∠CAF=120°，
即α的值为120°，AP的长为2．
13．（2021·浙江鹿城·九年级月考）如图1是实验室中的一种摆动装置，BC在地面上，支架ABC是底边为BC的等腰直角三角形，摆动臂AD可绕点A旋转，摆动臂DM可绕点D旋转，AD=30，DM=10

（1）在旋转过程中，
①当A，D，M三点在同一直线上时，求AM的长；
②当A，D，M三点为同一直角三角形的顶点时，求AM的长
（2）若摆动臂AD顺时针旋转90°，点D的位置由△ABC外的点D1转到其内的点D2处，连结D1D2，如图2．此时∠AD2C=135°，CD2=60，求BD2的长．
【答案】（1）①40或20；②20或10；（2）30
【解题思路分析】（1）①分两种情形分别求解即可．
②显然不能为直角．当为直角时，根据，计算即可，当时，根据，计算即可．
（2）连接．首先利用勾股定理求出，再利用全等三角形的性质证明即可．
【解析】解：（1）①，或．
②显然不能为直角．
当为直角时，，
或舍弃）．
当时，，
或舍弃）．
综上所述，满足条件的的值为或．
（2）如图2中，连接．

由题意：，，
，，
，
，
，
，
，
，
，，
，
．
14．（2021·辽宁鞍山·九年级期末）如图，抛物线y＝x2+bx+c经过点B（﹣2，0）和点C（0，﹣2），与x轴交于点A．

（1）求抛物线的解析式；
（2）点P（0，n）是y轴上的一个动点，将线段OB绕点P顺时针旋转90°，得到线段O'B'；
①若线段O'B'与抛物线有一个公共点，结合函数图象，请直接写出n的取值范围；
②直线PB'交抛物线于M、N两点，若点B'是线段MN的中点，求n的值．
【答案】（1）y=x2﹣x﹣2；（2）①线段O'B'与抛物线有一个公共点时，1﹣≤n≤﹣2或4≤n≤1+；②．
【解题思路分析】（1）将点B（-2，0）和点C（0，-2）代入抛物线y=x2+bx+c，即可求解析式；（2）①由题可知O'（-n，n），B'（-n，n+2），当O'在抛物线上时，n2+n-2=n，求出n=4或n=-2；当B'在抛物线上时，n2+n-2n=2，求出n=1+或n=1-，再结合函数图象即可确定n的取值范围；
②求出PB'的解析式为y=-x+n，联立-x+n=x2-x-2，由根与系数的关系得xM+xN=2-，又由B'是MN的中点，则xM+xN=-2n，所以2-=-2n，即可求出n=-1±．
【解析】解：（1）将点B（-2，0）和点C（0，-2）代入抛物线y=x2+bx+c，
得，解得，
∴y=x2x-2；
（2）①由题意可知O'（-n，n），B'（-n，n+2），
当n＞0时，如图1，

当O'在抛物线上时，n2+n-2=n，
解得n=4或n=-2（舍），
当B'在抛物线上时，n2+x-2n=2，
解得n=1+或n=1-（舍），
∴当4≤n≤1+时线段O'B'与抛物线有一个公共点；
当n＜0时，如图2，

当O'在抛物线上时，n2+n-2=n，
解得n=4（舍）或n=-2，
当B'在抛物线上时，n2+n-2n=2，
解得n=1+（舍）或n=1-，
∴当1-≤n≤-2时线段O'B'与抛物线有一个公共点；
综上所述：线段O'B'与抛物线有一个公共点时，1-≤n≤-2或4≤n≤1+；
②设PB'的解析式为y=kx+b，
则有，
解得，
∴y=x+n，
联立x+n=x2-x-2，
∴x2+（-2）x-（8+4n）=0，
∴xM+xN=2-，
∵B'是MN的中点，
∴xM+xN=-2n，
∴2-=-2n，
∴n=．
15．（2021·沈阳实验中学九年级二模）如图1，直线交x轴于点A，交y轴于点，抛物线经过点A，交y轴于点，点P为地物线上一个动点，过点P作x轴的垂线，过点B作于点D，连接，设点P的横坐标为m．
（1）求抛物线的解析式；
（2）当为等腰直角三角形时，求线段的长；
（3）如图2，将绕点B逆时针旋转到，且旋转角当点P的对应点落在x轴上时，请直接写出点P的坐标．

【答案】（1）y=-2；（2）当△BPD为等腰直角三角形时，PD的长为或；（3），，．
【解题思路分析】（1）先求得点A的坐标，再利用待定系数法求抛物线的解析式即可；
（2）设点P的横坐标为m,可得P（m，-2），D（m，-2），若△BPD为等腰直角三角形，则PD=BD.分两种情况：①当点P在直线BD的上方时，PD=,再分点P在y轴的左侧和右侧两种情况，列方程求解即可；②当点P在直线BD的下方时，m＞0，BD=m，PD=,列方程求解即可；
（3）由∠PBP/=∠OAC，OA=3，OC=4；由勾股定理可得AC=5，继而可得sin∠PBP/=，cos∠PBP/=，然后分 点P/落在x轴上和点P/落在y轴上两种情况分别讨论求解即可．
【解析】解：（1）由直线y=x+n过点C（0,4），得n=4，
∴y=x+4，
当y=0时，0=x+4，
解得x=3，
∴A（3，0），
∵抛物线y=+c经过点A（3,0），B（0，-2），
∴ ，
解得，
∴y=-2；
（2）设点P的横坐标为m，
∴P（m，-2），D（m，-2）；
若△BPD为等腰直角三角形，则PD=BD，
①当点P在直线BD的上方时，PD=,
（Ⅰ）若点P在y轴的左侧，则m＜0，BD=-m，
∴=-m，
解得m1=0（舍去），m2=（舍去），
（Ⅱ）若点P在y轴的右侧，则m＞0，BD=m，
∴=m，
解得m1=0（舍去），m2=，

②当点P在直线BD的下方时，m＞0，BD=m，PD=，
∴=m，
解得m1=0（舍去），m2=，

综上m=或；
即当△BPD为等腰直角三角形时，PD的长为或；
（3）∵∠PBP/=∠OAC，OA=3，OC=4，
∴AC==5，
∴sin∠PBP/=，cos∠PBP/=；
①当点P/落在x轴上时，过点D/作D/N⊥x轴于N，交BD于点M，∠DBD/=∠ND/P/=∠PBP/，
如图，ND/-MD/=2，点P在y轴左侧，m＜0，
∵P′D′=PD=，BD′=BD=-m，
∴D′N=P′D′，∠MBD′+∠MD′B=90°，∠P′D′N+∠MD′B=90°，
∴∠P′D′N=∠D′BD，
∴D′N=P′D′cos∠P′D′N=，D′M=BD′sin∠D′BD=-m
即×（m2-m）-（-m）=2；
解得m=-，m=（舍），
y=，
P（－，），

如图，ND/+MD/=2，点在y轴右侧，
∵∠P′D′B=90°，
∴∠P′D′N+∠BD′M=90°，∠BD′M+∠MBD′=90°，
∴∠P′D′N=∠MBD′,
∵P′D′=PD=，BD′=BD=m，
∴MD′=BDsin∠D′BD=m，ND′=P′D′cos∠P′D′N×（m2-m），
即×（m2-m）+m=2，
解得m=，m=-(舍)，
当m=时，y=，
解得： P（，）；

②当点P/落在y轴上时，
如图，过点D/作D/M⊥x轴交BD于点M，过点P/作P/N⊥y轴，交MD/的延长线于点N，
∵∠P′D′B=90°，
∴∠P′D′N+∠BD′M=90°，∠BD′M+∠MBD′=90°，
∴∠P′D′N=∠MBD′,
∠DBD/=∠P/D/N =∠PBP/,
∵PN=BM，P′N=P′D′sin∠P′D′N=×（m2-m），BM=BD′cos∠D′BD=m，
∴×（m2-m）=m，
解得：或（舍），
当时，y=，
∴P（，）．

综上，，，．
16．（2021·山东日照·中考真题）问题背景：
如图1，在矩形中，，，点是边的中点，过点作交于点．

实验探究：
（1）在一次数学活动中，小王同学将图1中的绕点按逆时针方向旋转，如图2所示，得到结论：①_____；②直线与所夹锐角的度数为______．
（2）小王同学继续将绕点按逆时针方向旋转，旋转至如图3所示位置.请问探究（1）中的结论是否仍然成立？并说明理由．
拓展延伸：
在以上探究中，当旋转至、、三点共线时，则的面积为______．
【答案】（1），30°；（2）成立，理由见解析；拓展延伸：或
【解题思路分析】（1）通过证明，可得，，即可求解；
（2）通过证明，可得，，即可求解；
拓展延伸：分两种情况讨论，先求出，的长，即可求解．
【解析】解：（1）如图1，，，，
，
如图2，设与交于点，与交于点，

绕点按逆时针方向旋转，
，
，
，，
又，
，
直线与所夹锐角的度数为，
故答案为：，；
（2）结论仍然成立，
理由如下：如图3，设与交于点，与交于点，

将绕点按逆时针方向旋转，
，
又，
，
，，
又，
，
直线与所夹锐角的度数为．
拓展延伸：如图4，当点在的上方时，过点作于，

，，点是边的中点，，
，，，
，，
，
、、三点共线，
，
，
，
，
由（2）可得：，
，
，
的面积；
如图5，当点在的下方时，过点作，交的延长线于，

同理可求：的面积；
故答案为：或．