初中数学冀教版八年级下册第二十章 函数综合与测试复习练习题

冀教版八年级数学下册第二十章函数综合练习

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、下列函数中，自变量的取值范围选取错误的是（ ）

A．y=2x2中，x取全体实数 B．y=中，x取x≠-1的实数

C．y=中，x取x≥2的实数 D．y=中，x取x≥-3的实数

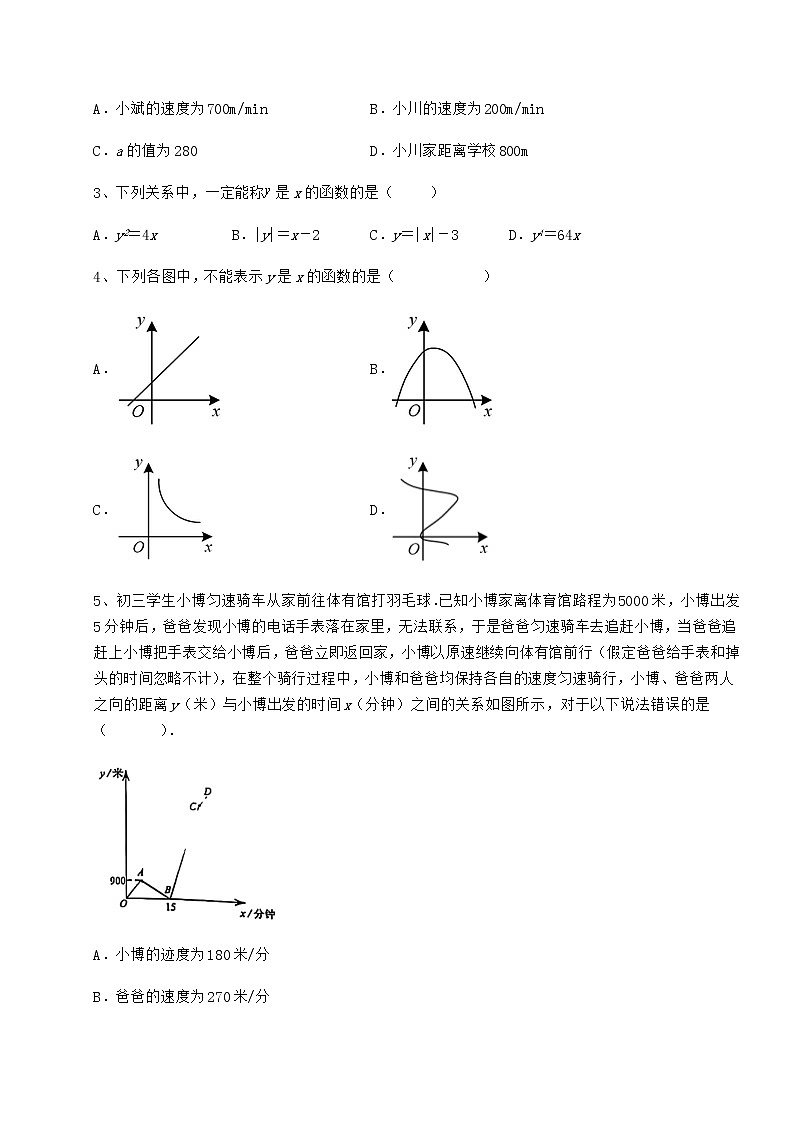
2、小斌家、学校、小川家依次在同一条笔直的街道上，小斌家离学校有2800米，某天，小斌、小川两人分别从自己家中同时出发，相向而行，出发4分钟后，两人在学校相遇，小川继续前行，小斌在学校取好书包后，掉头回家，两人在运动过程中均保持速度不变，两人之间的距离y（米）与小斌出发的时间x（分钟）的关系如图所示（小斌取书包的时间、掉头的时间忽略不计），则下列选项中错误的是（　　）

A．小斌的速度为700m/min B．小川的速度为200m/min

C．a的值为280 D．小川家距离学校800m

3、下列关系中，一定能称是x的函数的是（     ）

A．y2＝4x B．|y|＝x－2 C．y＝|x|－3 D．y4＝64x

4、下列各图中，不能表示y是x的函数的是（            ）

A． B．

C． D．

5、初三学生小博匀速骑车从家前往体有馆打羽毛球．已知小博家离体育馆路程为5000米，小博出发5分钟后，爸爸发现小博的电话手表落在家里，无法联系，于是爸爸匀速骑车去追赶小博，当爸爸追赶上小博把手表交给小博后，爸爸立即返回家，小博以原速继续向体有馆前行（假定爸爸给手表和掉头的时间忽略不计），在整个骑行过程中，小博和爸爸均保持各自的速度匀速骑行，小博、爸爸两人之向的距离y（米）与小博出发的时间x（分钟）之间的关系如图所示，对于以下说法错误的是（       ）．

A．小博的迹度为180米/分

B．爸爸的速度为270米/分

C．点C的坐标是

D．当爸爸出发的时间为分钟或分钟时，爸爸与小博相距800米

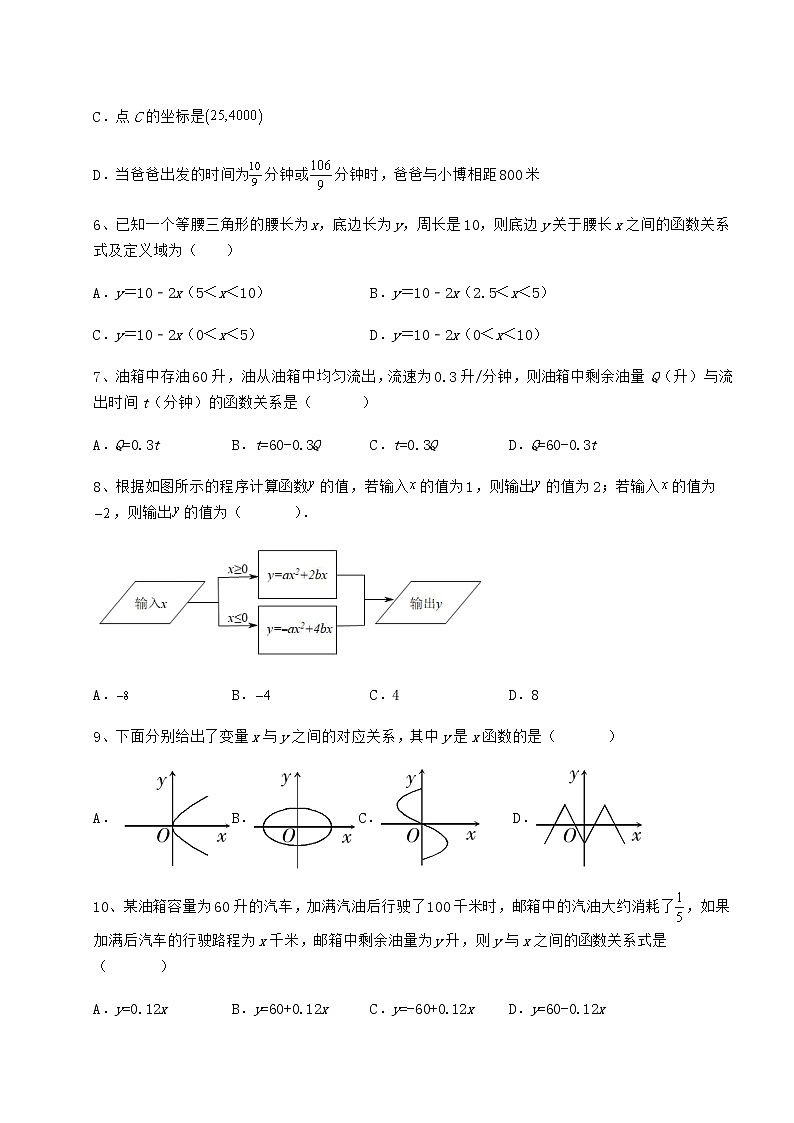
6、已知一个等腰三角形的腰长为x，底边长为y，周长是10，则底边y关于腰长x之间的函数关系式及定义域为（　　）

A．y＝10﹣2x（5＜x＜10） B．y＝10﹣2x（2.5＜x＜5）

C．y＝10﹣2x（0＜x＜5） D．y＝10﹣2x（0＜x＜10）

7、油箱中存油60升，油从油箱中均匀流出，流速为0.3升/分钟，则油箱中剩余油量 Q（升）与流出时间t（分钟）的函数关系是（       ）

A．Q=0.3t B．t=60-0.3Q C．t=0.3Q D．Q=60-0.3t

8、根据如图所示的程序计算函数的值，若输入的值为1，则输出的值为2；若输入的值为，则输出的值为（       ）．

A． B． C．4 D．8

9、下面分别给出了变量x与y之间的对应关系，其中y是x函数的是（       ）

A． B．C．  D．

10、某油箱容量为60升的汽车，加满汽油后行驶了100千米时，邮箱中的汽油大约消耗了，如果加满后汽车的行驶路程为x千米，邮箱中剩余油量为y升，则y与x之间的函数关系式是（       ）

A．y=0.12x B．y=60+0.12x C．y=-60+0.12x D．y=60-0.12x

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、已知三角形底边长为4，高为，三角形的面积为，则与的函数关系式为______．

2、在函数中，自变量的取值范围是______．

3、小亮从学校步行回家，图中的折线反映了小亮离家的距离S（米）与时间t（分钟）的函数关系，根据图象提供的信息，给出以下结论：①他在前12分钟的平均速度是70米/分钟；②他在第19分钟到家；③他在第15分钟离家的距离和第24分钟离家的距离相等；④他在第33分钟离家的距离是720米．其中正确的序号为 ___．

4、小明从家跑步到学校，接着马上原路步行回家．如图是小明离家的路程y（米）与时间t（分）的关系图象，则小明回家的速度是每分钟步行____________米．

5、设路程为s，时间为t，速度为v，当v＝60时，路程和时间的关系式为__________，这个关系式中， __________是常量，__________是变量，__________是__________的函数．

三、解答题（5小题，每小题10分，共计50分）

1、（1）画出函数的图象．

（2）设是x轴上的一个动点，它与x轴上表示的点的距离为y．求y关于x的函数解析式，并画出这个函数的图象．

2、求函数的自变量的取值范围．

3、在一定限度内（所挂物体重量不过）弹簧挂上物体后会伸长，测得一弹簧长度与所挂物体质量有如下关系：

（1）由表格知，弹簧原长为________，所挂物体每增加弹簧伸长________．

（2）请写出弹簧长度与所挂物体质量之间的关系式，并指出自变量取值范围．

（3）预测当所挂物体质量为时，弹簧长度是多少？

（4）当弹簧长度为时，求所挂物体的质量．

4、郑州到西安的路程为480千米，由于西安疫情紧张，郑州物资中心对西安进行支援．甲乙两辆物资车分别从郑州和西安出发匀速行驶相向而行．甲车到西安后立即返回，已知乙车的速度为每小时，且到郑州后停止行驶，进行消毒．它们离各自出发地的距离与行驶时间之间的关系如下图所示．

(1)______，______．

(2)请你求出甲车离出发地郑州的距离与行驶时间之间的函数关系式．

(3)求出点的坐标，并说明此点的实际意义．

(4)直接写出甲车出发多长时间两车相距40千米．

5、一个三角形的底边长为5，高h可以任意伸缩．写出面积S随h变化的解析式，并指出其中的常量与变量，自变量与函数，以及自变量的取值范围．

-参考答案-

一、单选题

1、D

【解析】

【分析】

根据分式的分母不能为0、二次根式的被开方数的非负性即可得．

【详解】

解：A、中，取全体实数，此项正确；

B、，即，

中，取的实数，此项正确；

C、，

，

中，取的实数，此项正确；

D、，且，

，

中，取的实数，此项错误；

故选：D．

【点睛】

本题考查了函数自变量、分式和二次根式，熟练掌握分式和二次根式有意义的条件是解题关键．

2、C

【解析】

【分析】

根据路程÷时间求速度可判断A、B；利用小川继续行走的时间×小川的速度求出a的值，可判断C；利用开始 小斌与小川的距离-小斌到学校的距离可判断D．

【详解】

解：∵小斌家离学校有2800米，出发4分钟后到学校，

∴v小斌=，故选项A正确；

∵小川家离学校有3600-2800=800米，出发4分钟后到学校，

∴v小川=，故选项B正确；

小川继续前行，小斌在学校取好书包后，4分钟后掉头回家，

小川行走的路程为：200m/min×（8-4）=800m，

∴a的值为800m，故选项C不正确；

∵小川家离学校有3600-2800=800米，故选项D正确．

故选C．

【点睛】

本题考查行程问题函数图像信息获取与处理，理解图像横纵轴的意义，折点的含义，终点位置的意义，掌握函数图像信息获取与处理的方法，理解图像横纵轴的意义，折点的含义，终点位置的意义是解题关键．

3、C

【解析】

【分析】

根据函数的定义可知，满足对于x的每一个取值，y都有唯一确定的值与之对应关系，据此即可确定函数．

【详解】

解：根据函数概念可得：在一个变化过程中有两个变量x与y，对于x的每一个确定的值，y都有唯一的值与其对应可得C中y是x的函数，

故选：C．

【点睛】

此题主要考查了函数的概念，关键是掌握函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．

4、D

【解析】

【分析】

根据函数的定义可知，满足对于x的每一个取值，y都有唯一确定的值与之对应关系，即可求解．

【详解】

解：A、对每一个x的值，都有唯一确定的y值与之对应，能表示y是x的函数，故本选项符合题意；

B、对每一个x的值，都有唯一确定的y值与之对应，能表示y是x的函数，故本选项符合题意；

C、对每一个x的值，都有唯一确定的y值与之对应，能表示y是x的函数，故本选项符合题意；

D、对于x的每一个取值，y有时有两个确定的值与之对应，所以y不是x的函数，故本选项不符合题意；

故选：D

【点睛】

本题主要考查了函数的定义，熟练掌握在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量是解题的关键．

5、C

【解析】

【分析】

根据小博出发5分钟后行驶900米，得出小博的迹度为=180米/分,可判断A；爸爸匀速骑车去追赶小博，15分钟时追上小博，设爸爸匀速骑车速度为x米/分，根据两者行驶路程相等列方程15×180=10x，得出x=270米/分，可判断B；点C表示爸爸返回家中两者间的距离，爸爸追上小博用10分钟，（假定爸爸给手表和掉头的时间忽略不计），返回时仍然用10分钟到家，此时小博行驶15+10=25分钟，行驶距离为25×180=4500米，可判断C；设爸爸出发时间为t分钟时，两者之间距离为800米，根据追及与相背而行问题列方程(5+t)180-270t=800或(180+270)×（t-10）=800，解方程可判断D．

【详解】

解：∵小博出发5分钟后行驶900米，

∴小博的迹度为=180米/分,

故选项A正确；      

爸爸匀速骑车去追赶小博，15分钟时追上小博，

设爸爸匀速骑车速度为x米/分，

15×180=10x，

解得：x=270米/分，

∴故选项B正确；

点C表示爸爸返回家中两者间的距离，

爸爸追上小博用10分钟，（假定爸爸给手表和掉头的时间忽略不计），返回时仍然用10分钟到家，此时小博行驶15+10=25分钟，

行驶距离为25×180=4500米，

∴点C（25,4500），

故选项C不正确，

设爸爸出发时间为t分钟时，两者之间距离为800米，

(5+t)180-270t=800或(180+270)×（t-10）=800，

解得：分钟或分钟，

当爸爸出发的时间为分钟或分钟时，爸爸与小博相距800米，

故选项D正确．

故选C．

【点睛】

本题考查从函数图像获取信息和处理，掌握从函数图像获取信息和处理，关键掌握图像中的横纵轴于折叠表示的意义．

6、B

【解析】

【分析】

根据等腰三角形的定义即三角形的周长公式列出底边y关于腰长x之间的函数关系式，根据三角形的三边关系以及底边大于0，列出不等式组，进而求得定义域．

【详解】

一个等腰三角形的腰长为x，底边长为y，周长是10，

即

即

解得

即

解得

底边y关于腰长x之间的函数关系式为

故选B

【点睛】

本题考查了等腰三角形的定义，三角形的三边关系，函数解析式，掌握以上知识是解题的关键．

7、D

【解析】

【分析】

根据油箱中剩余油量=总存油量-流出的油量，列出函数关系式即可．

【详解】

解：根据题意：

油箱中剩余油量 Q（升）与流出时间t（分钟）的函数关系是：，

故选：D．

【点睛】

本题考查了列函数解析式，关键是正确理解题意，找出题目中的等量关系．

8、A

【解析】

【分析】

输入，则有；输入，则有，将代数式的值代入求解即可．

【详解】

解：输入，则有；

输入，则有；

故选A．

【点睛】

本题考查了程序流程图与代数式求值．解题的关键在于正确求解代数式的值．

9、D

【解析】

【分析】

函数的意义反映在图象上简单的判断方法是：做垂直轴的直线在左右平移的过程中与函数图象只会有一个交点．

【详解】

解：根据函数的意义可知：对于自变量的任何值，都有唯一的值与之相对应，所以D正确．

故选：D．

【点睛】

本题主要考查了函数图象的读图能力，解题的关键是要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．

10、D

【解析】

【分析】

先求出1千米的耗油量，再求行驶x千米的耗油量，最后求油箱中剩余的油量即可．

【详解】

解：∵每千米的耗油量为：60×÷100=0.12（升/千米），

∴y=60-0.12x，

故选：D．

【点睛】

本题考查了函数关系式，求出1千米的耗油量是解题的关键．

二、填空题

1、

【解析】

【分析】

根据三角形面积公式可得结果．

【详解】

解：由题意，

故答案为：．

【点睛】

本题考查了三角形的面积公式，根据题意，找到所求量的等量关系是解决问题的关键．

2、全体实数

【解析】

【分析】

根据整式函数的自变量不受限制即可求解

【详解】

解：∵函数是整式函数，自变量不受限制，

∴自变量x的取值范围是全体实数．

故答案为全体实数．

【点睛】

本题考查函数自变量的取值范围，掌握整式函数不受限制，分式函数要求分母不为0，根式函数要求被开方式有意义，零指数函数要求底数不为0是解题关键．

3、①④

【解析】

【分析】

由图象可以直接得出前12分钟小亮的平均速度，从而得出①正确；由图象可知从12分到19分小亮又返回学校，可以判断②错误；分别求出小亮第15分和第24分离家距离可以判断③错误；求出小亮33分离家距离，可以判断④正确．

【详解】

解：由图象知，前12分中的平均速度为：（1800−960）÷12＝70（米/分），

故①正确；

由图象知，小亮第19分中又返回学校，

故②错误；

小亮在返回学校时的速度为：（1800−960）÷（19−12）＝840÷7＝120（米/分），

∴第15分离家距离：960＋（15−12）×120＝1320，

从21分到41分小亮的速度为：1800÷（41−21）＝1800÷20＝90（米/分），

∴第24分离家距离：1800−（24−21）×90＝1800−270＝1530（米），

∵1320≠1530，

故③错误；

小亮在33分离家距离：1800−（33−21）×90＝1800−1080＝720（米），

故④正确，

故答案为：①④．

【点睛】

本题考查函数图像，关键是利用已知信息和图象所给的数据分析题意，依次解答．

4、50

【解析】

【分析】

根据总路程÷回家用的时间即可求解．

【详解】

解：小明回家用了15-5=10分钟，

总路程为500，

故小明回家的速度为：500÷10=50（米/分），

故答案为50．

【点睛】

本题考查由图象理解对应函数关系及其实际意义，应把所有可能出现的情况考虑清楚．

5、     s=60t     60     t和s     s     t

【解析】

略

三、解答题

1、（1）见解析；（2），见解析

【解析】

【分析】

（1）先列表，然后画出函数图像即可；

（2）先根据题意求出函数解析式，然后列表，最后画出函数图像即可

【详解】

解：（1）由题意得：y=|x-1|，即y；

函数图象如图：

（2）由题意得：y=|x-（-3）|=|x+3|，即y；

函数图象如图：

【点睛】

本题主要考查函数及其图像，掌握函数图象的画法是解题的关键．

2、或.

【解析】

【分析】

根据二次根式的性质和分式的意义，被开方数大于等于0且分母不为0，即可得出自变量的取值范围．

【详解】

解：要使函数有意义，

则， 即①或②，

解不等式组①得，

解不等式组②得

∴自变量取值是或．

【点睛】

本题考查函数自变量的取值范围，当函数表达式是分式时，必须满足分母不为0，若函数表达式中有二次根式，则也要满足被开方数大于等于0．

3、（1）12，0.5；（2），；（3）；（4）

【解析】

【分析】

（1）由表格可得弹簧原长以及所挂物体每增加弹簧伸长的长度；

（2）由（1）中的结论可求出弹簧长度与所挂物体质量之间的函数关系式；

（3）令，求出y的值即可；

（4）令，求出x的值即可．

【详解】

解：（1）由表格可知，所挂物体质量时，弹簧长度为，

∴弹簧原长为，

∵，

∴所挂物体每增加弹簧伸长；

（2）由（1）可知：弹簧长度与所挂物体质量之间的函数关系式为，

∵所挂物体质量不过，

∴自变量x的取值范围是；

（3）将代入，得，

∴当所挂物体质量为时，弹簧长度是；

（4）将代入，得，

解得：，

∴当弹簧长度为时，物体质量是．

【点睛】

本题考查了函数的关系式及函数值，解题的关键是根据图表信息解决问题．

4、 (1)8，6.5

(2)

(3)点P的坐标为（5，360），点P的实际意义是：甲车在行驶5小时后，甲乙两车分别距自己的出发地的距离为360千米

(4)当甲车出发2.4小时或2.8小时或小时两车相距40千米

【解析】

【分析】

（1）先根据题意判断出直线的函数图像时乙车的，折线的函数图像时甲车的，然后求出甲车的速度即可求出甲返回郑州的时间，即可求出m；然后算出乙车从西安到郑州需要的时间即可求出n；

（2）分甲从郑州到西安和从西安到郑州两种情况求解即可；

（3）根据函数图像可知P点代表的实际意义是：在P点时，甲乙两车距自己的出发地的距离相同，由此列出方程求解即可；

（4）分情况：当甲车在去西安的途中，甲乙两车相遇前，当甲车在去西安的途中，甲乙两车相遇后，当甲车在返回郑州的途中，乙未到郑州时，当甲车在返回郑州的途中，乙已经到郑州时，四种情况讨论求解即可．

(1)

解：∵甲乙两辆物资车分别从郑州和西安出发匀速行驶相向而行．甲车到西安后立即返回，乙车到底郑州后立即停止，

∴直线的函数图像是乙车的，折线的函数图像是甲车的，

由函数图像可知，甲车4小时从郑州行驶到西安走了480千米，

∴甲车的速度=480÷4=120千米/小时，

∴甲车从西安返回郑州需要的时间=480÷120=4小时，

∴m=4+4=8；

∵乙车的速度为80千米/小时，

∴乙车从西安到达郑州需要的时间=480÷80=6小时，

∵由函数图像可知乙车是在甲车出发0.5小时后出发，

∴n=0.5+6=6.5，

故答案为：8，6.5；

(2)

解：当甲车从郑州去西安时，

∵甲车的速度为120千米/小时，

∴甲车与郑州的距离，

当甲车从西安返回郑州时，

∵甲车的速度为120千米/小时，

∴甲车与郑州的距离，

∴；

(3)

解：根据函数图像可知P点代表的实际意义是：在P点时，甲乙两车距自己的出发地的距离相同，

∵此时甲车处在返程途中，

∴，

解得，

∴，

∴点P的坐标为（5，360），

∴点P的实际意义是：甲车在行驶5小时后，甲乙两车分别距自己的出发地的距离为360千米；

(4)

解：当甲车在去西安的途中，甲乙两车相遇前，

由题意得：，

解得；

当甲车在去西安的途中，甲乙两车相遇后，

由题意得：，

解得；

当甲车在返回郑州的途中，乙未到郑州时，

由题意得：

解得（不符合题意，舍去），

当甲车在返回郑州的途中，乙已经到郑州时，

由题意得：

解得；

综上所述，当甲车出发2.4小时或2.8小时或小时两车相距40千米．

【点睛】

本题主要考查了从函数图像获取信息，一元一次方程的应用，正确理解题意是解题的关键．

5、常量，变量h，S，自变量，函数S，．

【解析】

【分析】

根据三角形的面积公式，可得函数关系式．

【详解】

解：由三角形的面积公式，得：，

常量是，变量h，S，自变量，函数S．

【点睛】

本题考查了函数关系式，利用三角形的面积公式得出函数解析式是解题关键．