2022届高三数学二轮复习课件：专题四　专项突破四　立体几何解答题

这是一份2022届高三数学二轮复习课件：专题四　专项突破四　立体几何解答题，共60页。PPT课件主要包含了必备知识•精要梳理，关键能力•学案突破，精典对练·得高分等内容，欢迎下载使用。
1.证明线线平行和线线垂直的常用方法(1)证明线线平行:①利用平行线的传递性;②利用平行四边形进行平行转换;③利用三角形的中位线定理;④利用线面平行、面面平行的性质定理等.(2)证明线线垂直:①利用等腰三角形三线合一的性质;②利用勾股定理;③利用线面垂直的性质等.
2.证明线面平行和线面垂直的常用方法(1)证明线面平行:①利用线面平行的判定定理;②利用面面平行的性质.(2)证明线面垂直:①利用线面垂直的判定定理;②利用面面垂直的性质定理.3.证明面面平行和面面垂直的常用方法(1)证明面面平行最常用的方法是利用面面平行的判定定理.(2)证明面面垂直最常用的方法是利用面面垂直的判定定理.
4.利用空间向量证明平行与垂直设直线l的方向向量为a=(a1,b1,c1),平面α,β的法向量分别为μ=(a2,b2,c2),v=(a3,b3,c3),l⊄α,则(1)线面平行:l∥α⇔a⊥μ⇔a·μ=0⇔a1a2+b1b2+c1c2=0.(2)线面垂直:l⊥α⇔a∥μ⇔a=kμ⇔a1=ka2,b1=kb2,c1=kc2(k≠0).(3)面面平行:α∥β⇔μ∥v⇔μ=λv⇔a2=λa3,b2=λb3,c2=λc3(λ≠0).(4)面面垂直:α⊥β⇔μ⊥v⇔μ·v=0⇔a2a3+b2b3+c2c3=0.
5.利用空间向量求空间角(1)两条异面直线所成的角:设异面直线l,m的方向向量分别为a,b,且它们所
考向一　空间位置关系的证明
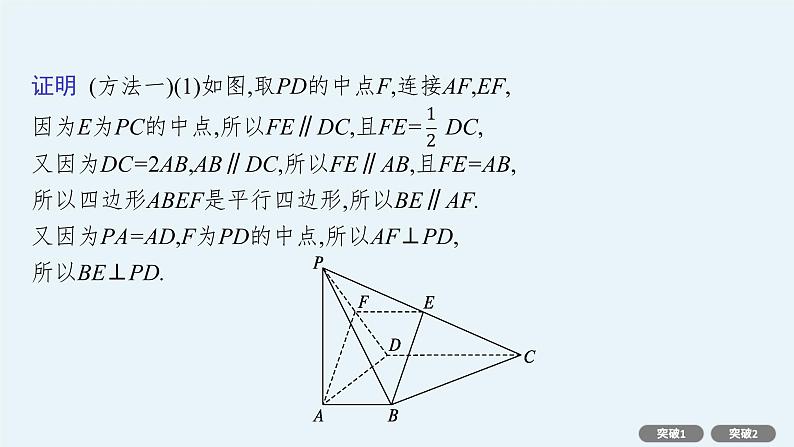
[例1](2021·江苏宿迁期末)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=PA=2,AB=1,E为PC的中点.求证:(1)BE⊥PD;(2)BE∥平面PAD;(3)平面PCD⊥平面PAD.
证明 (方法一)(1)如图,取PD的中点F,连接AF,EF,因为E为PC的中点,所以FE∥DC,且FE= DC,又因为DC=2AB,AB∥DC,所以FE∥AB,且FE=AB,所以四边形ABEF是平行四边形,所以BE∥AF.又因为PA=AD,F为PD的中点,所以AF⊥PD,所以BE⊥PD.
(2)由(1)知BE∥AF,AF⊂平面PAD,BE⊄平面PAD,所以BE∥平面PAD.(3)因为PA⊥底面ABCD,所以PA⊥AB.又因为AD⊥AB,PA∩AD=A,所以AB⊥平面PAD.又因为AB∥DC,所以DC⊥平面PAD.又因为DC⊂平面PCD,所以平面PCD⊥平面PAD.
(方法二)因为PA⊥底面ABCD,AD⊥AB,所以PA,AB,AD两两互相垂直.以点A为坐标原点,AB,AD,AP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系如图所示.
(3)由(2)知 为平面PAD的一个法向量,则DC⊥平面PAD.又DC⊂平面PCD,所以平面PCD⊥平面PAD.
方法总结证明空间中位置关系的方法证明空间中的平行、垂直关系,均可利用两种方法:一是几何法,二是向量法.在实际应用中,可灵活处理,如果题目给出的空间图形适合建立空间直角坐标系,那么可建系后利用坐标运算来证明位置关系.
(2021·浙江金华期中)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC= AB,B1C1∥BC,且B1C1= BC,二面角A1-AB-C是直二面角.求证:(1)A1B1⊥平面AA1C;(2)AB1∥平面A1C1C.
证明 (方法一)(1)因为AB=AC,BC= AB,所以AB2+AC2=BC2,所以AB⊥AC.因为四边形A1ABB1是正方形,所以A1B1∥AB,AB⊥AA1.又AA1∩AC=A,所以AB⊥平面AA1C.所以A1B1⊥平面AA1C.
(2)如图,取BC的中点D,连接AD,B1D,C1D.因为B1C1∥BC,且B1C1= BC=BD,所以四边形BDC1B1是平行四边形,所以C1D∥BB1,且C1D=BB1.因为四边形A1ABB1是正方形,所以AA1∥BB1,且AA1=BB1.所以C1D∥AA1,且C1D=AA1,
所以四边形AA1C1D是平行四边形,
所以A1C1∥AD.又AD⊄平面A1C1C,A1C1⊂平面A1C1C,所以AD∥平面A1C1C.同理B1D∥平面A1C1C,又B1D∩AD=D,所以平面B1AD∥平面A1C1C.又AB1⊂平面B1AD,所以AB1∥平面A1C1C.(方法二)因为二面角A1-AB-C是直二面角,四边形A1ABB1为正方形,所以AA1⊥平面BAC.又因为AB=AC,BC= AB,所以∠CAB=90°,即AC⊥AB.所以AB,AC,AA1两两互相垂直.如图,建立空间直角坐标系,设AB=2,则A(0,0,0),B1(0,2,2),A1(0,0,2),C(2,0,0),C1(1,1,2).
考向二　利用空间向量求线面角命题角度1　求线面角
[例2-1](2021·广东深圳高三二模)如图,在直四棱柱ABCD-A1B1C1D1中,AB∥CD,DC=2,AA1=3,AB=BC=AD=1,点E,F分别在侧棱AA1,CC1上,且A1E=CF=1.(1)求证:BC∥平面D1EF;(2)求直线AD与平面D1EF所成角的正弦值.
(1)证明 分别取D1F,CD的中点N,M,连接AM,MN,EN,如图所示,因为M,N分别为CD,D1F的中点,则MN为梯形CFD1D的中位线,所以MN∥CC1∥DD1,且有MN= (CF+DD1)=2,因为A1E=1,AA1∥DD1,所以AE=2=MN,且AE∥MN,所以四边形AENM为平行四边形,故EN∥AM.因为M为CD的中点,则CM= CD=AB,因为AB∥CD,则CM∥AB,所以四边形ABCM为平行四边形,则AM∥BC,故BC∥EN.又BC⊄平面D1EF,EN⊂平面D1EF,因此BC∥平面D1EF.
名师点析利用向量求直线与平面所成角的方法(1)分别求出直线与它在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角).(2)求出直线的方向向量m,平面的法向量n,设直线与平面所成的角为θ,则sin θ=|cs|= ,求出θ的值.
精典对练·得高分(2021·湖南师大附中高三月考)如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F分别是PC,PB的中点.(1)求证:BC⊥平面PAC;(2)记平面AEF与平面ABC的交线为直线l,点Q为直线l上动点,求直线PQ与平面AEF所成角的取值范围.
(1)证明 ∵C是以AB为直径的圆O上异于A,B的点,∴BC⊥AC.又平面PAC∩平面ABC=AC,平面PAC⊥平面ABC,BC⊂平面ABC,∴BC⊥平面PAC.(2)解 由已知,BC∥EF,又EF⊂平面EFA,BC⊄平面EFA,∴BC∥平面EFA,又BC⊂平面ABC,平面EFA∩平面ABC=l,∴BC∥l.以C为坐标原点,CA,CB所在直线分别为x轴、y轴,过C且垂直于平面ABC的直线为z轴,建立空间直角坐标系.
数学思想·扩思路转化与化归思想(2021·山东省实验中学一模)如图,在长方体ABCD-A1B1C1D1中,AB=1,BC=2,CC1=2,E,F分别为BC,CC1的中点.(1)求过E,F,D1三点的截面的面积;(2)一只小虫从点A经BB1上一点P到达点C1,求小虫所经过的路程最短时,直线ED1与平面APC1所成角的正弦值.
(2)以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系如图所示,则A(2,0,0),C1(0,1,2),D1(0,0,2),E(1,1,0).
名师点析沿几何体表面距离之和最小问题,通常采取化曲为直的思想方法,将几何体的表面展开,在平面内,将折线转化为直线,进而求解出距离之和最小等问题.
命题角度2　已知线面角求线段长
又因为AB⊥B1D,AB∩CD=D,所以B1D⊥平面ABC.又因为B1D⊂平面ABB1A1,所以平面ABB1A1⊥平面ABC.
方法点拨已知线面角求其他量的解法要点(1)正确设置变量:已知线面角确定点的位置或线段长度时,可以直接在空间直角坐标系中设出相关点的坐标(只有一个坐标未知),也可以利用共线向量的设法,例如点P在线段AB上,可设 (0≤λ≤1),这样可将点P的坐标用一个变量λ表示.
(2)准确进行转化:已知直线的方向向量为m,平面的法向量为n.
精典对练·得高分(2021·广东汕头一模)如图,在圆柱OO1中,四边形ABCD是其轴截面,EF为☉O1的直径,且EF⊥CD,AB=2,BC=a(a>1).(1)求证:BE=BF;
(2)若直线AE与平面BEF所成角的正弦值为 ,求二面角A-BE-F的余弦值.
(1)证明 如图,连接BO1,依题意,在圆柱OO1中,BC⊥平面CEDF,∵EF⊂平面CEDF,∴EF⊥BC.又EF⊥CD,BC∩CD=C,∴EF⊥平面ABCD.又BO1⊂平面ABCD,∴EF⊥BO1.又O1为EF的中点,∴BE=BF.
考向三　利用空间向量求二面角命题角度1　求二面角
[例3-1](2021·湖南长沙模拟)如图,在四棱锥P-ABCD中,AB∥CD,∠ABC=90°,AB=1,BC= ,△PDC是边长为2的等边三角形,平面PDC⊥平面ABCD,E为PC的中点.(1)设平面PAD∩平面PBC=l,求证:DE⊥l;(2)求平面PAD与平面PBC所成锐二面角的余弦值.
解 (1)因为AB∥CD,∠ABC=90°,所以BC⊥CD.又平面PDC⊥平面ABCD,平面PDC∩平面ABCD=DC,BC⊂平面ABCD,所以BC⊥平面PDC.又BC⊂平面PBC,所以平面PDC⊥平面PBC.因为△PDC为等边三角形,E为PC的中点,所以DE⊥PC.又平面PDC∩平面PBC=PC,DE⊂平面PDC,所以DE⊥平面PBC.又l⊂平面PBC,所以DE⊥l.
(2)设DC的中点为O,因为PD=PC,所以PO⊥DC.因为平面PDC⊥平面ABCD,平面PDC∩平面ABCD=DC,PO⊂平面PDC,所以PO⊥平面ABCD.因为AB=1,CD=2,O为CD的中点,所以AB=OC.又AB∥CD,所以AB∥OC.又∠ABC=90°,所以四边形ABCO为矩形,所以OA⊥OC.
名师点析利用空间向量求二面角的步骤(1)分别求出两个半平面的一个法向量;(2)求出两个法向量的夹角;(3)根据图形判断二面角的平面角是锐角还是钝角,利用二面角的平面角与两个法向量的夹角的关系,求出二面角.
精典对练·得高分(2021·广东阳江高三模拟)如图,在四棱锥A-BCDE中,BC∥DE,BE⊥BC,AB=BC=AC=2DE=2BE.(1)证明:AD⊥BC;(2)若平面BCDE⊥平面ABC,经过点A,D的平面α将四棱锥A-BCDE分成左、右两部分的体积之比为1∶2,求平面α与平面ADC所成锐二面角的余弦值.
(1)证明 如图,取BC的中点O,连接AO,DO,因为BC∥DE,BC=2DE,O是BC的中点,BE⊥BC,所以BO∥DE,BO=DE,BE⊥BO,四边形BODE是矩形,BC⊥DO,因为AB=BC=AC,所以△ABC是等边三角形,BC⊥AO.又因为AO∩DO=O,所以BC⊥平面ADO.因为AD⊂平面AOD,所以AD⊥BC.
(2)解 因为平面BCDE⊥平面ABC,平面BCDE∩平面ABC=BC,DO⊥BC,所以DO⊥平面ABC.因为S△CDO∶S矩形DOBE=1∶2,所以VA-CDO∶VA-DOBE=1∶2,所以平面ADO即平面α.
命题角度2　已知二面角求其他量[例3-2](2021·新高考 Ⅰ,20)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)证明:AO⊥CD;(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.
(1)证明 在△ABD中,∵AB=AD,O为BD的中点,∴AO⊥BD.∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊂平面ABD,∴AO⊥平面BCD.∵CD⊂平面BCD,∴AO⊥CD.
(2)解 (方法一)如图,过点E作EN∥AO交BD于N,过点N作NM∥CD交BC于M.∵AO⊥平面BCD,EN∥AO,∴EN⊥平面BCD.∴EN⊥BC.在△BCD中,∵OB=OD=OC=1,∴∠BCD=90°,即DC⊥BC.∵NM∥CD,∴NM⊥BC.又EN∩NM=N,∴BC⊥平面EMN,∴BC⊥ME.∴二面角E-BC-D的平面角是∠EMN=45°,
设平面EBC的法向量为n=(x,y,z),则
名师点析已知二面角求其他量的解法要点(1)正确设置变量,已知二面角求其他量时,关键是在空间直角坐标系中设出相关点的坐标或相关向量的坐标,从而用设出的参数表示出两个平面的法向量.(2)准确建立方程,根据已知条件(二面角的度数、二面角的余弦值、二面角的正弦值等)建立关于参数的方程.(3)求解方程,得到参数值,注意根据二面角的大小对参数值进行取舍,进而得到其他量.
精典对练·得高分(2021·广东梅州二模)如图,在四棱锥B-ACDE中,平面ABC⊥平面ACDE,△ABC是等边三角形,在直角梯形ACDE中,AE∥CD,AE⊥AC,AE=1,AC=CD=2,P是棱BD的中点.(1)求证:EP⊥平面BCD;(2)设点M在线段AC上,若平面PEM与平面EAB所成的锐二面角的余弦值为
(1)证明 如图,取BC的中点O,连接PO,AO.因为△ABC为等边三角形,所以AO⊥BC.因为平面ABC⊥平面ACDE,AE⊥AC,平面ABC∩平面ACDE=AC,AE⊂平面ACDE,所以AE⊥平面ABC.又AO⊂平面ABC,所以AE⊥AO.又AE∥CD,所以CD⊥AO.又CD∩BC=C,所以AO⊥平面BCD.因为P为BD的中点,O为BC的中点,
所以PO= CD=1,PO∥CD.又AE∥CD,AE=1,所以AE∥PO,AE=PO,所以四边形AEPO为平行四边形,所以EP∥AO,所以EP⊥平面BCD.
(2)解 由(1)知PO∥AE,AE⊥平面ABC,AO⊥BC,所以PO⊥平面ABC,所以OA,OB,OP两两互相垂直.
易错防范·不丢分(2021·山东滨州二模)如图,在四棱锥P-ABCD中,O是BD的中点,PO⊥平面
(1)证明 如图,设AC∩BD=N,连接PN,OA,OC.因为∠DAB=∠BCD=90°,O为BD的中点,所以OA=OD=OC,即O为△ACD的外心.又AD=AC=CD,所以△ACD为等边三角形,所以O为△ACD的中心.所以AC⊥BD.由PO⊥平面ABCD,可得PO⊥AC.
又PO∩BD=O,所以AC⊥平面PDB,所以AC⊥DP.
所以DP2+PN2=DN2,所以DP⊥PN.又PN∩AC=N,所以DP⊥平面APC.又DP⊂平面ADP,所以平面ADP⊥平面APC.
易错警示由于二面角的大小与两个面的法向量的夹角并不完全相等,因此要注意结合图形判断二面角的范围来确定参数的取值,忽视对范围的判断将会导致错误.
考向一　立体几何中的翻折问题
(1)求证:平面BC1E⊥平面ABED;(2)求直线BC1与平面AC1D所成角的正弦值.
(1)证明 连接AE,由已知得AE=2.∵CE∥AB,CE=AB=AE=2,∴四边形ABCE为菱形.连接AC交BE于点F,则CF⊥BE.
∴C1F⊥AF.又BE∩AF=F,∴C1F⊥平面ABED.又C1F⊂平面BC1E,所以平面BC1E⊥平面ABED.
名师点析立体几何中翻折问题的求解策略(1)解决翻折问题最关键的就是对比翻折前后的图形,找到哪些点、线、面的位置关系和数量关系没有发生变化,哪些发生了变化,这些不变的量和变化的量反映了翻折后空间图形的结构特征,在证明和求解的过程中应恰当地加以利用.(2)一般地,位于折痕同侧的点、线、面的位置关系和数量关系不发生变化,而位于折痕两侧的点、线、面的位置关系和数量关系会发生变化.特别地,与折痕垂直的线段,翻折前后垂直关系不变(常用于找翻折后形成的二面角的平面角);与折痕平行的线段,翻折后平行关系保持不变.
精典对练·得高分(2021·山东济南二模)如图①,在等腰梯形ABCD中,E为CD的中点,AB=BC=CE,将△ADE,△BCE分别沿AE,BE折起,使得平面ADE⊥平面ABE,平面BCE⊥平面ABE,如图②.
(1)求证:AB∥CD;(2)设平面ADE与平面BCE的交线为l,求二面角D-l-C的大小.
(1)证明 由题意可知△ADE,△ABE,△BCE为全等的等边三角形.如图,分别过点C,D作CM⊥BE,DN⊥AE,垂足分别为M,N,连接MN,则M,N分别为BE,AE的中点,CM=DN.∵平面BCE⊥平面ABE,平面BCE∩平面ABE=BE,CM⊂平面BCE,∴CM⊥平面ABE.同理DN⊥平面ABE,∴CM∥DN.
∴四边形CDNM为平行四边形,∴CD∥MN.又M,N分别为BE,AE的中点,∴MN∥AB,∴AB∥CD.
(2)解 连接BN,则BN⊥AE.由(1)知DN⊥平面ABE,则NA,NB,ND两两互相垂直.以N为坐标原点,NA,NB,ND所在直线分别为x轴、y轴、z轴,建立空间直角坐标系如图所示.
易错防范·不丢分(2021·广东佛山二模)如图①,在梯形ABCD中,AB∥CD,∠BAD=90°,AD=CD= AB,E为AB的中点,沿DE将△ADE折起,使点A到达点P的位置,如图②所示.
(1)求证:DE⊥PC;(2)若PC=PD,求平面PBE与平面PCD所成二面角的正弦值.
(1)证明 如图,取DE的中点O,连接OP,OC,CE.在梯形ABCD中,因为∠BAD=90°,AD=CD= AB,AB∥CD,E为AB的中点,所以四边形AECD为正方形,AE=AD=CE=CD.由翻折可知PE=PD=CE=CD.又O为DE的中点,所以OP⊥DE,OC⊥DE.又OP∩OC=O,所以DE⊥平面OPC.又PC⊂平面OPC,所以DE⊥PC.
(2)解 不妨设CD=2,则PD=2,OP=OC=又PC=PD=2,所以OP2+OC2=PC2,所以OP⊥OC.结合(1)可知OP,OC,OD两两互相垂直.以O为原点,OC,OD,OP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系如图所示.
易错警示翻折问题中容易出现的错误是对翻折后的空间图形分析不到位,不能根据翻折前平面图形中的位置关系与数量关系推出翻折后空间图形的位置关系与数量关系,从而找不到解题的突破口,所以应注意分析翻折前后图形间的联系,找到有用信息解决问题.
考向二　立体几何中的探索性问题[例2](2021·河北石家庄二模)如图,在四棱锥P-ABCD中,底面ABCD为正方形,△PAB为等边三角形,平面PAB⊥平面ABCD,E为AD的中点.(1)求证:CE⊥PD;(2)在线段BD(不包括端点)上是否存在点F,使直线AP与平面PEF所成角的正弦值为 ?若存在,确定点F的位置;若不存在,请说明理由.
解 取AB的中点O,连接PO,因为△PAB为等边三角形,所以PO⊥AB.又平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,PO⊂平面PAB,所以PO⊥平面ABCD.取CD的中点G,连接OG,则OB,OP,OG两两互相垂直.
以O为原点,OB,OG,OP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系如图所示.
设AB=2,则C(1,2,0),P(0,0, ),E(-1,1,0),D(-1,2,0),A(-1,0,0),B(1,0,0).
名师点析立体几何中探索性问题的求解策略(1)探索性问题的一般解法是:①可先猜后证,即先观察与尝试给出条件再证明.②首先假设结论成立,然后把这个假设作为已知条件,与题目的其他已知条件一起进行推理论证和计算.在推理论证和计算无误的前提下,若得到一个合理的结论,则说明假设成立;若得到一个不合理的结论,则说明假设不成立.(2)涉及在线段上是否存在符合某条件的点的问题,可以先根据条件猜测点的位置,特别注意特殊位置关系和极端情形的应用.(3)可借助空间直角坐标系将动点用坐标(含参数)表示出来,然后根据已知条件建立关于参数的方程(组),由此解决探索性问题.
精典对练·得高分(2021·广东茂名二模)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为矩形,AD=2,AB=1,PA= ,E为线段BC上一动点.(1)若F为线段PD上一点,PD=3DF,是否存在点E,使得EF∥平面PAB?若存在,求出CE的长,若不存在,请说明理由.(2)若DE⊥PE,求直线PC与平面PED所成角的余弦值.
解 依题意,以A为原点,AB,AD,AP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系如图所示.
易错防范·不丢分(2021·湖南娄底高三模拟)如图①,在△ABC中,AC=BC,AC⊥BC,D为AB的中点.沿CD将△ACD折起,折起后的A点记为E(如图②).
(1)求证:平面ECD⊥平面EBD.(2)若∠EDA=60°,线段CE上是否存在一点F,使得二面角F-AB-C的余弦值
(1)证明 由已知可得CD⊥BD,CD⊥DE,又DB∩DE=D,∴CD⊥平面EBD,而CD⊂平面ECD,∴平面ECD⊥平面EBD.
(2)解 以D为原点,直线DC,DB分别为x轴、y轴,平面BDE内垂直BD的直线为z轴,建立空间直角坐标系(如图),