数学八年级下册第十七章 方差与频数分布综合与测试复习练习题

京改版八年级数学下册第十七章方差与频数分布定向测试

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、对于一列数据(数据个数不少于6），如果去掉一个最大值和一个最小值，那么这列数据分析一定不受影响的是（　　）

A．平均数 B．中位数 C．众数 D．方差

2、某企业为了解员工给灾区“爱心捐款”的情况，随机抽取部分员工的捐款金额整理绘制成如图所示的直方图，根据图中信息，下列结论错误的是（　　）

A．样本中位数是200元

B．样本容量是20

C．该企业员工捐款金额的极差是450元

D．该企业员工最大捐款金额是500元

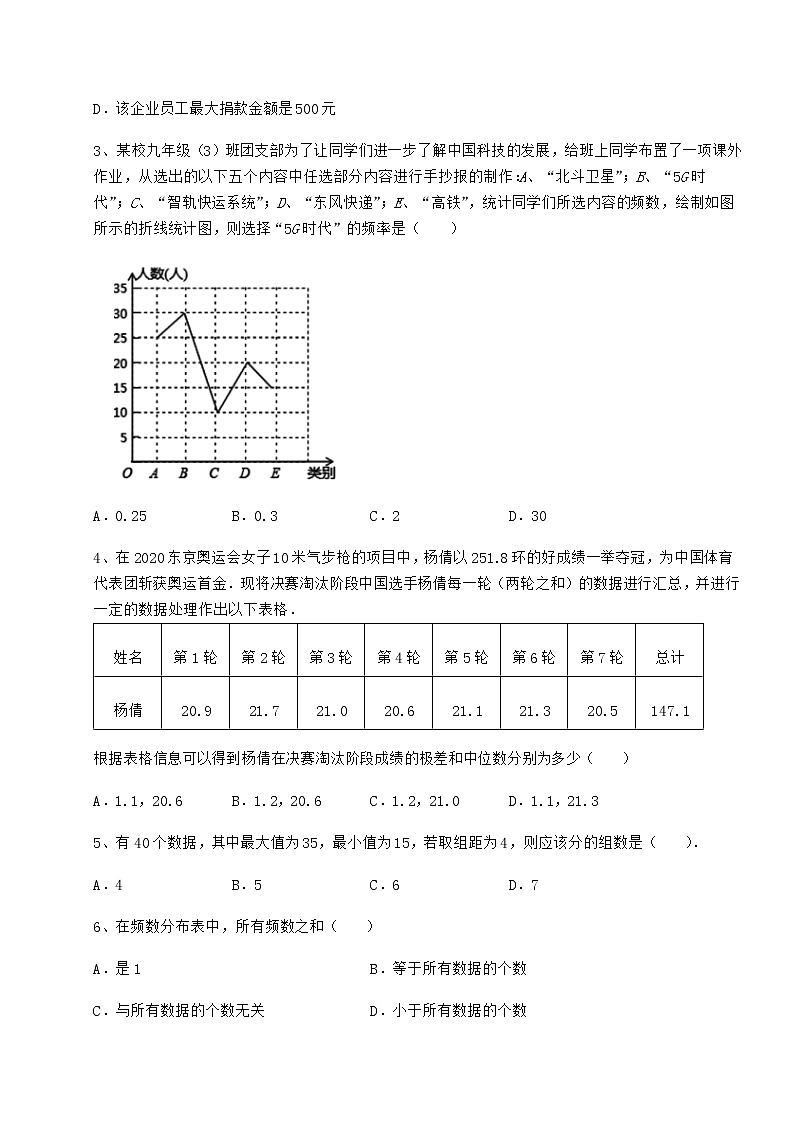
3、某校九年级（3）班团支部为了让同学们进一步了解中国科技的发展，给班上同学布置了一项课外作业，从选出的以下五个内容中任选部分内容进行手抄报的制作：A、“北斗卫星”；B、“5G时代”；C、“智轨快运系统”；D、“东风快递”；E、“高铁”，统计同学们所选内容的频数，绘制如图所示的折线统计图，则选择“5G时代”的频率是（    ）

A．0.25 B．0.3 C．2 D．30

4、在2020东京奥运会女子10米气步枪的项目中，杨倩以251.8环的好成绩一举夺冠，为中国体育代表团斩获奥运首金．现将决赛淘汰阶段中国选手杨倩每一轮（两轮之和）的数据进行汇总，并进行一定的数据处理作出以下表格．

根据表格信息可以得到杨倩在决赛淘汰阶段成绩的极差和中位数分别为多少（    ）

A．1.1，20.6 B．1.2，20.6 C．1.2，21.0 D．1.1，21.3

5、有40个数据，其中最大值为35，最小值为15，若取组距为4，则应该分的组数是（    ）．

A．4 B．5 C．6 D．7

6、在频数分布表中，所有频数之和（    ）

A．是1 B．等于所有数据的个数

C．与所有数据的个数无关 D．小于所有数据的个数

7、在某中学举行的“筑梦路上”演讲比赛中，八年级5名参赛选手的成绩分别为：90，93，89，90，88.关于这5名选手的成绩，下列说法正确的是（    ）

A．平均数是89 B．众数是93

C．中位数是89 D．方差是2.8

8、一组数据a－1、b－1、c－1、d－1、e－1、f－1、g－1的平均数是m，方差是n，则另一组数据2a－3、2b－3、2c－3、2d－3、2e－3、2f－3、2g－3的平均数和方差分别是（    ）

A．2m－3、2n－3 B．2m－1、4n C．2m－3、2n D．2m－3、4n

9、一个有80个样本的数据组中，样本的最大值是145，最小值是50，取组距为10，那么可以分成（    ）组．

A．10 B．9 C．8 D．7

10、甲、乙、丙、丁四位同学五次数学测验成绩统计如表．如果从这四位同学中，选出一位成绩较好且状态稳定的同学参加全国数学联赛，那么应选（    ）

A．甲 B．乙 C．丙 D．丁

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、数据1，3，2，5和x的平均数是3，则这组数据的方差是____________．

2、南京2021年11月1号的最高气温为22℃，最低气温为12℃，该日的气温极差为 __．

3、为了考察某种小麦的长势，从中抽取了10株麦苗，测得苗高（单位：cm）为：16，9，14，11，12，10，16，8，17，19，则这组数据的极差是____．

4、据统计，某车间10名员工每人日平均生产零件个数为6，方差为2.5，引入新技术后，每名员工每日都比原先多生产1个零件，则现在日平均生产零件个数为 ___，方差为 ___．

5、某次跳绳比赛中，统计甲、乙两班学生每分钟跳绳的成绩（单位：次）情况如下表：

下列三个命题：

（1）甲班平均成绩低于乙班平均成绩；

（2）甲班成绩的波动比乙班成绩的波动大；

（3）甲班成绩优秀人数少于乙班成绩优秀人数．（跳绳次数次为优秀）

其中正确的命题是___________．（只填序号）

三、解答题（5小题，每小题10分，共计50分）

1、2020年冬季达州市持续出现雾霾天气．某记者为了了解“雾霾天气的主要成因”，随机调查了该市部分市民，并对调查结果进行整理，绘制了尚不完整的统计图表．

请根据图表中提供的信息解答下列问题：

（1）填空：m＝　   　，n＝　   　，扇形统计图中E组所占的百分比为 　   　%；

（2）若该市人口约有200万人，请你估计其中持D组“观点”的市民人数．

（3）治污减霾，你有什么建议？

2、对饮食健康越来越关注，特别关注食物的热量高低某校现在对学生食品的热量进行调查，随机从八、九年级中各随机抽取20名学生，对其食品热量进行整理、描述和分析（热量值用表示，共分为四个等级：A．，B．，C．，D．），下面给出了部分信息．

八年级20名学生食品的热量中B等级包含的所有数据为：

73，76，76，77，77，77，79．

九年级20名学生食品的热量是：64，64，66，68，69，70，72，74，77，78，80，82，85，85，85，85，86，93，96，101．

八、九年级抽取的学生食品热量统计表

根据以上信息，解答下列问题：

（1）填空：上述图表中____________， ____________．

（2）根据图表中的数据，判断八、九年级中哪个年级学生食品的热量更高？请说明理由（写出一条理由即可）；

（3）若该校八、九年级分别有1500，1600名学生，估计学生吃的食品的热量为A等级的学生共有多少人？

3、在推进城乡生活垃圾分类的行动中，社区从，两个小区各随机选择50位居民进行问卷调查，并得到他们的成绩，将成绩定为“不了解”，为“比较了解”，为“非常了解”，并绘制了如图的统计图：

（每一组不包含前一个边界值，包含后一个边界值）

已知小区共有常住居民500人，小区共有常住居民400人，

（1）请估计整个小区达到“非常了解”的居民人数．

（2）将“比较了解”和“非常了解”的人数作为普及到位的居民，请估计整个小区普及到位的居民人数．

（3）你认为哪个小区垃圾分类的普及工作更出色？请通过计算并用合适的数据来说明．

4、为了解中考体育科目训练情况，某区从全区九年级学生中随机抽取了部分学生进行了一次中考体育科目测试（把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格），并将测试结果绘成了如图、图2所示的两幅不完整的统计图，请根据统计中的信息解答下列问题：

（1）求本次抽样测试的学生人数是多少；

（2）通过计算把条形统计图补充完整；

（3）该区九年级有学生3500名，如果全部参加这次中考体育科目考试，请估计不及格的人数有多少人．

5、表格是小明一学期数学成绩的记录，根据表格提供的信息回答下面的问题．

（1）小明6次成绩的众数是_______分；中位数是_______分；

（2）计算小明平时成绩的方差；

（3）按照学校规定，本学期的综合成绩的权重如图所示，请你求出小明本学期的综合成绩，要写出解题过程.

（注意：①平时成绩用四次成绩的平均数；②每次考试满分都是100分）．

-参考答案-

一、单选题

1、B

【分析】

根据中位数不受极端值的影响即可得．

【详解】

解：由题得，去掉了一组数据的极端值，中位数不受极端值的影响，

故选B．

【点睛】

本题考查了一组数的特征数据，解题的关键是掌握平均数，中位数，众数，方差．

2、A

【详解】

解：A、共2+8+5+4+1=20人，中位数为10和11的平均数，故中位数为150元，故选项A不正确；

B、共20人，样本容量为20，故选项B正确；

C、极差为500﹣50=450元，故选项C正确；

D、该企业员工最大捐款金额是500元，故选项D正确．

故选：A ．

【点睛】

本题考查脂肪性获取信息，中位数，样本容量，极差，掌握相关概念是解题关键．

3、B

【分析】

先计算出九年级（3）班的全体人数，然后用选择“5G时代”的人数除以九年级（3）班的全体人数即可．

【详解】

由图知，九年级（3）班的全体人数为：25+30+10+20+15=100（人），
选择“5G时代”的人数为：30人，
∴选择“5G时代”的频率是：＝0.3；

故选：B．

【点睛】

本题考查了频数分布折线图，及相应频率的计算，熟知以上知识是解题的关键．

4、C

【分析】

根据极差和中位数的求解方法，求解即可，极差是一组数据中最大数减去最小数，中位数为是指一组数据从小到大排列，位于中间的那个数，数据个数为奇数时，中位数为中间的数，数据个数为偶数时，中位数为中间两数的平均值．

【详解】

解：成绩从小到大依次为：、、、、、、

极差为

中位数为

故选：C

【点睛】

此题考查了极差和中位数的计算，解题的关键是掌握极差和中位数的有关概念．

5、C

【分析】

根据组数=（最大值-最小值）÷组距计算即可．

【详解】

解：∵在样本数据中最大值与最小值的差为35-15=20，
又∵组距为4，
∵20÷4=5，
∴应该分成5+1=6组．
故选：C．

【点睛】

本题考查的是组数的计算，解题关键是明确用最大值减最小值的差除以组距可得组数．

6、B

【分析】

根据频数与频率的关系，审清题意频数之和等于所有数据的个数，频率之和等于1，即可得解．

【详解】

A. 频数分布表中，所有频率之和是1，故选项A不正确    ；

B. 频数之和等于所有数据的个数，故选项B正确；

C. 在频数分布表中，所有频数之和与所有数据的个数有关    ，故选项C不正确；

D. 在频数分布表中，所有频数之和等于所有数据的个数，故选项D不正确．

故选择B．

【点睛】

本题考查频数分布表中的频数与频率问题，频数之和等于总数，频率之和等于1，注意区分是解题关键．

7、D

【分析】

根据平均数、众数、中位数的定义以及方差公式计算即可得出答案．

【详解】

∵八年级5名参赛选手的成绩分别为：90，93，89，90，88，

从小到大排列为88，89，90，90，93，

∴平均数为，众数为90，中位数为90，

故选项A、B、C错误；

方差为，

故选项D正确．

故选：D．

【点睛】

本题考查平均数，众数和中位数，方差，掌握相关定义是解题的关键．

8、B

【分析】

根据平均数和方差的变化规律即可得出答案．

【详解】

∵a－1、b－1、c－1、d－1、e－1、f－1、g－1的平均数是m，方差是n，

∴数据a、b、c、d、e、f、g的平均数是m+1，方差是n，
∴2a-3、2b-3、2c-3、2d-3、2e-3、2f-3、2g-3的平均数是2（m+1）-3=2m-1；
∵数据a、b、c、d、e、f、g的方差是n，
∴数据2a-3、2b-3、2c-3、2d-3、2e-3、2f-3、2g-3的方差是22•n=4n；
故选：B．

【点睛】

本题考查了方差和平均数，当数据都加上一个数（或减去一个数）时，方差不变，即数据的波动情况不变，平均数也加或减这个数；当乘以一个数时，方差变成这个数的平方倍，平均数也乘以这个数．

9、A

【分析】

求出最大值和最小值的差，然后除以组距，用进一法取整数值就是组数．

【详解】

解：145-50=95，
95÷10=9.5，
所以应该分成10组．
故选A．

【点睛】

本题考查频率分布表中组数的确定，关键是求出最大值和最小值的差，然后除以组距，用进一法取整数值就是组数．

10、B

【分析】

此题有两个要求：①成绩较好，②状态稳定．于是应选平均数大、方差小的同学参赛．

【详解】

解：由于乙的方差较小、平均数较大，故选乙．

故选：B．

【点睛】

本题考查了平均数和方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．

二、填空题

1、2

【分析】

先由平均数的公式计算出x的值，再根据方差的公式计算．一般地设n个数据，x1，x2，…xn的平均数为 ， （x1+x2+…+xn），则方差 ．

【详解】

解：x=5×3-1-3-2-5=4，

s2= [（1-3）2+（3-3）2+（2-3）2+（5-3）2+（4-3）2]=2．

故答案为：2．

【点睛】

本题考查了方差的定义：一般地设n个数据，x1，x2，…xn的平均数为 ， （x1+x2+…+xn），则方差，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．

2、10℃

【分析】

用最高温度减去最低温度即可．

【详解】

解：该日的气温极差为22﹣12＝10（℃）．

故答案为：10℃．

【点睛】

本题考查了有理数减法，解题的关键是了解有理数减法法则在生活中运用方法，难度不大．

3、11

【分析】

根据极差=最大值-最小值求解可得．

【详解】

解：这组数据的最大值为19，最小值为8，

所以这组数据的极差为19-8=11，

故答案为：11．

【点睛】

本题主要考查极差，极差是指一组数据中最大数据与最小数据的差．

4、7    2.5   

【分析】

新数据是在原数据的基础上分别加上1所得，据此新数据的平均数在原数据平均数基础上加1，数据的波动幅度不变．

【详解】

解：根据题意，新数据是在原数据的基础上分别加上1所得，

所以现在日平均生产零件个数为6+1＝7，方差为2.5，

故答案为：7；2.5．

【点睛】

本题主要考查方差和平均数，解题的关键是根据题意得出新数据是在原数据的基础上分别加上1所得，据此新数据的平均数在原数据平均数基础上加1，数据的波动幅度不变．

5、（2）（3）

【分析】

平均数表示一组数据的平均程度，根据表示确定两班的平均成绩，进而判断说法（1）；由于方差是用来衡量一组数据波动大小的量，通过比较两班的方差，就能对（2）的说法进行分析；中位数是将一组数据从小到大(或从大到小）重新排列后，最中间的那个数(或最中间两个数的平均数)，进而判断（3）的正误．

【详解】

解：两个班的平均成绩均为135次，故（1）错误；

方差表示数据的波动大小，甲班的方差大于乙的，说明甲班的成绩波动大，故（2）正确；

中位数是数据按从小到大排列后，中间的数或中间两数的平均数，甲班的中位数小于乙班的，说明甲班学生成绩优秀人数不会多于乙班学生的成绩优秀的人数，故（3）正确．

综上可得三个说法中只有（2）（3）正确．

故答案为：（2）（3）．

【点睛】

本题考查了平均数、中位数、方差的意义，平均数表示一组数据的平均程度，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）；方差是用来衡量一组数据波动大小的量．

三、解答题

1、（1）400，100，15；（2）60万人；（3）见解析

【分析】

（1）根据A的人数除以BA所占的百分比，求得总人数，总人数乘以B的百分比可得m，总人数减去其余各组人数之和可得n，用E组人数除以总人数可得答案；

（2）根据全市总人数乘以D类所占比例，可得答案；

（3）根据以上图表提出合理倡议均可．

【详解】

解：（1）本次调查的总人数为80÷20%＝400（人），

则B组人数m＝400×10%＝40（人），

C组人数n＝400﹣（80+40+120+60）＝100（人），

∴扇形统计图中E组所占的百分比为（60÷400）×100%＝15%；

（2）200×＝60（万人），

答：估计其中持D组“观点”的市民人数有60万人；

（3）由上面的统计可知，造成“雾霾”的主要原因是“工厂造成的污染”和“汽车尾气排放”．

倡议关停重污染企业，加大对工厂排污的监管和处罚；倡议大家尽量乘坐公共交通工具出行，减少汽车尾气的排放．

【点睛】

本题主要考查了扇形统计图，统计表，能从图形中获取准确信息是解题的关键．

2、（1）78，85；（2）九年级学生食品热量更高，理由见解析；（3）780人

【分析】

（1）根据八年级的数据求得A等级人数，判断出中位数位于B等级，可求得a的值，根据众数的意义以及九年级的数据求得b；

（2）比较平均数、中位数可得结论；

（3）分别计算该校八、九年级学生的食品热量为A等级的百分比可得答案．

【详解】

解：（1）八年级学生食品的热量处于A等级人数20(人)，

∴八年级学生食品的热量的中位数位于B等级的第6、7两个数据，即77、79，

∴a=；

九年级20名学生食品的热量出现最多是85，共有4次，

∴a=85；

故答案为：78，85；

（2）九年级学生食品热量更高．

理由如下：由样本数据可得，八、九年级学生食品热量的平均数均为79，而八年级学生食品热量的中位数78，九年级学生食品热量的中位数79，79>78，所以九年级学生食品热量更高；

（3）由样本数据可得，

八年级学生的食品热量为A等级的有4人，占比﹔

九年级学生的食品热量为A等级的有6人，占比．

则两个年级共有（ 人）．

【点睛】

本题考查了中位数、众数、平均数的意义和计算方法，理解各个概念的内涵和计算方法，是解题的关键．

3、（1）96人；（2）250人；（3）B小区垃圾分类的普及工作更出色，见解析

【分析】

（1）用整个B小区总人数乘以样本中“非常了解”的人数的百分比，即可估计整个B小区达到“非常了解”的居民人数；

（2）用整个A小区总人数乘以样本中“比较了解”和“非常了解”的人数的频率，即可估计整个A小区普及到位的居民人数；

（3）计算出两个小区样本“不了解”的人数的百分比，用样本估计总体．

【详解】

解：（1）估计整个小区达到“非常了解”的居民人数有：（人）；

（2）整个小区普及到位的居民人数有：（人）；

（3）整个小区“不了解”的：；

整个小区“不了解”的44%．

因为44%<50%

所以小区垃圾分类的普及工作更出色．

【点睛】

本题考查了用样本估计总体，调查收集数据的过程与方法，解决本题的关键是掌握用样本估计总体．

4、（1）抽样测试的学生人数为40人；（2）条形统计图见详解；（3）估计不及格人数有700人

【分析】

（1）用B级人数除以B级人数占的百分比即可；

（2）用（1）中求得的数据乘以即可求出C级人数，然后补全统计图即可；

（3）用总人数乘以D级人数的比例即可．

【详解】

解：（1）（人），

∴本次抽样测试的学生人数是40人；

（2）（人），

∴抽样测试中为C级的人数是14人，

补全条形统计图，如图所示；

（3）（人），

∴估计不及格的人数有700人．

【点睛】

题目主要考查扇形统计图和条形统计图的综合，求样本总量，画条形统计图，用样本估计总体等，理解题意，数量掌握计算方法是解题关键．

5、（1）90，90；（2）小明平时成绩的方差；（3）小明本学期的综合成绩是93.5分．解题过程见解析．

【分析】

（1）根据众数和中位线的概念求解即可；

（2）先求出平时成绩的平均数，然后根据方差的计算公式代入求解即可；

（3）根据加权平均数的计算方法求解即可．

【详解】

解：（1）由表格可知，出现次数最多的90，

∴小明6次成绩的众数是90分；

把这6次成绩按从小到大排列为：86，88，90，90，92，96，

∴中间两个数为90，90，

∴中位数为：，

故答案为：90，90；

（2）平均分，

小明平时成绩的方差；

（3），

∴小明本学期的综合成绩是93.5分．

【点睛】

此题考查了平均数，中位数，众数，方差的计算等知识，解题的关键是熟练掌握平均数，中位数，众数，方差的计算方法．