2021-2022学年吉林省长春市新区七年级（上）期末数学试卷

2021-2022学年吉林省长春市新区七年级（上）期末数学试卷

1. 在0，，1，这四个数中，最小的数是

A.  B. 0 C. 1 D.

2. 2021年8月19日，由《环球时报》发起的“要求加拿大释放被美国迫害的中国公民！”联署活动，最终签名人数高达1400多万．经过中国政府不懈努力，9月25日，孟晚舟女士乘坐中国政府包机，回到祖国，将14000000这个数用科学记数法表示为

A.  B.  C.  D.

3. 把写成省略加号的和的形式是

A.  B.  C.  D.

4. 某正方体的每个面上都有一个汉字，如图是它的一种展开图，则在原正方体中，与“展”字所在面相对面上的汉字是

A. 长 B. 春 C. 新 D. 区

5. 下列计算正确的是

A.  B.
C.  D.

6. 如图所示，正方形网格中有和，如果每个小正方形的边长都为1，估测与的大小关系为

A.  B.  C.  D. 无法估测

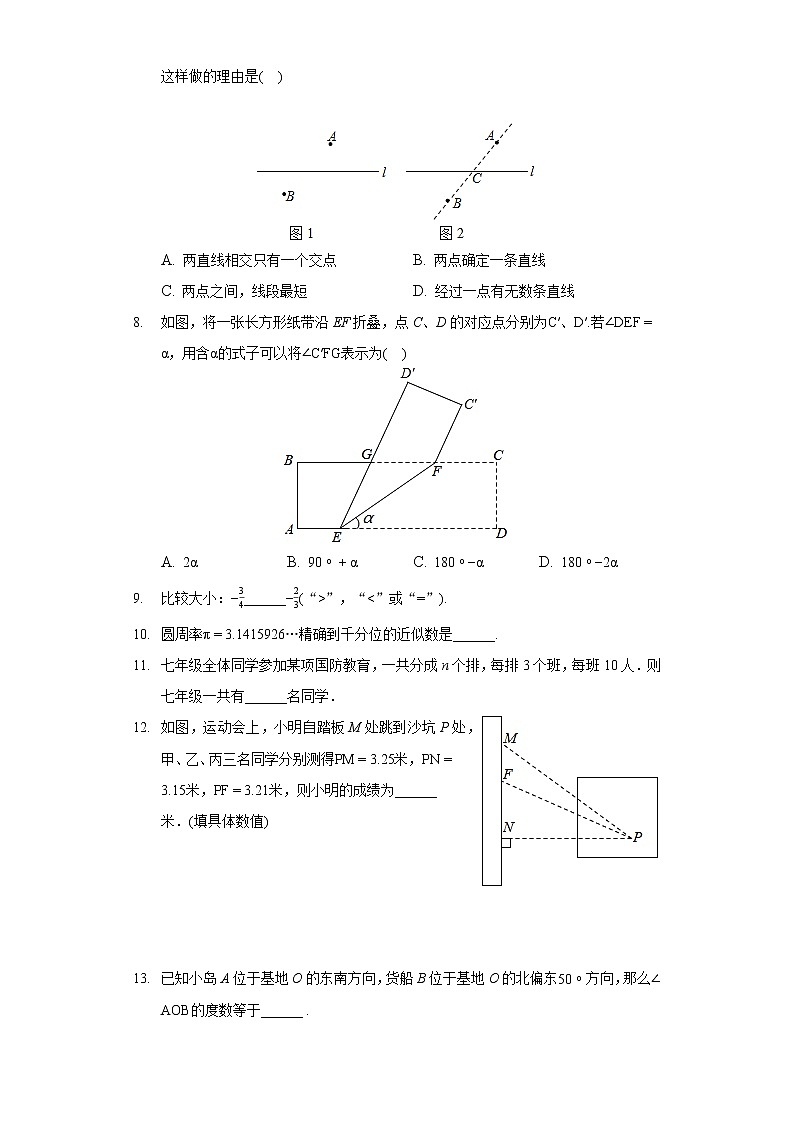
7. 如图1，A，B两个村庄在一条河不计河的宽度的两侧，现要建一座码头，使它到A、B两个村庄的距离之和最小，图2中所示的C点即为所求的码头的位置，那么这样做的理由是
    

A. 两直线相交只有一个交点 B. 两点确定一条直线
C. 两点之间，线段最短 D. 经过一点有无数条直线

8. 如图，将一张长方形纸带沿EF折叠，点C、D的对应点分别为、若，用含的式子可以将表示为

A.  B.  C.  D.

9. 比较大小：______“>”，“<”或“=”
10. 圆周率…精确到千分位的近似数是______.
11. 七年级全体同学参加某项国防教育，一共分成n个排，每排3个班，每班10人．则七年级一共有______名同学．
12. 如图，运动会上，小明自踏板M处跳到沙坑P处，甲、乙、丙三名同学分别测得米，米，米，则小明的成绩为______米．填具体数值
    
    
    
     

13. 已知小岛A位于基地O的东南方向，货船B位于基地O的北偏东方向，那么的度数等于______ .
14. 如图图案均是用相同的小木棒按一定的规律拼搭而成：拼搭第1个图案需7根小木棒，拼搭第2个图案需12根小木棒…依此规律，拼搭第n个图案需小木棒______根．
     

15. 计算：
    ；
    ；
    ；
    
    
    
    
    
    
    
     
16. 先化简，再求值：，其中，
    
    
    
    
    
    
     
17. 如图，已知点C为线段AB的中点，点D为线段BC的中点，，求线段AD的长度．
    
    
    
    
    
    
    
     
18. 如图，在的正方形网格中，每个小正方形的顶点称为格点，点D是的边BC上的一点，点M是内部的一点，点A、B、C、D、M均在格点上，只用无刻度的直尺，在给定的网格中按要求画图，并回答问题：
    过点M画BC的平行线MN交AB于点N；
    过点D画BC的垂线DE，交AB于点E；
    点E到直线BC的距离是线段______的长度．

19. 如图，如果，，，那么AB与CD平行吗？BC与DE呢？
    观察下面的解答过程，补充必要的依据或结论．
    解已知，
    ______，
    等量代换
    又已知，
    ______等式的性质，
    ______
    又______，
    等式的性质
    已知，
    ______，
    ______
    
    
    
    
    
    
     
20. 我国首个空间实验室“天宫一号”顺利升空．全国人民倍受鼓舞，某校开展了火箭模型制作比赛，如图为火箭模型的截面图，下面是梯形，中间是长方形，上面是三角形．
    用a、b的代数式表示该截面的面积S；
    当，时，求这个截面的面积．
    
    
     

21. 如图，直线AB、CD相交于O，，OF是的角平分线，，求的度数.

22. 如图，在表一中，将第1行第3列的数记为，则，将第3行第2列的数记为，则；按照要求回答下列各题：
    在表一中，______，______；
    在表一中，第3行第列的数可以记为______；
    如图，表二、表三、表四分别是从表一中截取的一部分，求的值．
     

23. 网约车已成为我们日常出行的一种便捷工具，某市网约车计价方式如表：

请你根据表信息计算：若小明乘坐网约车行驶千米，没有停车等待，则需付费______元；若行驶4千米，停车等待3分钟，则需付车费______元；
设行驶里程为x千米且为整数，停车等待时长为y分钟，则需付车费多少元？用含x、y的式子表示，并化简
李叔叔家离工作单位8千米，且从李叔叔家到工作单位的路上有3个红绿灯，其中每个红灯最长等待时间为1分钟．在不考虑堵车的前提下，请你计算李叔叔从家到工作单位乘坐网约车至少需付费多少元？最多付费多少元？






 

24. 小明同学遇到这样一个问题：
    如图①，已知：，E为AB、CD之间一点，连接BE，ED，得到
    求证：
    小亮帮助小明给出了该问的证明．
    证明：
    过点E作，则有
    ，
    ，
    ，
    
    请你参考小亮的思考问题的方法，解决问题：
    直线，直线EF和直线、分别交于C、D两点，点A、B分别在直线、上，
    猜想：如图②，若点P在线段CD上，，，求的度数．
    拓展：如图③，若点P在直线EF上，连接PA、，直接写出、、之间的数量关系．
     

答案和解析

1.【答案】D
 

【解析】解：，
在0，，1，这四个数中，最小的数是
故选：
依据比较有理数大小的法则进行比较即可．
本题考查了对有理数的大小比较法则的应用，注意：正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小．
 

2.【答案】C
 

【解析】解：将14000000科学记数法表示为，
故选：
科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值时，n是正数；当原数的绝对值时，n是负数．
此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，n为整数，表示时关键要正确确定a的值以及n的值．
 

3.【答案】B
 

【解析】解：，
故选：
利用减法法则把减法化为加法写成省略加号的和的形式．
本题主要考查了有理数的加减混合运算，掌握把有理数加减法统一成加法是解题关键．
 

4.【答案】C
 

【解析】解：在原正方体中，与“展”字所在面相对面上的汉字是新，
故选：
根据正方体的平面展开图找相对面的方法，”Z“字两端是对面，判断即可．
本题考查了正方体相对两个面上的文字，根据正方体的平面展开图找相对面是解题的关键．
 

5.【答案】D
 

【解析】解：A、不是同类项，不能合并，选项错误；
B、，选项错误；
C、不是同类项，不能合并，选项错误；
D、，选项正确．
故选：
根据合并同类项的法则即可作出判断．
本题主要考查了合并同类项的法则，即系数相加作为系数，字母和字母的指数不变．
 

6.【答案】A
 

【解析】解：将平移，使与两个角的顶点重合，
可得：在的内部，
所以，
故选：
将平移，让与两个角的顶点重合，即可解答．
本题考查了角的大小比较，利用平移的方法是解题的关键．
 

7.【答案】C
 

【解析】解：A，B两个村庄在一条河不计河的宽度的两侧，现要建一座码头，使它到A、B两个村庄的距离之和最小，图2中所示的C点即为所求的码头的位置，那么这样做的理由是两点之间，线段最短，
故选：C。
利用线段的性质解答即可．
此题主要考查了线段的性质，关键是掌握两点之间，线段最短。
 

8.【答案】D
 

【解析】解：由长方形纸带ABCD及折叠性质可得：，，
，，
，
，

故选：
由折叠的性质可得：，，由可得，从而有，即可得出结果．
本题主要考查平行线的性质，折叠的性质，解答的关键是熟记折叠的性质．
 

9.【答案】<
 

【解析】解：，，而，

故答案为：
两个负数比较大小，绝对值大的其值反而小，据此判断即可．
本题考查了有理数大小比较，要熟练掌握并正确运用有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数比较大小，绝对值大的其值反而小．
 

10.【答案】
 

【解析】解：圆周率…精确到千分位的近似数是
故答案为
近似数…精确到千分位，即是保留到千分位，由于千分位1后面的5大于4，故进1，得
本题考查了近似数和精确度，精确到哪一位，就是对它后边的一位进行四舍五入．
 

11.【答案】30n
 

【解析】解；七年级一共有30n名同学；
故答案为：30n
根据题意列出代数式解答即可．
此题主要考查了列代数式，关键是注意代数式的写法．
 

12.【答案】
 

【解析】解：小明的成绩是点P到直线MN的距离，即PN，
小明的成绩为米．
故答案为：
根据垂线段最短即可得出结论．
本题考查的是垂线段最短，熟知“垂线段最短”是解答此题的关键．
 

13.【答案】
 

【解析】解：如图：，
，
，
，
故答案为：
根据方位角的概念，画图正确表示出A，B的方位，易得结果．
本题主要考查了方位角的概念，根据方位角的概念，画图正确表示出A，B的方位，注意东南方向是是解答此题的关键．
 

14.【答案】
 

【解析】解：分析可得：第1个图形中，有根木棒；
第2个图形中，有根木棒；
第3个图形中，有根木棒；
…
第n个图形中，共用木棒的根数是
故答案为：
分析可得：第1个图案需要小木棒根，第二个图案需要根，第三个图案需要根，…，继而即可找出规律，求出第n个图案需要小木棒的根数．
此题主要考查学生对图形变化类这个知识点的理解和掌握，解答此类题目的关键是根据题目中给出的图形，通过观察思考，归纳总结出规律，此类题目难度一般偏大，属于难题．
 

15.【答案】解：原式

；
原式


；
原式

；
原式



 

【解析】根据有理数的加法交换律和结合律计算即可；
根据有理数的加法交换律和结合律计算即可；
利用乘法分配律展开，再进一步计算即可；
先计算乘方，再计算除法，继而计算乘法，最后计算减法即可．
本题主要考查有理数的混合运算，解题的关键是掌握有理数的混合运算顺序和运算法则．
 

16.【答案】解：原式
，
，，
原式



 

【解析】原式去括号合并得到最简结果，再把x与y的值代入计算即可求出值．
本题考查了整式的加减-化简求值，涉及去括号法则，同类项的定义，合并同类项法则等知识，熟练掌握运算法则是解本题的关键．
 

17.【答案】解：，C是AB中点，
，
是BC中点，
，

 

【解析】根据，分别求出AC、CD即可解决问题．
本题考查两点间的距离、线段的中点等知识，解题的关键是熟练掌握基本概念，属于中考常考题型．
 

18.【答案】DE
 

【解析】解：如图，直线MN即为所求；
如图，直线DE即为所求；
点E到直线BC的距离是线段ED的长度．
故答案为：

根据平行线的定义作出图形即可；
根据垂线的定义作出图形即可；
根据垂线段的定义作出图形即可．
本题考查作图-应用与设计作图，点到直线的距离，平行线的判定和性质等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．
 

19.【答案】对顶角相等  同旁内角互补，两直线平行  180 等量代换  内错角相等，两直线平行
 

【解析】解已知，
对顶角相等，
等量代换
又已知，
等式的性质，
同旁内角互补，两直线平行
又，
等式的性质
已知，
等量代换，
内错角相等，两直线平行
故答案为：对顶角相等；；同旁内角互补，两直线平行；180；等量代换；内错角相等，两直线平行．
由对顶角相等可得，从而可求，利用平行线的判定条件可得，由已知条件可得，从而有，从而可判定
本题主要考查平行线的判定与性质，解答的关键是熟记平行线的判定条件及性质并灵活运用．
 

20.【答案】解：，
，
，
；
当，时，




答：当，时，这个截面的面积为
 

【解析】利用三角形，长方形，梯形的面积公式分别计算三部分的面积再相加即可；
将a，b的值代入中的代数式计算即可．
本题主要考查了列代数式，求代数式的值，利用三角形，长方形，梯形的面积公式分别计算三部分的面积是解题的关键．
 

21.【答案】解：，，
，
又平分，
，
，
，
则
 

【解析】利用角的和差关系和角平分线定义可得的度数，然后计算出的度数，再根据对顶角相等可得的度数．
本题考查的是角平分线的定义、余角和补角，对顶角，掌握它们的概念是解题的关键．
 

22.【答案】
 

【解析】解：第三行数的规律是3n，
第三行第五个数是15，
，
第8行数的规律是8n，
第8行第10个数是80，
，
故答案为：15，80；
第三行数的规律是3n，
，
故答案为：；
表2中，，，
是第6行第3个数，
，
表3中，20和25在同一行，
是第5行第4个数，
是第6行第5个数，
，
表4中，18是第6行第3个数，21是第7行第3个数，
是第7行第4个数，
，

通过观察可知第三行数的规律是3n，第8行数的规律是8n；
由第三行数的规律是3n，可求解；
是第6行第3个数，b是第6行第5个数，c是第7行第4个数，分别求出a、b、c，再代入所求代数式即可．
本题考查数字的变化规律，能够通过所给表格，找到行、列各数字之间的规律是解题的关键．
 

23.【答案】
 

【解析】解：小明乘坐网约车行驶千米，没有停车等待，需要付费6元；
行驶4千米，停车等待3分钟，则需付车费：元，
故答案为：6，；
需付车费为：元，
答：需付车费元；
至少的付费则当没有停车等待时，得：
元，
最多的付费则每个红灯都等待最长的时间时，得：


元
答：至少需付费元，最多付费元．
根据计价方式进行求解即可；
根据计价方式进行求解即可；
至少的付费则没有停车等待时，最多的付费则每个红灯都等待最长的时间时，据此列方程作答即可．
本题主要考查一元一次方程的应用，解答的关键是理解清楚题意，找到等量关系列出方程．
 

24.【答案】解：猜想：如图1，过点P作，则，
，
，
，
，
，，

拓展：①如图1，当点P在线段CD上时，
由猜想可知，；
②如图2，当点P在射线DP上时，
过点P作，则，
，
，
，
；
③如图3，当点P在射线CE上时，
过点P作，则，
，
，
，
；
综上所述，、、之间的数量关系为或或
 

【解析】猜想：过点P作，然后得到，从而得到，，然后得到的度数；
拓展：分情况讨论，当点P在线段CD上时，当点P在射线DF上时，当点P在射线CE上时，然后过点P作，再利用平行线的性质进行探究角之间的数量关系．
本题考查了平行线的性质，解题的关键是熟练作出辅助线构造平行线，然后通过平行线的性质得到内错角相等．