【真题汇总卷】2022年北京市怀柔区中考数学备考真题模拟测评 卷（Ⅰ）（含答案详解）

2022年北京市怀柔区中考数学备考真题模拟测评 卷（Ⅰ）

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、下列图形是中心对称图形的是（    ）．

A． B．

C． D．

2、若，则的值是（    ）

A． B．0 C．1 D．2022

3、下列图形中，是中心对称图形的是（    ）

A． B．

C． D．

4、下列运动中，属于旋转运动的是（    ）

A．小明向北走了 4 米 B．一物体从高空坠下

C．电梯从 1 楼到 12 楼 D．小明在荡秋千

5、如图，将△ABC绕点C按逆时针方向旋转至△DEC，使点D落在BC的延长线上．已知∠A＝32°，∠B＝30°，则∠ACE的大小是（    ）

A．63° B．58° C．54° D．56°

6、如图，五边形ABCDE中有一正三角形ACD，若AB=DE，BC=AE，∠E=108°则∠BAE的度数为（　　）

A．120° B．108° C．132° D．72°

7、某公园改造一片长方形草地，长增加30%，宽减少20%，则这块长方形草地的面积（      ）

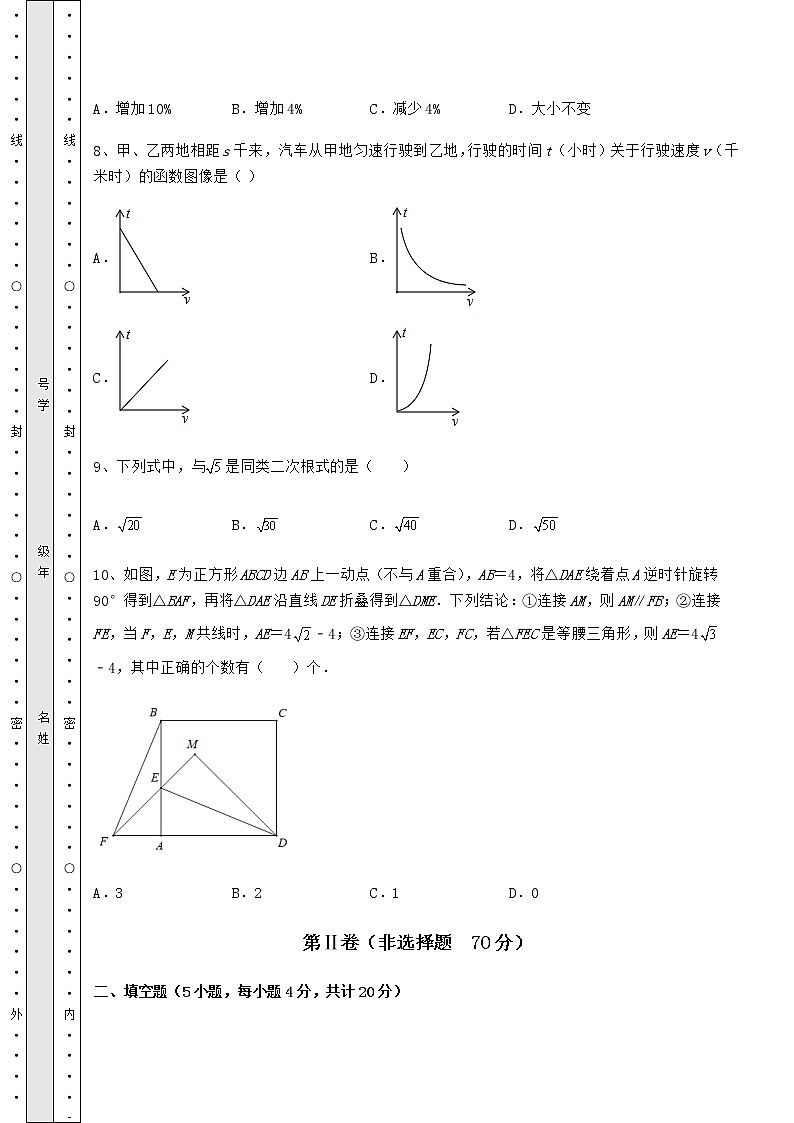
A．增加10% B．增加4% C．减少4% D．大小不变

8、甲、乙两地相距s千来，汽车从甲地匀速行驶到乙地，行驶的时间t（小时）关于行驶速度v（千米时）的函数图像是（ ）

A． B．

C． D．

9、下列式中，与是同类二次根式的是（　　）

A． B． C． D．

10、如图，E为正方形ABCD边AB上一动点（不与A重合），AB＝4，将△DAE绕着点A逆时针旋转90°得到△BAF，再将△DAE沿直线DE折叠得到△DME．下列结论：①连接AM，则AM∥FB；②连接FE，当F，E，M共线时，AE＝4﹣4；③连接EF，EC，FC，若△FEC是等腰三角形，则AE＝4﹣4，其中正确的个数有（　　）个．

A．3 B．2 C．1 D．0

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、如图，l1∥l2∥l3，若AB＝2，BC＝3，AD＝1，CF＝4，则BE的长为______．

2、比较大小：－7______－8（填入＞”或“＜”号）．．

3、要使成为完全平方式，那么b的值是______．

4、如图，四边形中，，，，在、上分别找一点M、N，当周长最小时，的度数是______________．

5、如图，将△ABC绕点A顺时针旋转，使点C落在边AB上的点E处，点B落在点D处，联结BD，如果∠DAC＝∠DBA，那么∠BAC＝___度．

三、解答题（5小题，每小题10分，共计50分）

1、如图，在平面直角坐标系xOy中，△ABC是等腰直角三角形，∠BAC＝90°，A（1，0），B（0，2），二次函数y＝x2+bx﹣2的图象经过C点．

（1）求二次函数的解析式；

（2）若点P是抛物线的一个动点且在x轴的下方，则当点P运动至何处时，恰好使△PBC的面积等于△ABC的面积的两倍．

（3）若点Q是抛物线上的一个动点，则当点Q运动至何处时，恰好使∠QAC＝45°？请你求出此时的Q点坐标．

2、如图，射线、、、分别表示从点出发的向北、东、南、西四个方向，将直角三角尺的直角顶点与点重合．

（1）图中与互余的角是_______；

（2）①用直尺和圆规作的平分线；（不写作法，保留作图痕迹）

②在①所做的图形中，如果，那么点在点的_______方向．

3、如图，一次函数的图象与反比例函数的图象交于A，B两点，且与y轴交于点C，点A的坐标为．

（1）求m及k的值；

（2）求点B的坐标及的面积；

（3）观察图象直接写出使反比例函数值大于一次函数值的自变量x取值范围．

4、解方程：．

5、如图，一次函数与反比例函数（k≠0）交于点A、B两点，且点A的坐标为（1，3），一次函数与轴交于点C，连接OA、OB．

（1）求一次函数和反比例函数的表达式；

（2）求点B的坐标及的面积；

（3）过点A作轴的垂线，垂足为点D．点M是反比例函数第一象限内图像上的一个动点，过点M作轴的垂线交轴于点N，连接CM．当与Rt△CNM相似时求M点的坐标．

-参考答案-

一、单选题

1、A

【分析】

把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，据此可得结论．

【详解】

解：选项B、C、D均不能找到这样的一个点，使图形绕某一点旋转180°后与原来的图形重合，所以不是中心对称图形，

选项A能找到这样的一个点，使图形绕某一点旋转180°后与原来的图形重合，所以是中心对称图形，

故选：A．

【点睛】

本题主要考查了中心对称图形，掌握中心对称图形的定义是解题关键．

2、C

【分析】

先根据非负数的性质求出a和b的值，然后代入所给代数式计算即可．

【详解】

解：∵，

∴a-2=0，b+1=0，

∴a=2，b=-1，

∴=，

故选C．

【点睛】

本题考查了非负数的性质，以及求代数式的值，根据非负数的性质求出a和b的值是解答本题的关键．

3、B

【分析】

根据中心对称图形的定义求解即可．

【详解】

解：A、不是中心对称图形，不符合题意；

B、是中心对称图形，符合题意；

C、不是中心对称图形，不符合题意；

D、不是中心对称图形，不符合题意．

故选：B．

【点睛】

此题考查了中心对称图形，解题的关键是熟练掌握中心对称图形的定义．中心对称图形：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形．

4、D

【分析】

旋转定义：物体围绕一个点或一个轴作圆周运动，根据旋转定义对各选项进行一一分析即可．

【详解】

解：A. 小明向北走了 4 米，是平移，不属于旋转运动，故选项A不合题意；   

B. 一物体从高空坠下，是平移，不属于旋转运动，故选项B不合题意；   

C. 电梯从 1 楼到 12 楼，是平移，不属于旋转运动，故选项C不合题意；   

D. 小明在荡秋千，是旋转运动，故选项D符合题意．

故选D．

【点睛】

本题考查图形旋转运动，掌握旋转定义与特征，旋转中心，旋转方向，旋转角度是解题关键．

5、C

【分析】

先根据三角形外角的性质求出∠ACD=63°，再由△ABC绕点C按逆时针方向旋转至△DEC，得到△ABC≌△DEC，证明∠BCE=∠ACD，利用平角为180°即可解答．

【详解】

解：∵∠A=33°，∠B=30°，

∴∠ACD=∠A+∠B=33°+30°=63°，

∵△ABC绕点C按逆时针方向旋转至△DEC，

∴△ABC≌△DEC，

∴∠ACB=∠DCE，

∴∠BCE=∠ACD，

∴∠BCE=63°，

∴∠ACE=180°-∠ACD-∠BCE=180°-63°-63°=54°．

故选：C．

【点睛】

本题考查了旋转的性质，三角形外角的性质，解决本题的关键是由旋转得到△ABC≌△DEC．

6、C

【分析】

根据等边三角形的性质可得，，然后利用SSS即可证出，从而可得，，，然后求出，即可求出的度数．

【详解】

解：△是等边三角形，

，，

在与中

，

，

，，，

，

，

故选C

【点睛】

此题考查的是等边三角形的性质和全等三角形的判定及性质，掌握等边三角形的性质、利用SSS判定两个三角形全等和全等三角形的对应角相等是解决此题的关键．

7、B

【分析】

设长方形草地的长为x，宽为y，则可求得增加后长及减少后的宽，从而可求得现在的面积，与原面积比较即可得到答案．

【详解】

设长方形草地的长为x，宽为y，则其面积为xy；增加后长为(1+30%)x，减少后的宽为(1-20%)y，此时的面积为(1+30%)x×(1-20%)y=1.04xy，1.04xy−xy=0.04xy，0.04xy÷xy×100%=4%．即这块长方形草地的面积比原来增加了4%．

故选：B

【点睛】

本题考查了列代数式，根据题意设长方形草地的长与宽，进而求得原来的面积及长宽变化后的面积是关键．

8、B

【分析】

直接根据题意得出函数关系式，进而得出函数图象．

【详解】

解：由题意可得：t=，是反比例函数，

故只有选项B符合题意．

故选：B．

【点睛】

此题主要考查了反比例函数的应用，正确得出函数关系式是解题关键．

9、A

【分析】

先根据二次根式的性质化成最简二次根式，再看看被开方数是否相同即可．

【详解】

解：A、，即化成最简二次根式后被开方数相同（都是5），所以是同类二次根式，故本选项符合题意；

B、最简二次根式和的被开方数不相同，所以不是同类二次根式，故本选项不符合题意；

C、，即化成最简二次根式后被开方数不相同，所以不是同类二次根式，故本选项不符合题意；

D、，即化成最简二次根式后被开方数不相同，所以不是同类二次根式，故本选项不符合题意；

故选：A．

【点睛】

本题考查了二次根式的性质与化简和同类二次根式的定义，能熟记同类二次根式的定义是解此题的关键．

10、A

【分析】

①正确，如图1中，连接AM，延长DE交BF于J，想办法证明BF⊥DJ，AM⊥DJ即可；

②正确，如图2中，当F、E、M共线时，易证∠DEA=∠DEM=67.5°，在MD上取一点J，使得ME=MJ，连接EJ，设AE=EM=MJ=x，则EJ=JD=x，构建方程即可解决问题；

③正确，如图3中，连接EC，CF，当EF=CE时，设AE=AF=m，利用勾股定理构建方程即可解决问题．

【详解】

解：①如下图，连接AM，延长DE交BF于J，

∵四边形ABCD是正方形，

∴AB=AD，∠DAE=∠BAF=90°，

由题意可得AE=AF，

∴△BAF≌△DAE(SAS)，

∴∠ABF=∠ADE，

∵∠ADE+∠AED=90°，∠AED=∠BEJ，

∴∠BEJ+∠EBJ=90°，

∴∠BJE=90°，

∴DJ⊥BF，

由翻折可知：EA=EM，DM=DA，

∴DE垂直平分线段AM，

∴BF∥AM，故①正确；

②如下图，当F、E、M共线时，易证∠DEA=∠DEM=67.5°，

在MD上取一点J，使得ME=MJ，连接EJ，

则由题意可得∠M=90°，

∴∠MEJ=∠MJE=45°，

∴∠JED=∠JDE=22.5°，

∴EJ=JD，

设AE=EM=MJ=x,则EJ=JD=x，

则有x+x =4，

∴x=4﹣4，

∴AE=4﹣4，故②正确；

③如下图，连接CF，

当EF=CE时，设AE=AF=m，

则在△BCE中，有2m²=4²+(4-m)2，

∴m=4﹣4或-4﹣4 (舍弃)，

∴AE=4﹣4，故③正确；

故选A．

【点睛】

本题考查旋转变换，翻折变换，正方形的性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，学会利用参数构建方程解决问题，属于中考选择题中的压轴题．

二、填空题

1、

【分析】

由题意知；如图过点作交于点，交于点；有四边形 与四边形均为平行四边形，且有， ，；；可得的值，由可知的值．

【详解】

解：如图过点作交于点，交于点；

四边形 与四边形均为平行四边形

， ，

由题意知

故答案为：．

【点睛】

本题考查了平行线分线段成比例，平行四边形的性质，三角形相似等知识点．解题的关键在于作辅助线将平行线分线段成比例应用于相似三角形中找出线段的关系．

2、

【分析】

根据两个负数比较大小，其绝对值大的反而小比较即可．

【详解】

解：，，

，

，

故答案为：．

【点睛】

本题考查了绝对值和有理数的大小比较，解题的关键是能熟记有理数的大小比较法则的内容，注意：两个负数比较大小，其绝对值大的反而小．

3、

【分析】

根据完全平方式的性质：，可得出答案.

【详解】

∵是完全平方式

∴

解得

故答案为.

【点睛】

本题考查完全平方式，熟记完全平方式的形式，找出公式中的a和b的关键.

4、128°

【分析】

分别作点A关于BC、DC的对称点E、F，连接EF、DF、BE ，则当M、N在线段EF上时△AMN的周长最小，此时由对称的性质及三角形内角和定理、三角形外角的性质即可求得结果．

【详解】

分别作点A关于BC、DC的对称点E、F，连接EF、DF、BE，如图

由对称的性质得：AN=FN，AM=EM

∴∠F=∠NAD，∠E=∠MAB

∵AM+AN+MN=EM+FN+MN≥EF

∴当M、N在线段EF上时，△AMN的周长最小

∵∠AMN+∠ANM=∠E+∠MAB+∠F+∠NAD=2∠E+2∠F=2(∠E+∠F)=2(180°−∠BAD)=2×(180°−116°)=128°

故答案为：128°

【点睛】

本题考查了对称的性质，两点间线段最短，三角形内角和定理与三角形外角的性质等知识，作点A关于BC、DC的对称点是本题的关键．

5、36

【分析】

设∠BAC=x，依据旋转的性质，可得∠DAE=∠BAC=x，∠ADB=∠ABD=2x，再根据三角形内角和定理即可得出x．

【详解】

解：设∠BAC=x，由旋转的性质，可得

∠DAE=∠BAC=x，

∴∠DAC=∠DBA=2x，

又∵AB=AD，

∴∠ADB=∠ABD=2x，

△ABD中，∠BAD+∠ABD+∠ADB=180°，

∴x+2x+2x=180°，

∴x=36°，

即∠BAC=36°，

故答案为：36．

【点睛】

本题主要考查了旋转的性质以及三角形内角和定理，解题时注意：旋转前、后的图形全等．

三、解答题

1、（1）；（2）当点P运动至坐标为或时，恰好使△PBC的面积等于△ABC的面积的两倍； （3）或

【分析】

（1）如图，过作于 先证明 可得 再代入二次函数y＝x2+bx﹣2中，再利用待定系数法求解即可；

（2）先求解 过作轴交于 再求解直线为： 设 则 再利用 再解方程即可；

（3）分两种情况讨论：如图，作关于的对称点 连接 作的角平分线 交于 交抛物线于 由 则再求解的解析式，再求解与抛物线的交点坐标即可，如图，同理可得：当平分时，射线与抛物线的交点满足 按同样的方法可得答案.

【详解】

解：（1）如图，过作于

则 而

而

二次函数y＝x2+bx﹣2的图象经过C点，

解得：

二次函数的解析式为：

（2）

过作轴交于

设直线为

解得：

所以直线为：

设 则

整理得：

解得：

当时，

当时，

或

所以当点P运动至坐标为或时，恰好使△PBC的面积等于△ABC的面积的两倍．

（3）如图，作关于的对称点 连接 作的角平分线 交于 交抛物线于

由 则

平分

则

同理可得直线的解析式为：

解得：或（不合题意，舍去）

如图，同理可得：当平分时，射线与抛物线的交点满足

同理：

直线为：

解得：或（不合题意舍去）

【点睛】

本题考查的是利用待定系数法求解一次函数，二次函数关系式，全等三角形的性质与判定，等腰直角三角形的性质，一元二次方程的解法，清晰的分类讨论是解本题的关键.

2、

（1）、

（2）①作图见解析；②北偏东或东偏北

【分析】

（1）由题可知，故可知与互余的角；

（2）①如图所示，以O为圆心画弧，分别与OE、OA相交；以两交点为圆心，大于两点长度的一半为半径画弧，连接两弧交点与O点的射线即为角平分线；②，，进而得出P与O有关的位置．

（1）

解：图中与互余的角是和；

故答案为：、．

（2）

①如图，为所作；

②，

，

平分，

，

，

即点在点的北偏东方向或东偏北

故答案为：北偏东或东偏北．

【点睛】

本题考查了余角，角平分线以及坐标系中的位置．解题的关键在于正确的求解角度．

3、

（1）m＝﹣3，k＝2；

（2）（﹣，﹣4），；

（3）或．

【分析】

（1）把A点的坐标代入函数解析式，即可求出答案；

（2）解由两函数解析式组成的方程组，求出方程组的解，即可得出B点的坐标，求出C点的坐标，再根据三角形面积公式求即可；

（3）求出C的坐标，根据图形即可求出答案．

（1）

解：∵点A（2，1）在函数y＝2x+m的图象上，

∴4+m＝1，即m＝﹣3，

∵A（2，1）在反比例函数的图象上，

∴，

∴k＝2；

所以m＝﹣3，k＝2；

（2）

解：∵一次函数解析式为y＝2x﹣3，令x＝0，得y＝-3，

∴点C的坐标是（0，-3），

∴OC＝3，

联立方程组得，得：或，

∴点B的坐标为（﹣，﹣4），

∴S△AOB＝S△AOC+S△BOC＝；

（3）

解：观察图象可知，在第三象限时，在点B左侧或在第一象限时，在点A左侧时，反比例函数值大于一次函数值，故自变量x取值范围为或．

【点睛】

本题考查了待定系数法求出一次函数和反比例函数的解析式、两函数的交点问题和函数的图象等知识点，能求出两函数的解析式是解此题的关键，用了数形结合思想．

4、

【分析】

先去分母，去括号，再移项、合并同类项，最后系数化为1即可得答案．

【详解】

去分母得：，

去括号得：，

移项得：，

合并同类项得：，

系数化1得：．

【点睛】

本题考查解一元一次方程，熟练掌握解一元一次方程的一般步骤是解题关键．

5、（1）一次函数表达式为，反比例函数表达式为；（2），；（3）或

【分析】

（1）把分别代入一次函数与反比例函数，解出，即可得出答案；

（2）把一次函数和反比例函数联立求解即可求出点B坐标，令代入一次函数解出点C坐标，由即可；

（3）根据相似三角形的判定：两边成比例且夹角相等的两个三角形相似，找出对应边成比例求解即可．

【详解】

（1）把代入一次函数得：，

解得：，

∴一次函数表达式为，

把代入反比例函数得：，即，

∴反比例函数表达式为；

（2），

解得：或，

∴，

令代入得：，

∴，

∴；

（3）

①当时，，

，，，，

∴，即，

解得：，，

∵M在第一象限，

∴，，

∴，

②当时，，

∴，即，

解得：，，

∵M在第一象限，

∴，，

∴，

综上，当与相似时，M点的坐标为或．

【点睛】

本题考查反比例函数综合以及相似三角形的判定与性质，掌握相关知识点的应用是解题的关键．