专题12.20 三角形全等几何模型-“手拉手”模型（专项练习）（基础篇）-2021-2022学年八年级数学上册基础知识专项讲练（人教版）

专题12.20 三角形全等几何模型-“手拉手”模型

（专项练习）（基础篇）

一、单选题

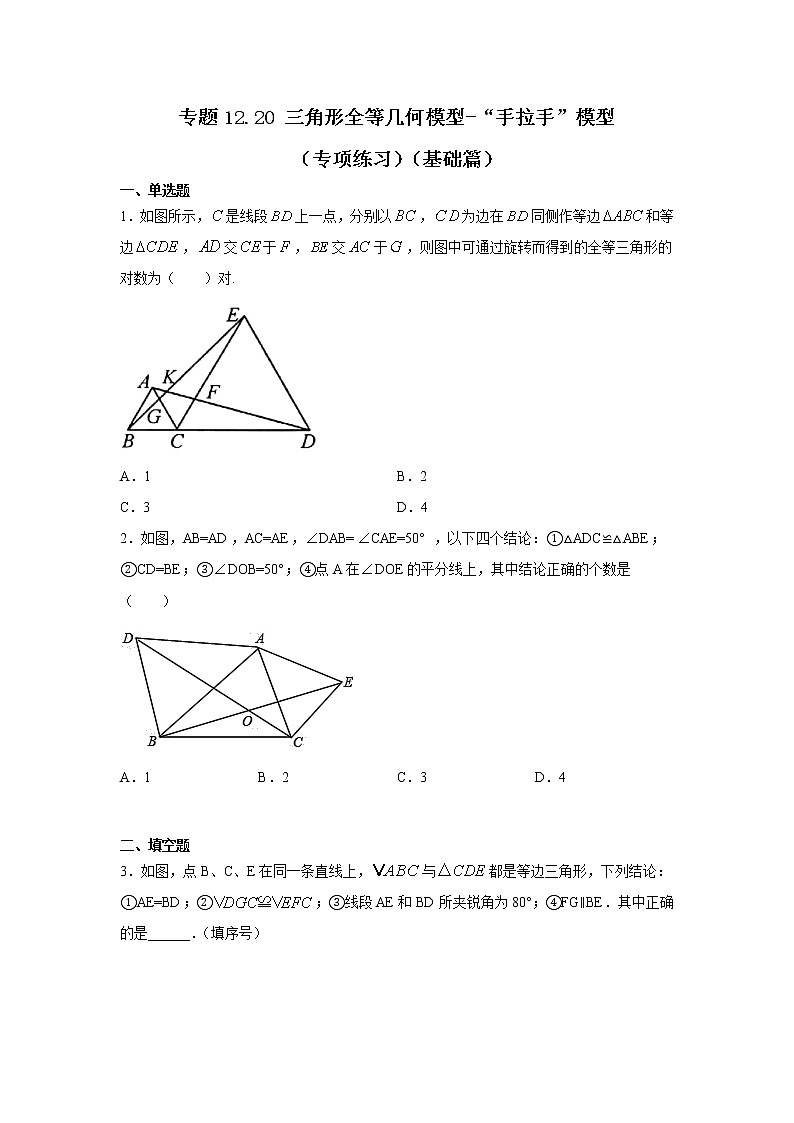
1．如图所示，是线段上一点，分别以，为边在同侧作等边和等边，交于，交于，则图中可通过旋转而得到的全等三角形的对数为（    ）对.

A．1 B．2

C．3 D．4

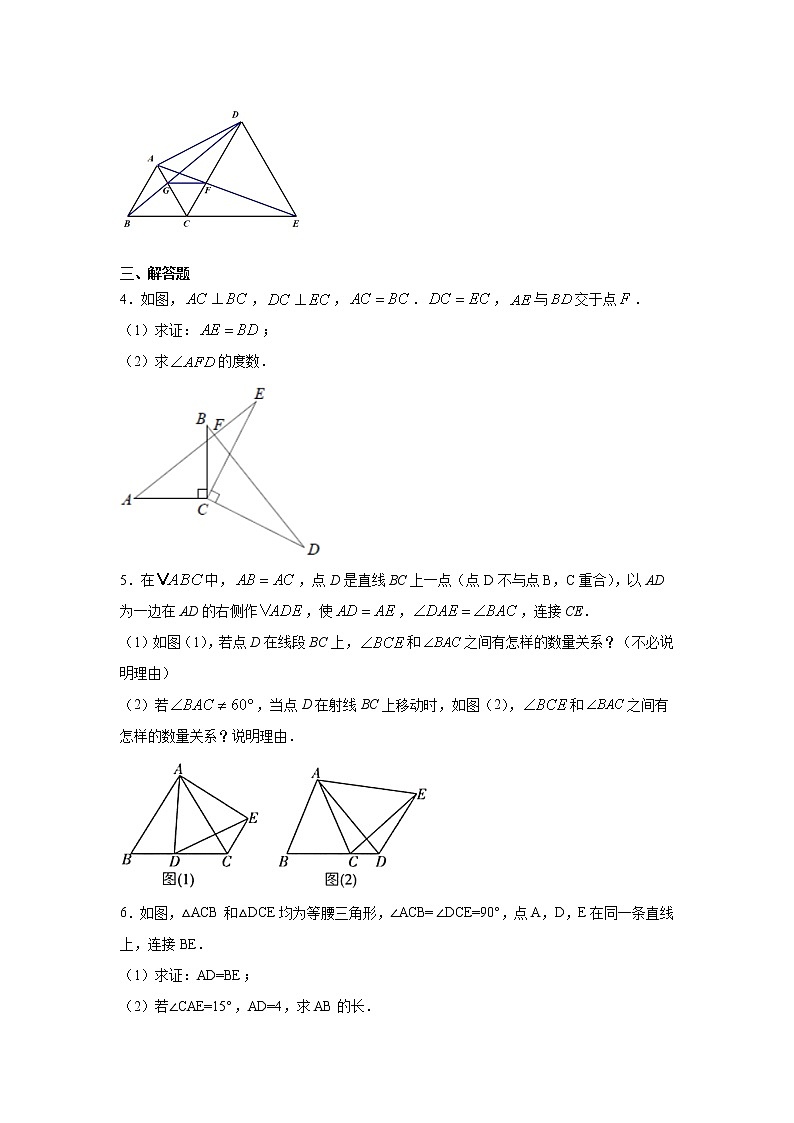
2．如图，AB=AD，AC=AE，DAB=CAE=50° ，以下四个结论：①△ADC≌△ABE；②CD=BE；③DOB=50°；④点A在DOE的平分线上，其中结论正确的个数是（    ）

A．1 B．2 C．3 D．4

二、填空题

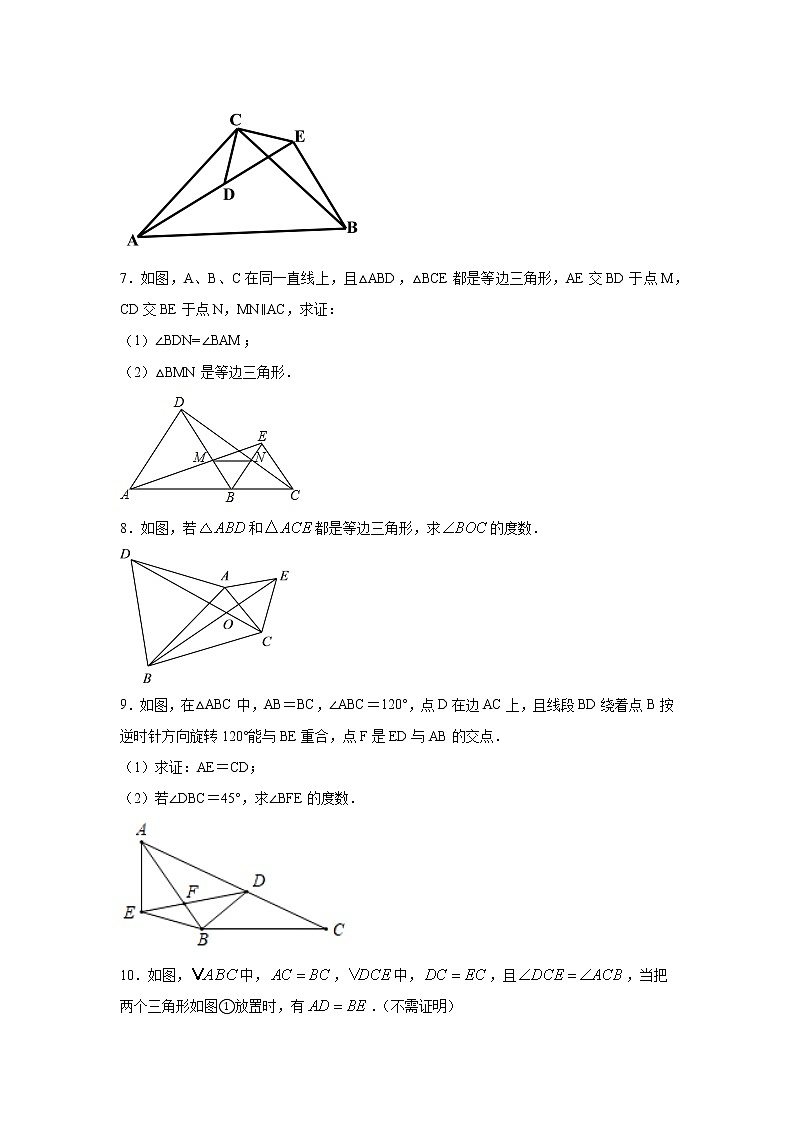
3．如图，点B、C、E在同一条直线上，与都是等边三角形，下列结论：①AE=BD；②；③线段AE和BD所夹锐角为80°；④FG∥BE．其中正确的是______．（填序号）

三、解答题

4．如图，，，．，与交于点．

（1）求证：；

（2）求的度数．

5．在中，，点D是直线BC上一点（点D不与点B，C重合），以AD为一边在AD的右侧作，使，，连接CE．

（1）如图（1），若点D在线段BC上，和之间有怎样的数量关系？（不必说明理由）

（2）若，当点D在射线BC上移动时，如图（2），和之间有怎样的数量关系？说明理由．

6．如图，△ACB和△DCE均为等腰三角形，∠ACB=∠DCE=90°，点A，D，E在同一条直线上，连接BE．

（1）求证：AD=BE；

（2）若∠CAE=15°，AD=4，求AB的长．

7．如图，A、B、C在同一直线上，且△ABD，△BCE都是等边三角形，AE交BD于点M，CD交BE于点N，MN∥AC，求证：

（1）∠BDN=∠BAM；

（2）△BMN是等边三角形．

8．如图，若和都是等边三角形，求的度数．

9．如图，在△ABC中，AB＝BC，∠ABC＝120°，点D在边AC上，且线段BD绕着点B按逆时针方向旋转120°能与BE重合，点F是ED与AB的交点．

（1）求证：AE＝CD；

（2）若∠DBC＝45°，求∠BFE的度数．

10．如图，中，，中，，且，当把两个三角形如图①放置时，有．（不需证明）

（1）当把绕点旋转到图②③④的情况，其他条件不变，和还相等吗？请在图②③中选择一种情况进行证明；

（2）若图④中和交于点，连接，求证：平分．

11．如图，在等边三角形中，点在的延长线上，以为边在射线的右侧作等边三角形，连接，，求证：．

12．如图，以的边、向外作等边和等边，连接、．问：线段和有什么数量关系？试证明你的结论．

13．如图所示，和都是等边三角形，且在同一直线上，连结交于，连接交于，连结．

求证：（1）；

（2）；

（3）是等边三角形．

14．如图，点C是线段AB上任意一点（点C与点A，B不重合），分别以AC，BC为边在直线AB的同侧作等边三角形ACD和等边三角形BCE，AE与CD相交于点M，BD与CE相交于点N．连接MN．

证明：（1）△ACE≌△DCB；

（2）△ACM≌△DCN；

（3）MN∥AB．

15．图1、图2中，点C为线段AB上一点，△ACM与△CBN都是等边三角形．

（1）如图1，线段AN与线段BM是否相等？证明你的结论；

（2）线段AN与线段BM交于点O，求∠AOM的度数；

（3）如图2，AN与MC交于点E，BM与CN交于点F，探究△CEF的形状，并证明你的结论．

16．如图，∠1=∠2，AD=AE，∠B=∠ACE，且B、C、D三点在一条直线上．若∠B=60°，求证：CE=AC+CD．

17．如图，△ABD和△BCE都为等边三角形，连接AE、CD．求证：AE＝DC．

参考答案

1．C

【解析】

本题考查的是全等三角形的判定、等边三角形的性质以及旋转的性质的综合运用．根据等边三角形的三边相等、三个角都是60°，以及全等三角形的判定方法（SSS、SAS、ASA、AAS），进行证明．

解：△EBC≌△ACD，△GCE≌△FCD，△BCG≌△ACF．理由如下：

BC=AC，EC=CD，∠ACB=∠ECD，∠ACE是共同角⇒△EBC≌△ACD．

CD=EC，∠FCD=ECG，∠GEC=∠CDF⇒△GCE≌△FCD．

BC=AC，∠GBC=∠FAC，∠FCA=∠GCB⇒△BCG≌△ACF．

故选C．

2．D

【分析】

根据全等三角形的判定及角平分线的性质即可依次判断．

【详解】

∵DAB=CAE

∴DAB+BAC=CAE+BAC

∴DAC=EAB

∵AB=AD，AC=AE

∴△ADC≌△ABE

∴CD=BE，故①②正确；

∵△ADC≌△ABE

∴ADC =ABE

设AB与CD交于G点，

∵AGD =BGC

∴DOB=DAB=50°,故③正确；

过点A作AF⊥CD于F点，过点A作AH⊥BE于H点，

则AF、AH分别是△ADC与△ABE边上的高

∵△ADC≌△ABE

∴AF=AH

∴点A在DOE的平分线上，④正确

故选D．

【点拨】此题主要考查全等三角形的判定与性质，解题的关键是熟知角平分线的性质与判定．

3．①②④

【分析】

利用等边三角形的性质证明可判断①，利用，可得利用三角形的外角的性质可得 从而可判断③， 再结合等边三角形的性质证明可判断②， 由可得：，结合可得，从而可判断④．

【详解】

解：如图，记与的交点为，

∵与都是等边三角形，

∴AC=BC，CD=CE，∠BCA=∠DCE=60°

∵点B、C、E在同一条直线上，

∴∠ACD=60°，

∴∠BCD=∠ACE=120°

在和中，

∴，

所以结论①正确；

∵，

∴∠BDC=∠CEA，

∵∠AHB=∠DBE+∠BEA=∠DBE+∠BDC=180°∠BCD=60°， 所以③错误；

在和中，

，

∴，

∴所以②正确；

，

∵CG=CF，∠ACD=60°，

∴∠GFC=60，

又∵∠DCE=60°，

∴∠GFC=∠DCE，

∴GF∥BC，所以④正确．

故答案为：①②④．

【点拨】本题考查了全等三角形的判定和性质、等边三角形的性质和判定，平行线的判定，解决本题的关键是找到判定三角形全等的条件．

4．（1）见解析（2）90°

【分析】

（1）根据题意证明△ACE≌△BCD即可求解；

（2）根据三角形的内角和及全等三角形的性质即可得到的度数．

【详解】

（1）∵，，

∴∠ACB=∠ECD=90°

∴∠ACB+∠BCE=∠ECD+∠BCE

即∠ACE=∠BCD

又．

∴△ACE≌△BCD

∴

（2）∵△ACE≌△BCD

∴∠A=∠B

设AE与BC交于O点,

∴∠AOC=∠BOF

∴∠A+∠AOC+∠ACO=∠B+∠BOF+∠BFO=180°

∴∠BFO=∠ACO=90°

故=180°-∠BFO=90°．

【点拨】此题主要考查全等三角形的判定与性质，解题的关键是熟知全等三角形的判定定理．

5．（1）；（2），理由见解析

【分析】

（1）根据题意证明，根据三角形的内角和即可求解；

（2）设AD与CE交于F点，根据题意证明，根据平角的性质即可求解．

【详解】

（1）．理由如下：

，

．

，，

，

，

∴=

∵

∴;

（2）．理由如下：

设AD与CE交于F点．

，．

，，

，．

，．

，，

．

【点拨】此题主要考查全等三角形的判定与性质，解题的关键是熟知全等三角形的判定定理．

6．（1）见解析；（2）8

【分析】

（1）直接证明，即可得出结论；

（2）由（1）可进一步推出为直角三角形，且，从而由求解即可．

【详解】

（1）△ACB和△DCE均为等腰三角形，∠ACB=∠DCE=90°，

,

在与中，

，

；

（2）是等腰直角三角形，

，

由（1）可知，，,

，

，

则在中，，

．

【点拨】本题考查全等三角形的判定与性质，及含角的直角三角形的性质，根据“手拉手”模型证明全等，并推导出直角三角形是解题关键．

7．（1）证明过程见详解；（2）证明过程见详解。

【分析】

（1）只需要证明≌，就可以得到．

（2），因为MN∥AC，所以，,所以是等边三角形．

【详解】

证明：（1）∵

∴ 

在、中

∴≌

∴∠BDN=∠BAM

（2）∵，MN∥AC，

∴，

,

所以是等边三角形．

【点拨】这是一个典型的手拉手模型，是初中几何必会的模型之一，两个的三角形是等边三角形．

8．120°．

【分析】

利用等边三角形的性质可得AD＝AB，AC＝AE，∠DAB＝∠CAE＝60°，利用SAS即可证明△DAC≌△BAE，从而得出∠ABE＝∠ADC，设AB与CD交于点F，根据三角形内角和定理和等量代换即可求出∠BOF，利用平角的定义即可求出结论．

【详解】

证明：∵△ABD、△AEC都是等边三角形，

∴AD＝AB，AC＝AE，∠DAB＝∠CAE＝60°，

∵∠DAC＝∠BAC＋60°，∠BAE＝∠BAC＋60°，

∴∠DAC＝∠BAE，

在△DAC和△BAE中，

，

∴△DAC≌△BAE（SAS），

∴∠ABE＝∠ADC

设AB与CD交于点F，

∵∠BFO=∠DFA

∴∠BOF=180°－∠ABE－∠BFO=180°－∠ADC－∠DFA=∠DAB=60°

∴∠BOC=180°－∠BOF=120°．

【点拨】此题考查的是等边三角形的性质和全等三角形的判定及性质，利用SAS证出△DAC≌△BAE是解题关键．

9．（1）证明见解析；（2）∠BFE＝105°．

【分析】

（1）根据旋转的性质证明△ABE≌△CBD（SAS），进而得证；
 （2）由（1）得出∠DBC=∠ABE=45°，BD=BE，∠EBD=120°，最后根据三角形内角和定理进行求解即可．

【详解】

（1）证明：∵线段BD绕着点B按逆时针方向旋转120°能与BE重合，

∴BD＝BE，∠EBD＝120°，

∵AB＝BC，∠ABC＝120°，

∴∠ABD+∠DBC＝∠ABD+∠ABE＝120°，

∴∠DBC＝∠ABE，

∴△ABE≌△CBD（SAS），

∴AE＝CD；

（2）解：由（1）知∠DBC＝∠ABE＝45°，BD＝BE，∠EBD＝120°，

∴∠BED＝∠BDE＝（180°﹣120°）＝30°，

∴∠BFE＝180°﹣∠BED﹣∠ABE

＝180°﹣30°﹣45°＝105°．

【点拨】本题考查了旋转的性质，全等三角形的判定与性质，三角形内角和定理，利用旋转的性质证明是解题的关键．

10．（1）相等，证明见解析；（2）证明见解析

【分析】

（1）利用SAS证出△DCA≌△ECB，即可证出结论；

（2）过点C作CM⊥AD于M，CN⊥BE于N，利用SAS证出△DCA≌△ECB，从而得出CM=CN，然后利用角平分线的判定定理即可证出结论．

【详解】

解：（1）相等，证明图②如下

∵

∴

∴

在△DCA和△ECB中

∴△DCA≌△ECB

∴；

（2）过点C作CM⊥AD于M，CN⊥BE于N

∵

∴

∴

在△DCA和△ECB中

∴△DCA≌△ECB

∴CM=CN

∵CM⊥AD，CN⊥BE

∴平分

【点拨】此题考查的是全等三角形的判定及性质和角平分线的判定，掌握全等三角形的判定及性质和角平分线的判定是解题关键．

11．见解析

【分析】

根据△PAD和△ABC是等边三角形得到∠PAC=∠DAB，进而得到△PAC≌△DAB（SAS），即可求得结果．

【详解】

证明：∵△PAD和△ABC是等边三角形，

∴AP=AD，AC=AB，∠PAD=∠BAC=60°．

∴∠PAD+∠CAD=∠BAC+∠CAD，即∠PAC=∠DAB．

∴△PAC≌△DAB（SAS）．

∴CP=BD．

【点拨】本题主要考查了全等三角形的判定，准确利用等边三角形的性质是解题的关键．

12．，理由见解析．

【分析】

由和都是等边三角形，利用等边三角形的性质得到，，，利用等式的性质得到夹角相等，再用证明和全等，最后利用全等三角形对应边相等即可得证．

【详解】

解：，理由如下：

是等边三角形，

，，

是等边三角形，

，，

，

即，

在和中

，

≌，

．

【点拨】本题考查了全等三角形的判定和性质，根据等边三角形的性质得出夹角相等是解题的关键．

13．（1）见解析；（2）见解析；（3）见解析

【分析】

（1）由已知条件利用SAS证明△ABD≌△ACE即可．

（2）由已知条件利用ASA证明△ABM≌△ACN．

（3）根据得到，再根据即可证明．

【详解】

证明：和是等边三角形

即

在和中

由知

又

由可证

在和

由知

又知

是等边三角形．

【点拨】本题考查了全等三角形的判定与性质及等边三角形的性质；能够熟练掌握等边三角形的性质并利用性质证明三角形全等是正确解答本题的关键．

14．（1）见解析（2）见解析（3）见解析

【分析】

（1）由等边三角形的性质得出AC＝CD，BC＝CE，∠ACD＝∠BCE＝60°，得出∠DCB＝∠ACE，由SAS即可得出△ACE≌△DCB；

（2）由全等三角形的性质得出∠EAC＝∠BDC，再证出∠ACD＝∠DCE，由ASA证明△ACM≌△DCN即可；

（3）由全等三角形的性质得出CM＝CN，证出△MCN是等边三角形，得出∠MNC＝∠NCB＝60°，即可得出结论．

【详解】

（1）∵△ACD和△BCE是等边三角形，

∴AC＝CD，BC＝CE，∠ACD＝∠BCE＝60°，

∴∠ACD＋∠DCE＝∠BCE＋∠DCE，∠DCB＝∠ACE，

在△ACE与△DCB中，

，

∴△ACE≌△DCB（SAS）；

（2）由（1）得：△ACE≌△DCB，

∴∠EAC＝∠BDC，

∵∠ACD＝∠BCE＝60°，

∴∠DCE＝60°，

∴∠ACD＝∠DCE，

在△ACM与△DCN中，

，

∴△ACM≌△DCN（ASA）．

（3）由（2）得：△ACM≌△DCN，

∴CM＝CN，

又∵∠MCN＝180°−60°−60°＝60°，

∴△MCN是等边三角形，

∴∠MNC＝60°＝∠NCB，

∴MN∥AB．

【点拨】本题考查了等边三角形的性质、全等三角形的判定与性质、平行线的判定；熟练掌握等边三角形的性质，证明三角形全等是解决问题的关键．

15．（1）AN＝BM，见解析；（2）60°；（3）等边三角形，见解析

【分析】

（1）证△ACN≌△MCB（SAS），即可得出AN＝BM；

（2）由全等三角形的性质得∠ANC＝∠MBC，则∠AOM＝∠CAN+∠MBC＝∠CAN+∠ANC＝∠BCN＝60°；

（3）证△ACE≌△MCF（ASA），得CE＝CF，即可得出结论．

【详解】

解：（1）AN＝BM，理由如下：

∵△ACM、△CBN都是等边三角形，

∴AC＝CM，CN＝CB，∠ACM＝∠BCN＝60°，

∴∠ACM+∠MCN＝∠BCN+∠MCN，

∴∠ACN＝∠BCM，

在△ACN和△MCB中，

，

∴△ACN≌△MCB（SAS），

∴AN＝BM；

（2）由（1）得：△ACN≌△MCB，

∴∠ANC＝∠MBC，

∴∠AOM＝∠CAN+∠MBC＝∠CAN+∠ANC＝∠BCN＝60°；

（3）△CEF是等边三角形，理由如下：

∵△ACN≌△MCB，

∴∠CAE＝∠CMF，

∵∠MCF＝180°﹣∠ACM﹣∠BCN＝60°，

∴∠ACE＝∠MCF，

在△ACE和△MCF中，

，

∴△ACE≌△MCF（ASA），

∴CE＝CF，

∵∠MCF＝60°，

∴△CEF是等边三角形．

【点拨】本题考查等边三角形的性质、全等三角形的判定与性质，是重要考点，难度较易，掌握相关知识是解题关键．

16．证明见解析

【分析】

利用AAS证出△BAD≌△CAE，从而得出AB=AC，CE=BD=BC＋CD，根据等边三角形的判定定理可证△ABC为等边三角形，从而得出BC=AC，利用等量代换即可证出结论．

【详解】

证明：∵∠1=∠2

∴∠1＋∠CAD=∠2＋∠CAD

∴∠BAD=∠CAE

在△BAD和△CAE中

∴△BAD≌△CAE

∴AB=AC，CE=BD=BC＋CD

∵∠B=60°，

∴△ABC为等边三角形

∴BC=AC

∴CE=AC+CD．

【点拨】此题考查的是全等三角形的判定及性质和等边三角形的判定及性质，掌握全等三角形的判定及性质和等边三角形的判定及性质是解题关键．

17．见解析

【分析】

先由△ABD和△BCE是等边三角形，可知AB=BD，BE=BC，∠ABD=∠CBE，从而得到∠ABE=∠CBD，即可证明△ABE≌△DBC，从而得到结论．

【详解】

解：证明：∵△ABD和△BCE都为等边三角形，

∴AB=BD，BE=BC，∠ABD=∠CBE，

∴∠ABE=∠CBD，

∴△ABE≌△DBC（SAS），

∴AE=DC．

【点拨】本题考查的是等边三角形的性质及全等三角形的判定与性质，根据题意判断出△ABE≌△DBC是解答此题的关键．