2020-2021学年浙江省衢州市衢江区九年级（上）期末数学试卷

2020-2021学年浙江省衢州市衢江区九年级（上）期末数学试卷

一．选择题（本题有10小题，每小题3分，共30分。请在答题纸上将符合题意的正确选项涂黑，不选、多选、错选均不给分）

1．（3分）如图，把太阳与地平线分别抽象成圆和直线，则该图所呈现的直线与圆之间的位置关系是　　

A．相切 B．相交 C．相离 D．相似

2．（3分）一个不透明的布袋中装有1个白球和2个红球，它们除颜色不同以外其他都相同，从布袋中任意摸出一个球是白球的概率为　　

A． B． C． D．1

3．（3分）抛物线的对称轴是　　

A．直线 B．直线 C．直线 D．直线

4．（3分）如图，在半圆中，若，则的度数为　　

A． B． C． D．

5．（3分）已知，则的值是　　

A． B． C．2 D．

6．（3分）如图，在中，，若，，则的长为　　

A． B． C． D．

7．（3分）如图，、分别切于点、，且，切于点，交、于、两点，则的周长为　　

A．32 B．24 C．16 D．8

8．（3分）如图，取一张长为，宽为的矩形纸片，将它对折两次后得到一张小矩形纸片，若要使小矩形与原矩形相似，则原矩形纸片的边、应满足的条件是　　

A． B． C． D．

9．（3分）如图，将放在每个小正方形边长为1的网格中，点、、均落在格点上，用一个圆面去覆盖，能够完全覆盖这个三角形的最小圆面半径是　　

A． B． C．2 D．

10．（3分）汽车在刹车后，由于惯性作用还要继续向前滑行一段距离才能停下，我们称这段距离为“刹车距离”，刹车距离往往跟行驶速度有关，在一个限速的弯道上，甲、乙两辆汽车相向而行，发现情况不妙，同时刹车，最后还是相撞了事发后，交警现场测得甲车的刹车距离略超过，乙车的刹车距离略超过，又知甲、乙两种车型的刹车距离与车速的关系大致如下：，．由此可以推测　　

A．甲车超速 B．乙车超速 C．两车都超速 D．两车都未超速

二、填空题（本题有6小题，每小题4分，共24分）

11．（4分）2和8的比例中项是　 　．

12．（4分）在创建全国文明城市活动中，衢州市园林部门为了扩大市区的绿化面积，进行了大量的树木移栽．如表记录的是在相同条件下移栽某种幼树的棵数和成活棵数：

请根据表中数据估计，现园林部门移栽50000棵这种幼树，大约能成活 　　棵．

13．（4分）如图，是外一点，过引的切线、，若，则　　度．

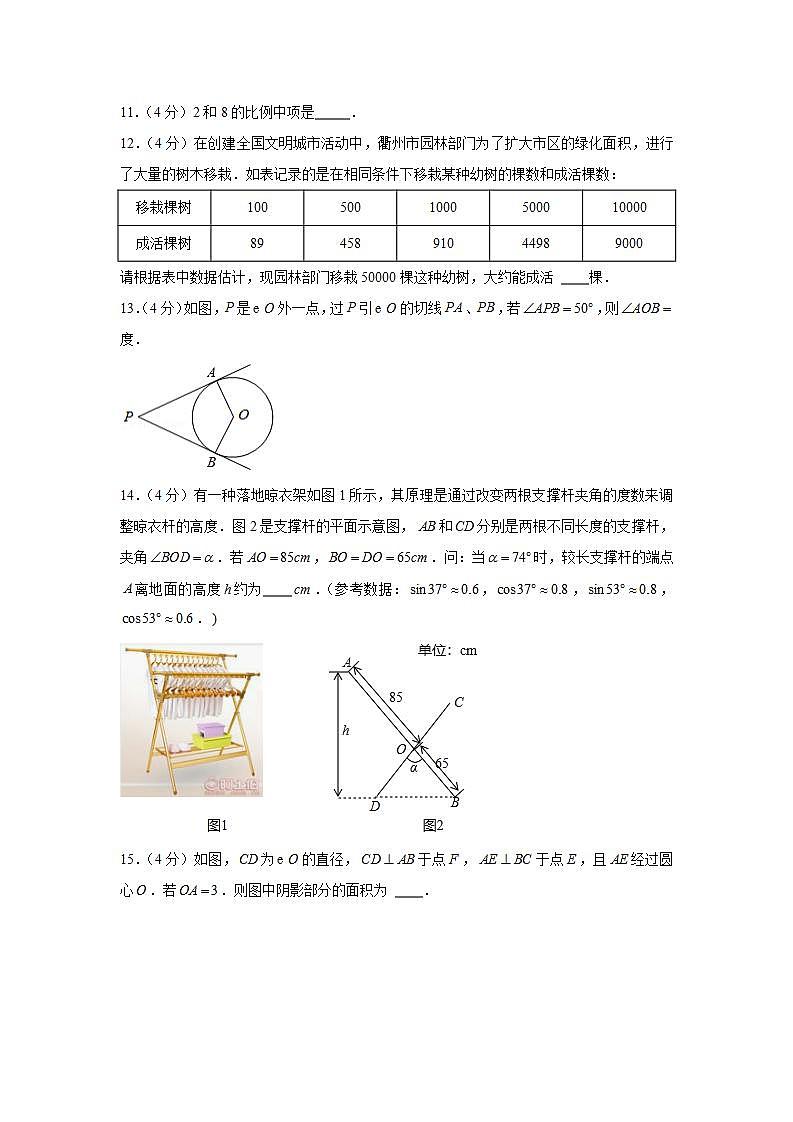
14．（4分）有一种落地晾衣架如图1所示，其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度．图2是支撑杆的平面示意图，和分别是两根不同长度的支撑杆，夹角．若，．问：当时，较长支撑杆的端点离地面的高度约为　　．（参考数据：，，，．

15．（4分）如图，为的直径，于点，于点，且经过圆心．若．则图中阴影部分的面积为 　　．

16．（4分）定义：若抛物线与轴有两个交点，且这两个交点与它的顶点所构成的三角形是直角三角形，则把这种抛物线称作“和美抛物线”．如图，一组抛物线的顶点，，，，为正整数）依次是直线上的点，这组抛物线与轴正半轴的交点依次是，，，，，，，，为正整数）．若这组抛物线中存在和美抛物线，则　　．

三、解答题（本题有8小题，共66分。请在答题纸的相应位置写出解题过程

17．（6分）计算：．

18．（6分）为巩固防疫成果，确保校园平安，全市所有学校都严格落实测体温进校园的防控要求．某校开设了、、三个测温通道，某天早晨，该校小亮和小丽两位同学将随机通过测温通道进入校园．

（1）小亮从测温通道通过的概率是 　　；

（2）利用画树状图或列表的方法，求小亮和小丽从同一个测温通道通过的概率．

19．（6分）如图，直线与相切于点，交于点，连结．已知，求的长．

20．（8分）如图，已知抛物线经过点，．

（1）求该抛物线的函数表达式；

（2）将抛物线向左平移1个单位，再向上平移4个单位得到一条新的抛物线，设新抛物线的顶点为，点在轴上，以为对角线的正方形的顶点、恰好都在新抛物线上，试求的值．

21．（8分）某超市销售一款“免洗洗手液”，这款“免洗洗手液”的成本价为每瓶16元，经试销发现，该种洗手液每天的销售单价与销售量的对应关系如表所示：

根据表中数据，解答下列问题：

（1）从表中可以发现，该洗手液的销售单价每增加1元，销售量减少 　　瓶；

（2）当销售单价为多少元时，才能使当天销售这款“免洗洗手液”的利润最大，最大利润为多少元？

22．（10分）阅读材料：关于三角函数有如下的公式：，．利用这些公式可以将两角和的三角函数值转化成两个三角函数值的和（差，如．

问题解决：根据以上阅读材料，请选择适当的公式解答下列问题．

（1）求；

（2）如图，边长为2的正沿直线滚动，设当滚动时，点的位置在，当滚动时，点的位置在．

①求的值；

②试确定的度数．

23．（10分）如图①，在矩形中，，，点、分别在边、上，且．

（1）当，时，求证：；

（2）当时，用直尺和圆规在图②的线段上确定所有使与以点、、为顶点的三角形相似的点（请保留画图痕迹）；

（3）探究：对于每一个确定的的值，线段上存在几个点，使得与以点、、为顶点的三角形相似？（直接写出结论即可）

24．（12分）李老师在上课时的屏幕上有如下内容：

如图，是的直径，点为弧的中点，连结交于点，，，老师要求同学们在矩形方框中添加一个条件和结论后，编制成一道完整的题目，并解答．

（1）李老师在方框中添加的内容是“，求的长”，请你解答；

（2）以下是小童和小诗的对话：

小童：我加的内容是“，连结，求的长”．

小诗：我加的内容是“，连结，求的值”．

请你帮小诗完成解答：

（3）参考第（1）题中李老师添加的内容及第（2）题中的对话，写出你想添加的内容（可以添线添字母，但所添内容不能与（1）、（2）中的内容相同），编制成一道完整的题目，并解答．

2020-2021学年浙江省衢州市衢江区九年级（上）期末数学试卷

参考答案与试题解析

一．选择题（本题有10小题，每小题3分，共30分。请在答题纸上将符合题意的正确选项涂黑，不选、多选、错选均不给分）

1．（3分）如图，把太阳与地平线分别抽象成圆和直线，则该图所呈现的直线与圆之间的位置关系是　　

A．相切 B．相交 C．相离 D．相似

【解答】解：太阳与地平线没有公共点，

该图所呈现的直线与圆之间的位置关系是相离．

故选：．

2．（3分）一个不透明的布袋中装有1个白球和2个红球，它们除颜色不同以外其他都相同，从布袋中任意摸出一个球是白球的概率为　　

A． B． C． D．1

【解答】解：一共有3个球，其中白球有1个，

因此摸出一球是白球的概率为，

故选：．

3．（3分）抛物线的对称轴是　　

A．直线 B．直线 C．直线 D．直线

【解答】解：

，

对称轴为直线，

故选：．

4．（3分）如图，在半圆中，若，则的度数为　　

A． B． C． D．

【解答】解：、、、四点共圆，

，

，

，

故选：．

5．（3分）已知，则的值是　　

A． B． C．2 D．

【解答】解：，

，

．

故选：．

6．（3分）如图，在中，，若，，则的长为　　

A． B． C． D．

【解答】解：，

，，

，

，

，，

，

，

解得．

故选：．

7．（3分）如图，、分别切于点、，且，切于点，交、于、两点，则的周长为　　

A．32 B．24 C．16 D．8

【解答】解：、分别切于点、，

，

切于点，

，，

的周长．

故选：．

8．（3分）如图，取一张长为，宽为的矩形纸片，将它对折两次后得到一张小矩形纸片，若要使小矩形与原矩形相似，则原矩形纸片的边、应满足的条件是　　

A． B． C． D．

【解答】解：小矩形与原矩形相似，原矩形纸片的边长为、，

，

，

，

（负数舍去），

故选：．

9．（3分）如图，将放在每个小正方形边长为1的网格中，点、、均落在格点上，用一个圆面去覆盖，能够完全覆盖这个三角形的最小圆面半径是　　

A． B． C．2 D．

【解答】解：如图所示：点为外接圆圆心，则为外接圆半径，

故能够完全覆盖这个三角形的最小圆面的半径是：．

故选：．

10．（3分）汽车在刹车后，由于惯性作用还要继续向前滑行一段距离才能停下，我们称这段距离为“刹车距离”，刹车距离往往跟行驶速度有关，在一个限速的弯道上，甲、乙两辆汽车相向而行，发现情况不妙，同时刹车，最后还是相撞了事发后，交警现场测得甲车的刹车距离略超过，乙车的刹车距离略超过，又知甲、乙两种车型的刹车距离与车速的关系大致如下：，．由此可以推测　　

A．甲车超速 B．乙车超速 C．两车都超速 D．两车都未超速

【解答】解甲车的刹车距离为，

，

即，

解得：（不合题意舍去），

所以甲车的速度为，不超过限速，

而乙车的刹车距离为，

则有，

即，

解得：，（不合题意舍去），

所以乙车的速度为，超过了限速的规定．

故选：．

二、填空题（本题有6小题，每小题4分，共24分）

11．（4分）2和8的比例中项是　　．

【解答】解：设其比例中项是，

，

．

故答案为．

12．（4分）在创建全国文明城市活动中，衢州市园林部门为了扩大市区的绿化面积，进行了大量的树木移栽．如表记录的是在相同条件下移栽某种幼树的棵数和成活棵数：

请根据表中数据估计，现园林部门移栽50000棵这种幼树，大约能成活 　4500　棵．

【解答】解：设能成活棵，根据题意得：

，

解得：．

故大约能成活4500棵．

故答案为：4500．

13．（4分）如图，是外一点，过引的切线、，若，则　130　度．

【解答】解：、是的切线，

，

，

，

故答案为：130．

14．（4分）有一种落地晾衣架如图1所示，其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度．图2是支撑杆的平面示意图，和分别是两根不同长度的支撑杆，夹角．若，．问：当时，较长支撑杆的端点离地面的高度约为　120　．（参考数据：，，，．

【解答】解：过作，过作，可得，

，

平分，

，

，

在中，，

，

故答案为：120

15．（4分）如图，为的直径，于点，于点，且经过圆心．若．则图中阴影部分的面积为 　　．

【解答】解：连接，

于点，于点，

，

，

，

，

，，

，

，

，，

，

，

，

，

，

，

图中阴影部分的面积，

故答案为：．

16．（4分）定义：若抛物线与轴有两个交点，且这两个交点与它的顶点所构成的三角形是直角三角形，则把这种抛物线称作“和美抛物线”．如图，一组抛物线的顶点，，，，为正整数）依次是直线上的点，这组抛物线与轴正半轴的交点依次是，，，，，，，，为正整数）．若这组抛物线中存在和美抛物线，则　或　．

【解答】解：直线经过点则，

直线，

由抛物线的对称性知：抛物线的顶点与轴的两个交点构成的直角三角形必为等腰直角三角形；

该等腰三角形的高等于斜边的一半

该等腰直角三角形的斜边长小于2，斜边上的高小于1（即抛物线的顶点纵坐标小于

当时，，

当时，，

当时，；

美丽抛物线的顶点只有、

①若为顶点，由，，则

②若为顶点，由，则综上所述，的值为或时，存在美丽抛物线．

故答案为：或．

三、解答题（本题有8小题，共66分。请在答题纸的相应位置写出解题过程

17．（6分）计算：．

【解答】解：原式

．

18．（6分）为巩固防疫成果，确保校园平安，全市所有学校都严格落实测体温进校园的防控要求．某校开设了、、三个测温通道，某天早晨，该校小亮和小丽两位同学将随机通过测温通道进入校园．

（1）小亮从测温通道通过的概率是 　　；

（2）利用画树状图或列表的方法，求小亮和小丽从同一个测温通道通过的概率．

【解答】解：（1）小亮从测温通道通过的概率是，

故答案为：；

（2）列表如下：

由表可知，共有9种等可能的结果，其中小明和小丽从同一个测温通道通过的有3种可能，

所以小亮和小丽从同一个测温通道通过的概率为．

19．（6分）如图，直线与相切于点，交于点，连结．已知，求的长．

【解答】解：连接，

直线与相切于点，

，

，，

是等边三角形，

，，

．

20．（8分）如图，已知抛物线经过点，．

（1）求该抛物线的函数表达式；

（2）将抛物线向左平移1个单位，再向上平移4个单位得到一条新的抛物线，设新抛物线的顶点为，点在轴上，以为对角线的正方形的顶点、恰好都在新抛物线上，试求的值．

【解答】解：（1）抛物线经过点，．

，

解得，

抛物线的解析式为；

（2），

将抛物线向左平移1个单位，再向上平移4个单位得到，即，

，

点在轴上，以为对角线的正方形的顶点、恰好都在新抛物线上，

，轴，且、关于轴对称，

，，，，

，

解得，（舍去），

的值为2．

21．（8分）某超市销售一款“免洗洗手液”，这款“免洗洗手液”的成本价为每瓶16元，经试销发现，该种洗手液每天的销售单价与销售量的对应关系如表所示：

根据表中数据，解答下列问题：

（1）从表中可以发现，该洗手液的销售单价每增加1元，销售量减少 　20　瓶；

（2）当销售单价为多少元时，才能使当天销售这款“免洗洗手液”的利润最大，最大利润为多少元？

【解答】解：（1）该洗手液的销售单价每增加1元，销售量减少20瓶，

故答案为：20；

（2）设每天的销售利润为元，则有：

，

，

二次函数图象开口向下，

当时，有最大值，最大值为500元．

答：当销售单价为21元时，销售这款“免洗洗手液”每天的销售利润最大，最大利润为500元．

22．（10分）阅读材料：关于三角函数有如下的公式：，．利用这些公式可以将两角和的三角函数值转化成两个三角函数值的和（差，如．

问题解决：根据以上阅读材料，请选择适当的公式解答下列问题．

（1）求；

（2）如图，边长为2的正沿直线滚动，设当滚动时，点的位置在，当滚动时，点的位置在．

①求的值；

②试确定的度数．

【解答】解：（1）

；

（2）①过作于，

是等边三角形且边长为2，

，，

；

②过作于，

是等边三角形且边长为2，

，，

．

设，，

，

，

．

23．（10分）如图①，在矩形中，，，点、分别在边、上，且．

（1）当，时，求证：；

（2）当时，用直尺和圆规在图②的线段上确定所有使与以点、、为顶点的三角形相似的点（请保留画图痕迹）；

（3）探究：对于每一个确定的的值，线段上存在几个点，使得与以点、、为顶点的三角形相似？（直接写出结论即可）

【解答】（1）证明：如图①中，

四边形是矩形，

，

，，，，

，，

，，

，都是等腰直角三角形，

．

（2）解：时，线段上与的相似点有3个，理由如下：

延长，作点关于的对称点，连接，交于点；连接，以为直径作圆交于点、，如图：

点关于的对称点，

△，

，

△，

，即是线段上与的相似点，

是的直径，

，

，

又，

△，即是线段上与的相似点，

同理可证是线段上与的相似点，

综上所述，线段上与的相似点有3个；

（3）解：当且时，线段上与的相似点有3个；

当时，线段上与的相似点有2个；

当时，线段上与的相似点有2个；

当时，线段上与的相似点有1个．

24．（12分）李老师在上课时的屏幕上有如下内容：

如图，是的直径，点为弧的中点，连结交于点，，，老师要求同学们在矩形方框中添加一个条件和结论后，编制成一道完整的题目，并解答．

（1）李老师在方框中添加的内容是“，求的长”，请你解答；

（2）以下是小童和小诗的对话：

小童：我加的内容是“，连结，求的长”．

小诗：我加的内容是“，连结，求的值”．

请你帮小诗完成解答：

（3）参考第（1）题中李老师添加的内容及第（2）题中的对话，写出你想添加的内容（可以添线添字母，但所添内容不能与（1）、（2）中的内容相同），编制成一道完整的题目，并解答．

【解答】解：（1）点为弧的中点，

，

，

，

，

，

是的直径，

，

，

；

（2）如图，连接交于点，

点为弧的中点，

，，

，

，

，

，

由（1）知，，，

，

，

，

；

（3）连接交于点，若，求的长．

，，

，

，

，

．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布

日期：2021/12/2 14:29:17；用户：初中数学2；邮箱：jse033@xyh.com；学号：39024123