

北师大新版2020-2021学年九年级上册数学期末复习试题(Word版 含解析)
展开北师大新版2020-2021学年九年级上册数学期末复习试题
一.选择题(共12小题,满分48分,每小题4分)
1.下列方程中,一元二次方程共有( )
①3x2+x=20 ②2x2﹣3xy+4=0 ③x3﹣x=1 ④x2=1
A.1个 B.2个 C.3个 D.4个
2.如图所示几何体的左视图正确的是( )
A. B. C. D.
3.若,则的值为( )
A.1 B. C. D.
4.如果点A(﹣5,y1),B(﹣,y2),C(,y3)在双曲线y=上(k<0),则y1,y2,y3的大小关系是( )
A.y3<y1<y2 B.y2<y1<y3 C.y1<y2<y3 D.y1<y3<y2
5.在Rt△ABC中,AC=8,BC=6,则cosA的值等于( )
A. B. C.或 D.或
6.将抛物线( )先向下平移1个单位长度,再向左平移2个单位长度后所得到的抛物线为y=﹣2(x﹣3)2+1.
A.y=﹣2(x﹣5)2+2 B.y=﹣2(x﹣1)2
C.y=﹣2(x﹣2)2﹣1 D.y=﹣2(x﹣4)2+3
7.反比例函数y=(m为常数),在每个象限内,y随x的增大而减小,则m取值范围是( )
A.m>0 B.m>2 C.m<0 D.m<2
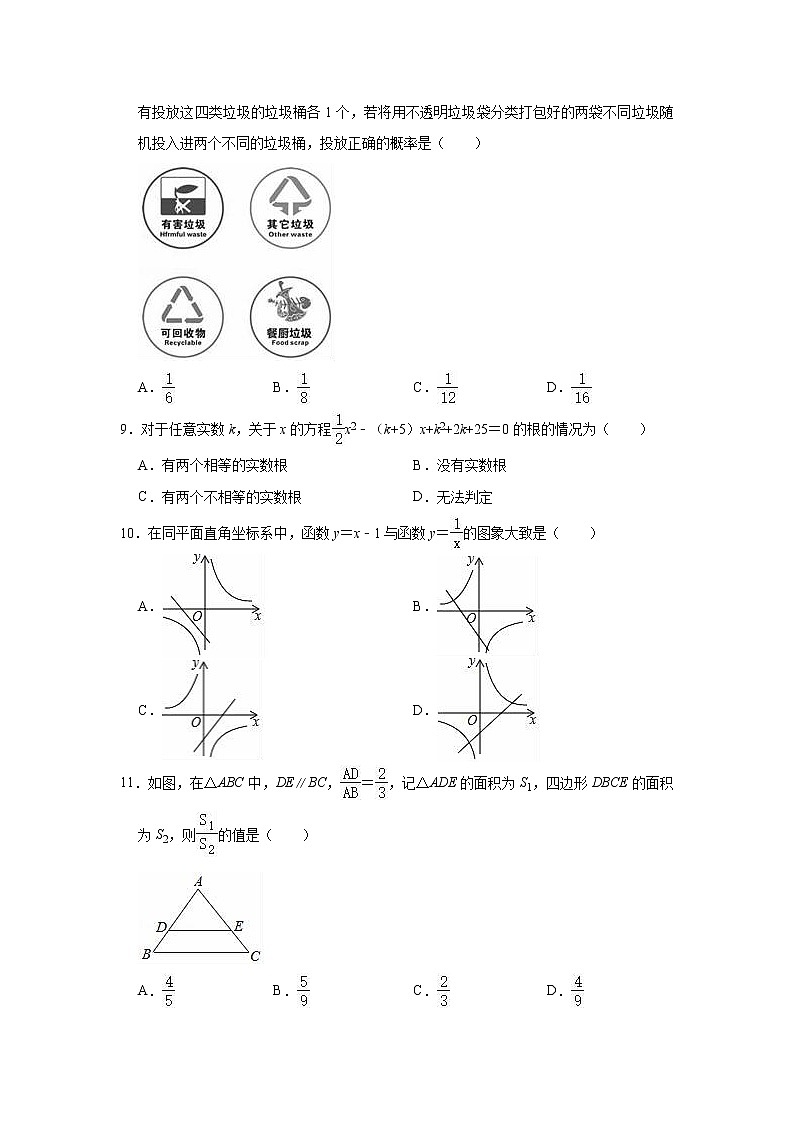
8.太原是我国生活垃圾分类的46个试点城市之一,垃圾分类的强制实施也即将提上日程.根据规定,我市将垃圾分为了四类:可回收垃圾、餐厨垃圾、有害垃圾和其他垃圾.现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投入进两个不同的垃圾桶,投放正确的概率是( )
A. B. C. D.
9.对于任意实数k,关于x的方程x2﹣(k+5)x+k2+2k+25=0的根的情况为( )
A.有两个相等的实数根 B.没有实数根
C.有两个不相等的实数根 D.无法判定
10.在同平面直角坐标系中,函数y=x﹣1与函数y=的图象大致是( )
A. B.
C. D.
11.如图,在△ABC中,DE∥BC,=,记△ADE的面积为S1,四边形DBCE的面积为S2,则的值是( )
A. B. C. D.
12.关于x的二次函数+,其中a为锐角,则:
①当a为30°时,函数有最小值﹣;
②函数图象与坐标轴可能有三个交点,并且当a为45°时,连接这三个交点所围成的三角形面积小于1;
③当a<60°时,函数在x>1时,y随x的增大而增大;
④无论锐角a怎么变化,函数图象必过定点.
其中正确的结论有( )
A.①② B.①②③ C.①②④ D.②③④
二.填空题(共6小题,满分24分,每小题4分)
13.2sin45°+2cos60°﹣tan60°= .
14.一个不透明的袋子中装有若干个红球和6个黄球,它们除颜色外都相同,从中随机摸出一个球,记下颜色后放回,通过大量反复实验发现,摸到黄球的频率约为0.3,由此推测从这个袋中摸到红球的概率约为 .
15.如图,直立在点B处的标杆AB=2.5m,站立在点F处的观测者从点E看到标杆顶A,树顶C在同一直线上(点F,B,D也在同一直线上).已知BD=10m,FB=3m,人的高度EF=1.7m,则树高DC是 .(精确到0.1m)
16.二次函数y=ax2+bx+c的图象如图,其图象与x轴的一个交点为(,0),则不等式ax2+bx+c≤0的解集为 .
17.如图,点A是双曲线y=﹣在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=上运动,则k的值为 .
18.已知点D(2,a)为直线y=﹣x+3上一点,将一直角三角板的直角顶点放在D处旋转,保持两直角边始终轴交于A、B两点,C(0,﹣1)为y轴上一点,连接AC,BC,则四边形ACBD面积的最小值为 .
三.解答题(共9小题,满分78分)
19.解方程:x2+x﹣2=0.
20.计算:﹣(3.14﹣π)0+(1﹣cos30°)×()﹣2.
21.如图,已知在四边形ABCD中,∠ABC=∠ADB=90°,AB=5,AD=3,BC=,CE⊥BD,求四边形ABCD的面积S四边形ABCD.
22.某数学社团成员想利用所学的知识测量某广告牌的宽度(图中线段MN的长),直线MN垂直于地面,垂足为点P.在地面A处测得点M的仰角为58°、点N的仰角为45°,在B处测得点M的仰角为31°,AB=5米,且A、B、P三点在一直线上.请根据以上数据求广告牌的宽MN的长.
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60,sin31°=0.52,cos31°=0.86,tan31°=0.60.)
23.如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发那么几秒后,PQ的长度等于cm?
(2)在(1)中,△PQB的面积能否等于7cm2?请说明理由.
24.图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字2,3,4,5.图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子在桌面掷出后,看骰子落在桌面上(即底面)的数字是几,就从图中的A点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法继续……
(1)随机掷一次骰子,则棋子跳动到点C处的概率是 .
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
25.已知点A在x轴负半轴上,点B在y轴正半轴上,线段OB的长是方程x2﹣2x﹣8=0的解,tan∠BAO=.
(1)求点A的坐标;
(2)点E在y轴负半轴上,直线EC⊥AB,交线段AB于点C,交x轴于点D,S△DOE=16.若反比例函数y=的图象经过点C,求k的值;
(3)在(2)条件下,点M是DO中点,点N,P,Q在直线BD或y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
26.如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
27.如图,已知抛物线C1:y=x2+bx+c与x轴交于A,B两点(点A在点B的左边),与y轴的负半轴交于点C,且OB=OC=3•OA.
(1)求抛物线的解析式;
(2)点P是抛物线C1上的一动点,设△PAC的面积为S1,△PBC的面积为S2,若>3,求点P的横坐标xP的取值范围;
(3)把抛物线C1向左平移1个单位长度,再向上平移4个单位长度得到抛物线C2,点E(1﹣m,2m﹣8)到C2上的某一点F的最小距离为d,直接写出C2上的点F的坐标及d的值.
参考答案与试题解析
一.选择题(共12小题,满分48分,每小题4分)
1.解:一元二次方程有:3x2+x=20,x2=1,共2个,
故选:B.
2.解:从几何体的左面看所得到的图形是:
故选:A.
3.解:∵,
∴=2=2﹣=;
故选:B.
4.解:当x=﹣5,y1==﹣,
当x=﹣,y2=﹣=﹣k,
当x=,y3=k=k,
而k<0,
所以y3<y1<y2.
故选:A.
5.解:当△ABC为直角三角形时,存在两种情况:
①当AB为斜边,∠C=90°,
∵AC=8,BC=6,
∴AB===10.
∴cosA===;
②当AC为斜边,∠B=90°,
由勾股定理得:AB===2,
∴cosA==;
综上所述,cosA的值等于或.
故选:C.
6.解:∵将y=﹣2(x﹣3)2+1,先向上平移1个单位长度,再向右平移2个单位长度得到y=﹣2(x﹣5)2+2,
∴平移前抛物线的解析式是:y=﹣2(x﹣5)2+2.
故选:A.
7.解:∵反比例函数y=(m为常数),在每个象限内,y随x的增大而减小,
∴m﹣2>0,
解得,m>2,
故选:B.
8.解:回收垃圾、厨余垃圾、有害垃圾和其他垃圾对应的垃圾筒分别用A,B,C,D表示,垃圾分别用a,b,c,d表示.设分类打包好的两袋不同垃圾为a、b,
画树状图如图:
共有12个等可能的结果,分类打包好的两袋不同垃圾随机投入进两个不同的垃圾桶,投放正确的结果有1个,
∴分类打包好的两袋不同垃圾随机投入进两个不同的垃圾桶,投放正确的概率为;
故选:C.
9.解: x2﹣(k+5)x+k2+2k+25=0,
△=b2﹣4ac=[﹣(k+5)]2﹣4××(k2+2k+25)=﹣k2+6k﹣25=﹣(k﹣3)2﹣16,
不论k为何值,﹣(k﹣3)2≤0,
即△=﹣(k﹣3)2﹣16<0,
所以方程没有实数根,
故选:B.
10.解:函数y=中k=1>0,故图象在第一、三象限;函数y=x﹣1的图象在第一、三、四象限,
故选:D.
11.解:∵DE∥BC,
∴△ADE∽△ABC,
∵=,
∴=,
∴=,
∴9S1=4S1+4S2,
∴5S1=4S2,
∴=.
故选:A.
12.解:①当a=30°时,sina=,二次函数解析式可写作:y=x2﹣x=(x﹣)2﹣;
所以当a为30°时,函数的最小值为﹣;故①正确.
②令y=0,则有:2sinax2﹣(4sina+)x﹣sina+=0,
△=(4sina+)2﹣4×2sina×(﹣sina+)=24sin2a+>0,
所以抛物线与x轴一定有两个交点,再加上抛物线与y轴的交点,即与坐标轴可能有三个交点(当图象过原点时,只有两个交点);
设抛物线与x轴的交点为(x1,0)、(x2,0);
当a=45°时,sina=,得:y=x2﹣(2+)x﹣,则:
三角形的面积 S=|x1﹣x2|×=×=×≈0.3<1
故②正确.
③∵2sina>0,且对称轴x=﹣=1+>1,
∴x=1在抛物线对称轴的左侧,因此 x>1时,y随x的增大先减小后增大;
故③错误.
④y=2sinax2﹣(4sina+)x﹣sina+=sina(2x2﹣4x﹣1)﹣x+;
当2x2﹣4x﹣1=0,即 x=1±时,抛物线经过定点,且坐标为:(1+,﹣)、(1﹣,);
故④正确.
综上,正确的选项是①②④,故选C.
二.填空题(共6小题,满分24分,每小题4分)
13.解:原式=2×+2×﹣×
=+1﹣3
=﹣2.
故答案为:﹣2.
14.解:∵袋子例只有红球和黄球,通过大量反复实验发现,摸到黄球的频率约为0.3,
∴摸到黄球的概率为0.3,
∴摸到红球的概率约为0.7,
故答案为:0.7.
15.解:过E作EH⊥CD交CD于H点,交AB于点G,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB
∴四边形EFDH为矩形
∴EF=GB=DH=1.7,EG=FB=3,GH=BD=10
∴AG=AB﹣GB=0.8
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH
∴=
∵EH=EG+GH=13
∴CH=≈3.5
∴CD=CH+HD=5.2
即树高DC为5.2米.
故答案为:5.2m.
16.解:∵二次函数y=ax2+bx+c的图象与x轴的一个交点为(,0),且其对称轴为x=﹣1
∴﹣(﹣1)=,﹣1﹣=﹣
∴抛物线与x轴的另一个交点坐标为(﹣,0)
∴结合函数图象可得,不等式ax2+bx+c≤0的解集为:x≤﹣或x≥.
故答案为:x≤﹣或x≥.
17.解:连接CO,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,
∵连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,
∴CO⊥AB,∠CAB=30°,
则∠AOD+∠COE=90°,
∵∠DAO+∠AOD=90°,
∴∠DAO=∠COE,
又∵∠ADO=∠CEO=90°,
∴△AOD∽△OCE,
∴===tan60°=,
∴=()2=3,
∵点A是双曲线y=﹣在第二象限分支上的一个动点,
∴S△AOD=×|xy|=,
∴S△EOC=,即×OE×CE=,
∴k=OE×CE=3,
故答案为:3.
18.解:如图,
取AB的中点F,连接DF,
∵∠ADB=90°,
∴AB=2DF
∵点D(2,a)为直线y=﹣x+3上一点,
∴a=﹣×2+3=2,
∴D(2,2),
过点D作DE⊥AB于E,
∴DE=2,E(2,0),
∴S四边形ACBD=S△ABC+S△ABD=AB•OC+AB•DE=AB(OC+DE)=AB=3DF,
要四边形ACBD的面积最小,即DF最小,
∵点D(2,2),点F在x轴上,
∴当DF⊥x轴时,DF最小,最小值为DE=2,
∴S四边形ACBD最小=3×2=6,
故答案为6.
三.解答题(共9小题,满分78分)
19.解:分解因式得:(x﹣1)(x+2)=0,
可得x﹣1=0或x+2=0,
解得:x1=1,x2=﹣2.
20.解:原式=﹣1+(1﹣)×4
=﹣1+4﹣2
=;
21.解:在Rt△ABD中,AB=5,AD=3,
∴BD===4,
∵∠ADB=∠CEB=90°,
∠ABD+∠CBD=90°,
∴∠CBD=∠BAD,
∴△ABD∽△BCE,
∴,
∴,
S四边形ABCD=S△ABD+S△BCD=AD×BD+BD×CE=+,
=6+5.
22.解:在Rt△APN中,∠NAP=45°,
∴PA=PN,
在Rt△APM中,tan∠MAP=,
设PA=PN=x,
∵∠MAP=58°,
∴MP=AP•tan∠MAP=1.6x,
在Rt△BPM中,tan∠MBP=,
∵∠MBP=31°,AB=5,
∴0.6=,
∴x=3,
∴MN=MP﹣NP=0.6x=1.8(米),
答:广告牌的宽MN的长为1.8米.
23.(1)设x秒后,PQ=2
BP=5﹣x BQ=2x
∵BP2+BQ2=PQ2
∴(5﹣x)2+(2x)2=(2)2
解得:x1=3,x2=﹣1(舍去)
∴3秒后,PQ的长度等于2;
(2)△PQB的面积不能等于7cm2,原因如下:
设t秒后,PB=5﹣t QB=2t
又∵S△PQB=×BP×QB=7
×(5﹣t)×2t=7
∴t2﹣5t+7=0
△=52﹣4×1×7=25﹣28=﹣3<0
∴方程没有实数根
∴△PQB的面积不能等于7cm2.
24.解:(1)随机掷一次骰子,则棋子跳动到点C处的概率是,
故答案为;
(2)列表如图:
共有16种可能,和为8可以到达点C,有3种情形,所以棋子最终跳动到点C处的概率为.
25.解:(1)∵线段OB的长是方程x2﹣2x﹣8=0的解,
∴OB=4,
在Rt△AOB中,tan∠BAO==,
∴OA=8,
∴A(﹣8,0).
(2)∵EC⊥AB,
∴∠ACD=∠AOB=∠DOE=90°,
∴∠OAB+∠ADC=90°,∠DEO+∠ODE=90°,
∵∠ADC=∠ODE,
∴∠OAB=∠DEO,
∴△AOB∽△EOD,
∴=,
∴OE:OD=OA:OB=2,设OD=m,则OE=2m,
∵•m•2m=16,
∴m=4或﹣4(舍弃),
∴D(﹣4,0),E(0,﹣8),
∴直线DE的解析式为y=﹣2x﹣8,
∵A(﹣8,0),B(0,4),
∴直线AB的解析式为y=x+4,
由,解得,
∴C(﹣,),
∵若反比例函数y=的图象经过点C,
∴k=﹣.
(3)如图1中,当四边形MNPQ是矩形时,∵OD=OB=4,
∴∠OBD=∠ODB=45°,
∴∠PNB=∠ONM=45°,
∴OM=DM=ON=2,
∴BN=2,PB=PN=,
∴P(﹣1,3).
如图2中,当四边形MNPQ是矩形时(点N与原点重合),易证△DMQ是等腰直角三角形,OP=MQ=DM=2,P(0,2);
如图3中,当四边形MNPQ是矩形时,设PM交BD于R,易知R(﹣1,3),可得P(0,6)
如图4中,当四边形MNPQ是矩形时,设PM交y轴于R,易知PR=MR,可得P(2,6).
综上所述,满足条件的点P坐标为(﹣1,3)或(0,2)或(0,6)或(2,6);
26.解:(1)∵四边形ABCD是正方形,
∴AB=CB=CD=DA=4,∠D=∠DAB=90°,∠DAC=∠BAC=45°,
∴AC==4,
∵∠DAC=∠AHC+∠ACH=45°,∠ACH+∠ACG=45°,
∴∠AHC=∠ACG.
故答案为=.
(2)结论:AC2=AG•AH.
理由:∵∠AHC=∠ACG,∠CAH=∠CAG=135°,
∴△AHC∽△ACG,
=,
∴AC2=AG•AH.
(3)①△AGH的面积不变.
理由:∵S△AGH=•AH•AG=AC2=×(4)2=16.
∴△AGH的面积为16.
②如图1中,当GC=GH时,易证△AHG≌△BGC,
可得AG=BC=4,AH=BG=8,
∵BC∥AH,
∴==,
∴AE=AB=.
如图2中,当CH=HG时,
易证AH=BC=4(可以证明△GAH≌△HDC得到)
∵BC∥AH,
∴==1,
∴AE=BE=2.
如图3中,当CG=CH时,易证∠ECB=∠DCF=22.5°.
在BC上取一点M,使得BM=BE,
∴∠BME=∠BEM=45°,
∵∠BME=∠MCE+∠MEC,
∴∠MCE=∠MEC=22.5°,
∴CM=EM,设BM=BE=x,则CM=EM=x,
∴x+x=4,
∴x=4(﹣1),
∴AE=4﹣4(﹣1)=8﹣4,
综上所述,满足条件的m的值为或2或8﹣4.
27.解:(1)设OA=n,则OB=OC=3n,
则A(﹣n,0),B(3n,0),C(0,﹣3n),
将A(﹣n,0),B(3n,0),C(0,﹣3n)代入y=x2+bx+c,
得,
解得,
∴A(﹣1,0),B(3,0),C(0,﹣3),抛物线的解析式为y=x2﹣2x﹣3;
(2)当时,设点P在抛物线上的P1处,
分别过A,B作直线P1C的垂线,垂足分别为G,H,直线P1C交x轴于M,
①如图1,当点A,B分别在直线P1C的异侧时,
∵∠AGM=∠BHM=90°,∠AMG=∠BMH,
∴△AGM∽△BHM,
则,
由(1)知,A(﹣1,0),B(3,0),
∴AB=4,
∴BM=1,OM=2,
∴M(2,0),
由(1)知,C(0,﹣3),
∴可设直线P1C的解析式为y=kx﹣3,
将点M(2,0)代入y=kx﹣3,
得,2k﹣3=0,
∴k=,
∴直线P1C:y=,
联立,
解得,x1=0(舍去),x2=,
∴点P1的横坐标为;
②如图2,当点A,B分别在直线P1C的同侧时,
∵∠AGM=∠BHM=90°,
∴BH∥AG,
∴△AGM∽△BHM,
则,
由(1)知,A(﹣1,0),B(3,0),
∴AB=4,
∴BM=2,OM=5,
∴M(5,0),
由(1)知,C(0,﹣3),
∴可设直线P1C的解析式为y=kx﹣3,
将点M(5,0)代入y=kx﹣3,
得,5k﹣3=0,
∴k=,
∴直线P1C:y=x﹣3,
联立,
解得,x1=0(舍去),x2=,
∴点P1的横坐标为;
∵,
∴由图象知:<xp<且xp≠3;
(3)∵抛物线C1的解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴将抛物线C1向左平移1个单位长度,再向上平移4个单位长度得到抛物线C2的解析式为y=x2,
∵点E(1﹣m,2m﹣8),
∴x=1﹣m,y=2m﹣8,
∴m=1﹣x,m=y+4,
∴1﹣x=y+4,
即y=﹣2x﹣6,
∴点E在直线y=﹣2x﹣6上运动,
设F(t,t2),过F作FQ∥y轴交直线y=﹣2x﹣6于Q,
则Q(t,﹣2t﹣6),
∴FQ=t2+2t+6,
过F作FG垂直直线y=﹣2x﹣6于G,
设直线y=﹣2x﹣6与x轴交于点E,与y轴交于点K,
则E(﹣3,0),K(0,﹣6),
在Rt△EOK中,EK==3,
∵∠EKO=∠FQG,∠EOK=∠FGQ=90°,
∴△EOK∽△FGQ,
∴=,
即=,
∴FG=,
由二次函数的图象及性质可知,当t=﹣1时,FG取最小值,
∴F(﹣1,1),d=.
2020-2021学年北师大新版九年级上册数学期末复习试卷(word解析版): 这是一份2020-2021学年北师大新版九年级上册数学期末复习试卷(word解析版),共23页。试卷主要包含了如图所示几何体的左视图正确的是,若,则的值为等内容,欢迎下载使用。
2020-2021学年北师大新版九年级上册数学期末复习试题1(Word版 含解析): 这是一份2020-2021学年北师大新版九年级上册数学期末复习试题1(Word版 含解析),共17页。试卷主要包含了下列计算正确的是,估算的值是在,计算﹣的结果是等内容,欢迎下载使用。
2020-2021学年北师大新版九年级上册数学期末复习试卷2(Word版 含解析): 这是一份2020-2021学年北师大新版九年级上册数学期末复习试卷2(Word版 含解析),共20页。试卷主要包含了对于二次函数y=2,把函数y=,小亮根据x的取值等内容,欢迎下载使用。












