

人教版数学八年级上册 最新人教版初二(八年级)数学上册各单元及期末测试题(含答案)
展开最新人教版八年级数学上册各单元及期末测试题(含答案)
人教版八年级数学上册第一单元测试
一、选择题(24分)
1.用尺规作已知角的平分线的理论依据是( )
A.SAS B.AAS C.SSS D.ASA
2.三角形中到三边距离相等的点是( )
A.三条边的垂直平分线的交点 B.三条高的交点
C.三条中线的交点 D.三条角平分线的交点
3. 已知△ABC≌△A´B´C´,且△ABC的周长为20,AB=8,BC=5,则A´C´等于( )
A. 5 B. 6 C. 7 D. 8
4.如图所示,在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )
D
E
A
F
B
C
A. 15° B. 20° C. 25° D. 30°
A
B
C
E
M
F
D
N
4题图 5题图 6题图
5.如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△CAN≌△ABM.其中正确的结论是( )
A.①③④ B.②③④ C.①②③ D.①②④
6.如图,△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,有下面四个结论:①DA平分∠EDF;②AE=AF;③AD上的点到B,C两点的距离相等;④到AE,AF的距离相等的点到DE,DF的距离也相等.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.已知AD是△ABC的角平分线,DE⊥AB于E,且DE=3cm,则点D到AC的距
离是( )
A.2cm B.3cm C.4cm D.6cm
8.下列说法:①角的内部任意一点到角的两边的距离相等;②到角的两边
距离相等的点在这个角的平分线上;③角的平分线上任意一点到角的两边
的距离相等;④△ABC中∠BAC的平分线上任意一点到三角形的三边的距离
相等,其中正确的( )
A.1个 B.2个 C.3个 D.4个
二、填空题(30分)
9.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28 cm2,AB=20cm,AC=8cm,则DE的长为_________ cm.
10. 已知△ABC≌△DEF,AB=DE,BC=EF,则AC的对应边是__________,∠ACB的对应角是__________.
11. 如图所示,把△ABC沿直线BC翻折180°到△DBC,那么△ABC和△DBC______全等图形(填“是”或“不是”);若△ABC的面积为2,那么△BDC的面积为__________.
E
F
C
B
A
D
12. 如图所示,△ABE≌△ACD,∠B=70°,∠AEB=75°,则∠CAE=__________°.
9题图 11题图 12题图
13. 如图所示,△AOB≌△COD,∠AOB=∠COD,∠A=∠C,则∠D的对应角是__________,图中相等的线段有__________.
13题图 14题图 15题图
14. 如图所示,已知△ABC≌△DEF,AB=4cm,BC=6cm,AC=5cm,CF=2cm,∠A=70°,∠B=65°,则∠D=__________,∠F=__________,DE=__________,BE=__________.
15.如图,点D、E分别在线段AB、AC上,BE、CD相交于点O,AE=AD,要使△ABE≌△ACD,需添加一个条件是__________(只要求写一个条件).
16. 已知:△ABC中,∠B=90°, ∠A、∠C的平分线交于点O,则∠AOC的度数为 .
17.如图,∠AOB=60°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=_________.
17题图
18题图
18.如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且DE=3 cm,BD=5 cm,则BC=_____cm.
三、解答题
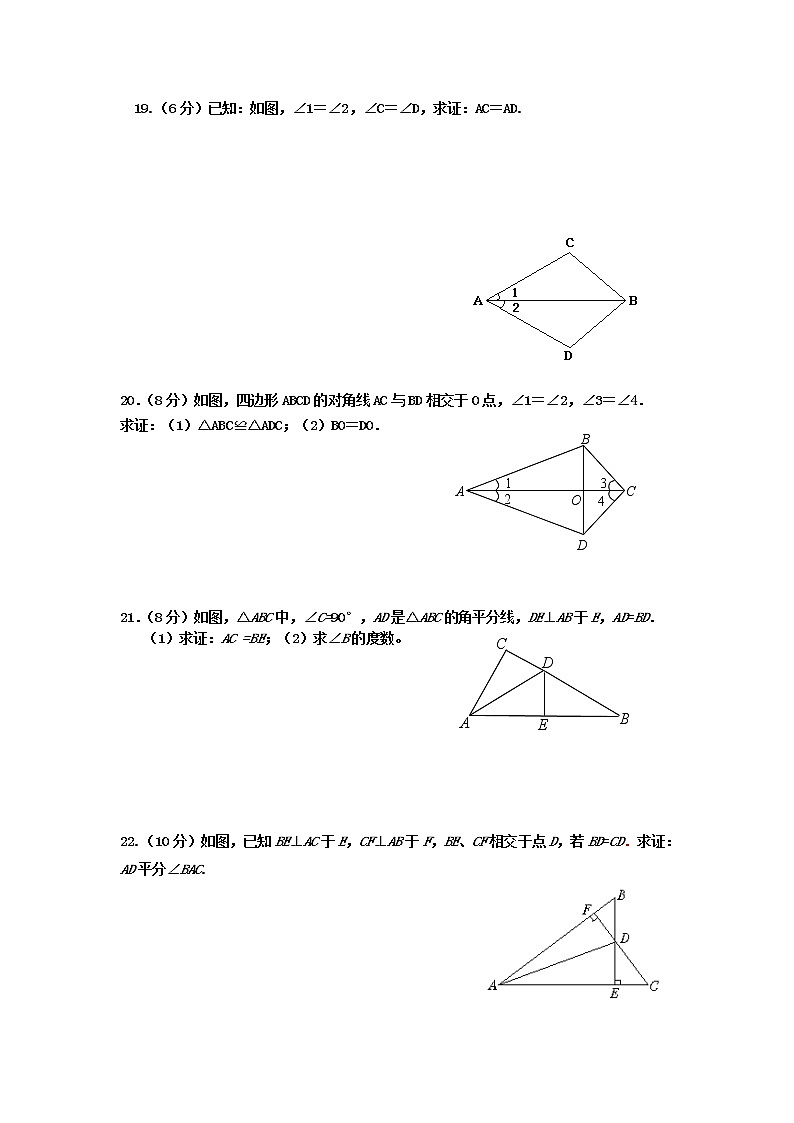
19.(6分)已知:如图,∠1=∠2,∠C=∠D,求证:AC=AD.
20.(8分)如图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.
D
C
B
A
O
1
2
3
4
求证:(1)△ABC≌△ADC;(2)BO=DO.
21.(8分)如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,AD=BD.
(1)求证:AC =BE;E
A
C
D
B
(2)求∠B的度数。
22.(10分)如图,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BD=CD.求证:AD平分∠BAC.
23.(10分)两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE.
图1
图2
D
C
E
A
B
24.(12分) MN、PQ是校园里的两条互相垂直的小路,小强和小明分别站在距交叉口C等距离的B、E两处,这时他们分别从B、E两点按同一速度沿直线行走,如图所示,经过一段时间后,同时到达A、D两点,他们的行走路线AB、DE平行吗?请说明你的理由.
轴对称测试题
(时限:100分钟 总分:100分)
班级 姓名 总分
一、 选择题(本大题共12小题,每小题2分,共24分)
1.下列几何图形中,是轴对称图形且对称轴的条数大于1的有( )
⑴ 长方形; ⑵正方形; ⑶圆; ⑷三角形; ⑸线段; ⑹射线; ⑺直线.
A. 3个 B. 4个 C. 5个 D. 6个
2.下列说法正确的是( )
A.任何一个图形都有对称轴 B.两个全等三角形一定关于某直线对称
C.若△ABC与△DEF成轴对称,则△ABC≌△DEF
D.点A,点B在直线L两旁,且AB与直线L交于点O,若AO=BO,则点A与点B关于直线L对称
3.如图所示是一只停泊在平静水面的小船,它的“倒影”应是图中的( )
4.在平面直角坐标系中,有点A(2,-1),点A关于y轴的对称点是( )
A.(-2,-1) B.(-2,1) C.(2,1) D.(1,-2)
5.已知点A的坐标为(1,4),则点A关于x轴对称的点的纵坐标为( )
A. 1 B. -1 C. 4 D. -4
6.等腰三角形是轴对称图形,它的对称轴是( )
A.过顶点的直线 B.底边上的高 C.底边的中线 D.顶角平分线所在的直线.
7.已知点A(-2,1)与点B关于直线x=1成轴对称,则点B的坐标为( )
A.(4,1) B.(4,-1) C.(-4,1) D.(-4,-1)
8.已知点P(1,a)与Q(b,2)关于x轴成轴对称,又有点Q(b,2)与
点M(m,n)关于y轴成轴对称,则m-n的值为( )
A. 3 B.-3 C. 1 D. -1
9.等腰三角形的一个内角是50°,则另外两个角的度数分别为( )
A.65°,65° B.50°,80° C.65°,65°或50°,80° D.50°,50°
10.等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角为( )
A. 30° B. 150° C. 30°或150° D.12°
11.等腰三角形底边长为6cm,一腰上的中线把它的周长分成两部分的差为2cm,则腰长为( )
A. 4cm B. 8cm C. 4cm或8cm D. 以上都不对
12.已知∠AOB=30°,点P在∠AOB的内部,点P1和点P关于OA对称,点P2和点P关于OB对称,则P1、O、P2三点构成的三角形是( )
A.直角三角形 B.钝角三角形 C.等腰直角三角形 D.等边三角形
二、填空题:(本大题共8小题,每小题3分,共24分)
13.等边三角形是轴对称图形,它有 条对称轴.
14.如图,如果△A1B1C1与△ABC关于y轴对称,那么点A的对应点A1的坐标为
15.如图是某时刻在镜子中看到准确时钟的情况,则实际时间是 .
16.已知∠AOB=30°,点P在OA上,且OP=2,点P关于直线OB的对称点是Q,则PQ= .
17.等腰三角形顶角为30°,腰长是4cm,则三角形的面积为 .
18.点P(1,2)关于直线y=1对称的点的坐标是 ;关于直线x=1对称的的坐标是 .
19.三角形三内角度数之比为1∶2∶3,最大边长是8cm,则最小边的长是 .
20.在△ABC和△ADC中,下列3个论断:①AB=AD;②∠BAC=∠DAC;③BC=DC.将两个论断作为条件,另一个论断作为结论构成一个命题,写出一个真命题 :
.
三、解答题:(本大题共52分)
21.(每小题5分,共10分)作图题:(不写作法,保留作图痕迹)
⑴ 如图,已知线段AB和直线L,作出与线段AB关于直线L对称的图形.
⑵ 已知∠AOB和C、D两点,求作一点P,使PC=PD,且P到∠AOB两边的距离相等.
22.(5分)如图所示,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
⑴求出△ABC的面积.
⑵ 在图形中作出△ABC关于y轴的对称图形△A1B1C1.
⑶ 写出点A1,B1,C1的坐标.
23.(5分)如图所示,梯形ABCD关于y轴对称,点A的坐标为(-3,3),
点B的坐标为(-2,0).
⑴ 写出点C和点D的坐标;
⑵ 求出梯形ABCD的面积.
24.(5分)如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm.
求△ABC的周长.
25.(6分)如图,D是等边三角形ABC内一点,DB=DA,BP=AB,∠DPB=∠DBC.
求证:∠BPD=30°.
26.(8分)如图,△ABC为任意三角形,以边AB、AC为边分别向外作等边三角形ABD和等边三角形ACE,连接CD、BE并且相交于点P.
求证:⑴CD=BE. ⑵∠BPC=120°
27.(6分)下面有三个结论:
⑴ 等腰三角形两底角的平分线的交点到底边两端的距离相等.
⑵ 等腰三角形两腰上中线的交点到底边两端的距离相等.
⑶ 等腰三角形两腰上的高的交点到底边两端的距离相等.
请你任选一个结论进行证明.
28.(7分)如图,在△ABC中,AB=AC,∠A=120°,BC=6,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,
求证:BM=MN=NC.
2011—2012学年度第一学期
九年级数学基础测试题
(第13章 《实数》 练习时间60分钟)
班别______________姓名_____________学号_____________成绩_____________
(一)、精心选一选(每小题4分,共24分)
1. 有下列说法:
(1)无理数就是开方开不尽的数; (2)无理数包括正无理数、零、负无理数;
(3)无理数是无限不循环小数;(4)无理数都可以用数轴上的点来表示。
其中正确的说法的个数是( )
A.1 B.2 C.3 D.4
2.如果一个实数的平方根与它的立方根相等,则这个数是( )
A. 0 B. 正整数 C. 0和1 D. 1
3.能与数轴上的点一一对应的是( )
A 整数 B 有理数 C 无理数 D 实数
4. 下列各数中,不是无理数的是 ( )
A. B. 0.5 C. 2 D. 0.151151115…
5.的平方根是( )
A. B. C. D.
6. 下列说法正确的是( )
A. 0.25是0.5 的一个平方根
B..正数有两个平方根,且这两个平方根之和等于0
C. 7 2 的平方根是7
D. 负数有一个平方根
(二)、细心填一填 (每小题4分,共24分)
7.在数轴上表示的点离原点的距离是 。设面积为5的正方形的边长为 ,那么=
8. 9的算术平方根是 ;的平方根是 ,的立方根是 , -125的立方根是 .
9. 的相反数是 ,= ;
10. ; ; = . = .
11. 比较大小: ; ; (填“>”或“<”)
12. 要使有意义,x 应满足的条件是
(三)、用心做一做 (52分,大概7小题)
13.(6分)将下列各数填入相应的集合内。
-7,0.32, ,0,,,,,0.1010010001…
①有理数集合{ … }
②无理数集合{ … }
③负实数集合{ … }
14.化简(每小题5分,共20分)
① +3—5 ② (-)
③ | | + ||- | | ④
15.求下列各式中的x(10分,每小题5分)
(1) (2)
16.比较下列各组数的大少(5分)
(1) 4 与
17. 一个底为正方形的水池的容积是486m3,池深1.5m,求这个水底的底边长.(5分)
18.一个正数a的平方根是3x―4与2―x,则a是多少?(6分)
八年级数学第十四章测试题
一、填空题(每小题3分,共27分)
1、若函数是正比例函数,则常数m的值是 。
2、平方根与立方根相等的数是 ;
3、从A地向B地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t分钟(t3),则需付电话费y(元)与t(分钟)之间的函数关系式是 。
4、某市自来水公司为了鼓励市民节约用水,采取分段收费标准,某市居民每月交水费y(元)与水量x(吨)的函数关系如图所示,请你通过观察函数图象,回答自来水公司收费标准:若用水不超过5吨,水费为 元/吨;若用水超过5吨,超过部分的水费为 元/吨。
5.等腰三角形是轴对称图形,它的对称轴是 ;
6.等腰三角形的顶角的外角度数为130o,则底角的度数为 ;
7、如图1,△ABC≌△AED,∠D=40O,∠B=45O,则∠C= ;∠DAE= ;
A
B
C
F
E
D
图3
aaE
B
A
D
C
图1
8.如图2,点A、B、C、D在同一条直线上,AB=CD,DE∥AF,要使△ACF≌△DBE,则还需要添加一个条件: (只需写一个条件)
9、学校阅览室有能坐4 人的方桌,如果多于4 人,就把方桌拼成一行,2张方桌拼成一行能坐6 人,如图所示,请你结合这个规律,填写下表:
拼成一行的桌子数
1
2
3
4
……
n
人 数
4
6
8
……
二、 选择题(每小题3分,共15分,每小题只有一个正确答案)
10.如图,BI,CI分别是∠ABC和∠ACB的平分线,
DE过I点且DE∥BC,则下列结论正确的是( )
A.AI平分∠BAC B.I到三边的距离相等
C.AI=AE D.DE=BD+CE
11.点A(-3,-4)关于y轴对称点是( )
A.(3,-4) B.(-3,4)
C.(3,4) D.(-4,3)
12、一次函数y=kx+b满足kb>0且y随x的增大而减小,则此函数的图
象不经过( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
13、已知下列等式:①-|-2|=2;②;③;④。其中正确的有( )个; A、1 B、2 C、3 D、4
14、如图8,在RT△ABC中,∠C=90O,AD平分∠BAC交BC于点D,若BC=32,且
BD﹕DC=9﹕7,则点D到AB的距离为( )
A
C
D
B
图8
A、12 B、14 C、16 D、18
15、“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟先到了终点。用S1、S2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事相吻合的是………( )
A. B. C. D.
三、解答题(第16题和第17题各6分)
16、计算:; 17、解方程:8(x-1)3=27;
18.(8分)如图将一个直角三角尺ABC绕着30°角的顶点B顺时针旋转,使点A转到CB的延长线上的点E处。(1)三角尺旋转了多少度?(2)判断△CBD的形状并说明理由;(3)求∠BDC的度数。
19.(12分)已知:一个正比例函数和一个一次函数的图像交于点P(-2、2)且一次函数的图像与y轴的交点Q的纵坐标为4。
(1)求这两个函数的解析式;(2)在同一坐标系中,分别画出这两个函数的图像;(3)求△PQO的面积。
20、(9分)画出函数的图象,利用图象:(1)求方程的解;(2)求不等式>0的解;(3)若,求的取值范围。
21、(10分)小强骑自行车去郊游,右图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象,小强9点离开家,15点回家,根据这个图象,请你回答下列问题:
(1)小强到离家最远的地方需要几小时?此时离家多远?
(2)何时开始第一次休息?休息时间多长?
(3)小强何时距家21km?(写出计算过程)
22、(10分)网络时代的到来,很多家庭都接入了网络,电信局规定了拨号入网的两种收费方式,用户可以任选其一:A:计时制:0.05元/分;B:全月制:54元/月(限一部个人住宅电话入网)。此外B种上网方式要加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,两种收费方式的费用分别为y1(元)、y2(元),写出y1、y2与x之间的函数关系式。
(2)在上网时间相同的条件下,请你帮该用户选择哪种方式上网更省钱?
23、(14分)某服装厂现有A种布料70m,B种布料52m,现计划用这两种布料生产M、N两种型号的时装80套。已知做一套M型号的时装需要A种布料0.6m,B种布料0.9m,可获利45元;做一套N型号的时装需要A种布料1.1m,B种布料0.4 m,可获利50元。若设生产N型号的时装套数为x,用这批布料生产这两种型号的时装所获的总利润为y元。
(1)求y与x的函数关系式,
(2)求出x的取值范围;
(3)该服装厂在生产这批时装中,当生产N型号的时装多少套时,所获利润最大?最大利润是多少?
四、附加题(此大题满分20分)
16、如图,直线与x轴y轴分别交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0)。
(1)求的值;
(2)若点P(,)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当点P运动到什么位置时,△OPA的面积为,并说明理由。
第15章整式测试题
一、 填空题(每空2分,共26分):
1. ______ , _____ _ .
2. 合并同类项:____ __ .
3. , 则______ .
4. , . 则______ .
5. ____ __ .
6. 如果是一个完全平方式, 则的值为____ __ .
7. ______ , ______ .
8. ___ ___.
9. __ ____ .
10. =___ ___ .
11. 边长分别为和的两个正方形按如图(I)的样式摆放,
则图中阴影部分的面积为 .
二、选择题(每题2分,共18分):
12.下列计算结果正确的是( )
A B
C D
13.下列运算结果错误的是( )
A
B
C
D
14. 给出下列各式①,②,③,
④,⑤,⑥.
其中运算正确有( )
A 3个 B 4个 C 5 个 D 6个
15.下列各式中,计算结果是的是( )
A B
C D
16.下列各式计算中,结果正确的是( )
A
B
C
D
17.在下列各式中,运算结果为的是( )
A B
C D
18.下列计算中,正确的是( )
A
B
C
D
19. 的运算结果正确的是( )
A B C D
20. 若,则有( )
E B
C D
二、 计算题(每小题5分,共35分):
21. .
22. .
23. .
24. .
25. .
26. .
27. 应用乘法公式进行计算:.
四、解答题(每小题5分,共10分);
28. 先化简,再求值:,其中.
1.
29. 解方程:
五、(30小题5分,31小题6分,共11分)
30. 已知:为不等于0的数,且,求代数式的值.
31.已知:,,求-的值.
2011-2012人教版八年级数学上册期末试卷一
一、 选择题(每小题3分,共18分)
下列各小题均有四个答案,其中只有一个是正确的,将正确答案的代号字母填入题后括号内。
1. 的相反数是( )
A. B. C. D.
2. 的角平分线AD交BC于 点D,,则点D到AB的距离是( )
A.1 B.2 C.3 D.4
3. 下列运算正确的是( )
A. B.
C. D.
4. 到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
5. 一次函数的图象大致是( )
A.
B.
C.
D.
6. 如图,已知中,,,是高和的交点,则线段D
C
B
A
E
H
的长度为( )
A. B.4 C. D.5
二、填空题(每小题3分,共27分)
7. 计算: .
1
2
0
A
B
C
8. 如图,数轴上两点表示的数分别是1和,点关于点 的对称点是点,则点所表示的数是 .
9. 随着海拔高度的升高,空气中的含氧量与大气压强成正比例函数关系.当时,,请写出与的函数关系式 .
10. 因式分解: .
11. 如图,一次函数的图象经过A、B两点,则关于x的不等式的解集是 .
第11题图 第13题图
12. 已知,则______________.
13. 如图,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为(a+2b)、宽为(a+b)的大长方形,则需要C类卡片 张.
14. 直线经过点和轴正半轴上的一点,如果(为坐标原点)的面积为2,则的值为 .
15. 在平面直角坐标系中,已知点,点是轴上的一个动点,当是等腰三角形时,值的个数是 .
三、解答题(本大题8个小题,共75分)
16.(8分)计算:.
17. (8分) 如图,有两个的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
(1)线段的一个端点为梯形的顶点,另一个端点在梯形一边的格点上;
(2)将梯形分成两个图形,其中一个是轴对称图形;
(3)图1、图2中分成的轴对称图形不全等.
图1
图2
18. (9分)(1) 分解因式:.
(2) 先化简,再求值:,其中.
l9.(9分) 把两个含有45°角的直角三角板如图放置,点D在BC上,连结BE,AD,AD的延长线交BE于点F.
求证:AF⊥BE.
A
F
B
C
E
D
20.(9分) 在市区内,我市乘坐出租车的价格(元)与路程(km)的函数关系图象如图所示.
6
5
2
2.625
(1)请你根据图象写出两条信息;
(2)小明从学校出发乘坐出租车回家用了13元,求学校离小明家的路程.
21. (10分) 如图,在等边中,点分别在边上,且,与交于点.
D
A
E
F
B
C
(1)求证:;
2)求的度数.
22. (10分) 康乐公司在两地分别有同型号的机器台和台,现要运往甲地台,乙地台,从两地运往甲、乙两地的费用如下表:
甲地(元/台)
乙地(元/台)
地
地
(1)如果从地运往甲地台,求完成以上调运所需总费用(元)与(台)之间的函数关系式;
(2)请你为康乐公司设计一种最佳调运方案,使总费用最少,并说明理由。
23.(12分)已知:点到的两边所在直线的距离相等,且.
(1)如图1,若点在边上,求证:;
图1
图2
A
A
B
B
C
C
E
F
O
O
(2)如图2,若点在的内部,求证:;
(3)若点在的外部,成立吗?请画图表示.
2011-2012八年级第一学期期末练习
数学试卷二 2012.01
1. 的绝对值是( )
A. B. C. D.
2. 若分式的值为0,则( )
A. B. C. D.
3. 如图,是等边三角形,点D在AC边上,,则的度数为( )
A. B. C. D.
4. 下列计算正确的是( )
A. B. C. D.
5. 小彤的奶奶步行去社区卫生院做理疗,从家走了15分钟到达距离家900米的社区卫生院,她用了20分钟做理疗,然后用10分钟原路返回家中,那么小彤的奶奶离家的距离S(单位:米)与时间t(单位:分)之间的函数关系图象大致是( )
6. 已知一个等腰三角形两边长分别为5,6,则它的周长为( )
A. B.
C.或 D.或
7. 根据分式的基本性质,分式可变形为( )
A. B. C. D.
8. 已知,则的值为( )
A. B. C. D.
9. 如图,BD是的角平分线,,DE交AB于E,若,则下列结论中错误的是( )
A. B.
C. D.
10. 已知定点M(,)、N(,)()在直线上,若,则下列说明正确的是( )
①是比例函数;②是一次函数;
③是一次函数;④函数中随的增大而减小;
A.①②③ B.①②④ C.①③④ D.①②③④
11. 9的平方根是_____.
12. 分解因式:_________________.
13. 函数的自变量x的取值范围是_______.
14. 如图在中,,,
AB的垂直平分线MN交AC于D,
则_______度.
15. 如图,直线与坐标轴交于A(,0),B(0,5)两点,
则不等式的解集为_________.
16. 观察下列式子:
第1个式子:;第2个式子:
第3个式子:;……
按照上述式子的规律,第5个式子为;
第n个式子为_______________________________(n为正整数)
17. 计算:(1); (2).
18. 如图,在正方形网格中,阴影部分是由5个小正方形组成的一个图形,请你用两种方法分别在下图方格内添涂2个小正方形,使这7个小正方形组成的图形是轴对称图形。
19. 先化简,再求值:,其中.
20. 如图,中,,AM是BC边上的中线,点N在AM上,求证.
21. 如图,已知直线经过点A(4,3),与y轴交于点B。
(1)求B点坐标;
(2)若点C是x轴上一动点,当的值最小时,求C点坐标.
22. 如图,在四边形ABCD中,,,DE交BC于E,交AC于F,,。
(1)求证:是等腰三角形;
(2)若,求CD的长。
23. 小丽想用一块面积为的正方形纸片,沿着边的方向裁出一块面积为的长方形纸片,使它长宽之比为,请你说明小丽能否用这块纸片裁出符合要求的长方形纸片。
24. 如图,AD是的角平分线,H,G分别在AC,AB上,且.
(1)求证:与互补;
(2)若,请探究线段AG与线段AH、HD之间满足的等量关系,并加以证明。
25. 设关于一次函数与,我们称函数(其中)为这两个函数的生成函数。
(1)请你任意写出一个与的生成函数的解析式;
(2)当时,求与的生成函数的函数值;
(3)若函数与的图象的交点为P(a,5),当时,求代数式的值.
26. 已知A(,),B(,),点C与点A关于坐标原点对称,经过点C的直线与y轴交于点D,与直线AB交于点E,且E点在第二象限。
(1)求直线AB的解析式;
(2)若点D(0,1),过点B作于F,连接BC,求的度数及的面积;
(3)若点G(G不与C重合)是动直线CD上一点,且,试探究与之间满足的等量关系,并加以证明。
2012—2013八年级上学期数学期末复习题及答案三
一、选择题(每小题3分,共30分):
1.下列运算正确的是( )
A.= -2 B.=3 C. D.=3
2.计算(ab2)3的结果是( )
A.ab5 B.ab6 C.a3b5 D.a3b6
3.若式子在实数范围内有意义,则x的取值范围是( )
A.x>5 B.x5 C.x5 D.x0
4.如图所示,在下列条件中,不能判断△ABD≌
△BAC的条件是( )
A.∠D=∠C,∠BAD=∠ABC
B.∠BAD=∠ABC,∠ABD=∠BAC
C.BD=AC,∠BAD=∠ABC
D.AD=BC,BD=AC
5.下列“表情”中属于轴对称图形的是( )
A. B. C. D.
6.在下列个数:301415926、、0.2、、、、中无理数的个数是( )
A.2 B.3 C.4 D.5
7.下列图形中,以方程y-2x-2=0的解为坐标的点组成的图像是( )
8.任意给定一个非零实数,按下列程序计算,最后输出的结果是( )
A.m B.m+1 C.m-1 D.m2
9.如图,是某工程队在“村村通”工程中修筑的公路长度(m)与时间(天)之间的关系图象,根据图象提供的信息,可知道公路的长度为( )米.
A.504 B.432 C.324 D.720
10.如图,在平面直角坐标系中,平行四边形ABCD的顶点A、B、D的坐标分别为(0,0)、(5,0)、(2,3),则顶点C的坐标为( )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
二、填空题(每小题3分,共18分):
11.若+y2=0,那么x+y= .
12.若某数的平方根为a+3和2a-15,则a= .
13.等腰三角形的一个外角是80°,则其底角是 .
14.如图,已知:在同一平面内将△ABC绕B点旋转到△A/BC/的位置时,AA/∥BC,∠ABC=70°,∠CBC/为 .
15.如图,已知函数y=2x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式2x+b>ax-3的解集是 .
16.如图,在△ABC中,∠C=25°,AD⊥BC,垂足为D,且AB+BD=CD,则∠BAC的度数是 .
三、解答题(本大题8个小题,共72分):
17.(10分)计算与化简:
(1)化简:0;
(2)计算:(x-8y)(x-y).
18.(10分)分解因式:
(1)-a2+6ab-9b2;
(2)(p-4)(p+1)+3p.
19.(7分)先化简,再求值:(a2b-2ab2-b3)÷b-(a+b)(a-b),其中a=1/2,b= -1.
20.(7分)如果为a-3b的算术平方根,为1-a2的立方根,求2a-3b的平方根.
21.(8分)如图,在△ABC中,∠C=90°,AB的垂直平分线交AC于点D,垂足为E,若∠A=30°,CD=2.
(1)求∠BDC的度数; (2)求BD的长.
22.(8分)如图,在平面直角坐标系中,点P(x,y)是第一象限直线y=-x+6上的点,点A(5,0),O是坐标原点,△PAO的面积为S.
(1)求s与x的函数关系式,并写出x的取值范围;
(2)探究:当P点运动到什么位置时△PAO的面积为10.
23.(10分)2008年6月1日起,我国实施“限塑令”,开始有偿使用环保购物袋. 为了满足市场需求,某厂家生产A、B两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产A种购物袋x个,每天共获利y元.
(1)求出y与x的函数关系式;
(2)如果该厂每天最多投入成本10000元,那
么每天最多获利多少元?
第十二章参考答案和提示:
一、 选择题:1.C;2.C;3.B;4.A;5.D;6.D;7.A;8.B;9.C;10.C;11.C;12.D;
二、填空题:13. 3;14.(-1,3);15. 4点40分;16. 2;17. 4cm2;18.(1,0),(1,2);
19.4cm;20.等腰三角形的顶角平分线和底边上的中线重合.
三、解答题:21.略;
22.⑴=×5×3=7.5(平方单位);⑵略;⑶A1(1,5),B1(1,0);C1(4,3).
23.⑴C(2,0),D(3,3).⑵=(4+6)×3=15(平方单位).
24.∵DE是线段AC的垂直平分线
∴AD=CD
∵△ABD的周长为13cm
∴AB+BC=13cm
∵AE=3cm
∴AC=2AE=6cm. ∴△ABC的周长为:AB+BC+AC=19cm.
25.连接CD,并延度CD交AB于E,证CE垂直平分AB,可得∠DCB=30°
再证△BDC≌△BDP即可.
26.略;
27.略
28.连接MA、NA,证明:MA=NA=MN.
第十三章参考答案
(一)、精心选一选(每小题4分,共24分)
1.B 2.A 3.D 4.B 5.B 6.B
(二)、细心填一填(每小题4分,共24分)
7.、
8. 3 、 、 、 -5
9. 、
10. 4 、 -6 、196 、 -2
11. > ; > ;
12.
(三)、用心做一做
13.(6分)将下列各数填入相应的集合内。
-7,0.32, ,0,,,,,0.1010010001…
①有理数集合{ -7, 0.32, , 0, ,… } 2分
②无理数集合{ , , , 0.1010010001… … } 2分
③负实数集合{ -7, , … } 2分
14.化简(每小题5分,共20分)
① +3—5
解:原式=(1+3-5) 3分
= 2分
② (-)
解:原式= -() 2分
=1-7 2分
=-6 1分
③ | | + ||- | |
解:原式= + - 3分
= 2分
④
解:原式= 2+2- 3分
= 2分
15.求下列各式中的x(10分,每小题5分)
(1) (2)
解: 解:
2分 2分
2分 2分
1分 1分
16.比较下列各组数的大少(5分)
(1) 4 与
解:∵ ,=63 2分
又∵能 1分
∴ 2分
17. 一个底为正方形的水池的容积是486m3,池深1.5m,求这个水池的底边长.(5分)
解:设这个水池的底边长为x,则 1分
1分
2分
答:这个水池的底边长为18米。 1分
18.一个正数a的平方根是3x―4与2―x,则a是多少?(6分)
解:由题意得: 2分
2分
∴ 1分
∴ =1 1分
第十四章测试题答案
1..
2..
3..
4.0.72;0.9.
5.10;.
6.B.
7.A.
8.A.
9.D.
10.B.
11..
12.(1);(2);(3).
13.(1)3小时,30千米;(2)10点半;半小时;(3)小强在11:24时和13:36时距家21.
14.(1);(2)当用户某月上网时间超过30小时时,选择B种上网方式更省钱; 当上网时间为30小时时,两种上网方式费用一样; 当上网时间少于30小时时,选择A种上网方式更省钱 .
15.(1);(2)当生产N型号的时装44套时,所获利润最大,最大利润是3820元.
16.(1);(2)(3)当P点的坐标为时,△OPA的面积为.
数学期末试题一参考答案及评分标准
一、 选择题(每小题3分,共18分B B B D B B
二、 填空题(每小题3分,共27分)
7., 8., 9., 10., 11.x<2, 12., 13.3, 14. 2,
15.4个.
三、解答题
16.解:原式= (6分)
(8分)
17.解:提供以下方案供参考.
(画对1种,得4分;画对2种,得8分)
18.(1)解: . (4分)
(2)解:原式=
=. (4分)
当时,原式=. (5分)
19.解:(1)证明:在△ACD和△BCE中,
A
F
B
C
E
D
AC=BC,
∠DCA=∠ECB=90°,
DC=EC,
∴ △ACD≌△BCE(SAS). 5分
∴ ∠DAC=∠EBC. 6分
∵ ∠ADC=∠BDF,
∴ ∠EBC+∠BDF=∠DAC+∠ADC=90°.
∴ ∠BFD=90°. 8分
∴ AF⊥BE. 9分
20.解:(1)在0到2km内都是5元;2km后,每增加0.625km加1元. 2分
(答案不唯一)
(2)设函数表达式为.依题意,得 3分
解得:.得. 7分
将代入上式,得. 8分
所以小明家离学校7km. 9分
21.(1)证明:是等边三角形,
,
又
, 4分
. 5分
(2)解由(1),
得 6分
10分
22.解:(1); 5分
(2)由(1)知:总运费.
,又, 8分
随的增大,也增大,当时,(元).9分
该公司完成以上调运方案至少需要14800元运费,最佳方案是:由地调3台至甲地,14台至乙地,由地调15台至甲地. 10分
23. 证:(1)过点分别作,,分别是垂足,
A
B
E
F
O
C
由题意知,,,
,
,从而. 3分
(2)过点分别作,,分别是垂足,
由题意知,.
在和中,
,,.
,
又由知,?,. 9分
解:(3)不一定成立. 10分
(注:当的平分线所在直线与边的垂直平分线重合时,有;否则,.如示例图)
A
B
C
E
F
O(成立)
O(不成立)
A
B
C
E
F
12分
八年级第一学期期末练习
数学参考答案与评分标准 2012.1
一、选择题(本题共30分,每小题3分)
1. A 2.B 3. D 4.C 5.D 6.C 7. A 8.B 9.C 10.B
二、填空题(本题共18分,每小题3分)
11. ±3 12. y (x-1)2 13. x¹ -5 14. 30 15.
16. 61, 60 ( 1分) ; (2n2+2n+1) 2-(2n2+2n) 2 =(2n+1)2 ( 2分)
三、解答题(本题共52分;第17题8分;第18 题~第21题各4分;第22题~第24题
各5分; 第25题6分; 第26题7分)
说明:解法不同于参考答案, 正确者可参照评分标准相应给分.
………………………………………………3分
………………………………………………4分
(2) (2a-b) 2+ (a+b)(4a-b)
=4a2 -4ab+b2 +4a2 -ab+4ab-b2 ………………………………………………3分
=8a2-ab. ……………………………………………………………………4分
18. 答案不唯一,参见下图. 正确画出一个图给2分; 累计4分.
………………………………………………2分
………………………………………………3分
N
M
A
B
C
………………………………………………4分
当时, 原式=
20. 证明: ∵ AB=AC, AM是BC边上的中线,
∴ AM^BC. ………………………………………………2分
∴ AM垂直平分BC.
∵ 点N在AM上,
∴ NB=NC. ………………………………………………4分
21. 解:(1)由点A (4, 3)在直线上, 得
b=1.
∴ B(0, 1). ………………………………………1分
(2) 如图, 作点A (4, 3)关于x轴的对称点A¢ (4, -3),
连接BA¢交x轴于点C, 则此时AC+BC取得最小值. …………………………………2分
设直线BA¢的解析式为, 依题意
-3=4k+1.
k=-1.
∴ 直线BA¢的解析式为. …………………………………………………3分
令y=0, 则x=1.
∴ C(1, 0). …………………………………………………4分
22.解: (1) 证明:∵ DE//AB, ∠B=90°,
∴ ∠DEC=90°.
∴ ∠DCE=90°-∠CDE=60°.
∴ ∠DCF=∠DCE -∠ACB=30°.
∴ ∠CDE=∠DCF. …………………………………………………1分
∴ DF=CF.
∴ △FCD是等腰三角形. …………………………………………………2分
F
E
D
C
B
A
(2) 解: 在△ACB和△CDE中,
∴ △ACB≌△CDE.
∴ AC=CD. …………………4分
在Rt△ABC 中, ∠B=90°, ∠ACB=30°,AB=4,
∴ AC=2AB=8.
∴ CD =8. …………………………………………………………5分
23. 解:设长方形纸片的长为3x (x>0)cm,则宽为2x cm,依题意得
3x×2x=300. ……………………………………………………………………2分
6x2=300.
x2=50.
∵ x>0,
∴ x =. ……………………………………………………………………3分
∴ 长方形纸片的长为3cm.
∵ 50>49,
∴>7.
∴ 3>21, 即长方形纸片的长大于20cm. …………………………………………4分
由正方形纸片的面积为400 cm2, 可知其边长为20cm,
∴ 长方形的纸片长大于正方形纸片的边长.
答: 小丽不能用这块纸片裁出符合要求的长方形纸片. …………………………5分
24. 解:(1)证明:在AB上取一点M, 使得AM=AH, 连接DM.
∵ ∠CAD=∠BAD, AD=AD,
∴ △AHD≌△AMD. ……………………1分
∴ HD=MD, ∠AHD=∠AMD.
∵ HD=DB,
∴ DB= MD.
∴ ∠DMB=∠B. …………………………2分
∵ ∠AMD+∠DMB =180°,
∴ ∠AHD+∠B=180°. ………………………3分
即 ∠B与∠AHD互补.
(2)由(1)∠AHD=∠AMD, HD=MD, ∠AHD+∠B=180°.
∵ ∠B+2∠DGA =180°,
∴ ∠AHD=2∠DGA.
∴ ∠AMD=2∠DGM.
∵ ∠AMD=∠DGM+∠GDM.
∴ 2∠DGM=∠DGM+∠GDM.
∴ ∠DGM=∠GDM. ………………………………………………………………4分
∴ MD=MG.
∴ HD= MG.
∵ AG= AM+MG,
∴ AG= AH+HD. ……………………………………………………………5分
25. 解:(1)答案不唯一. 比如取m =2时, n=-1.
生成函数为y=2(x+1)-(3x-1)=-x+3,即y=-x+3. ……………………………1分
(2)当x=c时,y=m(x+c)+n(3x-c)=2c(m+n). ……………………………………………2分
∵,
∴ y=2c(m+n)=2c . ……………………………………………3分
(3)法一:∵点 P (a, 5) 在与的图象上,
∴ ,. …………………………………………………4分
∴ a12a2+b12=( a1a+b1)2 -2 aa1b1 =52 -2 aa1b1, a22a2+b22= (a2a+b2)2 -2aa2b2=52 -2aa2b2.
…………………………………………………5分
当 a1b1= a2b2=1时,
m(a12a2+b12) +n (a22a2+b22)+ 2ma+2na = m (52 -2a ) + n(52 -2a) + 2ma+2na =25(m+n).
∵,
∴ m(a12a2+b12) +n(a22a2+b22)+ 2ma+2na =25(m+n)=25. ……………………………6分
法二:∵点P(a, 5)在与的图象上,
∴ ,. …………………………………………………4分
当 a1b1= a2b2 =1时,
m (a12a2+b12) +n (a22a2+b22)+2ma+2na= m (a12a2 +2aa1b1+b12) +n (a22a2 +2aa2b2+b22)
=m(a1a+b1) 2+ n (a2a+b2) 2 …………………………………………………5分
=m×52+n×52=25(m+n).
∵ m+n=1,
∴ m (a12x2+b12) +n (a22x2+b22)+2ma+2na=25(m+n)=25. ……………………………6分
26. 解:(1)依题意,设直线AB的解析式为.
∵ A(-1,0)在直线上,
∴ 0= -k-3. ∴ k=-3.
∴直线AB的解析式为. …………………………………………1分
(2)如图1,依题意,C(1,0),OC=1.
由D(0,1),得OD=1.
在△DOC中,∠DOC=90°,OD=OC=1.
可得 ∠CDO=45°.
∵ BF⊥CD于F,
∴ ∠BFD=90°.
∴ ∠DBF=90°-∠CDO =45°. …………………2分
可求得直线CD的解析式为 图1
由 解得
∴ 直线AB与CD的交点为E(-2,3). …………………………………………3分
过E作EH⊥y轴于H, 则EH=2.
∵ B(0,- 3), D(0,1),
∴ BD=4.
∴ ………………………………4分
图2
(3)连接BC, 作BM⊥CD于M.
∵ AO=OC,BO⊥AC,
∴ BA=BC.
∴ ∠ABO=∠CBO.
设 ∠CBO=a,则∠ABO=a,∠ACB=90°-a.
∵ BG=BA,
∴ BG=BC.
∵ BM⊥CD,
∴ ∠CBM=∠GBM.
图3
设∠CBM=b,则∠GBM=b,∠BCG=90°-b.
(i) 如图2,当点G在射线CD的反向延长线上时,
∵ ∠ABG=
∠ECA=
∴ ∠ABG=2∠ECA. ……………………6分
(ii) 如图3,当点G在射线CD的延长线上时,
∵ ∠ABG=
∠ECA=
∴ ∠ABG=2∠ECA. ……………………7分
综上,∠ABG=2∠ECA.
说明:第(3)问两种情况只要做对一种给 2分;累计3分.
期末三参考答案:
一、选择题:
BDBCC.ACBAC.
二、填空题:
11.2; 12.4; 13.40o; 14.40o; 15.x>-2; 16.105o.
三、解答题:
17.(1)解原式=3=;
(2)解:(x-8y)(x-y)=x2-xy-8xy+8y2=x2-9xy+8y2.
18.(1)原式=-(a2-6ab+9b2)=-(a-3b)2;
(2)原式=p2-3p-4+3p=p2-4=(p+2)(p-2).
19.解原式=a2-2ab-b2-(a2-b2)=a2-2ab-b2-a2+b2=-2ab,
将a=,b=-1代入上式得:原式=-2××(-1)=1.
20.解:由题意得:,解得:,
∴2a-3b=8,∴±.
21.(1)∵DE垂直平分AB,∴DA=DB,∴∠DBE=∠A=30°,∴∠BDC=60°;
(2)在Rt△BDC中,∵∠BDC=60°,∴∠DBC=30°,∴BD=2CD=4.
22.解:(1)s=-x+15(0
23.解:(1)根据题意得:y=(2.3-2)x+(3.5-3)(4500-x)=-0.2x+2250;
(2)根据题意得:2x+3(4500-x)≦10000,解得:x≧3500元.
∵k=-0.2<0,∴y随x的增大而减小,
∴当x=3500时,y=-0.2×3500+2250=1550.
答:该厂每天至多获利1550元.
人教版八年级上册数学期末测试题: 这是一份人教版八年级上册数学期末测试题,共8页。试卷主要包含了分解因式等内容,欢迎下载使用。
最新人教版八年级上册数学期末试卷及答案: 这是一份最新人教版八年级上册数学期末试卷及答案,共6页。
最新人教版八年级上册数学期末考试试卷及答案: 这是一份最新人教版八年级上册数学期末考试试卷及答案,共5页。













