浙江省杭州地区(含周边)重点中学2021-2022学年高三上学期期中考试数学试题
展开浙江省杭州地区(含周边)重点中学2021-2022学年高三上学期期中考试数学试题
选择题部分
一、选择题: 本大题共 10 小题, 每小题 4 分, 共 40 分。在每小题给出的四个选项中, 只有一项是 符合题目要求的。
1. 设集合 , 则 ( )
A. B.
C. D.
2. 设 ( 为虚数单位), 则 ( )
A. B. C. 3 D. 2
3. 若实数 满足约束条件 ( )
A. B. C. D.
展开式中, 的系数为( )
A. 20 B. C. 160 D.
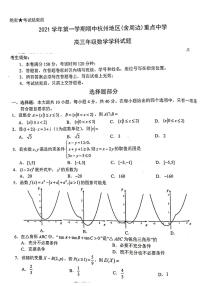
5. 函数 的图象可能是( )
6. 在 角形 中, "tan "是“ 为锐角三角形”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
7. 设随机变量 , 若 , 则 ( )
A. B. C. D. 1
8. 对于平面内不共线的四点 , 若存在一组正实数 , 使得 , 则三个角 ( )
A. 都是钝角 B. 至少有两个钝角
C. 恰有两个钝角 D. 至多有两个钝角
9. 若对任意的 , 当 时, 恒有 成立, 则实数 的取值范围是( )
A. B. C. D.
10. 已知数列 , 数列 满足 恒成立, 则 可能为( )
A. B. C. D.
非选择题部分
二、填空题: 本大题共 7 小题, 多空题每题 6 分, 单空题每题 4 分, 共 36 分。
11. 《九章算术》是我国古代内容极为丰富的数学名著, 其中有这样一个问题: “今有宛田, 下周三 十步, 径十六步。问为田几何? " 其意思为: “有一块扇形的田, 弧长为 30 步, 其所在圆的直 径为 16 步, 问这块田的面积是多少平方步? " 该问题的答案为平方步。
12. 若 , 则 .
13. 在平面直角坐标系中, , 在 轴正半轴有点 , 则 的最大值为, 此时 .
14. 已知正整数 满足 , 则 的最大值为,最小值为.
15. 已知 为单位向量, 且 , 设向量 与向量 的夹角为 , 则 .
16. 男生甲和女生乙及另外 2 男 2 女共 6 位同学排成一排拍照, 要求男女生相间且甲和乙相邻, 共种不同排法。
17. 函数 的零点个数为, 则 .
三、解答题: 本大题共 5 小题, 共74分。解答应写出文字说明,证明过程或演算步骤。
18.(本题满分14分) 设函数=-,( R)
(I) 求 的最大值和对称中心;
(II) 为 的导函数, 若 , 求 的值。
19. (本题满分 15 分)如图, 在三棱雉 中,
(I)求证: ;
(II) 若直线 与平面 成 角, 求 .
20. (本题满分 15 分) 已知数列 , 且满足 。数列 满足 , 数列 的前 项和为 .
(I)证明: 数列 为等比数列并求 的通项公式;
(II) 求数列 的通项公式.
21. (本题满分 15 分) 已知点 , 直线 的斜率之积为 , 设点 的轨 迹为曲线 。
(I)求曲线 的轨迹方程;
(II) 若抛物线 与曲线 交于点 , 设 , 求 面积最大时 的值.
22. (本题满分 15 分)已知 , 直线 为曲线 在 处的切线, 直线 与曲线 相交于点 且 .
(I) 求 的取值范围;
(II) (1)证明: ;
(2)证明: .
浙江省杭州地区(含周边)重点中学2021-2022学年高二上学期期中考试数学试题含答案: 这是一份浙江省杭州地区(含周边)重点中学2021-2022学年高二上学期期中考试数学试题含答案,共8页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
2022届浙江省杭州地区(含周边)重点中学高三上学期期中考试数学试题(PDF版含答案): 这是一份2022届浙江省杭州地区(含周边)重点中学高三上学期期中考试数学试题(PDF版含答案),共8页。
浙江省杭州地区(含周边)重点中学2022届高三上学期期中考试数学试题 扫描版含答案: 这是一份浙江省杭州地区(含周边)重点中学2022届高三上学期期中考试数学试题 扫描版含答案,共8页。