2021-2022学年江苏省南京市秦淮区五校联考七年级（上）期中数学试卷

这是一份2021-2022学年江苏省南京市秦淮区五校联考七年级（上）期中数学试卷，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）5G是第五代移动通信技术，5G网络理论下载速度可以达到每秒130000KB以上，用科学记数法表示130000是（ ）
A．13×105B．1.3×105C．1.3×106D．1.3×107
2．（3分）无论x取何值，下列式子的值一定是正数的是（ ）
A．|x|B．|x2|C．|x+1|D．x2+1
3．（3分）下列各组中，不是同类项的是（ ）
A．52与25B．﹣ab与ba
C．0.2a2b与﹣a2bD．a2b3与﹣a3b2
4．（3分）如图，数轴上的点M，P，N，Q分别表示四个有理数，若点M，N表示的有理数互为相反数，则图中表示正数的点的个数是（ ）
A．1B．2C．3D．4
5．（3分）设想有一根铁丝套在地球的赤道上，刚好拉紧后，又放长了10米，并使得铁丝均匀地离开地面．则下面说法中比较合理的是（ ）
A．你只能塞过一张纸B．只能伸进你的拳头
C．能钻过一只小羊D．能驶过一艘万吨巨轮
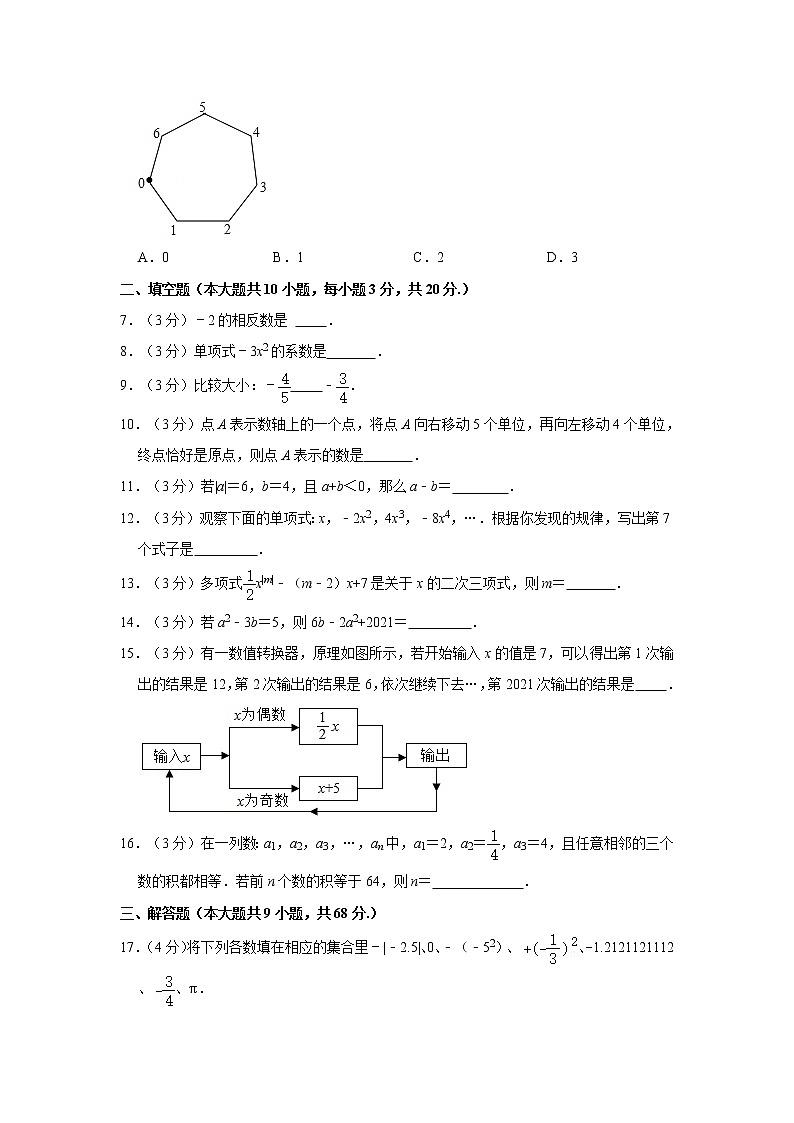
6．（3分）如图，一枚棋子放在七角棋盘的第0号角，现依逆时针方向移动这枚棋子，其各步依次移动1，2，3，…，n个角，如第一步从0号角移动到第1号角，第二步从第1号角移动到第3号角，第三步从第3号角移动到第6号角，…．若这枚棋子不停地移动下去，则这枚棋子永远不能到达的角的个数是（ ）
A．0B．1C．2D．3
二、填空题（本大题共10小题，每小题3分，共20分.）
7．（3分）﹣2的相反数是 ．
8．（3分）单项式﹣3x2的系数是 ．
9．（3分）比较大小：﹣ ﹣．
10．（3分）点A表示数轴上的一个点，将点A向右移动5个单位，再向左移动4个单位，终点恰好是原点，则点A表示的数是 ．
11．（3分）若|a|＝6，b＝4，且a+b＜0，那么a﹣b＝ ．
12．（3分）观察下面的单项式：x，﹣2x2，4x3，﹣8x4，…．根据你发现的规律，写出第7个式子是 ．
13．（3分）多项式x|m|﹣（m﹣2）x+7是关于x的二次三项式，则m＝ ．
14．（3分）若a2﹣3b＝5，则6b﹣2a2+2021＝ ．
15．（3分）有一数值转换器，原理如图所示，若开始输入x的值是7，可以得出第1次输出的结果是12，第2次输出的结果是6，依次继续下去…，第2021次输出的结果是 ．
16．（3分）在一列数：a1，a2，a3，…，an中，a1＝2，a2＝，a3＝4，且任意相邻的三个数的积都相等．若前n个数的积等于64，则n＝ ．
三、解答题（本大题共9小题，共68分.）
17．（4分）将下列各数填在相应的集合里﹣|﹣2.5|、0、﹣（﹣52）、、−1.2121121112、、π．
正数集合：{ …}；
整数集合：{ …}；
负分数集合：{ …}；
无理数集合：{ …}．
18．（12分）计算：
（1）．
（2）．
（3）．
19．（5分）先化简，再求值：x﹣2（）+（﹣），其中x＝，y＝﹣2．
20．（8分）已知四个数，a＝﹣22，b＝﹣|﹣2|，c＝﹣（﹣1）100，d＝﹣（﹣3）．
（1）计算a、b、c、d，得a＝ ，b＝ ，c＝ ，d＝ ；
（2）把这四个数在如图所示的数轴上分别表示出来．
（3）用“＜”把a、b、c、d连接起来．
（4）用“＞”把|a|、|b|、|c|、|d|连接起来．
21．（8分）定义一种新运算：观察下列式：
1⊙3＝1×4+3＝7
3⊙（﹣1）＝3×4﹣1＝11
5⊙4＝5×4+4＝24
4⊙（﹣3）＝4×4﹣3＝13
（1）请你想一想：a⊙b＝ ；
（2）若a≠b，那么a⊙b b⊙a（填入“＝”或“≠”）
（3）若a⊙（﹣2b）＝4，请计算（a﹣b）⊙（2a+b）的值．
22．（8分）已知M＝4x2﹣2x﹣1，N＝3x2﹣2x﹣5．
（1）当x＝﹣1时，求代数式4M﹣（2M+3N）的值；
（2）试判断M、N的大小关系，并说明理由．
23．（8分）运动会前夕，为了提高体能，小明每天放学回家做仰卧起坐．他制作了一张表格记录自己每天做仰卧起坐的成绩．以每分钟做40个为标准，超过的个数记为正，不足的个数记为负．下表是小明一周做仰卧起坐的记录：
根据上述记录表，回答下列问题：
（1）小明这周一天最多做 个，最少做 个；
（2）这周小明平均每天做多少个？
24．（7分）生活与数学：
（1）吉姆同学在某月的日历上圈出2×2个数，正方形的方框内的四个数的和是32，那么第一个数是 ；
（2）玛丽也在日历上圈出2×2个数，斜框内的四个数的和是42，则它们分别是 ；
（3）莉莉也在日历上圈出5个数，呈十字框形，它们的和是50，则中间的数是 ；
（4）某月有5个星期日的和是75，则这个月中最后一个星期日是 号；
（5）若干个偶数按每行8个数排成图4：
①图中方框内的9个数的和与中间的数有什么关系： ；
②汤姆所画的斜框内9个数的和为360，则斜框的中间一个数是 ；
③托马斯也画了一个斜框，斜框内9个数的和为252，则斜框的中间一个数是 ．
25．（8分）阅读下面材料：
点A、B在数轴上分别表示数a、b．A、B两点之间的距离表示为|AB|．则数轴上A、B两点之间的距离|AB|＝|a﹣b|．
回答下列问题：
（1）数轴上表示1和﹣3的两点之间的距离是 ；数轴上表示﹣2和﹣5的两点之间的距离是 ；
（2）数轴上表示x和﹣1的两点A和B之间的距离是 ，如果|AB|＝2，那么x为 ；
（3）当|x+1|+|x﹣2|取最小值时，符合条件的整数x有 ；
（4）令y＝|x+1|+|x﹣2|+|x﹣3|，问当x取何值时，y最小，最小值为多少？请求解．
2021-2022学年江苏省南京市秦淮区五校联考七年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本大题共6小题，每小题3分，共12分.）
1．（3分）5G是第五代移动通信技术，5G网络理论下载速度可以达到每秒130000KB以上，用科学记数法表示130000是（ ）
A．13×105B．1.3×105C．1.3×106D．1.3×107
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：130000＝1.3×105，
故选：B．
2．（3分）无论x取何值，下列式子的值一定是正数的是（ ）
A．|x|B．|x2|C．|x+1|D．x2+1
【分析】讨论每个选项后，作出判断．注意平方数和绝对值都可是非负数．
【解答】解：A．|x|≥0，此选项不符合题意；
B．|x2|≥0，此选项不符合题意；
C．|x+1|≥0，此选项不符合题意；
D．x2+1≥1＞0，此选项符合题意；
故选：D．
3．（3分）下列各组中，不是同类项的是（ ）
A．52与25B．﹣ab与ba
C．0.2a2b与﹣a2bD．a2b3与﹣a3b2
【分析】利用同类项的定义判断即可．
【解答】解：不是同类项的是a2b3与﹣a3b2．
故选：D．
4．（3分）如图，数轴上的点M，P，N，Q分别表示四个有理数，若点M，N表示的有理数互为相反数，则图中表示正数的点的个数是（ ）
A．1B．2C．3D．4
【分析】先利用相反数的定义确定原点为线段MN的中点，则可判定点Q到原点的距离最大，然后根据绝对值的定义可判定点Q表示的数的绝对值最大．
【解答】解：点M，N表示的有理数互为相反数，
∴原点O在M、N的中点处，
∴图中在原点O右边为正数的点是P、N、Q三个点．
故选：C．
5．（3分）设想有一根铁丝套在地球的赤道上，刚好拉紧后，又放长了10米，并使得铁丝均匀地离开地面．则下面说法中比较合理的是（ ）
A．你只能塞过一张纸B．只能伸进你的拳头
C．能钻过一只小羊D．能驶过一艘万吨巨轮
【分析】设地球赤道处的半径为R，铁丝均匀地离开地面的高度是h，利用圆的周长公式计算出高度h，然后进行选择．
【解答】解：设地球的半径是R，铁丝均匀地离开地面的高度是h，由圆的周长公式有：
2π（R+h）＝2πR+10
2πR+2πh＝2πR+10
∴2πh＝10
h＝≈1.6米．
根据纸的厚度，进行分析，应选：C．
故选：C．
6．（3分）如图，一枚棋子放在七角棋盘的第0号角，现依逆时针方向移动这枚棋子，其各步依次移动1，2，3，…，n个角，如第一步从0号角移动到第1号角，第二步从第1号角移动到第3号角，第三步从第3号角移动到第6号角，…．若这枚棋子不停地移动下去，则这枚棋子永远不能到达的角的个数是（ ）
A．0B．1C．2D．3
【分析】因棋子移动了k次后走过的总格数是1+2+3+…+k＝k（k+1），然后根据题目中所给的第k次依次移动k个顶点的规则，可得到不等式最后求得解．
【解答】解：因棋子移动了k次后走过的总格数是1+2+3+…+k＝k（k+1），应停在第k（k+1）﹣7p格，
这时P是整数，且使0≤k（k+1）﹣7p≤6，分别取k＝1，2，3，4，5，6，7时，
k（k+1）﹣7p＝1，3，6，3，1，0，0，发现第2，4，5格没有停棋，
若7＜k≤10，设k＝7+t（t＝1，2，3）代入可得，k（k+1）﹣7p＝7m+t（t+1），
由此可知，停棋的情形与k＝t时相同，
故第2，4，5格没有停棋，
即：这枚棋子永远不能到达的角的个数是3．
故选：D．
二、填空题（本大题共10小题，每小题3分，共20分.）
7．（3分）﹣2的相反数是 2 ．
【分析】根据一个数的相反数就是在这个数前面添上“﹣”号，求解即可．
【解答】解：﹣2的相反数是：﹣（﹣2）＝2，
故答案为：2．
8．（3分）单项式﹣3x2的系数是 ﹣3 ．
【分析】利用单项式系数定义可得答案．
【解答】解：单项式﹣3x2的系数是﹣3，
故答案为：﹣3．
9．（3分）比较大小：﹣ ＜ ﹣．
【分析】根据负有理数比较大小的方法比较（绝对值大的反而小）．
【解答】解：根据两个负数，绝对值大的反而小的规律得出：﹣＜﹣．
10．（3分）点A表示数轴上的一个点，将点A向右移动5个单位，再向左移动4个单位，终点恰好是原点，则点A表示的数是 ﹣1 ．
【分析】由原点向右移动4个单位，再向左移动5个单位，即可得出点A的坐标．
【解答】解：0+4﹣5＝﹣1．
故点A表示的数是﹣1．
故答案为：﹣1．
11．（3分）若|a|＝6，b＝4，且a+b＜0，那么a﹣b＝ ﹣10 ．
【分析】根据条件求出a，b的值，再求a﹣b的值即可．
【解答】解：∵|a|＝6，
∴a＝±6，
∵a+b＜0，
∴a＝﹣6，
∴a﹣b＝﹣6﹣4＝﹣6+（﹣4）＝﹣10，
故答案为：﹣10．
12．（3分）观察下面的单项式：x，﹣2x2，4x3，﹣8x4，…．根据你发现的规律，写出第7个式子是 64x7 ．
【分析】主要看各单项式的系数和次数与该项的序号之间的变化规律．本题中，奇数项符号为正，数字变化规律是2n﹣1，字母变化规律是xn．
【解答】解：各单项式的系数依次是1，﹣2，4，﹣8，…；次数依次是1，2，3，4…；可以推出第七个式子的系数应该是64，次数是7，即64x7．
13．（3分）多项式x|m|﹣（m﹣2）x+7是关于x的二次三项式，则m＝ ﹣2 ．
【分析】根据二次三项式的定义可得：|m|＝2，且m﹣2≠0，再解即可．
【解答】解：由题意得：|m|＝2，且m﹣2≠0，
解得：m＝﹣2，
故答案为：﹣2．
14．（3分）若a2﹣3b＝5，则6b﹣2a2+2021＝ 2011 ．
【分析】将代数式适当变形，利用整体代入的方法解答即可．
【解答】解：∵a2﹣3b＝5，
∴6b﹣2a2+2021
＝﹣2（a2﹣3b）+2021
＝﹣2×5+2021
＝﹣10+2021
＝2011．
故答案为：2011．
15．（3分）有一数值转换器，原理如图所示，若开始输入x的值是7，可以得出第1次输出的结果是12，第2次输出的结果是6，依次继续下去…，第2021次输出的结果是 4 ．
【分析】根据题意可以先求出前几次输出结果，发现规律：从第2次开始，6，3，8，4，2，1，每次6个数循环，进而可得以第2021次输出的结果与第5次输出的结果一样．
【解答】解：根据题意可知：
开始输入x的值是7，第1次输出的结果是12，
第2次输出的结果是6，
第3次输出的结果是3，
第4次输出的结果是8，
第5次输出的结果是4，
第6次输出的结果是2，
第7次输出的结果是1，
第8次输出的结果是6，
依次继续下去，
…，
发现规律：从第2次开始，6，3，8，4，2，1，每次6个数循环，
因为（2021﹣1）÷6＝336…4，
所以第2021次输出的结果与第5次输出的结果一样是4．
故答案为：4．
16．（3分）在一列数：a1，a2，a3，…，an中，a1＝2，a2＝，a3＝4，且任意相邻的三个数的积都相等．若前n个数的积等于64，则n＝ 18或16或23 ．
【分析】根据数字的变化规律每三个数为一组，寻找规律式即可求解．
【解答】解：由任意相邻的三个数的积都相等．可知：
a4＝2，a5＝，a6＝4，…，
可得：a1，a4，a7，…，a3n﹣2，相等为2，
a2，a5，a8，…，a3n﹣1，相等为，
a3，a6，a9，…，a3n，相等为4，
∵相邻的三个数的积为2，∴将这列数每3个分成一组，
∵64＝26，可知6组数之积为64，则n＝18，满足题意；
由规律，得a16＝2，a17＝，a18＝4，a17•a18＝1，
∴前16个数之积为64，则n＝16满足题意；
由规律，得a19＝2，a20＝，a21＝4，a22＝2，•a23＝，
它们五个数相乘为1，所以前23个数之积为64．则n＝23满足题意．
故答案为18或16或23．
三、解答题（本大题共9小题，共68分.）
17．（4分）将下列各数填在相应的集合里﹣|﹣2.5|、0、﹣（﹣52）、、−1.2121121112、、π．
正数集合：{ ﹣（﹣52），+（﹣）2，π …}；
整数集合：{ 0，﹣（﹣52） …}；
负分数集合：{ ﹣|﹣2.5|，﹣1.2121121112，﹣ …}；
无理数集合：{ π …}．
【分析】先根据绝对值的定义及化简符号的法则去掉绝对值的符号及多重符号，再根据正数、整数、负分数、无理数的定义求解即可．
【解答】解：﹣|﹣2.5|＝﹣2.5，﹣（﹣52）＝25，+（﹣）2＝．
正数集合：{﹣（﹣52），+（﹣）2，π…}；
整数集合：{0，﹣（﹣52）…}；
负分数集合：{﹣|﹣2.5|，﹣1.2121121112，﹣…}；
无理数集合：{π…}．
故答案为：﹣（﹣52），+（﹣）2，π；0，﹣（﹣52）；﹣|﹣2.5|，﹣1.2121121112，﹣；π．
18．（12分）计算：
（1）．
（2）．
（3）．
【分析】（1）先算乘法，整数加法；
（2）先算小括号里面的加减法，再算括号外面的除法；
（3）先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有绝对值，要先做绝对值内的运算．
【解答】解：（1）
＝﹣1﹣2
＝﹣3；
（2）
＝（﹣+）×（﹣）
＝×（﹣）
＝﹣；
（3）
＝﹣9﹣6+1+4×2
＝﹣9﹣6+1+8
＝﹣6．
19．（5分）先化简，再求值：x﹣2（）+（﹣），其中x＝，y＝﹣2．
【分析】原式去括号合并得到最简结果，把x与y的值代入计算即可求出值．
【解答】解：原式＝x﹣x+y2﹣x+y2＝﹣x+y2，
当x＝，y＝﹣2时，原式＝2.5．
20．（8分）已知四个数，a＝﹣22，b＝﹣|﹣2|，c＝﹣（﹣1）100，d＝﹣（﹣3）．
（1）计算a、b、c、d，得a＝ ﹣4 ，b＝ ﹣2 ，c＝ ﹣1 ，d＝ 3 ；
（2）把这四个数在如图所示的数轴上分别表示出来．
（3）用“＜”把a、b、c、d连接起来．
（4）用“＞”把|a|、|b|、|c|、|d|连接起来．
【分析】（1）根据有理数的乘方，绝对值，相反数求出答案即可；
（2）把各个数在数轴上表示出来即可；
（3）根据有理数的大小比较法则比较即可；
（4）求出绝对值，再根据实数的大小比较法则比较即可．
【解答】解：（1）a＝﹣22＝﹣4，b＝﹣|﹣2|＝﹣2，c＝﹣（﹣1）100＝﹣1，d＝﹣（﹣3）＝3，
故答案为：﹣4，﹣2，﹣1，3；
（2）在数轴上表示为：
；
（3）∵a＝﹣4，b＝﹣2，c＝﹣1，d＝3，
∴a＜b＜c＜d；
（4）|a|＝|﹣4|＝4，|b|＝|﹣2|＝2，|c|＝|﹣1|＝1，|d|＝|3|＝3，
∴|a|＞|d|＞|b|＞|c|．
21．（8分）定义一种新运算：观察下列式：
1⊙3＝1×4+3＝7
3⊙（﹣1）＝3×4﹣1＝11
5⊙4＝5×4+4＝24
4⊙（﹣3）＝4×4﹣3＝13
（1）请你想一想：a⊙b＝ 4a+b ；
（2）若a≠b，那么a⊙b ≠ b⊙a（填入“＝”或“≠”）
（3）若a⊙（﹣2b）＝4，请计算（a﹣b）⊙（2a+b）的值．
【分析】（1）根据提供的信息，⊙的运算法则是⊙前面的数乘以4再加上运算符号后面的数，然后写出即可；
（2）根据运算规则把a⊙b和b⊙a分别进行计算并相减得到a、b的差，然后即可比较大小；
（3）先根据运算规则与已知条件求出a、b的关系，然后再根据运算规则计算（a﹣b）⊙（2a+b）并把a、b的关系代入整理后的算式计算即可求解．
【解答】解：（1）∵1⊙3＝1×4+3＝7，3⊙（﹣1）＝3×4﹣1＝11，5⊙4＝5×4+4＝24，4⊙（﹣3）＝4×4﹣3＝13，
∴a⊙b＝4a+b；
（2）a⊙b＝4a+b，b⊙a＝4b+a，
（4a+b）﹣（4b+a）＝3a﹣3b＝3（a﹣b），
∵a≠b，
∴3（a﹣b）≠0，
即（4a+b）﹣（4b+a）≠0，
∴a⊙b≠b⊙a；
（3）∵a⊙（﹣2b）＝4a﹣2b＝4，
∴2a﹣b＝2，
（a﹣b）⊙（2a+b）
＝4（a﹣b）+（2a+b）
＝4a﹣4b+2a+b，
＝6a﹣3b，
＝3（2a﹣b）
＝3×2
＝6．
故答案为：（1）4a+b，（2）≠，（3）6．
22．（8分）已知M＝4x2﹣2x﹣1，N＝3x2﹣2x﹣5．
（1）当x＝﹣1时，求代数式4M﹣（2M+3N）的值；
（2）试判断M、N的大小关系，并说明理由．
【分析】（1）先将代数式去括号化简，然后再将M和N代入，去括号，合并同类项进行化简，最后代入求值；
（2）利用作差法并结合偶次幂的非负性进行分析判断．
【解答】解：（1）4M﹣（2M+3N）
＝4M﹣2M﹣3N
＝2M﹣3N，
∵M＝4x2﹣2x﹣1，N＝3x2﹣2x﹣5，
∴原式＝2（4x2﹣2x﹣1）﹣3（3x2﹣2x﹣5）
＝8x2﹣4x﹣2﹣9x2+6x+15
＝﹣x2+2x+13，
当x＝﹣1时，
原式＝﹣（﹣1）2+2×（﹣1）+13
＝﹣1﹣2+13
＝10；
（2）M﹣N＝（4x2﹣2x﹣1）﹣（3x2﹣2x﹣5）
＝4x2﹣2x﹣1﹣3x2+2x+5
＝x2+4，
∵无论x为何值，x2≥0，
∴x2+4≥4，
∴M＞N．
23．（8分）运动会前夕，为了提高体能，小明每天放学回家做仰卧起坐．他制作了一张表格记录自己每天做仰卧起坐的成绩．以每分钟做40个为标准，超过的个数记为正，不足的个数记为负．下表是小明一周做仰卧起坐的记录：
根据上述记录表，回答下列问题：
（1）小明这周一天最多做 54 个，最少做 30 个；
（2）这周小明平均每天做多少个？
【分析】（1）正数最大是“+14”，所以可用40+14进行计算，所得结果即为做得最多的个数，负数最小是“﹣10”，所以可用40﹣10进行计算，所得结果即为做得最少的个数；
（2）先求出表格中7个数的平均数，再加上40即可．
【解答】解：（1）做得最多的是：40+14＝54，
做得最少的是：40﹣10＝30．
故答案为54，30；
（2）（14+8﹣5+2﹣10+1﹣3）÷7+40＝1+40＝41，
答：这周小明平均每天做41个．
24．（7分）生活与数学：
（1）吉姆同学在某月的日历上圈出2×2个数，正方形的方框内的四个数的和是32，那么第一个数是 4 ；
（2）玛丽也在日历上圈出2×2个数，斜框内的四个数的和是42，则它们分别是 7，8，13，14 ；
（3）莉莉也在日历上圈出5个数，呈十字框形，它们的和是50，则中间的数是 10 ；
（4）某月有5个星期日的和是75，则这个月中最后一个星期日是 29 号；
（5）若干个偶数按每行8个数排成图4：
①图中方框内的9个数的和与中间的数有什么关系： 9个数的和是中间的数的9倍 ；
②汤姆所画的斜框内9个数的和为360，则斜框的中间一个数是 40 ；
③托马斯也画了一个斜框，斜框内9个数的和为252，则斜框的中间一个数是 28 ．
【分析】（1）先根据日历上的数据规律，设第一个数是x，其他的数为x+1，x+7，x+8，用一元一次方程求解即可；
（2）根据日历上的数据规律，设第一个数是x，其他的数为x+1，x+6，x+7，用一元一次方程求解即可；
（3）根据日历上的数据规律，设中间的数是x，根据5个数的和是50列方程即可；
（4）根据日历上的数据规律，设最后一个星期日是x，则其他的星期日为x﹣7，x﹣14，x﹣21，x﹣28，用一元一次方程求解即可；
（5）①通过计算可以得出结论；
②根据①的规律，设中间的数是x，列方程求解即可；
③根据①的规律，设中间的数是x，列方程求解即可．
【解答】解：（1）设第一个数是x，其他的数为x+1，x+7，x+8，
则x+x+1+x+7+x+8＝32，
解得x＝4，
故答案为：4；
（2）设第一个数是x，其他的数为x+1，x+6，x+7，
则x+x+1+x+6+x+7＝42，
解得x＝7，
则x+1＝8，x+6＝13，x+7＝14，
故答案为：7，8，13，14；
（3）设中间的数是x，
则5x＝50，
解得x＝10，
故答案为：10；
（4）设最后一个星期日是x，则其他的星期日为x﹣7，x﹣14，x﹣21，x﹣28，
则x+x﹣7+x﹣14+x﹣21+x﹣28＝75，
解得x＝29，
故答案为：29；
（5）①2+4+6+18+20+22+34+36+38＝180＝9×20，
故答案为：9个数的和是中间的数的9倍；
②根据规律可知，和是中间的数的9倍，
设中间的数是x，
则9x＝360，
解得x＝40，
故答案为：40；
③设中间的数是x，
则9x＝252，
解得x＝28，
故答案为：28．
25．（8分）阅读下面材料：
点A、B在数轴上分别表示数a、b．A、B两点之间的距离表示为|AB|．则数轴上A、B两点之间的距离|AB|＝|a﹣b|．
回答下列问题：
（1）数轴上表示1和﹣3的两点之间的距离是 4 ；数轴上表示﹣2和﹣5的两点之间的距离是 3 ；
（2）数轴上表示x和﹣1的两点A和B之间的距离是 |x+1| ，如果|AB|＝2，那么x为 1或﹣3 ；
（3）当|x+1|+|x﹣2|取最小值时，符合条件的整数x有 ﹣1，0，1，2 ；
（4）令y＝|x+1|+|x﹣2|+|x﹣3|，问当x取何值时，y最小，最小值为多少？请求解．
【分析】（1）根据两点间的距离的求解列式计算即可得解；
（2）根据两点之间的距离表示列式并计算即可；
（3）根据数轴上两点间的距离的意义解答；
（4）根据数轴上两点间的距离的意义解答．
【解答】解：（1）数轴上表示1和﹣3的两点之间的距离是：1﹣（﹣3）＝1+3＝4；
数轴上表示﹣2和﹣5的两点之间的距离是：﹣2﹣（﹣5）＝﹣2+5＝3；
故答案为：4；3；
（2）∵A，B分别表示的数为x，﹣1，
∴数轴上表示x和﹣1的两点A和B之间的距离是|x+1|，
如果|AB|＝2，则|x+1|＝2，
解得x＝1或﹣3；
故答案为：|x+1|；1或﹣3；
（3）当|x+1|+|x﹣2|取最小值时，﹣1≤x≤2，
∴符合条件的整数x有﹣1，0，1，2．
故答案为：﹣1，0，1，2；
（4）当|x+1|+|x﹣2|+|x﹣3|取最小值时，x＝2，
∴当x＝2时，y最小，
即最小值为：|2+1|+|2﹣2|+|2﹣3|＝4．
故x＝2时，y最小，最小值为4．
时间
星期一
星期二
星期三
星期四
星期五
星期六
星期日
个数
+14
+8
﹣5
+2
﹣10
+1
﹣3
时间
星期一
星期二
星期三
星期四
星期五
星期六
星期日
个数
+14
+8
﹣5
+2
﹣10
+1
﹣3